이번 포스팅에서는 주성분 분석(Principal Component Analysis : PCA)에 대한 개념과 파이썬(Python)을 이용하여 구현하는 방법에 대해서 알아본다.
- 목차 -
주성분 분석을 이해하기 위해선 고유값 분해와 특이값 분해에 대한 내용을 알아야 한다. 아래 포스팅에 해당 내용을 정리했으니 참고하면 된다.
고유값과 고유 벡터 그리고 고유값 분해(Eigen Decomposition)에 대해서 알아보자 (feat. Numpy)
고유값과 고유 벡터 그리고 고유값 분해(Eigen Decomposition)에 대해서 알아보자 (feat. Numpy)
이번 포스팅에서는 고유값과 고유 벡터에 대해서 간단히 알아본 뒤 고유값 분해(Eigen Decomposition)에 대해서 알아보고자 한다. 고유값 분해(Eigen Decomposition) 고유값 분해를 이야기하기 전에 간단하
zephyrus1111.tistory.com
특이값 분해(Singular Value Decomposition : SVD)에 대해서 알아보자(feat. Numpy)
특이값 분해(Singular Value Decomposition : SVD)에 대해서 알아보자(feat. Numpy)
이번 포스팅에서는 고유값 분해(Eigen Decomposition)의 일반화 버전인 특이값 분해(Singular Value Decomposition : SVD)에 대한 내용을 정리해 보았다. SVD의 개념과 Numpy 모듈을 이용하여 SVD 표현식을 구하는
zephyrus1111.tistory.com
1. 주성분 분석이란?
1) 정의
주성분 분석은 데이터의 분산 구조를 잘 설명하는 축을 구하는 과정을 말한다. 필요에 따라서 축의 일부만을 예측 모형 학습에 사용함으로써 차원 축소 효과를 얻을 수 있다.
2) 파헤치기
앞에서 소개한 주성분 분석의 정의를 하나하나 파헤쳐보자.
a. 데이터의 분산 구조
데이터 $x_i = (x_{i1}, x_{i2}, \ldots, x_{ip})^t, i=1, \ldots, n$이 있다고 하자. 즉, 데이터 개수는 $n$개 변수의 개수는 $p$개이다. $x_i$를 $i$ 번째 행으로 갖는 $n\times p$ 행렬을 $X$라 하자. 즉, $x_i$는 $X$의 행벡터인 것이다. 이번엔 $X$의 $j$번째 칼럼을 $x_j = (x_{1j}, x_{2j}, \ldots, x_{nj})^t$라 하자. 모든 $j$에 대하여 $j$ 번째 칼럼에 $j$ 번째 평균 $\bar{x}_j = \sum_{i=1}^nx_{ij}/n$를 빼준다(이를 Mean Centering 이라 한다). 후술 하는 $x_j$는 평균을 빼준 것으로 가정하겠다.
서두가 길었다. 각 칼럼별로 평균을 빼주었으므로 $X$의 표본 분산 행렬은 다음과 같다.
$$\text{Var}(X) = \frac{1}{n-1}X^tX \tag{1.1}$$
이때 각 변수의 (표본) 분산 총합은 (1.1)에서 대각 원소들의 합이다. 즉,
$$\text{Total Sum of Variance} = \text{tr}(\text{Var}(X)) \tag{1.2}$$
주성분 분석을 이야기할 때 나오게 되는 데이터의 분산 구조는 (1.2)를 말하는 것이다.
b. 데이터의 분산 구조를 잘 설명하는 축을 구하는 과정이 PCA이다.
먼저 2차원 데이터가 다음과 같이 분포되어 있다고 해보자. 이때 빨간 점은 평균을 나타낸다.
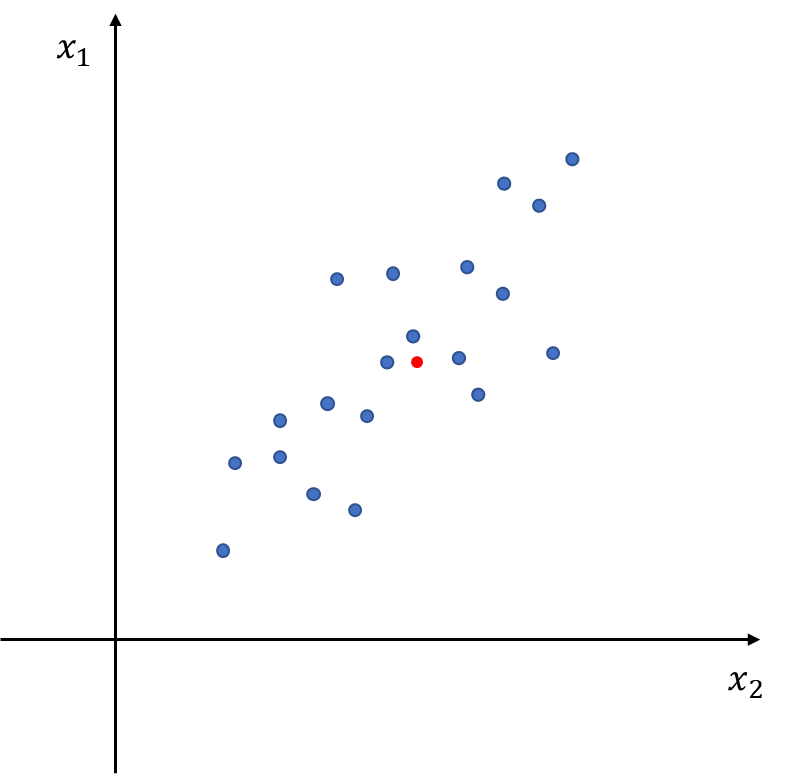
이제 평균을 지나는 직선 중에서 어떤 직선이 데이터를 잘 설명하는 것일까?


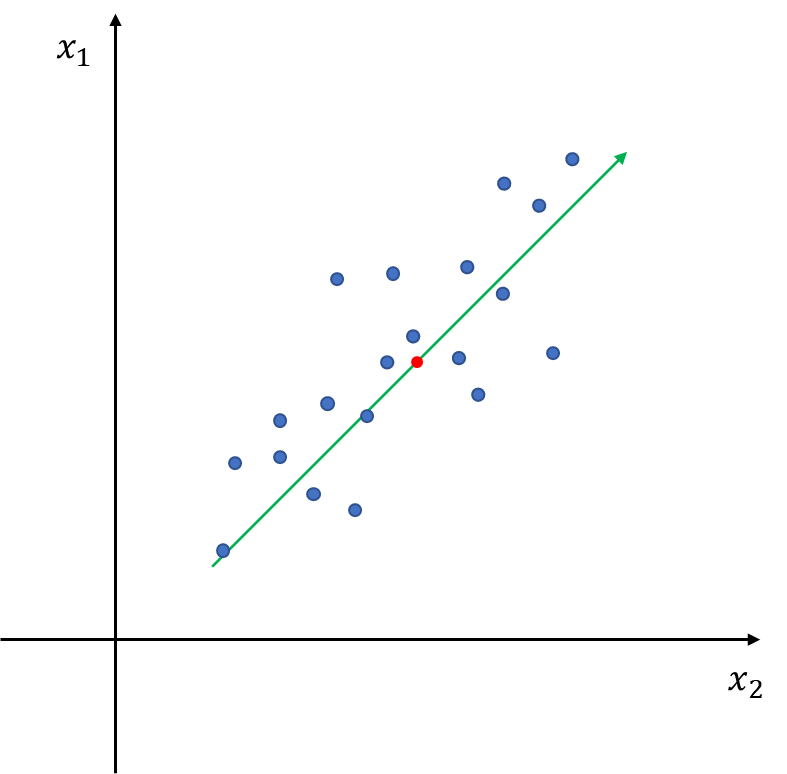
바로 세 번째 직선이 데이터를 잘 설명하는 것이다. 여기서 데이터를 잘 설명하는 직선의 의미는 데이터와 데이터를 해당 직선 위의 정사영 벡터 간 차이를 최소화하는 직선을 말한다(아래 그림에서 검은색 양방향 화살표).
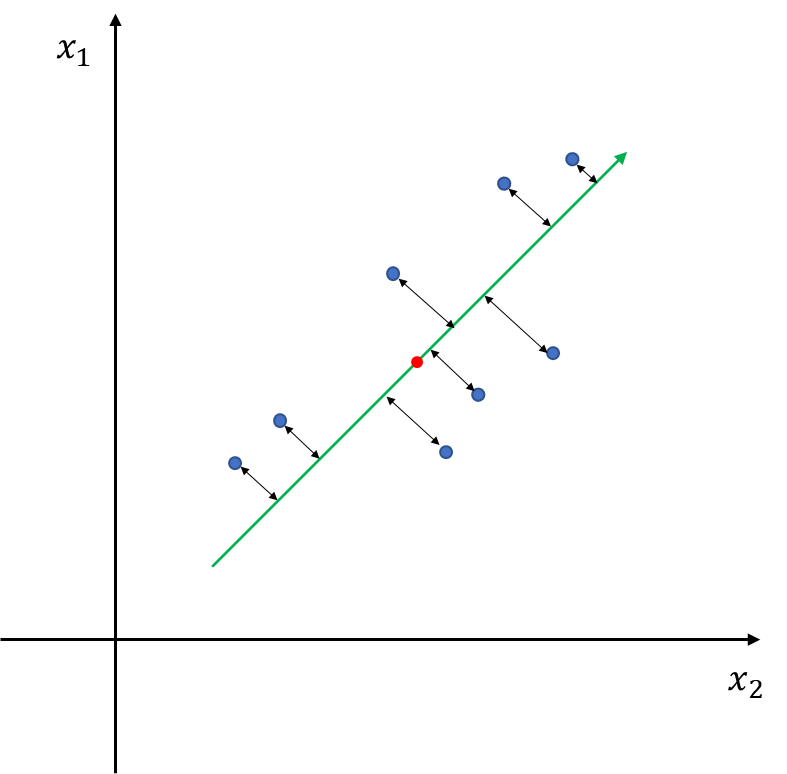
이를 좀 더 일반화하면 길이가 1인 벡터 $v$ 중에서 데이터와 그 데이터에 대한 $v$위의 정사영 벡터 간의 차이를 최소화하는 것이다. 이를 수식으로 표현하면 다음과 같다.
$$\DeclareMathOperator*{\argminA}{arg\,min} \argminA_{v : \|v\|_2 = 1} \sum_{i=1}^n\| x_i - (x_i^tv)v \|_2^2 \tag{1.3}$$
여기서 $\| x \|_2^2 = \sum_{j=1}^px_j^2$이다.
지금까지의 설명은 일종의 잔차를 최소화하는 축을 찾은 것인데 이것이 데이터 분산 구조를 설명하는 것과 무슨 관련이 있을까?
(1.3)을 다시 쓰면 다음과 같다.
$$\DeclareMathOperator*{\argminA}{arg\,min} \begin{align} \argminA_{v : \|v\|_2 = 1} \sum_{i=1}^n \left ( x_i -(x_i^tv)v\right )^t \left ( x_i -(x_i^tv)v \right ) &= \argminA_{v : \|v\|_2 = 1} \sum_{i=1}^n \left ( x_i^tx_i -(x_i^tv)^2\right ) \\ &= \DeclareMathOperator*{\argmax}{arg\,max} \argmax_{v : \|v\|_2 = 1} \sum_{i=1}^n(x_i^tv)^2 \\ &= \argmax_{v : \|v\|_2 = 1} \|Xv \|_2^2 \\ &= \argmax_{v : \|v \|_2=1} v^tX^tXv \\ &= \argmax_{v: \|v \|_2 = 1} v^t \text{Var}(X) v \end{align} \tag{1.4} $$
여기서
$$\text{Var}(X) = \frac{1}{n-1}X^tX$$
이다. 이때 두 번째 등식에서
$$\sum_{i=1}^n(x_i^tv)^2\tag{1.5}$$
이 부분의 의미는 데이터를 $v$ 위로 투영시켰을 때 생기는 정사영의 길이의 제곱이다($\|v\|_2=1$이기 때문에 내적이 곧 정사영의 길이가 된다). 이때 데이터는 평균 벡터를 빼준 상황이므로 $v$위로 투영시켰을 때 생기는 새로운 데이터들의 분산과 관련되는 것이다(앞에 상수 $1/(n-1)$이 있어야 하나 최적화 문제에서는 빠져도 된다). 다시 말해 (1.5)는 아래 그림에서 데이터를 초록색 직선에 투영시키고 얻은 새로운 데이터를 파란 화살표라고 할 때 이 화살표 길이의 분산을 최대화하는 직선을 찾는 것과 동일하다는 것이다.
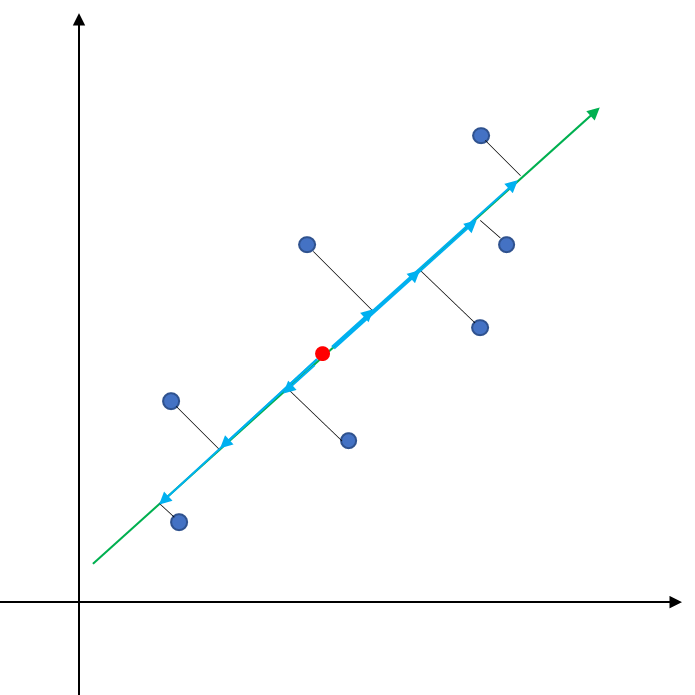
즉, (1.3)은 정사영들의 분산을 최대화하는 직선을 찾는 문제와 같아지는 것이다. 이러한 직선(또는 축)을 찾는 과정이 바로 PCA이다.
하지만 정사영들의 분산을 최대화하는 것과 데이터 총분산 (1.2)와의 연결고리를 아직 설명할 수 없다. 이는 다음 섹션에서 자세하게 설명한다.
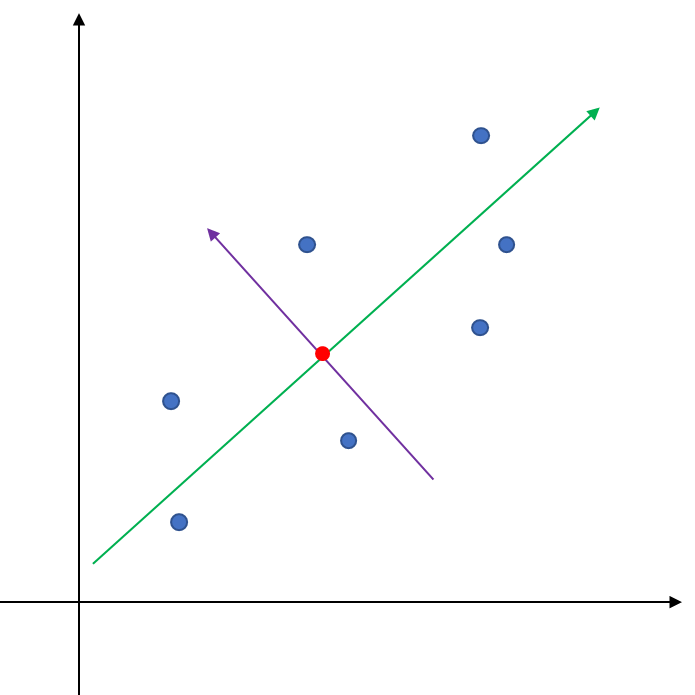
이러한 직선(또는 축)은 하나만 찾는 것이 아니며 이론적으로 $x_i$의 차원만큼의 축을 찾을 수 있다. 만약 아래 그림과 같이 정사영의 분산을 최대화하는 초록색 축을 찾았다면 이 축과 수직을 이루고 평균 벡터를 지나는 직선 중에서 정사영의 분산을 최대화하는 다음 축을 찾는다. 다음 축을 기존 축과 수직인 것들 중에서 찾는 이유는 일반적으로 두 축이 수직을 이루기 때문이다. 2차원 데이터에 대해서는 하나의 축을 찾았다면 나머지 하나의 축은 기존 축과 수직이면서 평균 벡터를 지나는 직선으로 바로 결정된다(아래 그림에서 보라색 화살표).
2. 주성분 분석 과정
1) 주성분 구하기
주성분 분석의 개념을 알았으니 주성분을 실제로 구하는 과정을 선형 대수와 관련된 정리를 이용하여 알아보자. 먼저 주성분을 구하는 과정에서 핵심이 되는 정리를 하나 소개한다.
정리 2.1 (고유값 분해)
$A$가 $n \times n$ 대칭 행렬인 경우 $n \times n$ Orthonormal 행렬 $Q$와 $A$의 고유값을 대각 원소로 하는 대각 행렬 $\Lambda$에 대하여 $A$를 다음과 같이 쓸 수 있다.
$$A = Q\Lambda Q^t$$
데이터로 이루어진 $n \times p$ 행렬 $X$에 대하여 $\text{Var}(X)$는 대칭 행렬이다. 따라서 정리 2.1에 의하여 $p \times p$ Orthonormal 행렬 $Q$와 $\text{Var}(X)$의 고유값을 대각 원소로하는 대각 행렬 $\Lambda$에 대하여 $\text{Var}(X)$를 다음과 같이 쓸 수 있다.
$$ \text{Var}(X) = Q\Lambda Q^t \tag{2.1}$$
$\text{Var}(X)$의 고유값을 내림차순으로 정렬한 것이 $\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_p$이라하고 $i$번째 대각원소 $\Lambda_{i, i} = \lambda_i$이다. 그리고 $\lambda_i$에 대응하는 고유 벡터는 $Q$의 $i$번째 칼럼 벡터 $q_i$이다.
이때 (1.4)를 최대화하는 벡터 $v=q_1$이 되며 그 값은
$$q_1^t \text{Var}(X)q_1 = \lambda_1 \tag{2.2} $$
이다.
(2.2) 증명
$\| v\|_2 = 1$인 모든 $v$에 대하여
$$\begin{align} v^t \text{Var}(X)v &= v^tQ\Lambda Q^t v \\ &= w^t \Lambda w \\ &= \sum_{j=1}^p\lambda_j w_j^2 \\ & \leq \lambda_1 \sum_{j=1}^p w_j^2 = \lambda_1 \end{align}$$
여기서 $w = Q^tv$이며 맨 마지막 등식은
$$\sum_{j=1}^p w_j^2 = w^tw = v^tQ^tQv = v^tv = 1$$
임을 이용했다.
(1.4)의 상한이 $\text{Var}(X)$의 가장 큰 고유값 $\lambda_1$임을 보였고 그 상한을 달성하는 벡터가 $q_1$임을 보이면 증명은 끝난다.
$$\begin{align} q_1^tX^tXq_1 &= q_1^tQ\Lambda Q^t q_1 \\ &= e_1^t \Lambda e_1 \\ &= \lambda_1 \end{align}$$
여기서 $e_1$은 첫 번째 원소만 1이고 나머지는 0인 $p$차원 벡터이다. 그리고 $q_1Q = e_1$인 것은 $q_1^tq_1 = 1$이고 $q_1$이 $q_2, \ldots, q_p$와 수직(Orthogonal)이기 때문이다.
(1.4)를 최대화하는 첫 번째 축은 $q_1$임을 보였다. 이제 $q_1$과 수직인 단위 벡터 중에서 (1.4)를 최대화하는 것은 $\text{Var}(X)$의 두 번째로 큰 고유값 $\lambda_2$에 대응하는 고유 벡터 $q_2$이며 그 값은 $\lambda_2$이다. 즉,
$$\DeclareMathOperator*{\argmax}{arg\,max} \argmax_{v \in \{v : v \perp q_1, \|v\|_2 = 1 \}} v^t\text{Var}(X)v = q_2, \\ q_2\text{Var}(X)q_2 = \lambda_2 \tag{2.3}$$
(2.3) 증명
$p \times p$ 대칭 행렬의 고유 벡터는 서로 수직이라는 사실이 알려져 있다. $\text{Var}(X)$의 고유 벡터 $q_1, q_2, \ldots, q_p$는 수직이며 그에 따라 선형 독립이 된다. 또한 각 고유 벡터는 $p$차원이므로 $q_1, q_2, \ldots, q_p$는 $\mathbb{R}^p$ 벡터 공간에서 기저 함수(Basis)가 된다.
$v \perp q_1$이고 $\| v\|_2$인 $v$에 대하여 $v$도 $p$차원 벡터이므로 다음과 같이 쓸 수 있다.
$$v = a_1q_1+a_2q_2 + \cdots + a_pq_p$$
이때 $v \perp q_1$이므로
$$v^tq_1 = a_1q_1^t q_1 + a_2q_2^tq_1+ \cdots a_pq_p^t q_1 = a_1q_1^tq_1 = a_1 = 0$$
이다. 또한 $\| v\|_2=1$이므로
$$1 = \|v \|_2^2 = v^tv = \sum_{j=2}^p a_j^2$$
임을 알 수 있다.
(2.2) 증명에서와 비슷한 방법으로
$$\begin{align}v^t\text{Var}(X)v &= v^tQ\Lambda Q^t v \\ &= w^t \Lambda w \\ &= \sum_{j=2}^p \lambda_j a_j^2 \\ & \leq \lambda_2 \sum_{j=2}^p a_j^2 = \lambda_2 \end{align}$$
여기서 $w = Q^tv = (0, a_2, \ldots, a_p)^t$이다. 그리고
$$q_2^2 \text{Var}(X)q_2 = \lambda_2$$
임을 쉽게 알 수 있다.
(2.2)와 (2.3)의 과정을 반복하면 우리는 $q_1, \ldots, q_p$ 까지의 축을 구할 수 있다는 것을 알 수 있다. 이때 $q_j$를 $j$번째 성분이라 하며 $Xq_j$를 $j$번째 주성분이라 한다. 주성분의 기하학적인 해석을 위하여 다음과 같이 써보자.
$$\begin{align}T &= XQ = X(q_1 q_2 \cdots q_p) \\ &= (Xq_1 Xq_2 \cdots Xq_p) \end{align} \tag{2.4}$$
(2.4)에서 $Xq_j$는 $n$개의 데이터 $x_i = (x_{i1}, \ldots, x_{ip})^t$를 $q_j$로 투영시켜 얻은 정사영들의 벡터임을 감안하면 $XQ$는 표준 기저함수(Standard Basis)로 표현된 데이터를 $\text{Var}(X)$의 고유 벡터로 구성된 새로운 기저함수 $q_1, \ldots, q_p$으로 표현한 것임을 알 수 있다.
따라서 $j$번째 주성분 $Xq_j$는 $j$번째 성분에 대한 좌표가 된다.
지금까지의 내용을 토대로 알 수 있는 것은 주성분을 구하기 위해선 $\text{Var}(X)$의 고유값을 내림차순으로 정렬한 뒤 각 고유값에 대응하는 고유 벡터를 차례대로 구하면 주성분을 구할 수 있다는 것이다.
2) 성질
주성분의 대한 몇 가지 성질을 알아보자.
$j$번째 주성분을 $PC_j$라 할 때 다음이 성립한다.
$$ \sum_{j=1}^p\text{Var}(x_j) = \text{tr}(\text{Var}(X)) = \sum_{j=1}^p\lambda_j \tag{2.4}$$
$$ \text{Var}(PC_j) = \text{Var}(Xq_j) = q_j^t \text{Var}(X) q_j = \lambda_j \tag{2.5}$$
$$\text{Cov}(PC_j, PC_k) = \text{Cov}(Xq_j, Xq_k) = q_j^tVar(X)q_k = \lambda_k q_j^tq_k = 0 \tag{2.6}$$
(2.4)에서는 정방행렬의 trace는 고유값의 합과 같다는 사실을 이용했다.
(2.4)와 (2.5)를 통해 주성분 분산의 합과 데이터의 총 분산이 같다는 것을 알 수 있으며 (2.5)와 (2.6)을 통해 각 주성분은 독립적으로 데이터의 총 분산을 설명한다고 볼 수 있는 것이다.
또한 고유값을 내림차순으로 정했으므로 첫 번째 주성분이 데이터의 총분산을 가장 잘 설명하는 것을 알 수 있으며 $j$번째 주성분이 데이터의 총 분산을 설명하는 정도를 아래와 같이 비율로 정의할 수 있다.
$$\frac{\lambda_j}{\text{tr}(\text{Cov}(X))}$$
첫 번째 주성분부터 $j$ 번째 주성분까지의 데이터 총 분산의 누적 설명 비율도 정의할 수 있다.
$$\frac{\sum_{l=1}^j\lambda_l}{\text{tr}(\text{Cov}(X))}$$
이번엔 $j$ 번째 주성분 $PC_j = Xq_j$와 $k$번째 설명 변수 벡터 $x_k = (x_{1k}, x_{2k}, \ldots, x_{nk})^t$의 상관 계수를 살펴보자.
$$\begin{align} \rho (x_k, PC_j) &= \frac{\text{Cov}(x_k, PC_j)}{\sqrt{\text{Var}(x_k)}\sqrt{\text{Var}(PC_j)} } \\&= \frac{\text{Cov}(Xe_k, Xq_j)}{\sigma_k\sqrt{\lambda_j}} \\& = \frac{e_k^t \text{Var}(X)q_j}{\sigma_k\sqrt{\lambda_j}} \\ &= \frac{\lambda_jq_{jk}}{\sigma_k\sqrt{\lambda_j}} = \frac{\sqrt{\lambda_j}q_{jk}}{\sigma_k \sqrt{\lambda_j}} \end{align}$$
이를 통해 알 수 있는 것은 각 설명변수가 표준화되어 있다면 $x_k$의 분산은 모두 동일할 것이고 그에 따라 $j$번째 주성분에서 $k$번째 계수인 $q_{jk}$의 절대값은 $j$번째 주성분에 대한 $x_k$의 중요도로 해석할 수 있는 것이다.
3) 주성분 개수 정하기
주성분 분석에서는 이론적으로 설명 변수의 개수만큼 계산할 수 있다. 하지만 몇 개의 주성분만 가지고 데이터의 총분산을 대부분 설명할 수 있는 것이 주성분 분석의 큰 특징이다.
그렇다면 몇 개의 주성분을 골라야 하는지에 대한 문제가 생긴다. 이에 대한 명확한 기준은 없으나 데이터 총분산에 대한 누적 설명 비율이 70~80% 이상되는 최소의 주성분을 고를 수 있다. 또는 누적 분산 설명 비율의 증가분을 주성분에 대하여 분산이 큰 순서대로 그린 다음(Elbow Plot) 누적 설명 비율의 증가분이 급감하는 지점까지의 주성분을 선택한다.
3) 알고리즘
주성분 분석의 알고리즘은 다음과 같다.
알고리즘
1 단계) 주성분의 누적 분산 설명 비율의 하한선 $c>0$를 설정한다.
2 단계) $\text{Var}(X)$의 고유값을 계산한 뒤 내림차순으로 정렬한다. $\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_p$
3 단계) 주성분의 누적 분산 설명 비율이 $c$를 넘어가는 최초의 인덱스 $k$를 결정한다. 즉,
$$\frac{\sum_{j=1}^k \lambda_j}{\text{tr}(\text{Cov}(X))}$$
인 최초의 $k$를 설정한다.
4 단계) 주성분 $Xq_1, \ldots, Xq_k$를 계산한다.
4) 주성분 분석의 활용
주성분 분석은 많은 설명 변수를 가진 데이터에 대해서 데이터의 총분산을 잘 설명하는 일부 주성분을 이용하여 회귀 모형을 만드는 데 사용할 수 있다. 즉, 차원 축소를 통한 회귀 모형을 만드는데 주성분 분석이 활용될 수 있다. 이를 주성분 회귀(Principal Component Regression : PCR)이라 하는데 이에 대한 내용은 추후 포스팅할 예정이다.
3. 파이썬 구현
이번엔 주성분 분석을 파이썬으로 구현해 보자. 아래 코드에서 myPCA 클래스는 분산 설명 비율의 상한선을 입력받으며 fit 메서드를 통해 첫 번째 주성분부터 상한선을 최초로 넘게 되는 주성분까지를 구하게 되며 이에 대응하는 성분 벡터(주성분과는 다름)와 분산 설명 비율 등을 계산한다.
class myPCA:
def __init__(self, explained_var_ratio_thres=0.7):
self.explained_var_ratio_thres = explained_var_ratio_thres
self.n_components = None ## 최종 선택된 주성분 개수
self.explained_var = None ## 주성분별 분산 설명 비율
self.components = None ## 성분(축)
self.principal_components = None ## 주성분
self.total_variance = None ## 총 데이터 분산
self.pc_variable_corr_mat = None ## 주성분과 변수간 상관 행렬
def fit(self, X):
c = self.explained_var_ratio_thres
X = X - np.mean(X, axis=0)
n = X.shape[0]
variance_X = (1/(n-1))*X.T @ X
eigen_value, eigen_vector = np.linalg.eig(variance_X)
total_variance = np.sum(eigen_value)
eigen_value, eigen_vector = np.linalg.eig(variance_X)
total_variance = np.sum(eigen_value) ## 데이터 총 분산
explained_var = eigen_value/total_variance ## 주성분별 분산 설명 비율
## 누적 분산 설명 비율이 c를 넘는 최초 인덱스
last_idx = np.min(np.where(np.cumsum(explained_var) > c)[0])
self.n_components = last_idx+1
self.pc_var = eigen_value[:last_idx+1]
self.explained_var = self.pc_var/total_variance
self.components = eigen_vector[:, :last_idx+1]
self.principal_components = X@eigen_vector[:, :last_idx+1]
self.total_variance = total_variance
pc_variable_corr_mat = np.zeros((last_idx+1, X.shape[1]))
for i in range(last_idx+1):
for j in range(X.shape[1]):
pc = self.principal_components[:, i]
variable = X[:, j]
pc_variable_corr_mat[i, j] = np.corrcoef(pc, variable)[0,1]
self.pc_variable_corr_mat = pc_variable_corr_mat
return self
4. 예제
앞에서 구현한 myPCA를 이용하여 실제 데이터에 대한 주성분 분석을 수행해 보자. 여기서는 붓꽃 데이터의 설명 변수만을 이용한 주성분 분석을 해보고자 한다.
아래 코드는 붓꽃 데이터(Iris)를 불러온 뒤 myPCA를 이용하여 주성분 분석을 수행한다. 그러고 나서 최종 선택된 주성분 개수와 각 주성분별로 분산 설명 비율을 계산하고 추가적으로 성분 벡터와 주성분과 설명 변수간 상관 행렬을 출력한다.
from sklearn.datasets import load_iris
iris = load_iris()
X = iris.data
pca = myPCA(0.95).fit(X)
print('선택된 주성분 개수 :', pca.n_components)
print('주성분별 분산 설명 비율 :', pca.explained_var)
print('주성분의 총 분산 설명 비율 :', np.sum(pca.explained_var))
print('성분 벡터 :')
print(pca.components)
print('주성분 vs 변수 상관행렬 :')
print(pca.pc_variable_corr_mat)

결과를 보면 총 4개의 설명 변수 중에서 단 2개의 주성분만으로 데이터의 총분산을 97.8% 설명한다는 것을 알 수 있다.
5. 장단점
주성분 분석(PCA)의 장단점은 다음과 같다.
- 장점 -
a. 주성분 분석을 이용면 차원 축소가 가능하다.
많은 설명 변수를 몇 개의 주성분으로 차원 축소가 가능하며 이를 통해 데이터를 시각화하는데 도움이 될 수 있고 또는 회귀 모형을 학습하는 데 사용할 수도 있다.
b. 다중 공선성이 있는 설명 변수를 상관성이 없는 주성분들로 변환한다.
즉, PCA를 통해 원 데이터를 군더더기 없는(Not Redundant) 데이터로 변환할 수 있다. 이는 예측 모형의 성능을 향상할 가능성이 있다.
c. 계산 속도가 향상된다.
당연하게도 차원 축소를 했으니 계산 속도 또한 향상된다.
d. 구현이 쉽다.
PCA는 코드로 구현하기 쉽다.
- 단점 -
a. 변수를 선택하는 것은 아니다.
각 주성분이 설명 변수의 선형 결합이므로 결국 모든 설명 변수를 활용하기에 변수 선택이 된 것은 아니며 진정한 의미에서의 차원 축소로 보기 어렵다.
b. 주성분의 해석이 어렵다.
주성분은 결국 설명 변수의 선형 결합이므로 주성분을 데이터로써의 의미를 파악하기 어렵다.
c. 최적 주성분 개수를 선택하기 위한 이론적인 방법이 없다.
최적 주성분 개수를 선정하는 것은 일종의 가이드라인만 있을 뿐 이론적인 방법이 없다.
d. Scaling에 민감하다.
PCA는 변수의 Scale에 민감하여 그에 따라 표준화(Standardization)를 필수적으로 수행한다.





댓글