이번 포스팅에서는 다변량 분석 방법 중 하나인 정준 상관 분석(Canonical Correlation Analysis : CCA)에 대한 개념과 파이썬 구현 방법에 대해서 알아보고자 한다.
- 목차 -
1. 정준 상관 분석이란?
1) 정의
정준 상관 분석(Canonical Correlation Analysis : CCA)이란 종속 변수 집단과 설명 변수 집단(또는 독립 변수 집단)의 상관 구조를 잘 설명하는 종속 변수 선형 결합과 설명 변수 선형 결합을 찾고 이러한 선형 결합들을 이용하여 두 변수 집단의 상관성을 효과적으로 분석하는 방법론을 말한다.
2) 파헤치기
앞에서 정의한 내용을 좀 더 자세하게 알아보자.
a. CCA는 종속 변수 집단과 설명 변수 집단의 상관 구조를 잘 설명하는 종속 변수 선형 결합과 설명 변수 선형 결합을 찾는다.
CCA는 먼저 변수 집단을 종속 변수 집단과 설명 변수 집단으로 나눈다. 기존 다변량 회귀 분석 방법은 설명 변수의 선형 결합들 중에서 종속 변수 집단을 (잔차 제곱을 최소화하는 관점에서) 잘 설명하는 선형 결합을 찾았다. 다시 말해 다변량 회귀 분석 방법은 종속 변수 집단의 일반적인 선형 결합을 고려하지 않았던 것이다. 하지만 CCA는 두 변수 집단(종속 변수 집단, 설명 변수 집단)의 선형 결합을 고려하고 그 많은 선형 결합 중에서 두 변수 집단의 상관 구조를 잘 설명하는 선형 결합을 찾게 되는 것이다.
여기서 말하는 상관 구조는 각 변수 집단에서 만들어진 두 선형 결합 간 상관 계수를 의미하며 상관 구조를 잘 설명한다는 것은 상관 계수를 최대화한다는 것을 의미한다.
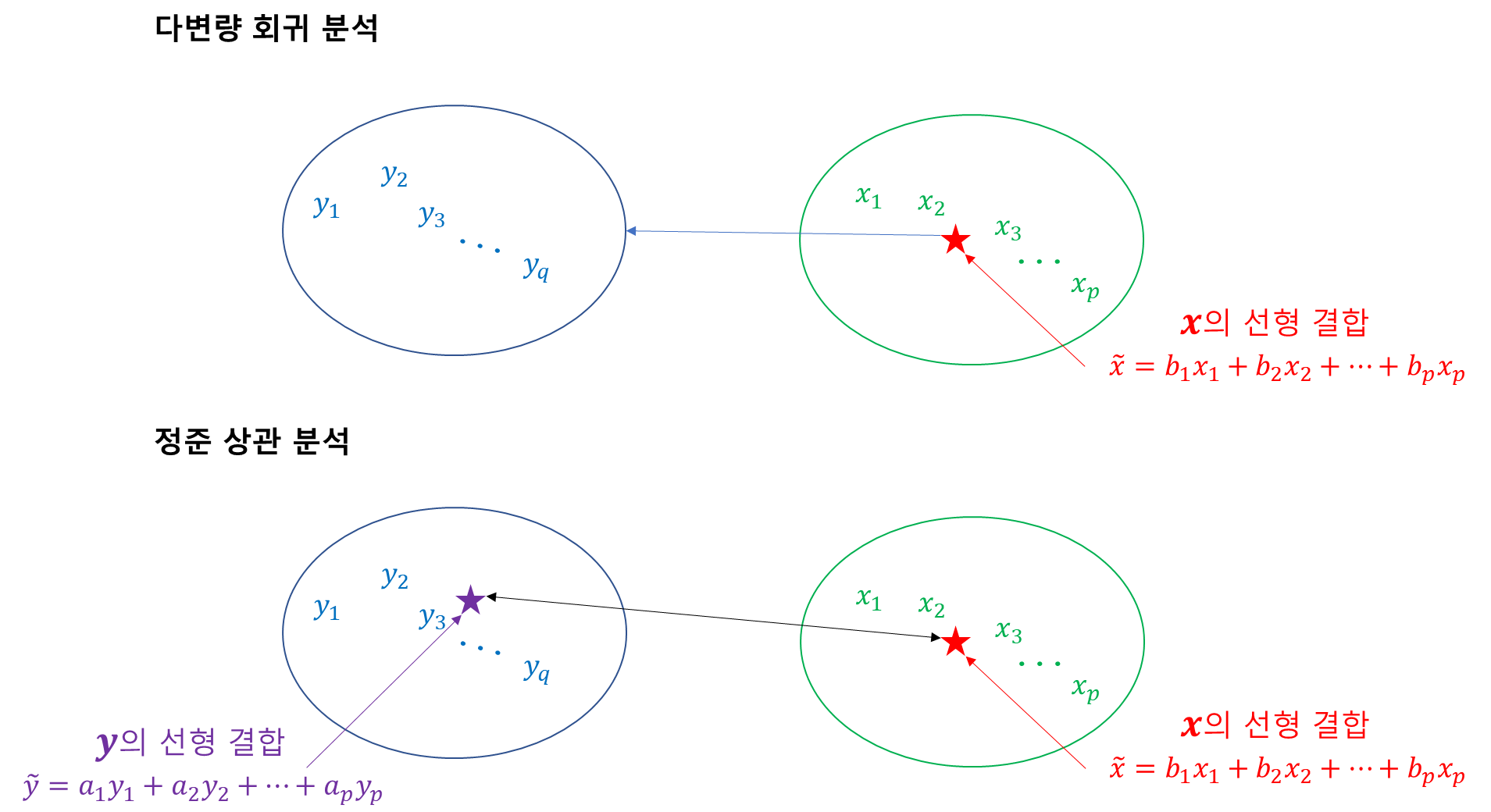
아래 그림은 다변량 회귀 분석과 정준 상관 분석의 차이를 나타낸 것이다. 다변량 회귀 분석(위쪽 그림)은 종속 변수 집단을 잘 설명하는 설명 변수의 선형 결합(빨간 별)을 찾는 것이다. 반면 정준 상관 분석(아래쪽 그림)은 두 변수 집단의 상관 구조를 잘 설명하는 종속 변수의 선형 결합(보라색 별)과 설명 변수의 선형 결합을 찾는 것을 목표로 한다.
b. 선형 결합들과 기존 변수의 상관성을 분석하여 기존 변수들의 의미 또는 영향력을 해석한다.
종속 변수 집단과 설명 변수 집단에 대해서 가장 먼저 생각해 볼 수 있는 것은 종속 변수 하나와 다른 설명 변수 하나를 가지고 변수 쌍을 만든 다음 각 변수 쌍에 대한 상관 계수를 볼 수도 있을 것이다. 하지만 (1) 각 집단 내 변수가 많아질수록 변수 쌍을 모두 고려하여 보는 것이 비효율적이며 (2) 어떤 집단의 변수는 다른 집단의 한 변수에 의존하는 것이 아닌 여러 변수가 동시에 영향을 미칠 수도 있으므로 개별 변수 쌍의 상관 계수를 보는 것이 의미가 없어질 수 있는 것이다.
만약 각 변수 집단을 잘 요약할 수 있는 몇개의 선형 결합을 이용하여 상관성을 분석할 수 있다면 많은 수의 개별 변수 간 상관 계수를 보는 것보다 효과적으로 상관 구조를 파악할 수 있다. 또한 개별 변수 쌍으로는 볼 수 없었던 여러 변수들 간의 의존성을 동시에 볼 수 있는 것이다. 즉, 두 변수 집단의 선형 결합을 이용하면 이러한 장점이 있다는 것이다.
CCA는 각 변수 집단의 상관 구조를 잘 설명하는 선형 결합을 구한다고 했다. 이때 각 선형 결합과 각 집단 내 변수의 상관 계수를 이용하여 선형 결합에 대한 해당 변수의 기여도를 볼 수 있다(아래 그림 참고). 기여도의 구체적인 계산 방법은 아래에서 다뤄보기로 한다.
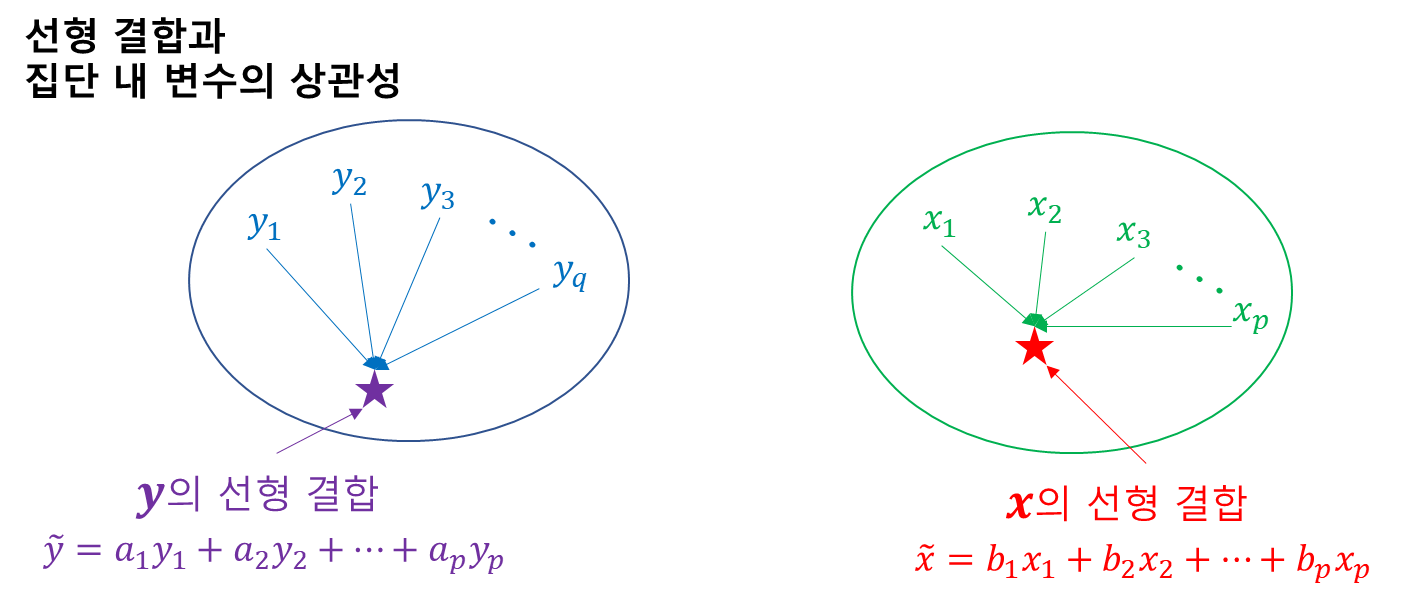
또한 한 집단에서의 변수와 다른 집단의 선형 결합 간 상관 계수를 이용하여 해당 선형 결합에 영향을 미치는 다른 변수의 영향도 또한 볼 수 있다. 아래 그림은 설명 변수와 종속 변수 집단의 선형 결합 간 상관관계를 도식화한 것이다(물론 종속 변수와 설명 변수의 선형 결합 간 상관 관계도 고려한다). 영향도의 계산 방법은 아래에서 다뤄보기로 한다.

2. 분석 절차
이제 정준 상관 분석(CCA)에 대한 개념을 알았으니 CCA의 분석 절차를 알아보자. 전체적인 분석 순서는 나중에 알아보고 먼저 개별적인 분석 절차에 대해서 살펴보기로 한다.
1) 정준 변수 구하기
먼저 변수의 개수는 $p+q$, 관측치의 개수가 $n$인 데이터를 $p$개의 설명 변수 집단 $X$과 $q$개의 종속 변수 집단 $Y$와 나누었다고 하자. 즉,
$$X = \begin{pmatrix} x_{11} & x_{12} & \cdots & x_{1p} \\ x_{21} & x_{22} & \cdots & x_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ x_{n1} & x_{n2} & \cdots & x_{np} \end{pmatrix}, \;\; Y = \begin{pmatrix} y_{11} & y_{12} & \cdots & y_{1q} \\ y_{21} & y_{22} & \cdots & y_{2q} \\ \vdots & \vdots & \ddots & \vdots \\ y_{n1} & y_{n2} & \cdots & y_{nq} \end{pmatrix}$$
편의상 $q \leq p$라 가정하겠다.
이제 $a \in \mathbb{R}^q$에 대하여 종속 변수의 선형결합 $Ya$과 $b \in \mathbb{R}^p$에 대하여 설명 변수의 선형결합 $Xb$을 고려해 보자. 정준 상관 분석(CCA)에서는 표본 상관 계수를 최대화시키는 선형 결합 계수 $a, b$를 찾게 된다.
$$\rho = \text{Corr}(Ya, Xb)= \frac{\text{Cov}(Ya, Xb)}{\sqrt{\text{Var}(Ya)\text{Var}(Xb)}} = \frac{a^t S_{yx} b}{\sqrt{(a^tS_{yy}a)( b^tS_{xx}b)}} \tag{1}$$
여기서 $S_{uv}$는 $U$와 $V$의 표본 공분산 행렬 $\text{Cov}(U, V)$이며 $S_{uv}$의 $i, j$원소는
$$\frac{1}{n-1} \sum_{l=1}^n(u_{li}-\bar{u}_i)(v_{lj}-\bar{v}_j)$$
이며 $\bar{u}_i = \sum_{l=1}^nu_{li}/n, \bar{v}_j = \sum_{l=1}^nv_{lj}/n$이다.
이제 (1)이 언제 최대가 되는지 살펴보자. 먼저 $c_1, d_1$를 다음과 같이 정의하자.
$$c_1 = S_{yy}^{1/2}a, d_1 = S_{xx}^{1/2}b \tag{2}$$
이를 이용하여 (1)을 다시 쓰면 다음과 같다.
$$\rho = \frac{c_1^tS_{yy}^{-1/2}S_{yx}S_{xx}^{-1/2}d_1 }{\sqrt{c_1^tc_1}\sqrt{d_1^td_1}} \tag{3}$$
여기서 Cauchy-Schwarz 부등식을 적용하면 다음과 같다.
$$\left ( c_1^t S_{yy}^{-1/2} S_{yx} S_{xx}^{-1/2} \right ) (d_1) \leq \left ( c_1^t S_{yy}^{-1/2} S_{yx} S_{xx}^{-1/2} S_{xx}^{-1/2} S_{xy} S_{yy}^{-1/2}c_1 \right )^{1/2} (d_1^td_1)^{1/2} $$
양변을 $\sqrt{c_1^tc_1}\sqrt{d_1^td_1}$로 나누어주면
$$\rho \leq \frac{\left ( c_1^t S_{yy}^{-1/2} S_{yx} S_{xx}^{-1}S_{xy} S_{yy}^{-1/2}c_1 \right )^{1/2}}{(c_1^tc_1)^{1/2}} \tag{4}$$
부등식 (4)에서 등호성립조건은 $d_1$가 $S_{xx}^{-1/2} S_{xy} S_{yy}^{-1/2}c_1$과 같은 방향인 경우이다. 그리고 부등식 (4)의 우변은 $\rho$의 상한이라 할 수 있는데 우변이 최대가 되는 경우는 $c_1$가 $S_{yy}^{-1/2} S_{yx} S_{xx}^{-1}S_{xy} S_{yy}^{-1/2}$의 최대 고유값 $\lambda_2$에 해당하는 고유 벡터인 경우이다.
이를 통해 알 수 있는 것은 $c_1$가 $S_{yy}^{-1/2} S_{yx} S_{xx}^{-1}S_{xy} S_{yy}^{-1/2}$의 최대 고유값에 대응되는 고유 벡터이고 $d_1 = \theta S_{xx}^{-1/2} S_{xy} S_{yy}^{-1/2}c_1$인 경우가 된다. 상수 $\theta$는 $d_1$의 길이가 1이 되도록 잡아준다. 그러면 다음을 알 수 있다.
$$1 = d_1^td_1 = \theta^2 c_1^t S_{yy}^{-1/2} S_{yx} S_{xx}^{-1}S_{xy} S_{yy}^{-1/2} c_1 \\ = \theta^2 \lambda_1 c_1^tc_1 = \theta^2\lambda_1$$
즉, $\theta = 1/\sqrt{\lambda_1}$
이렇게 계산된 $c_1, d_1$를 이용하여 (2)를 통해 $a, b$를 다시 역산한다.
$$a = S_{yy}^{-1/2}c_1, \;\;b = S_{xx}^{-1/2}d_1 \tag{4}$$
이를 통해 얻어진 선형 결합
$$w_1 = Ya = YS_{yy}^{-1/2}c_1, \;\; v_1 = Xb = XS_{xx}^{-1/2}d_1 $$
을 첫 번째 정준 변수(또는 정준 변수 쌍)라 한다.
두 번째 정준 변수는 $c_1, d_1$과는 수직이면서 (3)을 최대화하는 벡터 $c_2, d_2$가 된다. 이때 $c_2$는 $S_{yy}^{-1/2} S_{yx} S_{xx}^{-1}S_{xy} S_{yy}^{-1/2}$의 고유값 중 두 번째로 큰 고유값 $\lambda_2$에 대응하는 고유 벡터가 되고 $d_2 = (1/\sqrt{\lambda_2})S_{xx}^{-1/2} S_{xy} S_{yy}^{-1/2}c_2$이다. 이때 $S=S_{yy}^{-1/2} S_{yx} S_{xx}^{-1}S_{xy} S_{yy}^{-1/2}$는 $q\times q$ 행렬이므로 이론적으로 $q$개의 정준 변수를 구할 수 있으며 $i$ 번째 정준 변수 $w_i, v_i$는 $S$의 $i$번째로 큰 고유값과 그에 대응하는 벡터를 이용하여 구할 수 있는 것이다. 이때 $i$ 번째 정준 변수 $w_i, v_i$의 상관 계수를 $i$번째 정준 상관 계수라 하고 $\rho_i$라 표시한다.
이제 정준 변수와 관련된 몇 가지 성질에 대해서 알아보자.
정준 변수의 성질
$S=S_{yy}^{-1/2} S_{yx} S_{xx}^{-1}S_{xy} S_{yy}^{-1/2}$라 하고 $S$의 고유값을 내림차순으로 정렬한 것을 $\lambda_1 \geq \lambda_2 \geq \cdots \lambda_q > 0$라 하자($S$는 양정치 행렬이므로 고유값은 양수이다).
$q$개의 정준 변수들을 $(w_1, v_1), (w_2, v_2), \ldots, (w_q, v_q)$라 할 때 다음이 성립된다.
(a) $\text{Var}(w_i) = \text{Var}(v_i) = 1$
(b) $\text{Corr}(w_i, v_i) = \rho_i = \sqrt{\lambda_i}$
(c) $\text{Cov}(w_i, w_j) = \text{Corr}(w_i, w_j) = 0, \;\; i \neq j $
(d) $\text{Cov}(v_i, v_j) = \text{Corr}(v_i, v_j) = 0, \;\; i \neq j$
(e) $\text{Cov}(w_i, v_j) = \text{Corr}(w_i, v_j) = 0, \;\; i \neq j$
증명
(a) $w_i = YS_{yy}^{-1/2}c_i $이고 $c_i$는 고유 벡터이므로 단위 벡터로 취급하여 $c_i^tc_i=1$
$$\begin{align} \text{Var}(w_i) &= c_i^tS_{yy}^{-1/2}\text{Var}(Y)S_{yy}^{-1/2}c_i \\ &= c_i^tS_{yy}^{-1/2}S_{yy}S_{yy}^{-1/2}c_i \\ &= c_i^t c_i = 1 \end{align}$$
비슷한 방식으로 $\text{Var}(v_i)=1$임을 보일 수 있다.
(b) $w_i = YS_{yy}^{-1/2}c_i, v_i = XS_{xx}^{-1/2}d_i $이므로
$$ \begin{align} \text{Corr}(w_i, v_i) &= \text{Cov}(w_i, v_i) \\ &= c_i^tS_{yy}^{-1/2} \text{Cov}(Y, X) S_{xx}^{-1/2} d_i \\ &= (1/\sqrt{\lambda_i}) c_i^tSc_i = (1/\sqrt{\lambda_i}) \lambda_i = \sqrt{\lambda_i}\end{align}$$
(c) $w_i = YS_{yy}^{-1/2}c_i, w_j = YS_{yy}^{-1/2}c_j $이고 $c_i^tc_j=0$이므로
$$ \begin{align} \text{Cov}(w_i, w_j) = c_i^tS_{yy}^{-1/2}\text{Var}(Y)S_{yy}^{-1/2}c_j = c_i^tc_j =0 \end{align}$$
(d), (e)는 (c)와 비슷한 방법으로 증명할 수 있다.
2) 정준 구조 행렬 구하기
이번엔 (종속 또는 설명) 변수와 정준 변수간 상관관계를 알 수 있는 정준 구조 행렬에 대해서 알아본다. 정준 구조 행렬은 정준 적재 행렬과 정준 교차 적재 행렬이 있다. 이에 대해서 알아보자.
a. 정준 적재 행렬
집단 내 변수와 해당 집단의 정준 변수간 상관 행렬을 정준 적재 행렬이라 하며 정준 적재 행렬은 집단 내 변수들이 정준 변수에 기여하는 기여도를 살펴볼 수 있다.
종속 변수의 개수를 $q$, 독립 변수의 개수를 $p$라 할 때 $q\leq p$라고 가정한다.
종속 변수 집단 $Y$에서 도출할 수 있는 모든 정준 변수는 다음과 같다.
$$\begin{align} w_1 &= a_{11}y_1+a_{12}y_2+ \cdots + a_{1q}y_q \\ w_2 &= a_{21}y_1+a_{22}y_2 + \cdots + a_{2q}y_q \\ \vdots & \;\;\;\;\; \;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\; \vdots \\ w_q &= a_{q1}y_1+a_{q2}y_2 + \cdots +a_{qq}y_q \end{align}$$
여기서 $y_j = (y_{1j}, y_{2j}, \ldots, y_{nj})^t, j=1, 2, \ldots, q$이다. 위 식을 행렬로 쓰면 다음과 같다.
$$W_{n\times q} = YA$$
여기서 $A$의 $j$번째 칼럼 벡터는 $(a_{j1}, a_{j2}, \ldots, a_{jq})^t, j=1, \ldots, q$이다.
이번엔 독립 변수 집단(또는 설명 변수 집단) $X$에서 도출할 수 있는 모든 정준 변수는 다음과 같다.
$$\begin{align} v_1 &= b_{11}x_1+b_{12}x_2+\cdots+b_{1p}x_p \\ v_2 &= b_{21}x_1+b_{22}x_2+\cdots+b_{2p}x_p \\ \vdots & \;\;\;\;\; \;\;\;\;\;\;\;\;\;\; \;\;\;\;\;\;\;\; \vdots \\ v_q &= b_{q1}x_1+b_{q2}x_2 + \cdots +b_{qp}x_p \end{align}$$
여기서 $x_j = (x_{1j}, x_{2j}, \ldots, x_{nj})^t, j=1, 2, \ldots, p$이다. 위 식을 행렬로 쓰면 다음과 같다.
$$V_{n\times q} = XB$$
여기서 $B$의 $j$번째 칼럼 벡터는 $(b_{j1}, b_{j2}, \ldots, b_{jp})^t, j=1, \ldots, q$이다.
이제 종속 변수 집단으로부터 유도된 $i$ 정준 변수 $w_i$와 $k$ 번째 종속 변수 $y_k$의 상관 계수를 계산해보자. $\text{Var}(w_i)=1$임을 이용하면 다음을 알 수 있다.
$$\text{Corr}(w_i, y_k) = \frac{\text{Cov}(w_i, y_k)}{\sqrt{\text{Var}(w_i)\text{Var}(y_k)}} = \frac{\text{Cov}(w_i, y_k)}{s_{y, k}} \tag{5}$$
여기서 $\text{Var}(y_k) = s_{y, k}^2$으로 $y_k$의 표본 분산을 의미한다.
(5)는 $i$ 정준 변수 $w_i$와 $k$ 번째 종속 변수 $y_k$의 정준 적재라고도 하며 이 값이 높을수록 종속 변수 $y_k$가 정준 변수 $w_i$에 많은 기여를 했다고 해석한다(큰 영향을 미쳤다고 하는 것과 동일하다).
(5)는 다음과 같이 쓸 수 있다.
$$\text{Corr}(w_i, y_k) = \text{Cov}(w_i, s_{y, k}^{-1} y_k) \tag{6}$$
(6)을 이용하면 종속 변수 집단 $Y$와 이에 대응하는 정준 변수 집단 $W = (w_1 \; w_2 \; \cdots \; w_q)$의 상관 행렬인 정준 적재 행렬은 다음과 같이 구할 수 있다.
$$\text{Corr}(W, Y) = \text{Cov}(YA, D_y^{-1/2}Y) = A^tS_{yy}D_y^{-1/2} \tag{7}$$
여기서 $D_y^{-1/2}$은 $k$번째 대각 원소가 $s_{y, k}^{-1}$인 대각 행렬이다.
비슷한 방법으로 독립 변수 집단 $X$와 이에 대응하는 정준 변수 집단 $V = (v_1 \; v_2 \; \cdots \; v_q)$의 정준 적재 행렬은 다음과 같이 계산된다.
$$\text{Corr}(V, X) = \text{Cov}(XB, D_x^{-1/2}X) = B^tS_{xx}D_x^{-1/2} \tag{8}$$
여기서 $D_x^{-1/2}$은 $k$번째 대각 원소가 $s_{x, k}^{-1}$인 대각 행렬이다.
b. 정준 적재 교차 행렬
한 집단 내 변수와 다른 집단의 정준 변수간 상관 행렬을 정준 교차 적재 행렬이라하며 정준 교차 적재 행렬은 한 집단 내 변수가 다른 집단의 정준 변수에 미치는 영향력을 살펴볼 수 있다.
종속 변수 집단에서 도출된 $i$ 번째 정준 변수 $W_i$와 $k$번째 독립 변수 $x_k$의 상관 계수인 정준 교차 적재를 살펴보면
$$\text{Corr}(w_i, x_k) = \frac{\text{Cov}(w_i, x_k)}{\sqrt{\text{Var}(w_i)\text{Var}(x_k)}} = \frac{\text{Cov}(w_i, x_k)}{s_{x, k}} \tag{9}$$
(9)에서 정준 교차 적재 값이 높을수록 독립변수 $x_k$가 종속 변수 집단의 정준 변수 $w_i$에 큰 영향을 미친다고 해석한다. 따라서 종속 변수 집단의 정준 변수 집단 $W$와 독립 변수 집단 $X$의 상관행렬인 정준 교차 적재 행렬은 다음과 같이 구할 수 있다.
$$\text{Corr}(W, X) = \text{Cov}(YA, D_x^{-1/2}X) = A^tS_{yx}D_x^{-1/2} \tag{10}$$
마찬가지로 독립 변수 집단의 정준 변수 집단 $V$와 종속 변수 집단 $Y$의 정준 교차 적재 행렬은 다음과 같이 계산할 수 있다.
$$\text{Corr}(V, Y) = \text{Cov}(XB, D_y^{-1/2}Y) = B^tS_{xy}D_y^{-1/2} \tag{11}$$
3) 설명력
각 집단 내에서 도출된 정준 변수들이 각 집단을 얼마나 잘 요약하고 있는지 다시 말해 얼마나 잘 대표하는지 살펴볼 필요가 있다. 정준 변수가 집단 변수를 잘 대표하는지에 대한 측도는 집단 내 총 분산에 대한 정준 변수의 설명 비율을 사용한다.
설명 비율을 계산할 때에는 모든 변수가 표준화되어 있다고 가정한다. 그렇다면 $Y$의 총분산은 $q$개의 표준화된 종속 변수의 분산합이므로 $q$가 될 것이다. 이때 $i$ 번째 정준 변수 $w_i$에 대한 집단 설명 비율 $R_i^2(Y|w_i)$은 다음과 같다.
$$R_i^2(Y|w_i) = \frac{\sum_{j=1}^q\text{Corr}^2(w_i, y_j)}{q}\tag{12}$$
$R_i^2(Y|w_i)$ 값이 높을수록 $i$ 번째 정준 변수는 집단 내 분산 구조에 대한 설명력이 높다는 뜻이며 이는 집단을 잘 요약한다고 볼 수 있으며 이는 집단 내 모든 변수를 사용하는 것보다 정준 변수를 이용하여 상관성을 보는 것이 더 효과적임을 뜻한다.
개별 정준 변수에 대한 설명 비율을 볼 수도 있지만 처음 $m(\leq q)$개의 종속 변수 집단의 정준 변수가 설명하는 누적 설명 비율도 살펴볼 필요가 있는데 이는 다음과 같이 계산할 수 있다.
$$\frac{\sum_{i=1}^m\sum_{j=1}^q \text{Corr}^2(w_i, y_j) }{q}\tag{13}$$
(13)을 비율로 해석하려면 그 값이 0과 1 사이여야 할 것이다. 분모 분자가 모두 양수이므로 (13)이 1보다 작음을 증명하면 된다. $m\leq q$에 대하여 (13)의 분자를 살펴보자.
$$\begin{align} \sum_{i=1}^m\sum_{j=1}^q \text{Corr}^2(w_i, y_j) &\leq \sum_{i=1}^q\sum_{j=1}^q \text{Corr}^2(w_i, y_j) \\ &= \| \text{Corr}(W, Y) \|_F^2 \\ &= \text{tr} \left ( \text{Corr}(W, Y) \text{Corr}(W, Y)^t \right ) \\ &= \text{tr} \left ( A^tS_{yy}D_y^{-1/2} (D_y^{-1/2} S_{yy} A) \right ) \\ &= \text{tr} \left ( D_y^{-1/2}S_{yy}AA^tS_{yy}D_y^{-1/2}\right ) \\ &= \text{tr} \left ( D_y^{-1/2}S_{yy}S_{yy}^{-1}S_{yy}D_y^{-1/2}\right ) \\ &= \text{tr} \left ( D_y^{-1/2}S_{yy}D_y^{-1/2}\right ) \\ &= \text{tr} \left (S_{yy}\right ) \leq q \end{align}$$
여기서 $\| \cdot \|_F^2$는 Frobenius Norm이며 위 증명에서 $AA^t = S_{yy}^{-1/2}CC^tS_{yy}^{-1/2}$이고 $C$는 Orthonormal 행렬이므로 $AA^t = S_{yy}^{-1}$이 된다는 사실을 이용하였다. 따라서 위 양변에 $q$로 나누어주면 (13)은 1보다 작거나 같은 값을 가지게 되어 비율로 해석할 수 있다. 물론 (13) 보다 작은 (12) 또한 비율로 해석가능하다.
마찬가지로 독립 변수 집단 $X$에 대한 독립 변수 집단의 $i$번째 정준 변수 $V$의 설명력을 위와 동일한 방식으로 정의할 수 있다.
$$R_i^2(X|v_i) = \frac{\sum_{j=1}^p\text{Corr}^2(v_i, y_j)}{p}\tag{14}$$
그리고 처음 $l$개의 독립 변수 집단의 정준 변수들에 의하여 설명되는 누적 비율을 다음과 같이 계산할 수 있다.
$$\frac{\sum_{i=1}^l\sum_{j=1}^p\text{Corr}^2(v_i, y_j)}{p}\tag{15}$$
이번엔 독립 변수 집단으로부터 도출한 정준 변수 $v_i$가 종속 변수 집단 $Y$를 얼마나 잘 설명하는지에 대한 측도 $R_i^2(Y|v_i)$는 다음과 같이 계산된다.
$$ R_i^2(Y|v_i) = R_i^2(Y|w_i)\rho_i^2\tag{16}$$
(16)은 독립 변수 집단으로부터 생성된 $i$번째 정준 변수 $v_i$가 종속 변수 집단의 분산을 잘 설명하는지에 대한 설명력으로 볼 수 있으며 이를 중복 계수라고도 한다. $\rho^2 \leq 1$이므로
$$ R_i^2(Y|v_i) \leq R_i^2(Y|w_i) \tag{17}$$
이다. 또한 처음 $m$개의 독립 변수의 정준 변수들이 종속 변수 집단의 분산을 잘 설명하는 누적 설명 비율도 고려할 수 있다.
(17)의 부등식은 종속 변수 집단의 분산은 종속 변수로 부터 생성된 정준 변수 $w_i$ 가 $v_i$보다는 더 잘 설명할 수 있어야 한다는 자연스러운 해석을 할 수 있다.
4) 통계적 검정
만약 종속 변수 집단 $Y$ 독립 변수 집단 $X$의 상관관계가 없다면 표본 공분산 행렬 $S_{yx} \approx 0$이고 정준 변수 $w, v$의 표본 공분산은 $a^tS_{yx}b \approx 0$이 되어 정준 상고나 분석을 수행할 필요가 없게 된다. 따라서 정준 상관 분석(CCA)를 하기전에 두 변수 집단 사이의 유의한 상관 관계가 있는지 통계적 검정을 수행할 필요가 있다.
Wilks는 모 공분산 행렬 $\Sigma_{yx}=0$의 여부를 검정하는 검정 통계량을 이용하여 다음과 같이 제안했다.
$$F^* = \frac{[(1-\Lambda^{1/s})/pq] }{ [\Lambda^{1/s}/\{ ms -(pq/2)+1 \} ]} \tag{18}$$
이때 $\Lambda = \prod_{i=1}^p \left (1-\rho_i^2 \right )$이고
$$\begin{align} m &= n-1.5 - (p+q)/2 \\ s &= \sqrt{p^2q^2-4}/\sqrt{p^2+q^2-5} \end{align}$$
이며 $n$은 데이터 개수이고 $\rho_i$는 $w_i, v_i$의 정준 상관 계수이다.
$F^*$는 귀무가설이 참일 때 분자의 자유도가 $pq$이고 분모의 자유도가 $ms-(pq)/2+1$인 $F$ 분포에 근사한다. $p$-value는 $P(F_{pq, ms-(pq)/2+1} > F*)$으로 계산할 수 있으며 유의 수준 $\alpha$에서 구한 기각값(오른쪽 꼬리값이 $\alpha$가 되는 값)을 $F_{\alpha}$이라 할 때 $p$-value가 $F_{\alpha}$보다 크다면 기각하고 아니라면 귀무가설($H_0 : \Sigma_{yx}=0$)을 채택한다.
여기서 소개한 검정은 두 변수 집단이 다변량 정규분포를 따른다는 가정이 필요하며 데이터의 크기 $n$이 충분히 큰 경우에 적용할 수 있다고 한다.
5) CCA 분석 절차
CCA는 (1) 정준 변수를 구하고 이를 이용하여 (2) 상관 행렬에 대한 유의성 검정을 수행한다. 만약 귀무가설을 채택한다면 CCA를 종료하고 기각한다면 (3) 정준 변수의 계수와 정준 적재 행렬을 계산하여 상관성 분석을 수행하고 (4) 정준 변수들의 설명력을 체크한다.

3. 파이썬 구현
이제 정준 상관 분석 과정을 파이썬으로 구현해보고자 한다.
아래 코드에서 CCA 클래스는 정준 상관 분석을 수행한다. CCA에서 analyzing 메서드는 정준 변수를 구하고 상관 행렬에 대한 통계적 검정을 수행한다. 이때 상관 행렬에 대한 귀무가설을 채택한다면 정준 상관 분석을 종료하고 기각한다면 정준 상관 분석을 수행하게 된다.
import numpy as np
import pandas as pd
from scipy.stats import f
class CCA:
def __init__(self):
self.rank = None ## 계산 가능한 정준 변수 개수(종속 변수와 설명 변수 개수의 최소값)
self.x_canonical_var = None ## 설명 변수 집단 정준 변수
self.y_canonical_var = None ## 종속 변수 집단 정준 변수
self.x_canonical_weight = None ## 설명 변수 집단 정준 변수 가중치
self.y_canonical_weight = None ## 종속 변수 집단 정준 변수 가중치
self.x_canonical_loadings = None ## 설명 변수 집단 정준 적재
self.y_canonical_loadings = None ## 종속 변수 집단 정준 적재
self.x_canonical_cross_loadings = None ## 설명 변수와 종속 정준 변수 정준 교차 적재
self.y_canonical_cross_loadings = None ## 종속 변수와 설명 정준 변수 정준 교차 적재
self.test_stat = None ## 상관 행렬 검정 통계량
self.p_value = None ## p 밸류
self.canonical_correlation = None ## 정준 상관 계수
self.eigen_values = None ## 고유값
def analyzing(self, X, Y, alpha=0.1):
p, q, n = X.shape[1], Y.shape[1], X.shape[0]
self.get_canonical_var(X, Y) ## 정준 변수 구하기
self.wilks_test(p, q, n) ## 상관 행렬의 통계적 검정
if alpha < self.p_value:
print('CCA may be not necessary')
else:
self.get_canonical_loadings(X, Y) ## 정준 적재 행렬 계산
self.get_explained_ratio(p, q) ## 설명 비율과 중복 계수 계산
print('CCA completed!')
return self
def wilks_test(self, p, q, n):
## 윌크스 람다 테스트
lamb = np.prod(1-self.eigen_values)
m = n-1.5-(p+q)/2
s = np.sqrt(np.square(p*q)-4)/np.sqrt(p**2+q**2-5)
num = (1-np.power(lamb, 1/s))/(p*q)
denom = np.power(lamb, 1/s)/(m*s-0.5*p*q+1)
F = num/denom
self.test_stat = F
self.p_value = 1-f.cdf(F,dfn=p*q, dfd=m*s-0.5*p*q+1)
def get_sqrt_matrix(self, mat):
## 제곱근 행렬
evalues, evectors = np.linalg.eigh(mat) ## 대칭행렬이므로 eigh
sqrt_matrix = evectors * np.sqrt(evalues) @ evectors.T
return sqrt_matrix
def get_canonical_loadings(self, X, Y):
p = X.shape[1]
q = Y.shape[1]
rank = self.rank
V = self.x_canonical_var
W = self.y_canonical_var
st_Y, st_X = self.standardized_mat(X, Y)
self.x_canonical_loadings = np.corrcoef(st_X.T, V.T)[p:,:rank].T
self.y_canonical_loadings = np.corrcoef(st_Y.T, W.T)[q:,:rank].T
self.x_canonical_cross_loadings = np.corrcoef(st_X.T, W.T)[p:,:rank].T
self.y_canonical_cross_loadings = np.corrcoef(st_Y.T, V.T)[q:,:rank].T
def standardized_mat(self, X, Y):
st_Y = (Y-np.mean(Y, axis=0))/np.std(Y, axis=0, ddof=True)
st_X = (X-np.mean(X, axis=0))/np.std(X, axis=0, ddof=True)
return st_Y, st_X
def get_canonical_var(self, X, Y):
## 정준 변수 계산
n = X.shape[0]
rank = np.min((X.shape[1], Y.shape[1]))
st_Y, st_X = self.standardized_mat(X, Y)
S_xx = (1/(n-1))*st_X.T @ st_X
S_yy = (1/(n-1))*st_Y.T @ st_Y
S_xy = (1/(n-1))*st_X.T @ st_Y
S_yx = (1/(n-1))*st_Y.T @ st_X
inv_S_yy = np.linalg.inv(S_yy)
inv_S_xx = np.linalg.inv(S_xx)
sqrt_S_yy = self.get_sqrt_matrix(S_yy)
sqrt_S_xx = self.get_sqrt_matrix(S_xx)
inv_sqrt_S_yy = np.linalg.inv(sqrt_S_yy)
inv_sqrt_S_xx = np.linalg.inv(sqrt_S_xx)
target_matrix = inv_sqrt_S_yy @ S_yx @ inv_S_xx @ S_xy @ inv_sqrt_S_yy
evalues, evectors = np.linalg.eigh(target_matrix)
evalues = evalues[::-1][:rank]
c_vectors = evectors[:rank, ::-1]
d_vectors = (inv_sqrt_S_xx@S_xy@inv_sqrt_S_yy@c_vectors)/evalues
A = inv_sqrt_S_yy@c_vectors
B = inv_sqrt_S_xx@d_vectors
W = st_Y@A
V = st_X@B
self.rank = rank
self.eigen_values = evalues
self.canonical_correlation = np.sqrt(evalues)
self.x_canonical_var = V
self.y_canonical_var = W
self.x_canonical_weight = B
self.y_canonical_weight = A
def get_explained_ratio(self, p, q):
## 설명 비율, 중복 계수 구하기
y_canonical_loadings = self.y_canonical_loadings
x_canonical_loadings = self.x_canonical_loadings
y_within_explained_ratio = np.sum(np.square(y_canonical_loadings), axis=0)/q
x_within_explained_ratio = np.sum(np.square(x_canonical_loadings), axis=0)/p
self.y_within_explained_ratio = y_within_explained_ratio
self.x_within_explained_ratio = x_within_explained_ratio
self.y_between_explained_ratio = y_within_explained_ratio*self.eigen_values
self.x_between_explained_ratio = x_within_explained_ratio*self.eigen_values4. 예제
여기서는 어느 헬스클럽의 중년남자로부터 측정된 3개의 생리적 변수(몸무게, 허리둘레, 맥박수)와 3개의 운동량 측정 변수(턱걸이, 윗몸일으키기, 멀리뛰기) 데이터를 사용한다. 이때 생리적 변수를 설명 변수 집단, 운동량 측정 변수를 종속 변수 집단으로 하여 정준 상관 분석을 수행해 보자.
데이터는 아래에 첨부해 두었으니 다운받으면 된다.
데이터를 설명 변수 집단과 종속 변수 집단으로 나누어 준다.
df = pd.read_excel('cca_data.xlsx')
X = df[['Weight', 'Waist', 'Pulse']].values ## 설명 변수 집단
Y = df[['Chins', 'Situps', 'Jumps']].values ## 종속 변수 집단
이제 CCA 클래스의 analyzing 메서드를 통하여 정준 상관 분석을 수행한다.
cca = CCA().analyzing(X,Y) ## 정준 상관 분석 시행

CCA가 완료되었다는 문장이 출력된 걸로 봐서 정준 상관 분석이 잘 된 것 같다. 그 결과를 하나씩 살펴보자.
1) 상관 행렬 검정
먼저 상관 행렬에 대한 통계적 검정 결과를 살펴보자. (18)의 검정 통계량과 $p$-value를 계산해 보자.
print('검정 통계량 :', cca.test_stat)
print('P Value :', cca.p_value)

검정 통계량은 2.048이고 이에 대한 $p$-value는 0.064이다. 유의 수준 0.1에서는 귀무가설을 기각할 수 있으므로 종속 변수 집단과 설명 변수 집단의 상관성이 어느 정도 있다고 판단된다.
2) 상관성 분석
정준 변수의 계수를 확인해 보자. 아래 코드는 설명 변수 집단에서 유도된 정준 변수의 계수를 정리한 것이다.
x_weight =pd.DataFrame(cca.x_canonical_weight,
columns=['v1', 'v2', 'v3'],
index=['Weight', 'Waist', 'Pulse'])
x_weight

위 결과를 통해 정준 변수 계수와 표준화된 설명 변수 간의 영향력을 볼 수 있다. 예를 들어 설명 변수 집단의 첫 번째 정준 변수 $v_1$은 다음과 같이 표시된다.
$$v_1 = -0.975\cdot \text{Weight} +1.985\cdot \text{Waist} -0.074\cdot \text{Pulse} \tag{19}$$
이를 통해 첫 번째 정준 변수는 허리 둘레(1.985)와 몸무게(-0.975)에 더 큰 가중치를 두고 있으며 맥박수(-0.074)가 미치는 영향은 거의 없다고 볼 수 있다.
이번엔 설명 변수와 설명 변수 집단에 대응하는 정준 변수 간 상관관계를 살펴보자. 아래 코드는 설명 변수의 정준 적재 행렬을 정리한 것이다.
x_ccv_correlation =pd.DataFrame(cca.x_canonical_loadings,
columns=['v1', 'v2', 'v3'],
index=['Weight', 'Waist', 'Pulse'])
x_ccv_correlation
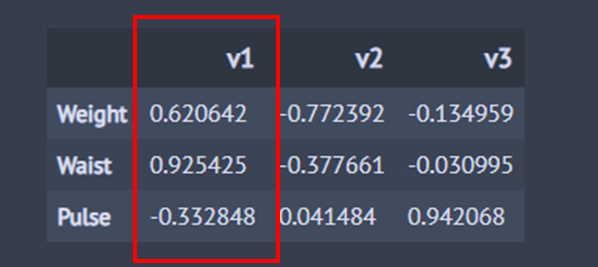
정준 적재 행렬을 통해 정준 변수와 설명 변수간 상관성을 확인할 수 있다. 허리둘레와 첫 번째 정준 상관 변수의 상관 계수는 0.925이며 상관성이 매우 높다. 이는 (19)의 결과와도 일치한다. 하지만 첫 번째 정준 상관 변수는 몸무게와의 상관 계수가 0.621 임에도 불구하고 (19)에서의 계수 부호가 음수였다. 이는 몸무게와 허리둘레의 상관 계수가 아래와 같이 0.870으로 매우 높으며 다중 공선성에 의한 부호 바뀜 현상으로 생각할 수 있다.
np.corrcoef(df['Weight'], df['Waist'])[0, 1]
이번엔 정준 교차 적재 행렬을 통해 설명 변수 집단의 정준 변수와 운동량 측정 변수간 상관성을 살펴보자. 아래 코드는 정준 교차 적재 행렬을 정리한 것이다.
y_ccv_cross_correlation =pd.DataFrame(cca.y_canonical_cross_loadings,
columns=['v1', 'v2', 'v3'],
index=['Chins', 'Situps', 'Jumps'])
y_ccv_cross_correlation
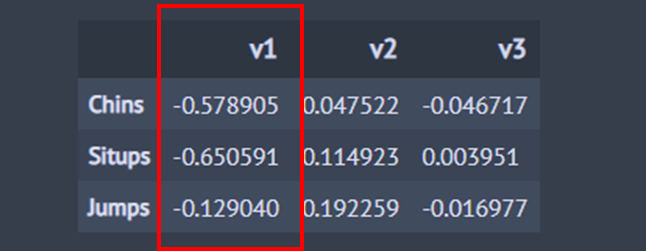
위 결과를 보면 첫 번째 정준 상관 변수는 턱걸이(-0.579)와 윗몸일으키기 횟수(-0.651)와의 음의 상관 관계가 있음을 알 수 있다. 이를 해석하면 첫 번째 정준 상관 변수 $v_1$은 (19)를 통해 $v_1$이 커짐에 따라 뚱뚱한 사람이라고 예상할 수 있으므로 그에 따라 턱걸이와 윗몸 일으키기 횟수가 감소한다는 것이다.
여기서는 설명 변수의 정준 변수에 대한 분석을 했지만 종속 변수의 정준 변수에 대한 분석도 위와 같은 방식으로 할 수 있다.
3) 정준 변수 설명력 확인
이번엔 설명 비율과 중복 계수를 살펴보자. 아래 코드는 종속 변수 집단의 정준 변수의 설명 비율과 누적 설명 비율을 정리한 것이다.
cca_redundacy_df = pd.DataFrame()
cca_redundacy_df['Explained_Proportion'] = cca.y_within_explained_ratio
cca_redundacy_df['Cumulative_Explained_Proportion'] = np.cumsum(cca.y_within_explained_ratio)
cca_redundacy_df

위 결과를 보면 첫 번째 정준 변수의 설명 비율은 0.408, 두 번째 정준 변수의 설명 비율은 0.434이고 두 정준 변수의 누적 비율은 0.8426으로써 첫 번째와 두 번째 정준 변수가 종속 변수 집단을 잘 요약한다고 볼 수 있다.
이번엔 설명 변수 집단의 정준 변수가 종속 변수의 분산을 잘 요약하는지 살펴보자. 아래 코드는 설명 변수 집단의 정준 변수에 대한 설명 비율(중복 계수)과 누적 설명 비율을 정리한 것이다.
cca_duplication_df = pd.DataFrame()
cca_duplication_df['Explained_Proportion'] = cca.y_between_explained_ratio
cca_duplication_df['Cumulative_Explained_Proportion'] = np.cumsum(cca.y_between_explained_ratio)
cca_duplication_df

위 결과를 보면 설명 변수 집단의 첫 번째 정준 변수에 의하여 종속 변수 집단의 분산이 설명되는 비율은 0.258인 것을 알 수 있으며 나머지 정준 변수에 의하여 설명되는 비율은 매우 작은 것을 알 수 있다.
5. 장단점
정준 상관 분석(CCA)의 장단점은 다음과 같다.
- 장점 -
a. CCA는 기존 변수들이 잡아내지 못했던 상관관계를 정준 변수를 통하여 변수 집단 간 상관 관계를 통하여 잡아 낼 수 있다.
b. 변수의 수가 많은 경우 설명 비율을 통해 집단 내 분산 구조를 잘 요약하는 일부의 정준 변수를 가지고 상관성 분석을 할 수 있으므로 일종의 차원 축소 효과가 있는 것이다.
c. 구현이 어렵지 않다.
- 단점 -
a. CCA는 변수 집단 간 선형 관계를 기본적으로 가정하고 있으므로 선형이 아닌 복잡한 관계가 있다면 CCA는 상관성을 적절하게 검출할 수 없다.
b. CCA는 이상치에 민감하다.
통계적 검정 시 다변량 정규 분포를 가정하고 있는데 이상치가 존재한다면 통계적 검정의 결과를 신뢰할 수 없으며 정준 상관 분석 결과 자체에도 이상치가 영향을 줄 수 있어서 분석 결과의 신뢰도가 하락할 수 있다.
c. 대용량 데이터 셋에 대한 컴퓨팅 자원이 많이 들어간다.
정준 상관 분석은 행렬 계산이 많이 포함되어 있어 대용량 데이터 셋에 대한 계산량이 많아질 수 있다.
- 참고 자료 -
성웅현 - 응용 다변량분석
'통계 > 머신러닝' 카테고리의 다른 글
| 41. One-class Support Vector Machine(1-SVM)에 대하여 알아보자 with Python (0) | 2023.05.12 |
|---|---|
| 40. 인자 분석(Factor Analysis)에 대해서 알아보자 with Python (0) | 2023.05.03 |
| 38. 부분 최소 제곱 회귀(Partial Least Square Regression : PLSR)에 대해서 알아보자 with Python (5) | 2023.04.08 |
| 37. 주성분 분석(Principal Component Analysis : PCA)에 대해서 알아보자 with Python (0) | 2023.04.01 |
| 36. Reduced Rank Regression(RRR)에 대해서 알아보자 with Python (2) | 2023.03.16 |





댓글