이번 포스팅에서는 부분 최소 제곱 회귀(Partial Least Square Regression : PLSR)에 대한 개념과 파이썬 구현 방법을 알아보고자 한다.
- 목차 -
1. 부분 최소 제곱 회귀(Partial Least Square Regression : PLSR)란?
PLSR을 이해하기 위해선 주성분 분석에 대한 이해가 필요하다. 아래 포스팅에 주성분 분석에 대한 내용을 정리해 두었으니 참고하면 된다.
37. 주성분 분석(Principal Component Analysis : PCA)에 대해서 알아보자 with Python
37. 주성분 분석(Principal Component Analysis : PCA)에 대해서 알아보자 with Python
이번 포스팅에서는 주성분 분석(Principal Component Analysis : PCA)에 대한 개념과 파이썬(Python)을 이용하여 구현하는 방법에 대해서 알아본다. - 목차 - 1. 주성분 분석이란? 2. 주성분 구하기 3. 파이썬
zephyrus1111.tistory.com
1. 부분 최소 제곱 회귀(Partial Least Square Regression : PLSR)란?
1) 정의
부분 최소 제곱 회귀(Partial Least Square Regression : PLSR)는 반응 변수들을 잘 설명하고 기존 설명 변수의 분산 구조까지 잘 반영한 (설명 변수의) 선형 결합들을 이용하여 회귀 모형을 추정하는 방법을 말한다. PLSR은 필요에 따라 설명 변수의 선형 결합 개수를 조절하여 차원 축소를 할 수도 있다.
2) 파헤치기
위에서 정의한 부분 최소 제곱 회귀(Partial Least Square Regression : PLSR)에 대해서 하나 하나 파헤쳐보자.
a. PLSR은 설명 변수의 선형 결합을 이용한다.
먼저 설명 변수가 ˜xj=(x1j,x2j,…,xnj)t,j=1,…,p 있다. 즉, 데이터 개수는 n개이고 변수의 개수는 p개이다.
설명 변수의 선형 결합이란 p개의 설명 변수의 선형 조합(Linear Combination) t를 의미한다.
t=w1˜x1+w2˜x2+⋯+wp˜xp
이를 행렬과 벡터로 표현하면 다음과 같다.
t=Xw
여기서 X=(˜x1˜x2⋯˜xp)인 n×p 행렬이고 w=(w1,w2,…,wp)t 이다.
PLSR은 설명 변수의 결합들 t1,t2,…을 이용한다. t1,t2,…을 추정하는 자세한 방법은 아래에서 다룬다.
b. PLSR은 반응 변수들을 잘 설명하고 설명 변수의 분산 구조를 잘 반영한 선형 결합을 찾는다.
PLSR은 반응 변수들을 잘 설명하는 설명 변수의 선형 결합을 찾게 된다. 여기서 반응 변수를 잘 설명한다는 것은 반응 변수와의 상관성을 크게 하는 선형 결합을 찾는다는 것이고 설명 변수 분산 구조를 잘 반영한다는 것은 설명 변수들의 선형 결합의 분산을 크게하는 성분을 찾는 것이다. 이를 수식으로 표현해 보자.
먼저 공분산과 분산 그리고 상관 행렬을 다음과 같이 정의한다.
Cov(X,Y)=1n−1XtYVar(X)=Cov(X,X)Corr(X,Y)=Var(X)−1/2Cov(X,Y)Var(Y)−1/2
공분산과 분산 그리고 상관 행렬은 X,Y가 모두 행렬인 경우 행렬, 하나는 행렬 하나는 벡터인 경우 벡터 그리고 둘다 벡터인 경우 실수값이 된다는 것을 알 수 있다.
반응 변수가 ˜yl=(y1l,y2l,…ynl),l=1,…,q로 주어졌다고 해보자. 그리고 Y=(˜y1˜y2⋅˜yq)는 n×q 반응 변수 행렬이다. PLSR은 설명 변수 선형 결합의 분산 그리고 반응 변수 행렬과의 상관 벡터의 이차 형식을 최대화하는 w를 찾는다.
Var(Xw)andCorr(Y,Xw)tCorr(Y,Xw)
(1.3)에 대한 수학적 증명은 다음 섹션에서 다루기로 하고 여기서는 (1.3)을 최대화하는 것의 의미를 살펴보자.
(1.3)에 첫 번째 항은 설명 변수의 선형 결합 분산을 의미한다. PLSR은 이러한 분산을 최대화하는 축 w를 찾는다. 설명 변수 선형 결합의 분산을 최대화한다는 것은 데이터의 변동을 잘 설명하는 축을 찾는 것이라는 것을 주성분 분석 포스팅에서 다루었다. 아래 그림에서 두 개의 축 w1,w2을 보면 w2가 시각적으로 데이터의 변동을 잘 설명하는 방향이며 이때 선형 결합의 분산 Var(Xw2)이 더 큰 것을 알 수 있다(왜냐하면 Xw는 빨간 점을 중심으로 하여 파란 점을 초록색 축에 투영했을 때 생기는 데이터들의 분산과 같기 때문이다).

(1.3)의 두 번째 항은 반응 변수와 설명 변수의 선형 결합 간 상관성에 대한 것이다. PLSR은 반응 변수와의 상관성이 높은 선형 결합을 찾는다. 요약하면PLSR은 기존 주성분 분석에서 찾은 축을 찾는 것과 동시에 반응 변수의 상관성까지 고려한 회귀 방법론인 것이다.
c. PLSR은 일부의 선형 결합을 사용하여 회귀 모형을 추정할 수 있다. 즉, 차원 축소 모형을 만들 수 있다.
PLSR은 설명 변수의 선형 결합을 새로운 변수로 사용한다. PLSR은 선형 결합의 일부를 사용하여 회귀 모형을 추정함으로써 차원 축소를 가능하게 한다.
3) 추정 방법
PLSR에서 설명 변수의 선형 결합을 계산하는 알고리즘을 이해하려면 먼저 Power Iteration 알고리즘(또는 Power Method)의 개념을 알아야 한다. 따라서 이에 대한 내용을 간략하게 소개한다.
a. Power Iteration 알고리즘(Power Method)
Power Iteration은 어떤 행렬 A의 절대값이 큰 고유값을 찾는 알고리즘이며 굉장히 단순하다. 알고리즘은 다음과 같다.
Power Iteration 알고리즘
n×n 정방 행렬 A가 주어졌을 때 Power Iteration 알고리즘은 다음과 같다.
(1 단계) 오차 한계 ϵ>0와 초기 벡터 b0를 세팅한다. 이때 b0는 절대값이 큰 고유값에 해당하는 고유 벡터를 잘 근사하게 잡거나 또는 랜덤 한 벡터로 설정한다.
(2 단계) s=1,2,… 에 대하여 bs+1을 다음과 같이 업데이트한다.
bs=Abs−1‖
(3 단계) \|b_{s} - b_{s-1}\|_2< \epsilon(또는 \|b_{s} - b_{s-1}\|_2/\|b_{s-1}\|_2<\epsilon )인 경우 알고리즘을 종료하고 b_{s}을 최종 벡터로 선정한다. 아닌 경우 b_{s-1} \longleftarrow b_{s}로 설정하고 (2 단계)로 돌아간다.
A의 고유값을 절대값에 대하여 내림차순으로 정렬했다고 하자.
|\lambda_1| \geq |\lambda_2| \geq \cdots \geq |\lambda_n|
그리고 이에 대응하는 고유 벡터를 v_1, v_2, \ldots, v_n이라 하자.
위 알고리즘을 통해 얻은 벡터 b에 대하여 b^tAb/b^tb가 우리가 찾고자 하는 \lambda_1이 된다.
Power Iteration 알고리즘은 다음을 만족할 때 수렴한다고 알려져 있다.
(조건 1) |\lambda_1| > |\lambda_2|
(조건 2) 즉, b_0 = c_1v_1+c_2v_2+\cdots+ c_nv_n이라 할 때 c_1\neq 0이어야 한다.
(조건 1)은 가장 큰 고유값이 두 번째 고유값보다 같지 않고 확실하게 커야 한다는 것이다. 그리고 (조건 2)는 초기 벡터 b_0가 v_1의 방향 성분을 가져야 한다는 것이다. 수렴성에 대한 증명이 궁금한 분들은 위키 백과를 참고하면 된다.
아니 그냥 대각화 방법이든 뭐든 해서
정확한 고유값을 계산하면 되지
뭐 하러 Power Iteration 알고리즘을 쓰는가?
라고 할 수 있는데 주어진 행렬의 사이즈가 큰 경우 정확한 고유값을 계산하기 위한 계산량이 엄청나다. 하지만 Power Iteration 알고리즘은 행렬과 벡터 곱에 대한 연산만 들어가 계산량이 적다. 즉, 약간의 정확성을 포기한 대신 계산량이 적은 방법으로 고유값의 근사값을 계산해 낼 수 있다. 다만 Power Iteration 알고리즘은 \lambda_1, \lambda_2에 따라서 수렴 속도가 느려질 수 있다.
b. PLSR 모형 추정 방법
PLSR에서는 n\times p 설명 변수 행렬 X, n\times q 반응 변수 행렬 Y가 다음과 같은 구조로 이루어져 있다고 가정한다.
X=TW^t+E, Y = UQ^t+F \tag{1.5}
여기서 E, F는 오차항을 나타내는 행렬이다. 간단히 말하자면 PLSR은 X와 Y를 잘 근사하는(잘 설명하는) 새로운 변수 행렬 T, U를 찾는 것이다.
그렇다면 X, Y를 어떻게 연결할까? 그것은 바로 다음과 같이 T, U의 상관관계를 설명하는 벡터 z를 찾는 것이다.
U = Tz\tag{1.6}
그렇다면 Y의 추정 행렬 \hat{Y}은 다음과 같이 계산한다.
\hat{Y} = UQ^t = TzQ^t \tag{1.7}
PLSR 회귀 추정 방법은 (1.5)에서 새로운 변수 행렬 T, U를 찾고 (1.7)의 회귀 계수 벡터를 구하는 단계로 이루어진다.
(1) T, U 찾기
(1.5)에서 T, U를 찾는 알고리즘은 다음과 같다.
Algorithm 1.
선형 결합 개수 k를 선택하고 l=0로 설정한다.
(1 단계) 한계 오차 \epsilon>0을 설정하고, 임의의 l = 1, \ldots, q 에 대하여 u_0 = \tilde{y}_l으로 세팅한다.
(2 단계) s=1, 2, \ldots에 대하여 다음을 계산한다.
\begin{align} w_s &= X^tu_{s-1}/ \| X^tu_{s-1} \|_2 \\ t_s &= Xw_s \\ q_s &= Y^tw_s / \|Y^tw_s \|_2 \\ u_s &= Yq_s \end{align}
(3 단계) \|t_s - t_{s-1}\|_2/\|t_{s-1} \| > \epsilon 인 경우 $t_{s-1} \longleftarrow t_s$로 설정하고 (2 단계)로 돌아간다.
(4 단계) \|t_s - t_{s-1}\|_2/\|t_{s-1} \| \leq \epsilon 경우 t_{l+1}=t_s, w_{l+1} = w_s, u_{l+1}=u_s, q_{l+1} = q_s으로 하고 X := X-t_{l+1}w_{l+1}^t, Y:= Y-u_{l+1}q_{l+1}^t로 세팅한 뒤 (2 단계)로 돌아간다. 만약 l+1 = k라면 알고리즘을 종료한다.
(2) 회귀 계수 벡터 계산
앞의 알고리즘 결과로 우리는 다음을 얻은 것이다.
T = (t_1\;\; t_2 \;\; \cdots \;\; t_k), W = (w_1\;\; w_2 \;\;\cdots \;\; w_k), \\ U = (u_1 \;\; u_2 \;\; \cdots \;\; u_k), Q = (q_1 \;\; q_2 \;\; \cdots \;\; q_k)
이때 T = XW인 것을 알 수 있다.
이제 (1.6)의 관계를 이용하여 z를 계산한다.
z = (T^tT)^{-1}T^tU\tag{1.8}
(1.5)와 (1.7)을 이용하여 \hat{Y} 다시 써보면 다음과 같다.
\hat{Y} = TzQ^t = XWzQ^t \tag{1.9}
이제 회귀 계수 벡터 b=WzQ^t로 설정한다.
c. PLSR 추정 방법의 이해
Algorithm 1에서 (2 단계)에서 구한 w_s의 의미를 알아보기 위해 w_s를 다시 써보자.
\begin{align} w_s &= X^tu_{s-1}/ \| X^tu_{s-1} \|_2 \\ &= X^tYq_{s-1} / \| X^tYq_{s-1} \|_2 \\ &= X^tYY^tt_{s-1}/\|X^tYY^tt_{s-1} \|_2 \\ &= X^tYY^tXw_{s-1} / \| X^tYY^tXw_{s-1} \| \end{align}\tag{1.10}
설명의 편의를 위해 w=w_s로 하겠다. (1.10)은 앞에서 다룬 Power Iteration 알고리즘에서 b=w, A=X^tYY^tX인 경우의 업데이트 규칙과 동일하다. 즉, w는 X^tYY^tX의 가장 큰 고유값에 대응하는 고유 벡터로 볼 수 있는 것이다. 즉,
\DeclareMathOperator*{\argmax}{arg\,max} w = \argmax_{\|p\|_2=1}p^tX^tYY^tp
(1.3)에서 PLSR은 선형 결합의 분산 \text{Var}(Xw)을 크게하고 반응 변수와의 상관성을 나타내는 \text{Corr}(Y, Xw)^t \text{Corr}(Y, Xw)을 크게 하는 선형 결합을 찾는다고 했었다. 이에 대한 부분을 수학적으로 증명해 보자. 먼저 w를 잘 정리해 보면 다음과 같다.
\DeclareMathOperator*{\argmax}{arg\,max} \begin{align}w &= \argmax_{\|p\|_2=1}p^tX^tYY^tp \\ &= \argmax_{\|p\|_2=1} (Y^tXp)^t(Y^tXp) \\ &= \argmax_{\|p\|_2=1} \text{Cov}(Y, Xp)^t \text{Cov}(Y, Xp) \\ &= \argmax_{\|p\|_2=1} \left ( \text{Var}(Y)^{\frac{1}{2}} \text{Corr}(Y, Xp) \text{Var}(Xp)^{\frac{1}{2}} \right ) ^t \left ( \text{Var}(Y)^{\frac{1}{2}} \text{Corr}(Y, Xp) \text{Var}(Xp)^{\frac{1}{2}} \right ) \\ &= \argmax_{\|p\|_2=1} \text{Var}(Xp) \text{Corr}(Y, Xp)^t \text{Var}(Y) \text{Corr}(Y, Xp) \end{align}
위 전개 과정을 통해 w는
\text{Var}(Xw), \;\; \text{Corr}(Y, Xw)^t \text{Var}(Y) \text{Corr}(Y, Xw)
을 크게하는 것을 알 수 있다. 일단 분산을 최대화하는 선형 결합을 찾는 것은 알았다. 하지만 두 번째 식에서 반응 변수의 분산 \text{Var}(Y)가 문제가 된다. 만약 반응 변수가 한개(q=1)이라면 반응 변수의 분산은 양의 실수가 되어 생략할 수 있어서 바로 \text{Corr}(Y, Xw)^t \text{Corr}(Y, Xw)를 크게 한다는 결론을 얻을 수 있지만 반응 변수가 여러 개인 경우(q>1)에는 간단하지 않다.
두 번째 식을 최대화하는 것의 의미를 차근차근 살펴보자. 먼저 p(w) = \text{Corr}(Y, Xw)라 하자. 그리고 \text{Var}(Y)을 양정치 행렬이라 가정하고 이것의 고유값을 내림차순으로 정렬한 것을 \lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_n이라 하고 이에 대응하는 고유 벡터를 v_i라 하자.
\text{Var}(Y)은 대칭행렬이므로 고유 벡터들은 Orthogonal Basis를 형성한다. 그에 따라 p(w)를 다음과 같이 표현할 수 있다.
p(w) = a_1(w) v_1 + a_2(w)v_2+\cdots a_n(w)v_n
우리가 원하는 결론은 p(w)^t\text{Var}(Y) p(w)을 크게 하는 것이 p(w)^tp(w)를 크게하는 것과 어떤 관계인지를 알아내는 것이다.
p(w)^t\text{Var}(Y) p(w) = \sum_{i=1}^n a_i(w)^2\lambda_i \leq \lambda_1 \sum_{i=1}^na_i(w)^2 = \lambda_1 p(w)^tp(w)
\text{Var}(Y)은 양정치 행렬이므로 정리에 의하여 \lambda_1>0이고 이를 양변에 나누어주면
p(w)^t\text{Var}(Y) p(w)/\lambda_1 \leq p(w)^tp(w)
위 식이 의미하는 것은 p(w)^t\text{Var}(Y) p(w)/\lambda_1은 p(w)^tp(w)의 하한이며 \lambda_1은 양수이므로 하한을 크게하면 p(w)^tp(w) = \text{Corr}(Y, Xw)^t\text{Corr}(Y, Xw)도 크게 할 수 있다는 것이다.
요약하면 Algorithm 1의 (2 단계)에서 구한 w를 이용한 선형 결합 Xw는 그 자체 분산과 반응 변수와의 상관성을 크게 해주는 설명 변수의 선형 결합이라는 것이다.
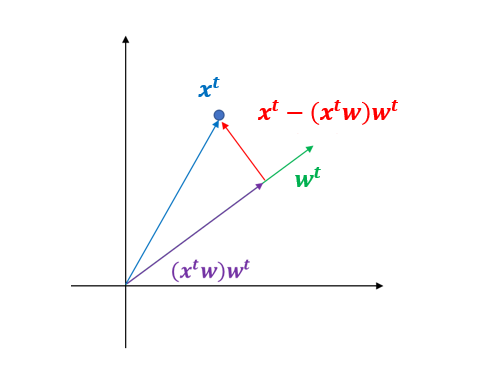
이번엔 Algorithm 1의 (4 단계)에서 X - tw^t의 의미는 X에서 t로 설명하지 못하는 부분을 의미한다. 이를 이해하기 위해 X-tw^t를 살펴보면
\begin{align} X-tw^t &= X-(Xw)w^t \\ &= \begin{pmatrix} x_1^t \\ x_2^t \\ \vdots \\ x_n^t \end{pmatrix} - \begin{pmatrix} (x_1^tw)\cdot w^t \\ (x_2^t w)\cdot w^t \\ \vdots \\ (x_n^t w) \cdot w^t \end{pmatrix} = \begin{pmatrix} x_1 - (x_1^t w) w^t \\ x_2 - (x_2^t w) w^t \\ \vdots \\ x_n - (x_n^t w) w^t \end{pmatrix} \end{align}
여기서 x_i^t = (x_{i1}, x_{i2}, \ldots, x_{ip}) 즉, X의 i번째 행 벡터이다. 위 행렬에서 i번째 행은 x_i - (x_i^tw) w^t이며 이는 관측치와 관측치를 w 축 방향으로 투영시킨 부분을 뺀 부분(아래 그림에서 빨간 벡터)이며 이는 관측치의 w 축 방향의 성분으로 설명하지 못하는 일종의 잔차와 같은 것이다
(x_i^tw)w^t로 써야 쉽게 해석되는데 이것을 x_i^t(ww^t) 식으로 써버리면 외적(Outer Product)이 포함된 것처럼 보여서 해석이 어렵다.
PLSR은 이전 선형 결합 t_{j-1}이 설명하지 못하는 부분을 잘 설명하는 선형 결합 t_{j}을 찾게 되며 이러한 반복적인 과정을 통해 얻어지는 선형 결합 t_1, t_2, \ldots, t_k 사이에 상관성이 매우 낮게 된다. 따라서 PLSR은 설명 변수의 다중 공선성 문제도 해결할 수 있는 것이다.
이와 동일한 원리로 Y - uq^t 도 Y에서 반응 변수의 선형 결합 u로 설명하지 못하는 부분을 의미한다.
PLSR은 X, Y에서 설명하지 못하는 부분에 대해서 반복적으로 새로운 선형 결합을 찾게 되는데 그러한 의미에서 부분을 나타내는 Partial이 붙게 된 것이다.
4) 고려 사항
a. 선형 결합의 개수
선형 결합의 개수는 이론적인 방법은 없고 Elbow Plot 등을 이용하여 주관적으로 선택한다. 예를 들어 선형 결합 개수를 x축, 그에 대응하는 성능 지표(예 : MSE)를 그려서 그에 대한 증가분(또는 감소분)이 급격하게 줄어든 지점을 최종 선형 결합의 개수로 정할 수 있다.
b. 반응 변수에 범주형이 포함된 경우
PLSR은 범주형 반응 변수도 처리할 수 있다고 알려져 있다. 만약 반응 변수 중에 범주형이 있다고 하면 One-Hot Encoding으로 변환하여 PLSR 모형을 추정할 수도 있다. 즉, 범주형 반응 변수의 범주 개수만큼 더미 변수를 만든다(보통 같으면 범주 개수보다 하나 더 적은 더미 변수를 생성하지만 여기서는 아니다).
예를 들어 y의 범주가 3개라면 다음과 같이 더미 변수 3개(D1, D2, D3)를 생성한 뒤 앞에서 다룬 것과 동일하게 PLSR을 수행하면 된다.
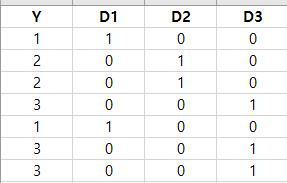
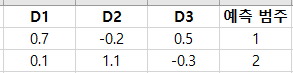
물론 D1, D2, D3에 대한 예측값은 음수이거나 1보다 큰 값이 나올 수 있다. 이때 각 관측치 별로 더미 변수에 대한 예측값이 큰 쪽에 해당하는 범주를 예측 범주로 정한다. 예를 들어 예측값이 D1 = 0.7, D2 = -0.2, D3=0.5가 나왔다면 D1의 값이 가장 크므로 이에 대응하는 범주 1로 예측하게 되는 것이다. 아래 표는 이러한 예를 나타낸 것이다.
2. 파이썬 구현
이번엔 PLSR 알고리즘을 파이썬으로 구현해 보자. 여기서는 반응 변수가 2개 이상인 경우만을 다루며 하나인 경우의 알고리즘은 위키 백과를 참고하기 바란다.
아래 코드에서 PLSR은 PLSR 모형을 추정하는 클래스이다. 이 클래스는 선형 결합 개수(n_components)를 지정하고 fit 메서드를 통하여 PLSR 모형을 추정한다. predict는 설명 변수들의 행렬을 받아서 예측을 수행한다. 앞에서 다룬 PLSR 모형 추정 방법을 그대로 코드로 옮긴 것이므로 이해하는데 어려움은 없을 것 같다.
import numpy as np class PLSR: def __init__(self, n_components): self.n_components = n_components self.x_mean = None ## 설명 변수 평균 벡터 self.y_mean = None ## 반응 변수 평균 벡터 self.W = None ## W self.T = None ## T self.Q = None ## Q self.U = None ## U self.coef = None ## 회귀 계수 행렬 def fit(self, X, y, tolerance=1e-5, max_iter=50): n_loop = self.n_components W = [] T = [] Q = [] U = [] ## mean-centering x_mean = np.mean(X, axis=0) self.x_mean = x_mean X_bar = X - x_mean y_mean = np.mean(y, axis=0) self.y_mean = y_mean y_bar = y - y_mean ## get components for i in range(n_loop): u = y_bar[:, 0].reshape(-1, 1) Xu_norm = np.linalg.norm(X_bar.T @ u ) w = X_bar.T @ u / Xu_norm t = X_bar @ w yu_norm = np.linalg.norm(y_bar.T @ t ) q = y_bar.T @ t / yu_norm u = y_bar @ q iter_num = 1 while iter_num <= max_iter: Xu_norm = np.linalg.norm(X_bar.T @ u ) next_w = X_bar.T @ u / Xu_norm next_t = X_bar @ next_w yu_norm = np.linalg.norm(y_bar.T @ next_t ) next_q = y_bar.T @ next_t / yu_norm next_u = y_bar @ next_q if np.linalg.norm(next_t-t) < tolerance: break else: t = next_t u = next_u iter_num += 1 W.append(next_w.flatten().tolist()) T.append(next_t.flatten().tolist()) Q.append(next_q.flatten().tolist()) U.append(next_u.flatten().tolist()) X_bar = X_bar - next_t@next_w.T y_bar = y_bar - next_u@next_q.T self.W = np.array(W).T self.T = np.array(T).T self.Q = np.array(Q).T self.U = np.array(U).T W = self.W T = self.T U = self.U Q = self.Q TtT_inv = np.linalg.inv(T.T @ T) z = TtT_inv @ T.T @ U self.coef = W @ z @ Q.T return self def predict(self, X): X_bar = X - self.x_mean y = X_bar @ self.coef + self.y_mean return y
3. 예제
이제 실제 데이터를 이용하여 앞에서 구현한 클래스를 시험해 보자. 비교 대상은 Scikit-Learn에서 제공하는 PLSRegression 클래스이다. 여기서는 연속형 반응 변수와 범주형 반응 변수에 대한 데이터를 이용하여 성능을 비교해보고자 한다.
1) 연속형 반응 변수
연속형 반응 변수가 여러 개인 마땅한 데이터가 없어서 Scikit-Learn 문서에서 예제로 사용한 샘플 데이터를 이용하여 (학습) 성능을 비교해보고자 한다. 여기서는 선형 결합의 개수를 2개로 고정했다. 성능 지표는 MSE를 사용했다.
from sklearn.cross_decomposition import PLSRegression X = [[0., 0., 1.], [1.,0.,0.], [2.,2.,2.], [2.,5.,4.]] Y = [[0.1, -0.2], [0.9, 1.1], [6.2, 5.9], [11.9, 12.3]] X = np.array(X) Y = np.array(Y) n_components = 2 my_plsr = PLSR(n_components=n_components).fit(X, Y) sk_plsr = PLSRegression(n_components=n_components).fit(X, Y) my_pred = my_plsr.predict(X) sk_pred = sk_plsr.predict(X) def get_mse(y, pred): return np.mean(np.square(y-pred)) print('내꺼 :', get_mse(Y, my_pred)) print('sklearn :', get_mse(Y, sk_pred))

결과를 확인해 보니 내가 구현한 게 좀 더 성능이 좋았다.
2) 범주형 변수
붓꽃 데이터(Iris)를 이용하여 반응 변수가 범주형인 경우 앞에서 구현한 PLSR의 성능을 Scikit-Learn의 PLSRegression과 비교해보고자 한다.
먼저 붓꽃 데이터를 불러오고 이를 One-Hot Encoding으로 변환한다.
from sklearn.datasets import load_iris iris = load_iris() X = iris.data y = iris.target num = np.unique(y) dummy_y = np.eye(len(num))[y] ## y를 One-Hot encoding으로 변환 print(dummy_y)
[[1. 0. 0.] [1. 0. 0.] [1. 0. 0.] [1. 0. 0.] [1. 0. 0.] '''중략''' [0. 0. 1.] [0. 0. 1.] [0. 0. 1.] [0. 0. 1.]]
이제 성능을 비교해 볼 시간이다. 성능은 정분류율로 계산했다.
n_components = 2 my_plsr = PLSR(n_components=n_components).fit(X, dummy_y) sk_plsr = PLSRegression(n_components=n_components).fit(X, dummy_y) my_pred = my_plsr.predict(X) my_pred = np.argmax(my_pred, axis=1) ## 높은 값을 갖는 더미 칼럼 인덱스를 예측 범주로 변환 sk_pred = sk_plsr.predict(X) sk_pred = np.argmax(sk_pred, axis=1) ## 높은 값을 갖는 더미 칼럼 인덱스를 예측 범주로 변환 def get_accuracy(y, pred): return np.mean(np.square(y==pred)) print('내꺼 :', get_accuracy(y, my_pred)) print('sklearn :', get_accuracy(y, sk_pred))

여기서도 내가 구현한 게 좀 더 좋은 학습 성능을 보였다. ㄷㄷ;
4. 장단점
PLSR의 장단점은 다음과 같다.
- 장점 -
a. 데이터 개수보다 더 많은 변수를 가진 고차원 데이터를 차원 축소를 통하여 더 효율적으로 회귀 모형을 만들 수 있다.
b. 다중 공선성을 처리할 수 있다.
PLSR은 다중공선성이 있는 설명 변수를 상관성이 낮은 새로운 변수로 변환하고 이를 회귀 모형에 사용하므로 다중공선성 문제를 해결할 수 있다.
c. 연속형, 범주형 반응 변수를 모두 고려할 수 있다.
d. 구현이 쉽다.
PLSR은 구현이 쉽다.
- 단점 -
a. 이해하기가 어렵다.
PLSR에서 T, U를 찾는 알고리즘이 그렇게 직관적이지 않고 이를 이해하려면 수학적 지식을 많이 필요로 한다.
b. 계산량이 많다.
PLSR에서 T, U를 찾는 알고리즘의 속도가 느리며 행렬 계산이 다수 포함되어 있어 사이즈가 큰 행렬에 대해서는 계산량 측면에서 불리하다.
c. 이상치에 민감하다.
PLSR은 데이터의 이상치가 포함되어 있으면 추정값을 신뢰할 수 없게 된다.
d. 해석이 어렵다.
설명 변수가 많다면 PLSR에서 추정한 회귀 계수 벡터에 대한 해석이 어렵게 된다.
e. 설명 변수 선형 결합의 개수를 정하는 데 있어 이론적인 근거는 없고 Elbow Plot을 이용하여 주관적으로 판단해야 한다.
'통계 > 머신러닝' 카테고리의 다른 글
| 40. 인자 분석(Factor Analysis)에 대해서 알아보자 with Python (0) | 2023.05.03 |
|---|---|
| 39. 정준 상관 분석(Canonical Correlation Analysis)에 대해서 알아보자 with Python (6) | 2023.04.23 |
| 37. 주성분 분석(Principal Component Analysis : PCA)에 대해서 알아보자 with Python (0) | 2023.04.01 |
| 36. Reduced Rank Regression(RRR)에 대해서 알아보자 with Python (2) | 2023.03.16 |
| 35. Spline Regression에 대해서 알아보자 with Python (2) | 2023.02.19 |





댓글