이번 포스팅에서는 머신러닝 예측 모형 간 성능을 시각적으로 비교해 볼 수 있는 방법으로 ROC(Receiver Operating Characteristic) 곡선과 AUC(Area Under the Cuve)에 대한 개념을 알아보고 이를 파이썬(Python)으로 구현해보고자 한다. 이 포스팅은 민감도(Sensitivity, 또는 재현율 Recall)와 특이도(Specificity)에 대해서 안다고 가정한다. 민감도와 특이도에 대해서 궁금하신 분들은 여기에서 민감도와 특이도 파트를 참고하기 바란다.
- 목차 -
1. ROC(Receiver Operating Characteristic) 곡선
1. ROC(Receiver Operating Characteristic) 곡선
1) 정의
ROC(Receiver Operating Characteristic) 곡선은 2 클래스 분류 모형에서 여러 절단값(Threshold)에서의 민감도와 특이도의 관계를 나타내는 곡선을 말한다.
위 정의를 하나하나 살펴보자.
a. 파헤치기
먼저 데이터 $(x_i, y_i), i=1, \ldots, n$이 주어졌다고 하자. 이때 $x_i\in \mathbb{R}^p, y_i \in \{0, 1\}$이다. 이러한 데이터를 이용하여 분류 모형 $f$를 학습했다고 하자. 이 모형은 $x_i$가 주어진 경우 $Y_i=1$인 조건부 확률을 예측한다. 즉,
$$f(x_i) = \hat{P}(Y_i=1|x_i)$$
ROC 곡선을 이야기할 때에는 2 클래스 분류 문제로 한정한다. 그리고 이 문제를 해결하는 예측 모형은 특정 클래스($Y_i=1$)의 조건부 확률을 계산할 수 있어야 한다(예: 로지스틱 회귀 모형). 그리고 상수 $c\in [0, 1]$가 주어졌을 때 새로운 데이터 $x$에 대해서 다음과 같은 규칙에 의해 클래스 $y$를 예측한다.
$$y = \begin{cases} 1 & \text{if } \hat{P}(Y=1|x) > c \\ 0 & \text{o.w.} \end{cases}$$
이처럼 특정 데이터를 1로 분류할지 말지를 결정하는 상수 $c$를 절단값이라 하겠다. 주어진 절단값을 이용하여 분류를 하게 되면 아래와 같이 2X2 혼동행렬(Confusion Matrix)을 만들 수 있다.

이때 민감도 $Senc(c)$와 특이도 $Spec(c)$는 다음과 같다.
$$\begin{align}Sens(c) &= \frac{TP}{TP+FN} \\ Spec(c) &= \frac{TN}{FP+TN} \end{align}$$
이때 절단값에 따라서 1로 예측되는 클래스(그에 따라 0으로 예측되는 클래스) 개수가 달라진다. 따라서 여러 절단값에 따라서 민감도와 특이도가 달라지기 때문에 민감도와 특이도를 $c$의 함수로 표시할 수 있다.
또한 여러 절단값에 따른 민감도와 특이도의 관계를 그림으로 표현할 수 있는데 아래 그림과 같이 민감도와 1-특이도를 계산하여 2차원 평면에 그릴 수 있다. 왜 민감도와 특이도가 아닌 민감도와 1-특이도의 관계인지는 아래에서 설명한다.

b. ROC 곡선의 성질
ROC 곡선의 몇 가지 성질을 알아보자. 만약 절단값을 작게 할수록 예측 라벨이 1인 경우의 수가 늘어날지언정 감소하진 않을 것이다. 하지만 실제 라벨이 1인 경우와 0인 경우의 데이터 숫자는 고정이므로 다음의 성질을 알 수 있다.
성질 1
$$c_1<c_2 \Rightarrow Sens(c_1)\geq Sens(c_2) \;\;\text{ and} \;\; 1-Spec(c_1) \geq 1-Spec(c_2) \tag{1}$$
즉 민감도와 1-특이도는 절단값 $c$에 대하여 단조 감소함수라는 것이다. 만약 1-특이도가 아닌 특이도였다면 단조 감소가 아닌 단조 증가가 되어 민감도의 변화 방향과 반대가 된다. 따라서 절단값에 따른 변화의 방향을 맞춰주어 시각적인 해석을 좀 더 쉽게 하기 위하여 민감도와 1-특이도의 관계를 그리게 된 것이다.
이번엔 새로운 데이터에 대해서 $y$의 예측값 $\hat{y}$이 1이 될 확률을 1-절단값 즉, $1-c$로 하여 랜덤 하게 예측한다고 해보자(이러한 모형을 Random Model 또는 Random Guessing이라고 한다). 이를 달리 말하면 확률 변수 $\hat{Y}$은 성공 확률이 $1-c$인 베르누이 분포를 따른다는 것과 같다.
$$\hat{Y} \sim \text{Ber}(1-c), c\in [0, 1]$$
또한 $\hat{Y}$은 실제 라벨 $Y$와 관계없이 순수히 확률만을 가지고 예측하므로 $\hat{Y}$와 $Y$는 독립이다. 즉,
$$P(\hat{Y}=1|Y=1) = P(\hat{Y}=1|Y=0) = P(\hat{Y}=1)=1-c$$
위 등식에서 첫 번째 확률 $P(\hat{Y}=1|Y=1)$을 예측값과 실제 데이터로 추정한 것이 민감도이고 두 번째 확률 $P(\hat{Y}=1|Y=0)$은 예측값과 실제 데이터로 추정한 1-특이도가 된다. 따라서 Random Model인 경우에는 민감도=1-특이도=$k$라고 간주할 수 있으며 $k$는 $1-c$로 설정한다는 것이다. 이를 통해 다음을 알 수 있다.
성질 2
만약 Random Model이라면 ROC 곡선은 $y=x$이라고 간주한다.
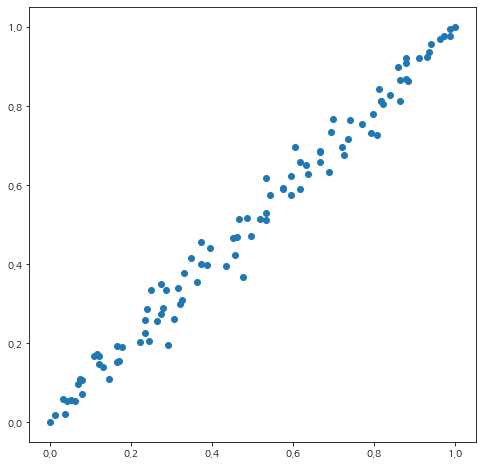
실제로 Random Model을 이용하여 ROC 곡선을 그려보면 정확하게 $y=x$는 아니고 아래와 같이 $y=x$를 중심으로 약간 퍼져있다.
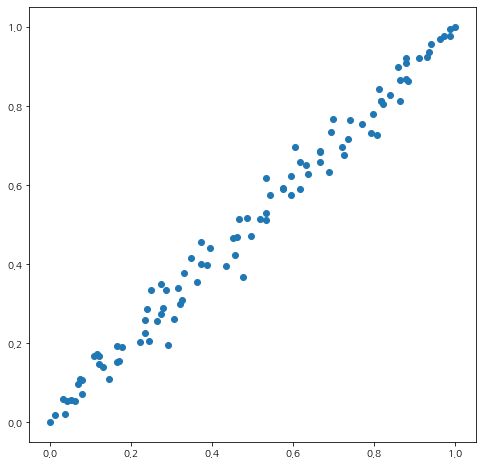
c. ROC 곡선 그리기
학습된 예측 모형 $f$와 민감도와 특이도를 계산할 데이터가 주어졌다고 해보자. 또한 절단값 리스트는 0부터 1 사이의 격자점(e.g. 0, 0.01, $ldots, 0.99, 1)이라고 하자. 이때 ROC 곡선 그리는 방법은 다음과 같다.
단계 1) 각 격자점에 대하여 학습된 예측 모형의 민감도와 특이도를 계산한다.
단계 2) 1-특이도를 x축에 민감도를 y축으로 하여 곡선을 그린다.
단계 1)~2)를 거치면 아래와 같은 곡선을 얻을 수 있다.
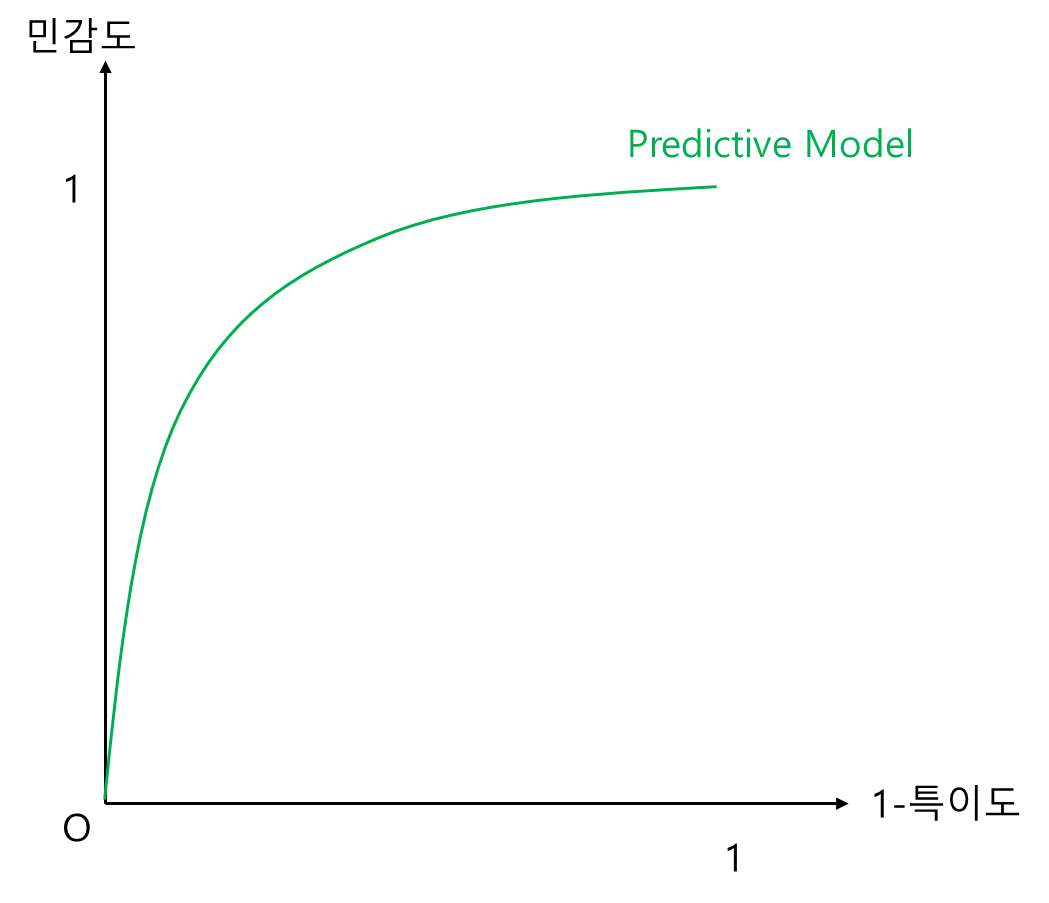
그렇다면 ROC 곡선은 왜 그리는 걸까? 단순히 특이도와 민감도의 관계를 보기 위한 것도 있지만 여러 모형의 성능을 시각적으로 비교하기 위해 ROC 곡선을 사용한다.
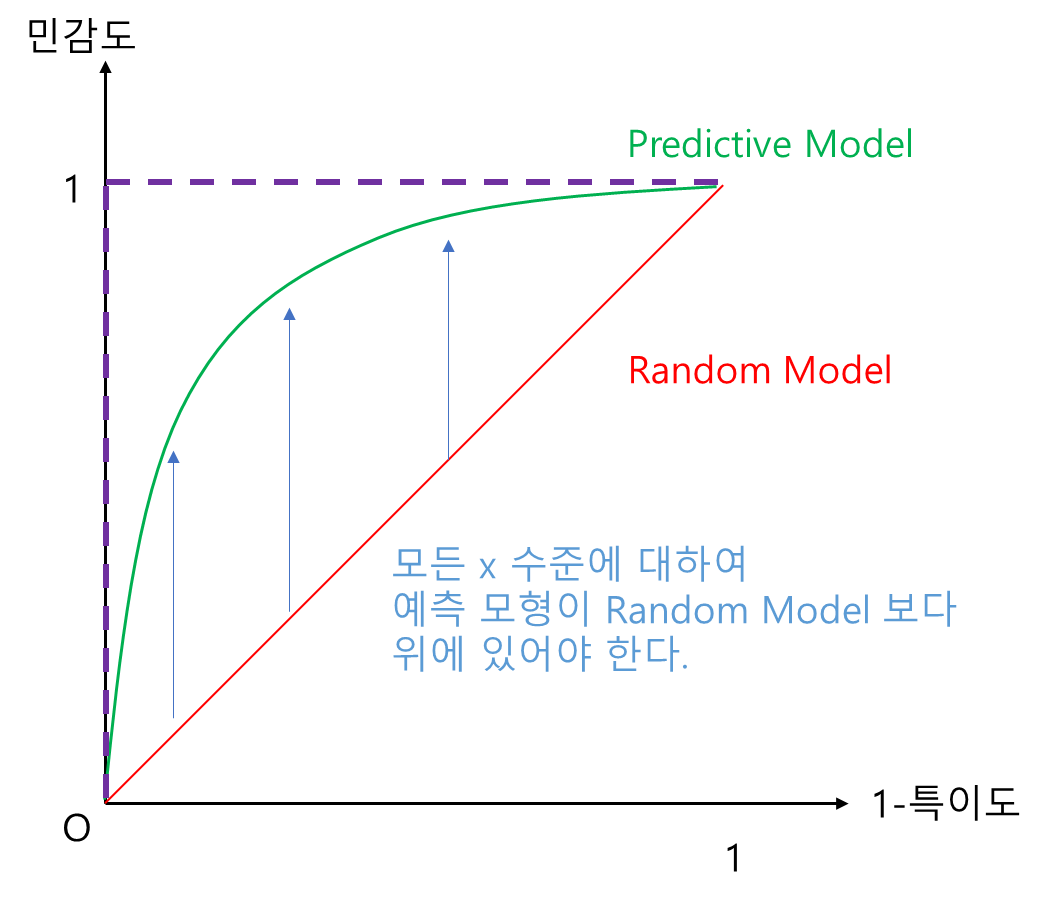
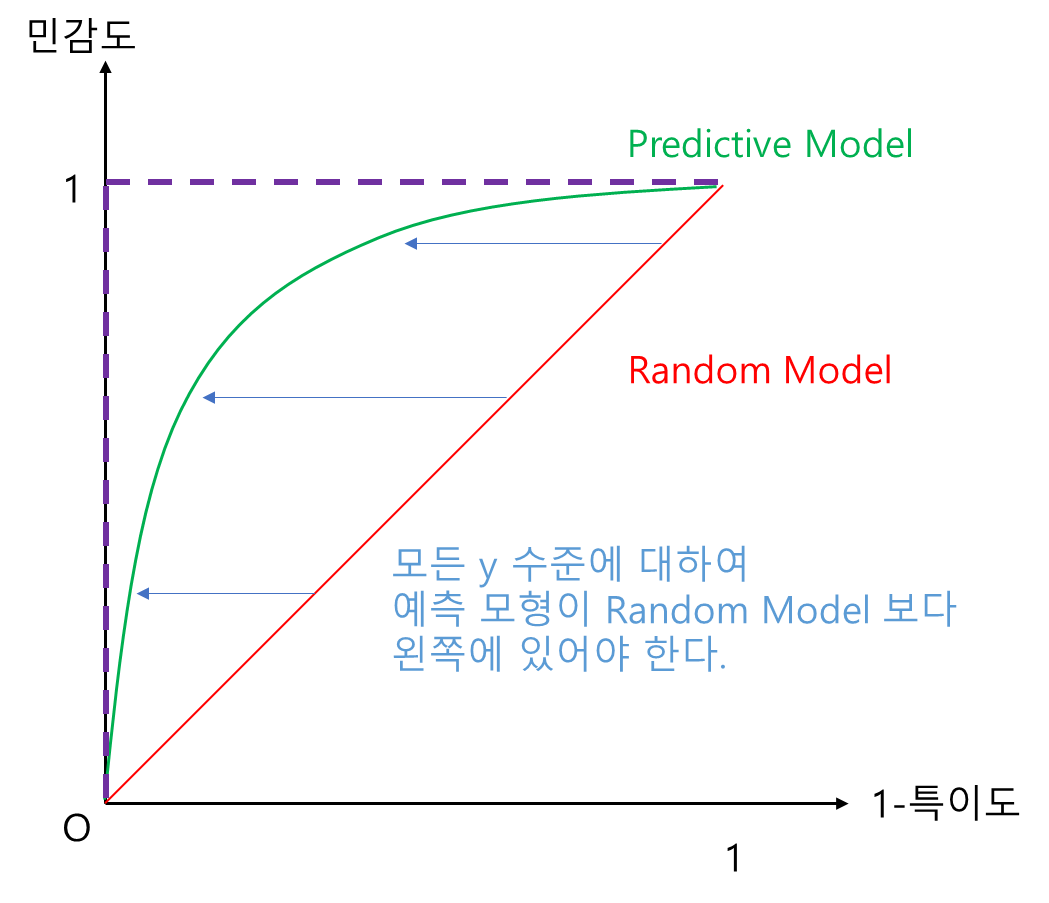
그림과 함께 살펴보자. 일단 예측 모형(초록선)은 당연히 Random Model(빨간 선) 보다는 좋아야 할 것이다. 즉, 예측 모형은 모든 x(1-특이도) 수준에 대하여 Random Model 보다 y값(민감도)이 커야 하며 다시 말해 y축 방향으로 Random Model 보다 위에 있어야 한다(왼쪽 그림). 또한 모든 y(민감도) 수준에 대하여 x값 (1-특이도) 값은 작을수록 좋으며 다시 말해 Random Model 보다 x축 방향으로 왼쪽에 있어야 한다(오른쪽 그림). 또한 민감도와 1-특이도는 모두 0과 1 사이 값을 가지므로 보라색 점선과 같은 경계를 가진다. 이 경계가 가장 Perfect 한 모형이 된다. 쉽게 말해 ROC 곡선이 좌상단으로 쏠려 있을수록 좋은 것이다.
지금까지 얘기한 것은 ROC 곡선을 통하여 예측 모형의 최소 자격 요건을 만족하는지(Random Model보다 좋은지) 살펴본 것이다. ROC 곡선은 여러 예측 모형 간 비교도 가능하게 해 준다. 앞에서 살펴본 내용과 본질은 같다. 모든 x(1-특이도) 수준에서 곡선이 좌상단에 쏠려 있는 모형이 더 좋은 것이다. 즉, 아래 그림에서 예측 모형 A가 B보다 성능이 좋다고 할 수 있다.
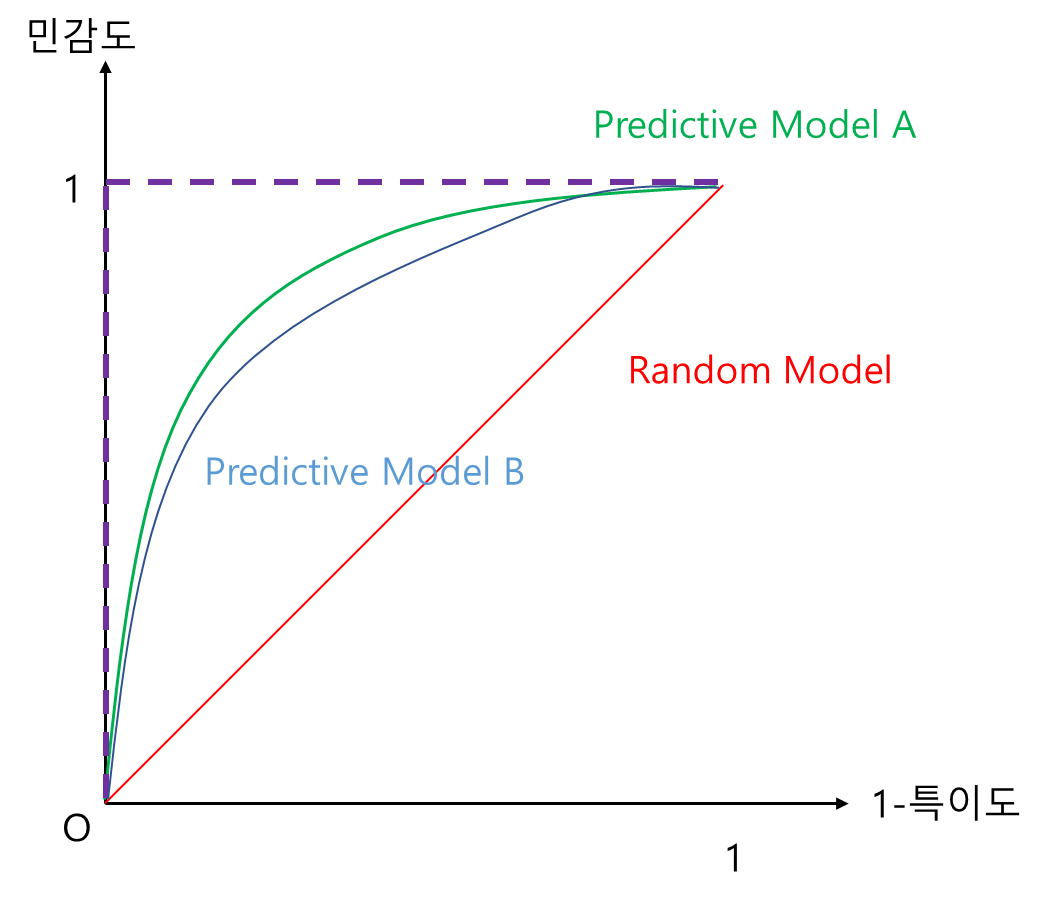
또 하나의 이유가 있다. 바로 최적 절단값을 선택하는데 ROC 곡선이 도움을 줄 수도 있기 때문이다. 만약 어떤 문제에서 최소한으로 만족해야 하는 민감도가 0.9라고 해보자. 이때 아래 그림과 같이 주어진 학습 모형에 대하여 y값을 0.9로 하는 x축과 평행한 직선을 그어 ROC 곡선과 만나는 지점에서의 절단값이 0.5라고 한다면 절단값을 0.5 이하로 하면 최소 민감도를 해당 모형에 대해서는 만족할 수 있는 것이다. 최소 1-특이도를 만족하는 절단값을 찾는 것도 이와 비슷하다.

2) 파이썬 예제
이제 파이썬(Python)을 이용하여 ROC 곡선을 그려보자. 먼저 아래 get_roc_xy 함수는 특정 절단값 $c$에서 민감도와 1-특이도 값을 리턴한다. 이 함수는 Random Model(random_guess=True)에 대한 결과도 리턴한다.
def get_roc_xy(y_true, c, clf=None, random_guess=False, seed=100):
def get_sensitivity(y_true, y_pred):
denom = np.sum(y_true == 1)
num = np.sum((y_pred == 1)&(y_true==1))
return num/denom
def get_specificity(y_true, y_pred):
denom = np.sum(y_true == 0)
num = np.sum((y_pred == 0)&(y_true==0))
return num/denom
if not random_guess:
assert clf is not None
assert hasattr(clf, 'predict_proba') ## 분류기는 확률을 예측할 수 있어야 한다.
y_pred = np.where(clf.predict_proba(X)[:, 1]>c, 1, 0)
y = get_sensitivity(y_true, y_pred)
x = 1-get_specificity(y_true, y_pred)
else:
np.random.seed(seed)
y_pred = np.random.choice([0, 1], len(y_true), p=[c, 1-c])
y = get_sensitivity(y_true, y_pred)
x = 1-get_specificity(y_true, y_pred)
return x, y
여기서는 2 클래스 데이터로 유방암 데이터를 사용하겠다.
import matplotlib.pyplot as plt
from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.ensemble import AdaBoostClassifier
bc = load_breast_cancer()
X = bc.data
y = bc.target
먼저 앞에서 살펴봤던 Random Model의 ROC 곡선을 그려보자.
## Random Model의 ROC 곡선
x_data = []
y_data = []
for i, c in enumerate(np.linspace(0, 1, 101)):
x_coord, y_coord = get_roc_xy(y, c, random_guess=True, seed=i)
x_data.append(x_coord)
y_data.append(y_coord)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(x_data, y_data)
plt.show()
이번엔 로지스틱 회귀와 AdaBoost를 이용하여 분류 성능을 살펴보자.
## 분류기 학습
clf1 = LogisticRegression(solver="liblinear", random_state=0).fit(X, y)
clf2 = AdaBoostClassifier(random_state=0).fit(X, y)
## Random Model의 ROC 곡선
x_data1 = []
y_data1 = []
x_data2 = []
y_data2 = []
for i, c in enumerate(np.linspace(0, 1, 101)):
x_coord1, y_coord1 = get_roc_xy(y, c, clf=clf1)
x_data1.append(x_coord1)
y_data1.append(y_coord1)
x_coord2, y_coord2 = get_roc_xy(y, c, clf=clf2)
x_data2.append(x_coord2)
y_data2.append(y_coord2)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.plot(x_data1, y_data1, label='LR')
ax.plot(x_data2, y_data2, label='AdaBoost')
ax.plot([0, 1], [0, 1], color='red', label='Random Model')
ax.legend()
plt.show()
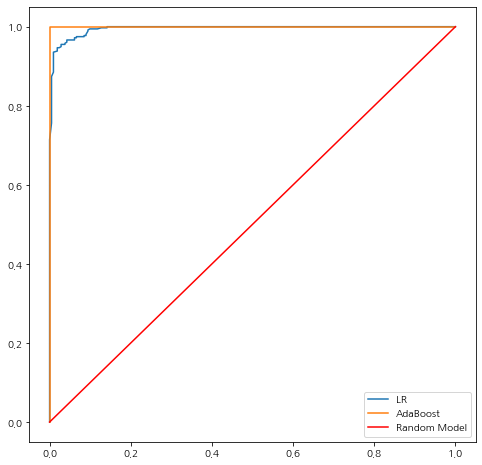
코드를 실행하고 시각화 결과를 살펴보니 AdaBoost가 좋은 것을 알 수 있다.
Scikit-Learn을 이용하여 ROC 곡선을 그릴 수도 있다. roc_curve를 이용하면 된다. 이때 실제값과 예측 확률을 넣어주면 True Positve Rate와 False Positive Rate 그리고 절단값을 리턴한다. 이때 True Positve Rate와 False Positive Rate은 각각 민감도와 1-특이도이다.
from sklearn.metrics import roc_curve
score1 = clf1.predict_proba(X)[:, 1]
score2 = clf2.predict_proba(X)[:, 1]
fpr1, tpr1, _ = roc_curve(y, score1)
fpr2, tpr2, _ = roc_curve(y, score2)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.plot(fpr1, tpr1, label='LR')
ax.plot(fpr2, tpr2, label='AdaBoost')
ax.plot([0, 1], [0, 1], color='red', label='Random Model')
ax.legend()
plt.show()
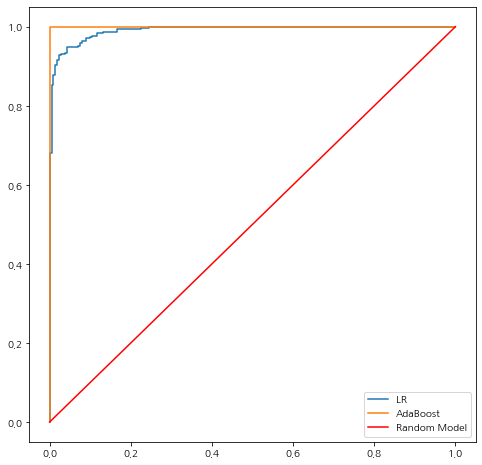
3) 장단점
ROC 곡선의 장단점은 다음과 같다.
- 장점 -
a. 모형 클래스의 상관없이 그릴 수 있으며 그에 따라 모형 간 성능 비교를 시각적으로 알아볼 수 있다.
b. 2 분류 모형의 민감도(Sensitivity 또는 Recall)과 특이도의 관계를 시각적으로 알아볼 수 있다.
c. 구현이 쉽다.
절단값에 따른 확률을 이용하여 예측 라벨을 구한 다음 민감도와 1-특이도만 계산하면 되므로 구현이 간단하다.
d. 불균형 클래스(Imbalance) 문제에서 최적 절단값 선택을 시각적으로 도와줄 수 있다.
- 단점 -
a. 하나의 모형이 다른 모형보다 모든 구간에서 높지 않은 경우 해석에 문제가 생긴다.
예를 들어 Model1과 Model2가 아래와 같이 크로스가 발생한 경우에는 어느 하나가 다른 하나보다 좌상단 쪽으로 쏠려있지 않아 성능 비교가 어렵다. 이 경우 아래에서 다룰 AUC를 사용하면 크로스 문제를 해결할 수 있다.
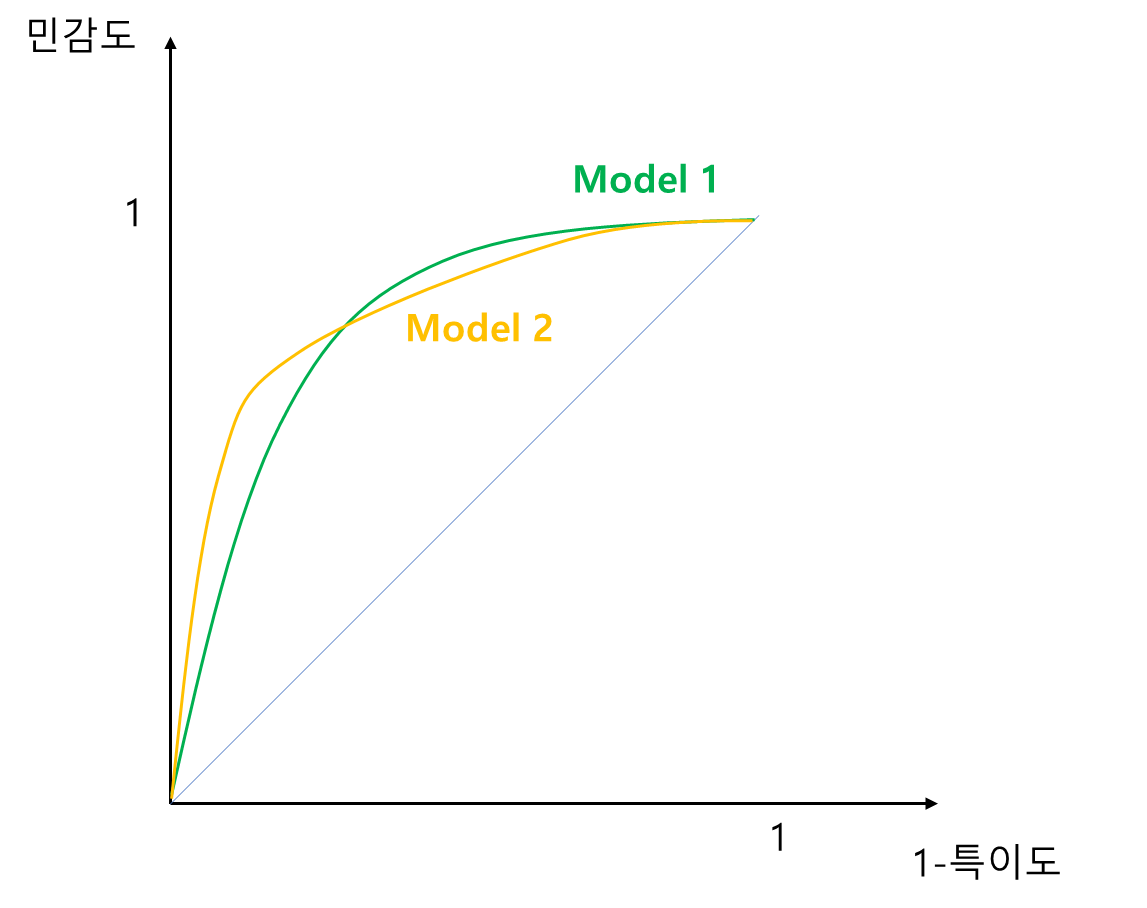
b. 멀티 클래스 분류 문제에서는 사용하기 어렵다.
c. 불균형 클래스 문제에서 잘못된 판단을 이끌어낼 수도 있다.
d. 머신러닝을 잘 모르는 사람들한테 직관적으로 와닿지 않을 수 있다.
2. AUC(Area Under the Cuve)
1) 정의
ROC 곡선의 아래 면적을 AUC라 한다.
a. 파헤치기
AUC 또한 2 분류 예측 모형의 성능을 시각적으로 비교하는데 쓰일 수 있다. ROC 곡선에서 곡선이 좌상단으로 쏠려있을수록 좋다고 했다. 이를 면적 관점에서 본다면 곡선 아래 면적이 클수록 좋은 모형이 된다. 즉, AUC 값이 클수록 좋은 것이다. 예를 들어 아래 그림에서 Model1이 Model2 보다 면적이 크므로 성능이 더 좋은 모형이 된다.

면적의 크기를 비교한다는 점 때문에 두 ROC 곡선이 크로스한다고 해도 모형 성능 비교가 가능하다. 이게 AUC만이 갖는 특징이다. 예를 들어 아래 그림과 같이 두 모형의 ROC 곡선이 크로스한다고 해도 면적의 크기는 비교할 수 있는 것이다.

ROC 곡선 아래의 면적이므로 AUC는 0과 1 사이의 값을 가지며 Random Model의 경우는 0.5가 된다. 따라서 기본적으로 0.5보다는 커야 예측 모형이 제 구실을 할 수 있다고 본다.
2) 파이썬 예제
이번엔 파이썬으로 AUC를 계산하는 함수를 만들어보자. 아래 get_auc 함수는 민감도를 y, 1-특이도를 x좌표로 하여 AUC를 계산한다. 곡선 아래 면적은 점과 점 사이는 직선으로 간주하여 사다리꼴 넓이 공식을 사용하여 계산한다.
def get_auc(x, y):
x = np.array(x)
y = np.array(y)
y = y[np.argsort(x)]
x = np.sort(x)
return (y[1:] + y[:-1]).dot(x[1:]-x[:-1])*0.5
이번에도 유방암 데이터를 이용하여 로지스틱 회귀와 AdaBoost 모형을 학습시키고 AUC를 각각 계산해 보았다.
## 분류기 학습
clf1 = LogisticRegression(solver="liblinear", random_state=0).fit(X, y)
clf2 = AdaBoostClassifier(random_state=0).fit(X, y)
## Random Model의 ROC 곡선
x_data1 = []
y_data1 = []
x_data2 = []
y_data2 = []
for i, c in enumerate(np.linspace(0, 1, 101)):
x_coord1, y_coord1 = get_roc_xy(y, c, clf=clf1)
x_data1.append(x_coord1)
y_data1.append(y_coord1)
x_coord2, y_coord2 = get_roc_xy(y, c, clf=clf2)
x_data2.append(x_coord2)
y_data2.append(y_coord2)
print('LR', get_auc(x_data1, y_data1))
print('AdaBoost', get_auc(x_data2, y_data2))

AdaBoost 모형의 AUC가 1이 나왔다. ㄷㄷ;; 이 데이터에 대해서는 퍼펙트 성능을 보여주었다.
AUC는 Scikit-Learn에서 roc_auc_score 또는 auc를 이용하여 계산할 수 있다. 이때 roc_auc_score은 실제 라벨과 예측 확률을 넣어주고 auc는 1-특이도와 민감도로 이루어진 배열을 계산하면 된다.
from sklearn.metrics import roc_auc_score, auc
score1 = clf1.predict_proba(X)[:, 1]
score2 = clf2.predict_proba(X)[:, 1]
print('roc_auc_score')
print('LR', roc_auc_score(y, score1))
print('AdaBoost', roc_auc_score(y, score2))
print()
print('auc')
print('LR', auc(x_data1, y_data1))
print('AdaBoost', auc(x_data2, y_data2))
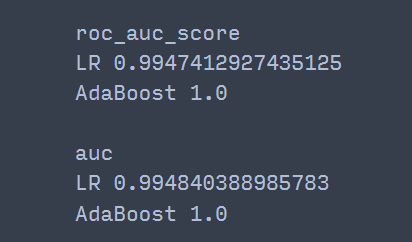
AdaBoost의 AUC는 직접 구현한 것과 똑같았고 로지스틱 회귀에 대해서는 직접 구현한 것뿐만 아니라 auc와 roc_auc_score 함수 간에도 약간의 차이를 보였다.
3) 장단점
AUC의 장단점은 다음과 같다.
- 장점 -
a. ROC 곡선과 마찬가지로 모형 클래스에 상관없이 계산 가능하며 그에 따라 여러 모형 간 성능 비교 지표로 활용할 수 있다.
b. ROC 곡선의 크로스 문제를 해결할 수 있다.
c. 구현이 쉽다.
- 단점 -
a. 최적 절단값에 대한 정보를 주지 못한다.
b. 민감도와 특이도의 관계를 알려주지 않는다.
'통계 > 머신러닝' 카테고리의 다른 글
| 36. Reduced Rank Regression(RRR)에 대해서 알아보자 with Python (2) | 2023.03.16 |
|---|---|
| 35. Spline Regression에 대해서 알아보자 with Python (2) | 2023.02.19 |
| 33. 클러스터링(군집화) 평가 지표 Calinski-Harabasz index, Davies-Bouldin index, Rand Index에 대해서 알아보자 with Python (1) | 2023.01.22 |
| 32. Gain Chart와 Lift Chart에 대해서 알아보자 with Python (0) | 2023.01.17 |
| 31. 지도 학습 모형 성능 지표에 대해서 알아보자 with Python (2) | 2023.01.13 |





댓글