이번 포스팅에서는 고유값 분해(Eigen Decomposition)의 일반화 버전인 특이값 분해(Singular Value Decomposition : SVD)에 대한 내용을 정리해 보았다. SVD의 개념과 Numpy 모듈을 이용하여 SVD 표현식을 구하는 방법을 소개한다.
만약 고유값 분해에 대해서 모르는 분이 있다면 아래 포스팅을 보고오기 바란다. 그래야 이번 포스팅도 이해하기 쉽다.
고유값과 고유 벡터 그리고 고유값 분해(Eigen Decomposition)에 대해서 알아보자 (feat. Numpy)
Singular Value Decomposition(SVD)
a. 정의
$\text{rank}(A)=r$인 $m\times n$ 행렬 $A$에 대하여 다음의 표현식을 만족하는 $m\times m$ Orthogonal 행렬 $P$과 $n\times n$ Orthogonal 행렬 $Q$ 그리고 대각 원소가 양수인 $r\times r$ 대각행렬 $D$가 존재한다.
$$A = P\begin{pmatrix} D_{r\times r} & 0_{r\times (n-r)} \\ 0_{(m-r)\times r } & 0_{(m-r)\times (n-r)} \end{pmatrix}Q^t \tag{1}$$
주어진 행렬 $A$를 (1)과 같이 분해하는 것을 특이값 분해 Singular Value Decomposition(SVD)이라 한다.
고유값 분해와는 달리 $A$의 SVD는 항상 존재한다는 것을 알 수 있다(고유값 분해는 대각화 가능한 행렬만 가능하다). SVD가 존재한다는 것을 알았으니 $P, D, Q$를 찾는 방법을 알아보자. 여기서는 몇 가지 선형 대수 정리를 증명 없이 이용하여 찾아보고자 한다.
필요한 선형 대수 정리들
아래 정리에서 언급하는 행렬은 모두 실수 원소를 갖는 행렬이다.
정리 1
$n\times n$ 대칭 행렬 $A$는 $n$개의 Orthgonal 고유 벡터를 갖는다.
정리 2
임의의 $m\times n$ 행렬 $A$에 대하여
(1) $\text{rank}(A) = \text{rank}(A^t)$
(2) $\text{rank}(A^tA) = \text{rank}(A)$
정리 3
반 양정치 행렬(Positive Semi-definite)는 음이 아닌 고유값을 갖는다.
정리 4
대칭 행렬 $A$가 $\text{rank}(A)=r$이라면 $r$개의 0이 아닌 고유값을 갖는다.
이제 $\text{rank}(A)=r$인 $m \times n$ 행렬 $A$가 주어진 경우 SVD 방법을 알아보자.
SVD 방법
$D$ 찾기
$A^tA$의 0이 아닌 $r$개의 고유값 $\lambda_1, \ldots, \lambda_r$을 찾는다. $A^tA$는 대칭 행렬이고 정리 2에 의하여 $\text{rank}(A^tA) = \text{rank}(A)=r$이다. 따라서 정리 4에 의하여 이러한 $r$개의 고유값을 찾을 수 있다. 그리고 $s_i = \sqrt{\lambda_i}$라 하고($A^tA$는 반 양정치 행렬이므로 정리 4에 의하여 가능하다) 크기 순으로 정렬되어 있다고 하자 즉,
$$s_1\geq s_2 \geq \cdots \geq s_r$$
이다. 이때 $s_i$를 특이값(Singular Value)이라 한다.
이제 $D$를 다음과 같이 설정한다.
$$D=\begin{pmatrix} s_1 &0 &\cdots & 0 \\ 0& s_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & s_r \end{pmatrix}$$
$Q$ 찾기
$Q$의 칼럼 벡터는 $A^tA$의 고유 벡터로 정한다. $A^tA$는 $n\times n$ 대칭 행렬이므로 정리 1에 의하여 $n$개의 Orthogonal 고유 벡터가 있으며 이에 따라 $Q$는 $n\times n$ Orthogonal 행렬이 된다. 이때 $Q$의 처음 $r$개의 칼럼 벡터는 $\lambda = s_i^2$에 대응하는 고유 벡터 $q_i$로 하며 나머지 $n-r$개 칼럼 벡터는 고유값 0에 대한 고유 벡터로 (순서 상관없이) 채우게 된다.
$$Q = \begin{pmatrix} q_1 \cdots q_r \cdots q_n \end{pmatrix}$$
$P$ 찾기
$P$의 처음 $r$개의 칼럼 벡터 $p_i(1\leq i \leq r)$를 다음과 같이 설정한다.
$$p_i = s_i^{-1}Aq_i\tag{2}$$
이렇게 설정하면 $p_i$는 $AA^t$의 0이 아닌 고유값의 대응하는 고유 벡터가 된다. 이때 고유값은 $A_tA$의 0이 아닌 고유값 $\lambda_i$에 정확히 대응된다. 이때 정리 2를 이용하면
$$\text{rank}(AA^t) = \text{rank}(A^t) = \text{rank}(A) = \text{rank}(A^tA)$$
임을 알 수 있다. 따라서 대칭 행렬 $AA^t$는 정리 4에 의하여 $r$개의 0이 아닌 고유값을 가지며 이에 대응하는 고유 벡터는 정확히 $P$의 처음 $r$개의 칼럼 벡터가 된다. 정리 1에 의하여 $n$개의 Orthogonal 고유 벡터가 있으므로 $P$의 나머지 $n-r$개 칼럼은 $AA^t$의 고유값 0에 대응하는 $n-r$개 고유 벡터로 순서 상관없이 채우게 된다($AA^t$ 또한 반 양정치 행렬이므로 정리 4에 의하여 고유값이 0이 아니라면 가능한 고유값은 0 밖에 없는 것이다). $P$ 또한 Orthgonal이 된다.
그렇다면 이렇게 찾은 $P, D, Q$를 이용하면 (1)을 만족하는지 확인해야 한다. (1)을 보이는 것은 결국 다음을 보이는 것과 같다.
$$P^tAQ = \begin{pmatrix} D_{r\times r} & 0_{r\times (n-r)} \\ 0_{(m-r)\times r } & 0_{(m-r)\times (n-r)} \end{pmatrix}$$
먼저 $P=(P_1, P_2), Q = (Q_1, Q_2)$라 하자. 여기서 $P_1, Q_2$는 각각 $P, Q$의 처음 $r$개의 칼럼 벡터로 이루어진 분할 행렬이다.
$$Q^tA^tAQ = \begin{pmatrix} Q_1^tA^tAQ_1 & Q_1^tA^tAQ_2 \\ Q_2^tA^tAQ_1 & Q_2^tA^tAQ_2 \end{pmatrix} = \begin{pmatrix} D_{r\times r}^2 & 0_{r\times (n-r)} \\ 0_{(m-r)\times r } & 0_{(m-r)\times (n-r)} \end{pmatrix}$$
이때 마지막 등식은 $Q$의 정의로부터 도출된 것이다. 위 식에 의하여 $Q_1^tA^tAQ_1=D^2$임을 알 수 있다. 또한 $(AQ_2)^tAQ_2 = Q_2^tA^tAQ_2 = 0$이며 자기 자신의 내적이 0이면 자기 자신도 0이므로 $AQ_2=0$이다. (2)를 행렬로 표현하면 $P_1 = AQ_1D^{-1}$이고 이를 이용하면 다음을 알 수 있다.
$$P_1^t = D^{-1}Q_1^tA^t, \;\; AQ_1 = P_1D$$
마지막으로 $P$는 Orthogonal 칼럼 벡터로 이루어져 있으므로 $P_1^tP_2 = 0$이다.
이러한 사실을 이용하여 $P^tAQ$를 계산해 보자.
$$\begin{align} P^tAQ &= \begin{pmatrix} P_1^tAQ_1 & P_1^tAQ_2 \\ P_2^tAQ_1 & P_2^tAQ_2 \end{pmatrix}\\ &= \begin{pmatrix} D^{-1}Q_1^tA^tAQ_1 & P_1^t0 \\ P_2^tP_1D & P_2^t0 \end{pmatrix} \\ &= \begin{pmatrix} D^{-1}D^2 & 0 \\ (P_1^tP_2)^tD & 0 \end{pmatrix} = \begin{pmatrix} D_{r\times r} & 0_{r\times (n-r)} \\ 0_{(m-r)\times r } & 0_{(m-r)\times (n-r)} \end{pmatrix} \end{align}$$
b. 기하학적 의미와 필요성
- SVD 표현식의 의미 -
$A$가 다음과 같이 특이값 분해 표현식을 갖는다고 해보자.
$$A = PD'Q^t \tag{3}$$
여기서
$$D' = \begin{pmatrix} D_{r\times r} & 0_{r\times (n-r)} \\ 0_{(m-r)\times r } & 0_{(m-r)\times (n-r)} \end{pmatrix}$$
이다.
이때 위 표현식의 기하학적인 의미를 살펴보고자 한다.
정리 5
Orthogonal 행렬 $P_{n\times n}$는 길이와 내적을 보존한다. 즉,
(1) $\|Px\|_2 = \|x\|_2, \;\; \forall \; x\in \mathbb{R}^n$
(2) $(Px)^t(Py) = x^ty \;\; \forall \; x, y\in \mathbb{R}^n $
여기서 $\|x\|_2$는 Euclidean Norm이다.
내적을 보존한다는 것은 (길이가 보존되기 때문에) 두 벡터 사이의 각도를 보존한다는 것이며 이는 Orthogonal 행렬이 회전(Rotation) 또는 반사(Refection) 행렬이라는 것을 의미한다. 다시 말해 $Px$는 주어진 벡터 $x$를 회전 또는 반사(대칭 변환)시키는 것이 된다.
이때 $Px$가 기존 $x$와의 각도를 $\theta_P$라 할 때, $\theta_P$를 $P$와 $x$로 표현해 보자.
$$\begin{align} x^t(Px) &= \| x\|_2\| Px\|_2\cos\theta_P \\ &= \|x\|_2\|x\|_2\cos\theta_P = \|x\|_2^2\cos\theta_P \\ &\Rightarrow \theta_P = \cos^{-1}\left ( \frac{x^tPx}{\| x\|_2^2} \right) \end{align}$$
아래 그림은 2차원 상에서 Orthogonal 행렬 $P$의 성질을 나타낸 것이다.
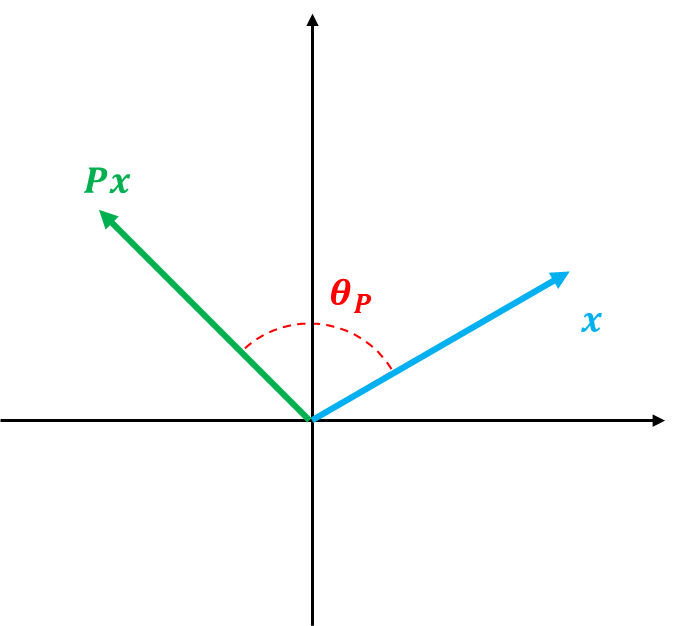
대각 행렬은 주어진 벡터를 개별 축 방향으로 대각 원소가 1보다 크다면 늘이고 0가 1 사이라면 줄인다(특이값 분해에서는 대각 행렬 원소가 음이 아닌 실수라는 것을 기억하자).

위 내용을 바탕으로 특이값 분해 표현식을 통해 $Ax$는 주어진 벡터 $x$를 $Q^t$를 통해 회전(또는 반사)시키고($Q$가 Orthogonal이면 $Q^t$도 Orthogonal이다) $D'$을 통해 개별 축으로 축소 또는 확대시키며 확대되며 다시 $P$를 통해 회전(또는 반사)시키게 된다.

- 특이값의 의미 -
특이값 $s^2$은 $A^tA$의 고유값 중 하나이다. 이에 대응되는 고유 벡터를 $v$($\|v\|_2 = 1$)라 할 때 다음을 알 수 있다.
$$s^2 = s^2\|v\|_2^2 = s^2 v^tv = v^t(s^2v) = v^t(A^tAv) = (Av)^t(Av) = \| Av\|_2^2$$
$s \geq 0$이므로 $s =\|Av \|_2$가 된다.
또한 $A$의 $i$번째 행 벡터를 $\tilde{a}_i^t = (a_{i1}, \ldots, a_{in})$라 할 때
$$\|Av \|_2 = \sqrt{\sum_{i=1}^n(\tilde{a}_i^tv)^2 }$$
이다. 이를 통해 특이값 $s$는 $A$의 행 벡터를 $v$ 위로 투영시킨 정사영 길이 제곱합의 제곱근이라는 것이다.
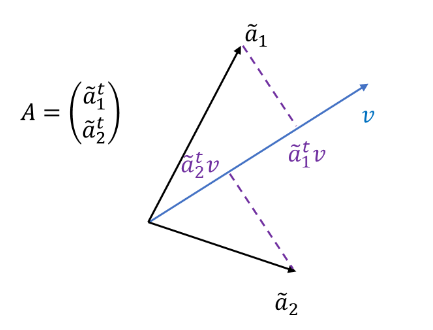
- SVD가 왜 필요한가? -
만약 $D'$에서 대각 원소를 처음 $k$($\leq r$)개만 취한 대각 행렬을 $D_k'$, 처음 $k$개의 칼럼을 $P$에서 뽑아낸 것을 $P_k^t$ 그리고 $Q^t$에서 처음 $k$개 행을 뽑아낸 행렬을 $Q^t_k$라 하자. 그리고 $A_k = P_kD_k'Q_k^t$라 하자.
$A_k$는 $A$의 특이값 분해로부터 얻을 수 있는데 $A_k$는 특별한 성질이 있다. 바로 $\text{rank}(A_k) = k$이며 $A_k$는 $A$를 Frobenius Norm($L_2$ Norm에 대해서도 성립한다)에 대해서 가장 잘 근사하는 rank-$k$인 행렬이라는 것이다. 즉,
$$\|A-A_k \|_F \leq \| A-B\|_F, \;\; \forall \; B\in \mathbb{R}^{m\times n} \text{with rank}(B)=k$$
즉, 특이값 분해(SVD)를 이용하면 주어진 $A$를 잘 근사하는 일종의 차원이 축소된 low-rank $A_k$를 찾을 수 있고 이는 행렬의 압축(예 원본 이미지를 최대한 유지하면서 파일 크기를 압축), 노이즈 제거(Denoising) 그리고 행렬의 결측값 추정(Matrix Completion) 등에 활용된다.
c. 예제
$$A = \begin{pmatrix} 3 & 2 & 2 \\ 2 & 3 & -2 \end{pmatrix}$$
인 경우 특이값 분해를 해보자.
$D'$ 찾기
먼저 (3)에서 $D'$을 찾아야 한다. $A^tA$에서 0이 아닌 고유값을 찾아야 한다. 즉, 아래 행렬의 Determinant를 계산해야 한다.
$$A^tA -\lambda I = \begin{pmatrix} 13-\lambda & 12 & 2 \\ 12 & 13 -\lambda & -2 \\ 2 & -2 & 8-\lambda \end{pmatrix}$$
계산하면 $\lambda = 25, 9, 0$을 얻을 수 있다. 이때 0이 아닌 고유값은 25, 9이며 이들의 양의 제곱근 즉, 특이값은 5, 3이 된다. 따라서 $2\times 3$ 행렬 $D'$는 다음과 같다.
$$D' = \begin{pmatrix} 5 & 0 & 0 \\ 0&3&0 \end{pmatrix}$$
$Q$ 찾기
고유값 25, 3, 0에 대응하는 고유 벡터를 찾고 이들을 칼럼 벡터로 하는 것을 $Q$로 설정하면 된다. 25에 대응하는 고유 벡터 $v_{25} = (x, y, z)$라 할 때
$$(A^tA-25I)v_{25} = \begin{pmatrix} -12 & 12 & 2 \\ 12 & -12 & -2 \\ 2 & -2 & -17 \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = 0_{3\times 1}$$
을 풀어야 한다. 위 식을 정리하면
$$-6x + 6y + z = 0, \;\; x-y-17z = 0$$
이 되고 이를 통해 $x=y, z=0$인 것을 알 수 있다. 따라서 임의의 실수 $c$에 대하여 $c \cdot (1, 1, 0)$이 고유 벡터가 될 수 있으며 길이가 1인 고유 벡터 $v_{25} = (1/\sqrt{2}, 1/\sqrt{2}, 0) $로 한다. 비슷한 방법으로 9에 대응하는 고유 벡터 $v_9 = (1/\sqrt{18}, -1/\sqrt{18}, 4/\sqrt{18})$이다. 0에 대응하는 고유 벡터 $v_0 = (2/3, -2/3, -1/3)$이다. 이 3개의 벡터를 칼럼으로 하는 행렬을 $Q$로 설정한다.
$$Q = \begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{18} & 2/3 \\ 1/\sqrt{2} & -1/\sqrt{18} & -2/3 \\ 0 & 4/\sqrt{18} & -1/3 \end{pmatrix}$$
$P$ 찾기
특이값 5, 3에 대응하는 고유 벡터 $v_{25}, v_9$을 이용하여 다음의 벡터 $p_1, p_2$를 아래와 같이 계산한다.
$$\begin{align}p_1 &= 5^{-1}Av_{25} = (1/\sqrt{2}, 1/\sqrt{2}) ,\\ p_2 &= 3^{-1} Av_9 = (1/\sqrt{2}, -1/\sqrt{2}) \end{align}$$
이제 $p_1, p_2$를 칼럼으로 하는 행렬을 $P$로 설정한다.
$$P = \begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} \\ 1/\sqrt{2} & -1/\sqrt{2} \end{pmatrix}$$
필요한 건 모두 찾았다. $A$의 특이값 분해는 다음과 같다.
$$\begin{align}A &= PD'Q^t\\ &= \begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} \\ 1/\sqrt{2} & -1/\sqrt{2} \end{pmatrix} \begin{pmatrix} 5 & 0 & 0 \\ 0&3&0 \end{pmatrix} \begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{18} & 2/3 \\ 1/\sqrt{2} & -1/\sqrt{18} & -2/3 \\ 0 & 4/\sqrt{18} & -1/3 \end{pmatrix}^t \end{align}$$
d. 파이썬 예제
이번엔 앞에서 살펴본 예제를 파이썬으로 풀어보자. 아래 코드는 앞의 예제를 각 스텝 별로 구현한 것이다.
import numpy as np
A = np.array([[3,2,2], [2, 3, -2]]) ## 주어진 행렬
eigen_values, eigen_vectors = np.linalg.eig(A.T @ A) ## AtA의 고유값과 고유 벡터
## 아주 작은 수는 0으로 설정
tol = 1e-10
eigen_values[np.abs(eigen_values)<tol] = 0
eigen_vectors[np.abs(eigen_vectors)<tol] = 0
## 특이값 계산
non_zero_eig = eigen_values[eigen_values>0]
singular_values = np.sqrt(non_zero_eig)
singular_values = singular_values[np.argsort(-singular_values)]
Q = eigen_vectors[:, np.argsort(-eigen_values)] ## Q계산
## D', P 계산
D_prime = np.zeros_like(A)
ps = []
for i, s in enumerate(singular_values):
D_prime[i, i] = s
p = s**(-1)*(A@Q[:, i])
ps.append(p)
P = np.c_[ps].T
print('P')
print(P)
print()
print('D_prime')
print(D_prime)
print('Q')
print(Q)
print()
print(P@D_prime@Q.T) ## A와 같다.

Numpy에서는 np.linalg.svd를 이용하여 특이값 분해를 쉽게 할 수 있다. np.linalg.svd는 행렬을 입력으로 전달받으며 순서대로 $P$, 특이값(Singular Value) 배열 그리고 $Q^t$를 반환한다($Q$가 아니라는 점에 주목하자). 아래 코드를 실행하면 위 결과와 동일하게 나온다.
A = np.array([[3,2,2], [2, 3, -2]]) ## 주어진 행렬
P, D, Q_t = np.linalg.svd(A)
tol = 1e-10
Q_t[np.abs(Q_t)<tol] = 0
D_prime = np.c_[np.diag(D), np.array([0, 0])]
print('P')
print(P)
print()
print('D_prime')
print(D_prime)
print('Q')
print(Q_t.T)
print()
print(P@D_prime@Q_t) ## A와 같다.'통계 > 기타' 카테고리의 다른 글
| 고유값과 고유 벡터 그리고 고유값 분해(Eigen Decomposition)에 대해서 알아보자 (feat. Numpy) (2) | 2023.03.04 |
|---|---|
| ANOVA(Analysis of Variance, 분산분석)에 대해서 알아보자. (7) | 2022.12.06 |
| 통계학이란 무엇인가? (0) | 2022.11.07 |
| 가중치를 활용한 통계량을 알아보자. 가중 평균(Weighted Mean), 가중 상관계수(Weighted Correlation), 가중 분위수 (Weighted Quantile) (2) | 2022.09.25 |
| Profile Likelihood 란 무엇인가?! (408) | 2022.04.30 |





댓글