이번 포스팅에서는 고유값과 고유 벡터에 대해서 간단히 알아본 뒤 고유값 분해(Eigen Decomposition)에 대해서 알아보고자 한다.
고유값 분해(Eigen Decomposition)
고유값 분해를 이야기하기 전에 간단하게 고유값(Eigenvalue)과 고유벡터(Eigenvector)의 정의를 알아보자. 본 포스팅에서 나오는 행렬은 모두 실수 값을 원소로 한다.
1. 고유값(Eigenvalue)과 고유벡터(Eigenvector)
a. 정의
$n\times n$ 정방행렬 $A$가 주어졌을 때 다음을 만족하는 0이 아닌 $n$차원 벡터 $v$가 있다고 하자.
$$Av = \lambda v, \;\; \lambda \in \mathbb{C}\tag{1}$$
이때 $\lambda$를 고유값(Eigenvalue), $v$를 $\lambda$에 대응하는 고유벡터(Eigenvector)라고 한다.
b. 기하학적인 의미
대칭 행렬(Symmetric Matrix)의 고유값은 실수라는 사실이 알려져 있다. 이를 이용하면 고유값과 고유벡터에 대한 기하학적인 해석을 해볼 수 있다.
$n\times n$ 정방행렬 $A$가 주어졌다고 해보자. 이때 특정 $n$차원 벡터 $v$를 $A$를 이용한 변환 결과가, 즉 $Av$가 원 벡터 $v$를 같은 방향 또는 반대 방향으로 길이를 늘이거나 줄였다면(길이가 그대로인 경우도 포함) 늘리거나 축소시킨 정도가 고유값이 되고 그에 대응하는 벡터가 고유벡터가 되는 것이다(아래 그림 참고).
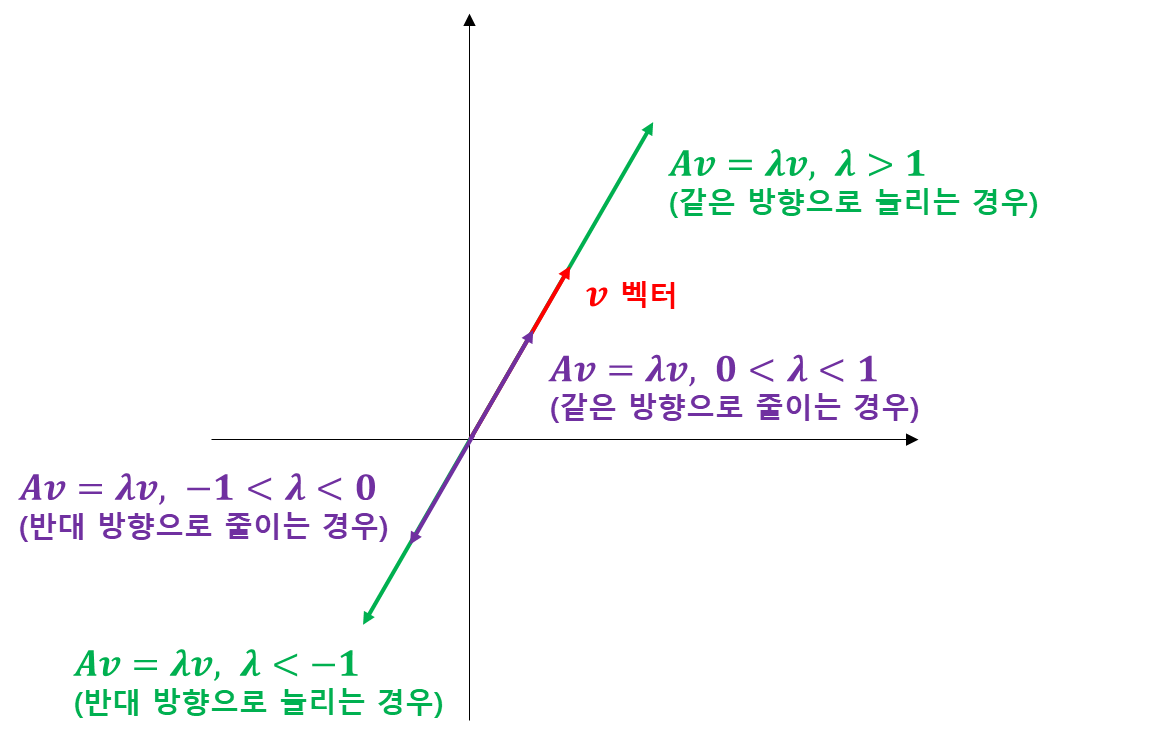
만약 주어진 대칭 행렬이 반 양정치 행렬(Positive Semi Definite Matrix 또는 Non-negative Definite Matrix)라면 모든 고유값은 음이 아닌 실수라는 사실이 알려져 있다.
이때 대칭 행렬에 반 양정치 행렬이라는 조건이 추가되면 고유값은 또 다른 기하학적 의미를 갖는다. $A$를 반 양정치 대칭 행렬이라고 하자. 이때 $\lambda(>0)$을 $A$의 한 고유값이라고 하자. 이에 대응되는 고유 벡터를 $v$라 하자. 주어진 벡터 $x = (x_1, \ldots, x_n)$에 대한 Euclidean Norm은 다음과 같이 정의한다.
$$\|x\|_2 = \left( \sum_{i=1}^nx_i^2\right)^{\frac{1}{2}} = (x^tx)^{\frac{1}{2}}$$
이제 고유값 $\lambda$에 대한 기하학적인 의미를 알아보자. 이때 설명의 편의를 위해 $v$를 단위 벡터($\|v \|_2 = 1$)라 하겠다. $Av$의 기하학적인 의미를 먼저 살펴보자. $Av$를 풀어쓰면 다음과 같다.
$$\begin{align} Av &= \begin{pmatrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \cdots & a_{nn} \end{pmatrix}v \\ &= \begin{pmatrix} \tilde{a}_1^t \\ \tilde{a}_2^t \\ \vdots \\ \tilde{a}_n^t \end{pmatrix}v = \begin{pmatrix} \tilde{a}_1^tv \\ \tilde{a}_2^tv \\ \vdots \\ \tilde{a}_n^tv \end{pmatrix} \end{align}$$
여기서 $\tilde{a}_i^t = (a_{i1}, \ldots, a_{in})$는 $A$의 $i$번째 행벡터이다. 이때 $\tilde{a}_i^tv$는 $A$의 $i$번째 행벡터의 벡터의 $v$위의 정사영(projection)인 것을 알 수 있다. 즉, $Av$의 $i$번째 원소는 $A$의 $i$번째 행벡터의 $v$위의 정사영이라는 것이다(아래 그림 참고).

이제 $\|Av\|_2$를 계산해 보자.
$$\begin{align} \|Av\|_2 &= (v^tA^tAv)^{\frac{1}{2}} \\ &= (\lambda^2v^tv)^{\frac{1}{2}} \\ &= (\lambda^2)^{\frac{1}{2}} \\ &= |\lambda| = \lambda \end{align}$$
여기서 3번째 등식은 $v$가 단위 벡터이기 때문이고 마지막 등식은 $\lambda$가 음이 아닌 정수이기 때문이다. 이를 통해 알 수 있는 것은 고유값은 $A$의 행벡터에 대한 고유 벡터 위로의 정사영들의 Euclidean Norm이라는 것이다. 즉, 정사영들의 제곱합의 제곱근이라는 것이다.
c. 고유값 계산 방법
(1)을 다시 쓰면 다음과 같다.
$$(A-\lambda I)v = 0 \tag{2}$$
여기서 $I$는 $n\times n$ 단위행렬이다. 만약 $(A-\lambda I)$가 역행렬이 있다면 $v$는 0 벡터가 된다. 하지만 고유 벡터는 0벡터가 아니므로 $(A-\lambda I)$의 역행렬이 존재하지 않아야 한다. 즉, 고유값 $\lambda$를 계산하려면 다음을 풀어야 한다.
$$\text{det}(A-\lambda I) = 0$$
d. 예제
다음 행렬의 고유값과 고유 벡터를 계산해 보자.
$$A = \begin{pmatrix}1 & 2 \\ 2 & 1\end{pmatrix}$$
풀이
$$\begin{align} \text{det}(A - \lambda I) &= \left | \begin{pmatrix} 1-\lambda & 2 \\ 2 & 1-\lambda \end{pmatrix} \right | \\ &= (1-\lambda)^2-4 \\ &= \lambda^2-2\lambda - 3 \\ &= (\lambda-3)(\lambda +1) = 0 \end{align}$$
따라서 $A$의 고유값은 -1과 3인 것을 알 수 있다. 먼저 고유값 3에 대응하는 고유 벡터를 찾아보자. $v = (x, y)$라 할 때 $v, \lambda = 3$을 (2)에 집어넣고 풀면 다음과 같다.
$$\begin{pmatrix} -2 & 2 \\ 2 & -2 \end{pmatrix} \begin{pmatrix} x \\ y \end{pmatrix} = \begin{pmatrix} 0 \\ 0\end{pmatrix} \\ \Rightarrow x=y $$
따라서 고유값 3에 대응하는 고유 벡터는
$$k\begin{pmatrix} 1 \\ 1 \end{pmatrix}, k\in \mathbb{R}$$
인 것을 알 수 있다. 편의상 단위 벡터로 설정한다면 고유 벡터는 다음과 같다.
$$\left ( 1/\sqrt{2}, 1/\sqrt{2} \right ) = (0.7071, 0.7071)$$
비슷한 방법으로 계산하면 -1에 대응하는 고유 벡터는 다음과 같다는 것을 알 수 있다.
$$\left ( -1/\sqrt{2}, 1/\sqrt{2} \right ) = (-0.7071, 0.7071) $$
e. 파이썬 예제
Numpy 모듈의 linalg.eig를 이용하면 주어진 행렬의 고유값과 고유벡터를 알 수 있다.
import numpy as np
A = np.array([[1, 2], [2, 1]])
eigen_values, eigen_vectors = np.linalg.eig(A) ## 각각 고유값 배열과 고유벡터 배열을 리턴한다.
for i in range(len(eigen_values)):
print(f'고유값 {eigen_values[i]:.1f}, 고유 벡터 {eigen_vectors[:, i]:}')

2. 고유값 분해
a. 정의
$n\times n$ 행렬 $A$가 $n$개의 선형 독립인 고유 벡터가 존재할 때 $A$를 대각화 가능하다고 한다. 고유값 분해의 정의는 다음과 같다.
고유값 분해
대각화 가능한 행렬 $A$는 다음과 같이 분해될 수 있다.
$$A = Q\Lambda Q^{-1}$$
이때 $\Lambda$는 대각 행렬이고 $\Lambda_{ii} = \lambda_i$로 $A$의 $i$번째(임의 순서) 고유값이며 이에 대응하는 고유 벡터(단위 벡터)를 $q_i$라 할 때 이를 $i$번째 칼럼으로 하는 행렬이 $Q$이다.
b. 고유값 분해의 필요성
고유값 분해를 이용하면 행렬 곱 연산을 쉽게 할 수 있다. 예를 들어 $A^n$을 계산한다고 해보자. 이때 고유값 분해를 이용하면
$$A^n = (Q\Lambda Q^{-1})^n = Q\Lambda^nQ^{-1}$$
임을 알 수 있다. 이때 $\Lambda$는 대각 행렬이므로 $\Lambda^n$은 각 대각 원소를 $n$승하면 얻을 수 있다. 따라서 위 식을 이용하면 원래는 $n-1$번의 행렬 곱 연산을 해야 하지만 단 2번의 행렬 곱 연산만 수행하면 $A^n$을 계산할 수 있는 것이다.
또한 주어진 행렬 $A$가 대칭 행렬인 경우 대각화가 가능하고 그에 따라 고유값 분해가 가능하며 이 경우 역행렬 계산이 굉장히 쉬워진다. $A$가 대칭 행렬이면 임의의 두 고유 벡터는 수직(Orthogonal)이 된다. 이 경우 고유값 분해를 통해 역행렬을 계산해 보자.
$$\begin{align} A^{-1} &= (Q\Lambda Q^{-1})^{-1}\\ &= Q\Lambda^{-1}Q^{-1}\\ &= Q\Lambda^{-1}Q^t \end{align}$$
여기서 4번째 등식은 $Q$가 Orthonormal이기 때문에 가능하다. 여기서 $\Lambda$는 대각 행렬이기 때문에 $\Lambda^{-1}$은 대각 원소의 역수를 취하면 얻을 수 있고 $Q^{-1}$를 $Q$의 전이 행렬 $Q^t$로 변환되며 결국 남은 건 행렬 곱셈 밖에 없어지므로 $A$의 Determinant 계산 필요 없이 쉽게 역행렬을 계산할 수 있는 것이다.
c. 예제
다음 행렬의 고유값 분해식을 구해보자.
$$A = \begin{pmatrix}1 & 2 \\ 2 & 1\end{pmatrix}$$
우리는 앞에서 $A$의 고유값은 3, -1이고 이에 대응하는 고유 벡터는 각각 $\left ( 1/\sqrt{2}, 1/\sqrt{2} \right ), \left ( -1/\sqrt{2}, 1/\sqrt{2} \right )$ 임을 알았다. 따라서
$$Q = \begin{pmatrix} 1/\sqrt{2} & -1/\sqrt{2} \\ 1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix} \\ Q^{-1} = \begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} \\ -1/\sqrt{2}& 1/\sqrt{2} \end{pmatrix}$$
이고 $A$의 고유값 분해식은
$$A = \begin{pmatrix}1 & 2 \\ 2 & 1\end{pmatrix} = \begin{pmatrix} 1/\sqrt{2} & -1/\sqrt{2} \\ 1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix} \begin{pmatrix} 3 & 0 \\ 0 & 1 \end{pmatrix} \begin{pmatrix} 1/\sqrt{2} & 1/\sqrt{2} \\ -1/\sqrt{2} & 1/\sqrt{2} \end{pmatrix}$$
이다.
d. 파이썬 예제
Numpy 모듈의 linalg.eig를 이용하면 주어진 행렬의 고유값 분해식을 구할 수 있다. linalg.eig의 첫 번째 리턴값은 주어진 행렬의 고유값 배열이 되므로 diag를 이용하여 대각 행렬 $\Lambda$를 만들 수 있다. 두 번째 리턴값은 고유값 분해식에서 $Q$가 된다. 이를 이용하여 고유값 분해식을 만든 다음 원래의 주어진 행렬과 일치하는지 살펴보자.
import numpy as np
A = np.array([[1, 2], [2, 1]])
eigen_values, eigen_vectors = np.linalg.eig(A) ## 고유값과 Q 행렬
Lambda = np.diag(eigen_values) ## 람다 대각 행렬
print(eigen_vectors @ Lambda @ np.linalg.inv(eigen_vectors)) ## 원 행렬과 같은지 확인

정확하게 주어진 행렬과 일치하는 것을 알 수 있다.
'통계 > 기타' 카테고리의 다른 글
| 특이값 분해(Singular Value Decomposition : SVD)에 대해서 알아보자(feat. Numpy) (0) | 2023.03.07 |
|---|---|
| ANOVA(Analysis of Variance, 분산분석)에 대해서 알아보자. (7) | 2022.12.06 |
| 통계학이란 무엇인가? (0) | 2022.11.07 |
| 가중치를 활용한 통계량을 알아보자. 가중 평균(Weighted Mean), 가중 상관계수(Weighted Correlation), 가중 분위수 (Weighted Quantile) (2) | 2022.09.25 |
| Profile Likelihood 란 무엇인가?! (408) | 2022.04.30 |





댓글