이번 포스팅에서는 Reduced Rank Regression에 대한 개념과 파이썬 구현 방법을 알아보고자 한다. 여기서는 기본적인 선형 대수 지식과 특이값 분해(Singular Vector Decomposition : SVD)에 대한 지식이 있다고 가정한다.
1. Reduced Rank Regression(RRR)이란?
특이값 분해(Singular Vector Decomposition : SVD)에 대해 잘 모르시는 분들은 아래에 포스팅해두었으니 참고하면 도움이 된다.
특이값 분해(Singular Value Decomposition : SVD)에 대해서 알아보자(feat. Numpy)
1. Reduced Rank Regression(RRR)이란?
1) 정의
Reduced Rank Regression(RRR)은 다변량 다중 선형 회귀 모형에서 여러 반응 변수를 설명하기 위한 변수의 개수를 rank를 이용하여 줄이는 회귀 추정법이다.
2) 파헤치기
RRR에 대해서 하나씩 파헤처보자.
a. 다변량 다중 선형 모형
데이터($y$가 여러 개인 경우) $(x_i, y_i), x_i\in \mathbb{R}^p, y_i\in \mathbb{R}^q, i=1, \ldots, n$가 있다고 하자. 이제 다음과 같은 모형을 생각해 보자.
$$y_{ij} = x_i^tb_j + \epsilon_{ij}, \;\; i=1, \ldots, n, \;\; j=1, \ldots, q \tag{1}$$
이때 $b_j = (b_{j1}, \ldots, b_{jp})^t$으로 $j$번째 반응 변수에 대한 회귀 계수 벡터이며 $e_{ij}$는 오차항을 나타낸다. (1)을 다변량 다중 선형 회귀 모형이라 한다. 다변량은 $y$가 여러 개, 다중은 $x$가 여러 개인 것을 뜻한다.
(1)을 벡터로 표현하면 다음과 같다.
$$y_j = Xb_j+e_j , j=1, \ldots, q\tag{2-1}$$
(1)을 행렬로 표현하면 다음과 같다.
$$Y_{n\times q} = X_{n\times p}B_{p\times q}+E_{n\times q} \tag{2-2}$$
다변량 다중 선형 회귀는 일반적으로 Frobenius Norm으로 계산된 잔차 제곱을 최소화하는 회귀 계수 행렬 $B$를 찾는다.
$$\|Y-XB\|_F^2 = \text{tr}\left ((Y-XB)^t(Y-XB) \right ) \tag{3} $$
(3)을 만족하는 것은 $\hat{B} = (X^tX)^{-}X^tY$이다. 이때 $A^-$은 $A$의 일반화 역행렬(Generalized Inverse)이다. $\hat{b}_j$를 $\hat{B}$의 $j$ 번째 칼럼이라고 하면 다음을 알 수 있다.
$$\hat{b}_j = (X^tX)^{-}X^ty_j$$
여기서 $y_j$는 $Y$의 $j$ 번째 칼럼이다. 이를 통해 단변량(y가 하나인 거) 다중 선형 회귀 모형
$$y_{ij} = x_i^tb_j+\epsilon_{ij}$$
를 $q$번 수행하여 회귀 계수 벡터 $\hat{b}_j$을 얻는 것과 동일하다는 것을 알 수 있다. 따라서 행렬로 표현한 다변량 선형 회귀 모형은 여러 번 추정해야 할 것을 한 번에 추정한다는 것 외에는 별다른 이점이 없다. 따라서 $B$에 특별한 제약을 주는 것을 고려하게 되었다. 그게 바로 $B$의 rank를 줄이는 것이다.
b. rank을 이용하여 변수의 차원을 줄인다.
RRR은 회귀 계수 행렬 $B$의 rank를 작게 하여 변수의 개수(차원)를 줄인다. rank와 관련된 정리 하나를 소개한다.
정리 1
$\text{rank}(B) = k$의 필요충분조건은
$$B = U_{p\times k}V_{k \times q}, \;\;\text{rank}(U) = \text{rank}(V) = k$$
위 정리를 통해 회귀 계수 행렬 $B$의 rank를 작게 하는 것이 설명 변수의 차원을 줄여준다는 것을 설명할 수 있다. $\text{rank}(B)=k$라 할 때 $B$의 $j$번째 칼럼 벡터를 $b_j$라 하자. 그렇다면 정리 1을 통해 다음을 알 수 있다.
$$ b_j = Uv_j = v_{1j}u_1+v_{2j}u_2+\cdots +v_{kj}u_k $$
여기서 $u_j, v_j$는 각각 $U, V$의 $j$번째 칼럼 벡터이며 $v_j = (v_{1j}, \ldots, v_{kj})^t$이다.
$Y$의 $j$번째 칼럼 벡터의 추정치를 $\hat{y}_j$라할 때 다음을 알 수 있다.
$$\begin{align}\hat{y}_j &= b_{1j}x_1+b_{2j}x_2+\cdots + b_{pj}x_p \\ &= Xb_j \\ &= X\left ( v_{1j}u_1+v_{2j}u_2+\cdots +v_{kj}u_k \right ) \\ &= v_{1j}u_1'+v_{2j}u_2'+\cdots+v_{kj}u_k' \end{align}\tag{4}$$
여기서 $u_j' = Xu_j$이고 $x_j$는 $X$의 $j$ 번째 칼럼 벡터이다. $u_j'$은 $X$의 칼럼 벡터로 생성하는 칼럼 스페이스의 원소(쉽게 말하면 기존 $X$의 칼럼 벡터의 선형 결합이며 이는 기존 설명 변수 벡터의 선형 결합을 의미한다)이며 이를 통해 $u_j'$으로 생성한 벡터 공간은 $X$의 칼럼 스페이스에 부분 집합이 되는 것을 알 수 있다(아래 그림 참고).

(4)의 의미는 ($k$를 $p$보다 작게 설정한 경우) $q$개의 반응 변수 벡터 $y_j$를 $p$개보다 더 적은 $k$개의 기존 설명 변수 벡터의 선형 결합 $u_j'$로 설명이 가능하다는 것이며 이는 기존 $p$차원에서 $k$로 차원을 줄이는 효과가 있다는 것이다(아래 그림 참고).

이제 rank를 작게 하는 것이 설명 변수의 차원을 줄이는 것임을 알았다.
RRR은 회귀 계수 행렬의 rank를 작게 설정하여 회귀 계수 행렬 $B$를 추정하고 이는 다변량 반응 변수를 설명하기 위한 변수의 개수(차원)를 줄이는 효과가 있다.
3) 추정 방법
RRR은 기존 최소 제곱 프레임에 rank 제약이 있는 문제를 풀어서 회귀 계수 행렬 $B$를 추정한다.
$$\text{minimize} \;\; \|Y-XB \|_F^2\;\; \text{with constraint rank}(B) \leq k \tag{5}$$
Reduced Rank Regression(RRR) 모형 추정 방법에는 특이값 분해(Singular Value Decomposition)를 이용하는 방법과 최대 우도 추정(Maximum Likelihood Estimation)을 이용한 방법이 있다. 각각에 대해서 살펴보자.
a. 특이값 분해(SVD)를 이용한 RRR 추정 방법
먼저 일반적인 최소 제곱 추정량 $\hat{B}$에 대하여 $\hat{Y} = X\hat{B}$이라 하자. 그렇다면 (3)은 다음과 같이 제곱합 분해가 된다.
$$\| Y-XB\|_F^2 = \|Y-\hat{Y} \|_F^2+\| \hat{Y} - XB\|_F^2$$
이는 $(Y-\hat{Y})^t(\hat{Y}-XB)=0$이기 때문이다. 오른쪽에서 첫 번째 항은 $B$와는 무관하므로 이를 통해 (5)는 다음과 같이 쓸 수 있다.
$$\text{minimize} \;\; \|\hat{Y}-XB \|_F^2\;\; \text{with constraint rank}(B) \leq k \tag{6}$$
이때 $\hat{Y}$에 SVD를 적용하여 얻은 표현식이 다음과 같다고 하자.
$$\hat{Y} = U\Sigma V^t$$
위 식에서 $k$가 주어졌을 때 처음 $k$ 개의 특이값을 이용하여 만든 대각행렬 $\Sigma_k$ 그리고 $U, V$에서 처음 $k$개 특이값에 대응하는 칼럼 벡터로 만들어진 행렬을 각각 $U_k, V_k$라 하자. 그리고 $\hat{Y}_k$를 다음과 같이 정의한다.
$$\hat{Y}_k = U_k\Sigma_kV_k^t$$
이때 $\hat{Y}_k$를 $\hat{Y}$의 $k$ 축소 SVD 표현식이라고 정의하자. 이 경우 $\text{rank}(\hat{Y}_k)=k$이다.
이때 RRR을 SVD를 이용하여 추정하는 이론의 기반이 되는 정리 하나를 소개하겠다. 바로 Eckart-Young-Mirsky 정리이다.
Eckart-Young-Mirsky 정리
$A$의 $k$ 축소 SVD 표현식을 $A_k=U_k\Sigma_k V^t_k$라 하자. 그렇다면 $\text{rank}(A_k) = k$이고 다음이 성립된다.
$$\| A- A_k\|_F^2 \leq \| A-A_k\|_F^2 \;\; \forall \;\; B \;\;\text{with rank}(B)\leq k$$
이때
$$\| A-A_k\|_F^2 = \sum_{i=1}^ks_i^2$$
여기서 $s_i, i=1, \ldots, k$는 $k$ 축소 SVD 표현식에서 나타나는$k$개의 특이값이다.
Eckart-Young-Mirsky 정리를 이용하면 $\text{rank}(M) \leq k$인 $M$에 대하여 $\|\hat{Y}-M \|_F^2$을 최소화하는 것은 $M=\hat{Y}_k$임을 알 수 있다. (6)에서 우리가 찾고자 하는 회귀 계수 행렬 $B$는 $\text{rank}(B)\leq k$이므로
$$\text{rank}(XB) \leq \text{rank} \leq k$$
가 된다. 이를 통해 다음을 알 수 있다.
$$\| \hat{Y}-XB\|_F^2 \geq \| \hat{Y}-\hat{Y}_k\|_F^2 \;\; \forall B \;\;\text{with rank}(B)\leq k \tag{7}$$
(7)이 의미하는 바는 만약 $XB = \hat{Y}_k$인 $B$를 찾을 수 있다면 이는 곧 (6)의 (Frobenius Norm 값이 글로벌 최소가 되므로) 해가 된다는 것이다.
$\hat{B}_k = \hat{B}V_kV_k^t$로 세팅한다면 $X\hat{B}_k=\hat{Y}_k$가 되며 $\hat{B}_k$가 RRR 추정량이 되는 것이다.
이제 RRR에서 SVD를 이용한 추정 단계를 알아보자.
1 단계) $k$를 설정하고 $n \times q$ 행렬 $Y$와 $n\times p$ 행렬 $X$ 대해서 각 칼럼 별로 표본 평균을 빼준다(Centering). 이때 $Y$에 대해서는 표본 표준편차로 나누어 표준화를 수행할 수도 있다.
2 단계) (3)을 최소화하는 기존 최소 제곱 추정량 $\hat{B}$을 계산한다.
3 단계) 반응 변수의 적합 행렬 $\hat{Y} = X\hat{B}$를 계산한 뒤 이에 대하여 SVD 표현식을 구한다.
$$\hat{Y} = U\Sigma V^t$$
4 단계) 위 SVD 표현식을 이용하여 $k$ 축소 SVD 표현식을 유도하고 이를 통해 $V_k$를 얻는다.
5 단계) RRR 추정량 $\hat{B}_k = \hat{B}V_kV_k^t$를 얻는다.
b. 최대 우도 추정(Maximum Likelihood Estimation)
최대 우도 추정을 이용한 추정 방법은 Petre Stoica, Mats Vibergdml 1996년 논문 "Maximum Likelihood Parameter and Rank Estimation in Reduced-Rank Multivariate Linear Regression"에서 제안한 방법을 소개하며 대략적인 방법에 대해서 소개한다.
먼저 다변량 선형 회귀 모형을 다음과 같이 가정한다.
$$y_i = Bx_i+e_i, i=1, \ldots, n \tag{8}$$
여기서 $y_i \in \mathbb{R}^q, x_i \in \mathbb{R}^p, e_i \in \mathbb{R}^m, B\in \mathbb{R}^{q\times p}$
(8)과 (2-1)의 차이점은 (8)은 행렬 $Y$의 행 벡터를 기준으로 표현한 것이고 (2-1)은 칼럼 벡터를 이용하여 표현한 것이다. (8)은 논문에서 제시한 모형을 그대로 따랐다.
최대 우도 추정을 위해 아래와 같은 3가지 가정을 한다.
가정 1)
오차 벡터 $e_i$는 평균이 0이고 알려지지 않은 공분한 행렬 $Q$를 갖는 다변량 정규 분포이다.
$$Q = E[e_ie_i^t], |Q|\neq 0$$
그리고 서로 다른 오차 벡터 간에는 다음을 만족한다.
$$E[e_ie_j^t] = 0 \;\; \text{for} \;\; i\neq j$$
가정 2)
$x_i$는 결정적 신호(Deterministic Signal)이며 다음을 만족한다.
$$\begin{align} &\lim_{n\rightarrow \infty} \frac{1}{n}\sum_{i=1}^nx_ix_i^t=R_{xx}, \;\; |R_{xx}|\neq 0 \\ &\lim_{n\rightarrow \infty} \frac{1}{n}\sum_{i=1}^nx_ie_i^t = 0 \;\; \text{w. p. 1} & \end{align}$$
가정 3)
$B$의 rank는 미지이며 실제 rank는 작다는 것이 알려져 있다. 즉,
$$\text{rank}(B) = k < \min (p, q) $$
$\text{rank}(B) = k$ 이면 $B$를 $\text{rank}(U) = \text{rank}(V)=n$이고 사이즈가 각각 $q\times k, p \times k$인 두 행렬 $U, V$의 곱으로 표현할 수 있다.
$$ B = UV^t$$
가정 1)을 이용하면 우리가 최대화하고자하는 로그 우도 함수는 다음과 같다는 것을 알 수 있다.
$$L = -\frac{n}{2}\left ( \log |Q| +\text{tr}(Q^{-1}C(U, V)) \right) + \text{const.}\tag{9}$$
이때
$$C(U, V) = \frac{1}{n}\sum_{i=1}^n\left ( y_i - UV^tx_i \right ) \left ( y_i-UV^tx_i \right )^t\tag{10}$$
RRR에서 $B$를 최대 우도 추정법으로 추정하는 단계는 다음과 같다.
1 단계) $Q$ 제거
$Q$를 모르기 때문에 $U, V$ 뿐만 아니라 $Q$까지 추정해야한다. 이때 Profiling 기법을 쓴다. 먼저 $U, V$를 고정시키고 (9)를 최대화하는 $Q$를 찾아야 한다. 만약 모든 $U, V$에 대하여 $C(U, V)$가 양정치 행렬이라면 (9)를 최소화하는$Q$는 다음과 같다는 사실이 알려져 있다.
$$Q=C(U, V)\tag{11}$$
2 단계) $U$ 제거
(11)을 이용하면 로그 우도 함수는 다음과 같이 정리된다.
$$L = -\frac{n}{2}\log |C(U, V)| + \text{const.}\tag{12}$$
$V$를 고정시키고 $U$를 (12)를 최대화하는 $U$는 미분을 통하여 다음과 같음을 알 수 있다.
$$U = \hat{R}_{yx}V(V^t\hat{R}_{xx}V)^{-1} \tag{13}$$
여기서
$$\hat{R}_{yx} = \frac{1}{n}\sum_{i=1}^ny_ix_i^t$$
이고 다른 것들도 비슷하게 정의된다.
3 단계) $V, U, B, Q$ 추정
(13)을 이용하여 로그 우도 함수를 정리하면 다음과 같다.
$$\begin{align} L &= -\frac{n}{2} \log|\hat{R}_{yy} - \hat{R}_{yx}V(V^t\hat{R}_{xx}V)^{-1}V^t\hat{R}_{yx}^t | +\text{const.} \\ &= -\frac{n}{2} \log |\hat{R}_{yy}^{-1} | |\hat{R}_{yy} - \hat{R}_{yx}V(V^t\hat{R}_{xx}V)^{-1}V^t\hat{R}_{yx}^t | + \frac{n}{2}\log |\hat{R}_{yy} | + \text{const.} \\ &= -\frac{n}{2} \log |I - \hat{R}_{yy}^{-1/2} \hat{R}_{yx}V(V^t\hat{R}_{xx}V)^{-1}V^t\hat{R}_{yx}^t \hat{R}_{yy}^{-1/2} | + \text{const.} ' \\ &= -\frac{n}{2} \log |I - \Omega| + \text{const.} ' \end{align}\tag{14}$$
여기서
$$\Omega (V) = \hat{R}_{yy}^{-1/2} \hat{R}_{yx}V(V^t\hat{R}_{xx}V)^{-1}V^t\hat{R}_{yx}^t \hat{R}_{yy}^{-1/2} $$
이다.
$V$의 rank가 $k$이므로 $\text{rank}(\Omega (V)) \leq k$이다. $\Omega (V)$의 고유값을 내림차순 했을 때 처음 $k$개의 고유값들을 $\mu_j(V), j=1, \ldots, k$라 하자. 그렇다면 (14)를 다음과 같이 정리할 수 있다.
$$\begin{align} L &= -\frac{n}{2} \log \left ( \prod_{j=1}^k(1-\mu_j(V)) \right ) + \text{const.}' \\ &= -\frac{n}{2} \sum_{j=1}^k\log (1-\mu_j(V)) +\text{const.}' \end{align} \tag{15} $$
(15)를 최대화하기 위해 $\mu_j(V)$를 최대화해야 하며 $\mu_j(V)$를 최대화할 수 있는 $V$를 찾으면 된다. 이를 위해 필요한 정리가 푸엥카레의 분리 정리(Poincaré Separation Theorem)이다. 이 정리는 대칭 행렬 고유값의 한계(Bound)에 대한 정리이다.
푸엥카레의 분리 정리(Poincaré Separation Theorem)
$A$를 $n\times n$ 대칭 행렬이라 하고 $B$를 ${n\times r}$ Semi-Orthogonal 행렬이라 하자. 즉, $B^tB=I_r$. 이때 $\lambda_i$와 $\mu_i$를 각각 $A$와 $B^tAB$의 내림차순으로 정렬된 고유값이라 하자. 그러면 다음이 성립한다.
$$\lambda_i \geq \mu_i \geq \lambda_{n-r+i}, i=1, \ldots, r$$
$X, W$를 다음과 같이 정의하자.
$$\begin{align} X &= (V^tR_{xx}V)^{-1/2}V^tR_{xx}^{1/2} \\ W &= \hat{R}_{xx}^{-1/2}\hat{R}_{yx}^t \hat{R}_{yy}^{-1} \hat{R}_{yx}\hat{R}_{xx}^{-1/2}\end{align}$$
$W$의 고유값을 내림차순으로 정렬한 것을 $\lambda_1 \geq \lambda_2 \geq \cdots \geq \lambda_p$라 하고 이에 대응하는 고유 벡터를 $v_j, j=1, \ldots, p$라 하자. 그러면
$X^tX = I_{k\times k}$이고
$$\begin{align} X^tWX &= (V^tR_{xx}V)^{-1/2}V^t R_{yx}^tR_{yy}^{-1}R_{yx}V(V^tR_{xx}V)^{-1/2} \\ &= AA^t \end{align}$$
여기서 $A = (V^tR_{xx}V)^{-1/2}V^t R_{yx}^tR_{yy}^{-1/2}$이다. $A^tA = \Omega$이므로 $XWX(=AA^t)$의 고유값은 $\Omega$의 고유값인 $\mu_j(V)$가 된다. 따라서 푸엥카레의 분리 정리에 의하여 다음이 성립한다.
$$\mu_j(V) \leq \lambda_j, j=1, \ldots, k\tag{16}$$
이때 등호는 $X$의 칼럼 벡터가 $\lambda_j$의 고유 벡터 $v_j$로 이루어진 경우에 성립한다. 이를 $S$라 하자. 즉,
$$S = (v_1\; v_2\; \cdots v_k)$$
또한 $\hat{V} = \hat{R}_{xx}^{-1/2}S $도 (16)의 등호를 만족한다. 따라서 $\hat{V}$이 (15)를 최대화하는 추정량, 즉 $V$의 최대 우도 추정량이 된다. (13)을 이용하면 $U$의 최대 우도 추정량 $\hat{U}$을 계산할 수 있고
$B$의 최대 우도 추정량 $\hat{B} = \hat{U}\hat{V}^t$도 구할 수 있다. (10)을 이용하면 $Q$의 최대 우도 추정량도 계산할 수 있다.
이 논문의 저자는 RRR의 SVD 기반의 추정량과 최대 우도 추정량을 비교했는데 오차의 공분산 행렬이 공간 상관성(Spatially Correlation)이 존재하면 최대 우도 추정량이 SVD 기반 추정량 보다 MSE 관점에서 더 좋다고 한다.
논문의 저자는 $B$의 최대 우도 추정량을 계산하는 방법을 다음과 같이 단순화하였다.
$B$의 최대 우도 추정량 계산
1 단계) 아래의 행렬을 QR 분해한다.
$$ \frac{1}{\sqrt{N}}\begin{pmatrix} x_1^t & y_1^t \\ \vdots & \vdots \\ x_n^t & y_n^t \end{pmatrix} = \tilde{Q} \begin{pmatrix} R_{11} & R_{21} \\ 0 & R_{22} \end{pmatrix}$$
여기서 $R_{11}$은 $p\times p$, $R_{22}$는 $q\times q$ 상삼각(Upper Triangular) 행렬이다.
2 단계) $R_{21}, R_{22}$를 이용하여 QR 분해를 한번 더 실시한다.
$$\begin{pmatrix} R_{21} \\ R_{22} \end{pmatrix} = \bar{Q} \begin{pmatrix} R_{1} \\ 0 \end{pmatrix} $$
3 단계) $R_{21}R_1^{-1}$의 SVD를 수행한다.
$$R_{21}R_1^{-1} = V\Sigma U^t \tag{17}$$
이때 $S = (v_1\;v_2 \; \cdots \; v_k)$를 $k$개의 왼쪽 특이 벡터(Left Singular Vector)로 이루어진 행렬이라 하자.
4 단계) $B$의 최대 우도 추정량을 계산한다.
$$\hat{B} = R_{21}^tSS^tR_{11}^{-t}$$
본 논문에는 추정량의 점근적 성질과 SVD 기반 추정량의 실험 결과가 포함되어 있으므로 관심 있는 분들은 해당 논문을 참고하면 된다.
3) 최적 rank $k$ 설정
지금까지는 회귀 계수 행렬의 rank를 $k$로 주어졌다고 가정했다. 하지만 실제 회귀 계수 행렬의 rank는 모른다. 따라서 $k$의 후보군을 정한 다음 특정 기준에 최적화된 $k$를 골라야 할 것이다. 여기서는 최적 $k$를 고르는 방법에 대해서 소개한다.
a. Scree Plot(Elbow Plot)
기본적으로 생각해 볼 수 있는 것은 반응 변수 행렬 $Y$와 이에 대응하는 예측 행렬 $\hat{Y}$의 차이를 어느 정도 작게 하는 $k$를 선택할 수 있을 것이다. 이는 $k$값에 대하여 $\|Y-\hat{Y}\|_F^2$ 값을 그려봄으로써 시각적으로 확인할 수 있다.
b. 통계적 검정
통계적으로 최적 $k$를 선정하는 방법은 다음과 같다.
1 단계) 유의 수준 $\alpha$를 선정한다.
2 단계) 각 $k$에 대하여 검정 통계량 $T$을 계산한다. 특이값 분해를 이용한 RRR 모형을 추정했다면 아래의 검정 통계량을 사용한다.
$$T_{\text{SVD}} = \sum_{j=k+1}^q s_j^2 $$
여기서 $s_j$는 $\hat{Y}$을 특이값 분해한 경우에 나타나는 $j$ 번째 특이값이다.
최대 우도 추정을 이용했다면 아래의 검정 통계량을 사용한다.
$$T_{\text{ML}} = -n\sum_{j=k+1}^{\min (p, q)}\log (1-\lambda_j)$$
여기서 $\lambda_j$는 (17)에서 $j$ 번째 특이값의 제곱이다.
$T_{\text{SVD}}, T_{\text{ML}}$ 모두 귀무가설 $H_0 : \text{rank}(B) = k$을 검정하는 통계량이며 귀무가설이 참일 때 검정 통계량의 분포는 모두 자유도가 $(q-k)(p-k)$인 카이제곱 분포를 따른다.
3 단계) 유의 확률 $p=P(\chi^2 \geq T_{\text{SVD}})$(또는 $P(\chi^2 \geq T_{\text{ML}})$)을 계산한다. 그러고 나서 $p>=\alpha$를 만족하는 가장 작은 값을 최적 $k$로 정한다.
2. 파이썬 구현
이제 앞에서 배운 것들을 토대로 RRR 모형 추정 과정을 구현해 보자. 아래 코드에서 ReducedRankRegression은 특이값 분해 또는 최대 우도 추정 방법을 이용하여 회귀 모형을 적합(fit)한다. 이때 rank 검정을 위한 검정 통계량과 pval도 같이 계산(_get_pval)하도록 했다. 마지막으로 예측을 수행하는 함수(predict)도 구현했다. 주목할 것은 최대 우도 추정 방법에서 예측을 $XB$ 형태로 하기 위해 _fit_mle에서 계산한 회귀 계수 행렬의 열과 행을 바꾸어주었다(line 61).
import numpy as np
import pandas as pd
from scipy.stats import chi2
class ReducedRankRegression:
def __init__(self, rank):
self.rank = rank ## rank
self.B = None ## 회귀 계수 행렬 추정치
self.test_stat = None ## 검정 통계량
self.pval = None ## pvalue
def _get_pval(self, p, q, rank, test_stat): ## pval 계산 함수
dof = (p-rank)*(q-rank)
chi_rv = chi2(dof)
return 1-chi_rv.cdf(test_stat)
def fit(self, Y, X, method='svd'): ## 모형 적합
assert method in ['svd', 'mle'] ## svd : 특이값 분해, mle : 최대 우도 추정
assert self.rank <= np.min([Y.shape[1], X.shape[1]])
rank = self.rank
if method == 'svd':
self._fit_svd(Y, X, rank)
else:
self._fit_mle(Y, X, rank)
return self
def _fit_svd(self, Y, X, rank): ## 특이값 분해 이용
p, q = X.shape[1], Y.shape[1]
B_ols = np.linalg.inv(X.T @ X) @ X.T @ Y
Y_hat = X @ B_ols
_, Sigma, V_t = np.linalg.svd(Y_hat)
reduced_V_t = V_t[:rank, :]
B_rrr = B_ols @ reduced_V_t.T @ reduced_V_t
self.B = B_rrr
test_stat = np.sum(np.square(Sigma[rank:]))
self.test_stat = test_stat
self.pval = self._get_pval(p, q, rank, test_stat)
def _fit_mle(self, Y, X, rank): ## 최대 우도 추정 이용
n = X.shape[0]
p, q = X.shape[1], Y.shape[1]
XY = (1/np.sqrt(n))*np.c_[X, Y]
_, R = np.linalg.qr(XY)
R_11 = R[:p, :p]
# R_22 = R[-q:, -q:]
R_22 = R[p:, p:]
R_21 = R[:p, p:]
new_R = np.concatenate([R_21, R_22])
_, R_bar = np.linalg.qr(new_R)
R_bar_1 = R_bar[:q, :q]
U, Sigma, _ = np.linalg.svd(R_21 @ np.linalg.inv(R_bar_1))
S_hat = U[:, :rank]
B_ml = (R_21.T@S_hat@S_hat.T@np.linalg.inv(R_11.T)).T
self.B = B_ml
test_stat = -n*np.sum(np.log(1-np.square(Sigma[rank:np.min([p, q])])))
self.test_stat = test_stat
self.pval = self._get_pval(p, q, rank, test_stat)
def predict(self, X): ## 예측값
return X@self.B
3. 예제
앞에서 구현한 클래스를 사용해 보자. 다변량 데이터에 대한 마땅한 예제가 없어서 R에서 모의실험을 위한 데이터를 생성해주는 함수가 여기에 있길래 데이터를 만들어주었다. 모의 실험 데이터는 아래에 첨부해 두었으며 각각 $X, Y$ 데이터이고 실제 회귀 계수의 rank는 7이다.
데이터를 불러온 뒤 rank를 4로 설정하고 RRR 모형을 특이값 분해, 최대 우도 추정 방법을 이용하여 추정해 보았다. 그리고 모형의 성능을 보기 위하여 실제값과 추정값의 차이를 Frobenius Norm으로 계산하였다.
X = pd.read_csv('x.csv', header=None)
Y = pd.read_csv('y.csv', header=None)
X = X.values
Y = Y.values
rank = 4
svd_rrr = ReducedRankRegression(rank).fit(Y, X) ## 특이값 분해
mle_rrr = ReducedRankRegression(rank).fit(Y, X, method='mle') ## 최대 우도 추정
## 실제값과 추정값의 차이
print('SVD_RRR Residual :', np.mean(np.square(Y-svd_rrr.predict(X))))
print('MLE_RRR Residual :', np.mean(np.square(Y-mle_rrr.predict(X))))

이번엔 최적 $k$를 선택해 보자. 먼저 Elbow Plot(Scree Plot)을 통해서 최적 $k$를 시각적으로 선택할 수 있는지 확인해 보자. $k$의 후보군을 정하고 각 $k$에 대하여 잔차의 평균 Frobenius Norm 값을 추정 방법 별로 그려보았다.
## Determination of rank
import matplotlib.pyplot as plt
k_list = [5,6,7,8,9,10]
svd_res_list = []
mle_res_list = []
for k in k_list:
svd_rrr = ReducedRankRegression(k).fit(Y, X)
mle_rrr = ReducedRankRegression(k).fit(Y, X, method='mle')
svd_res = np.mean(np.square(Y-svd_rrr.predict(X)))
mle_res = np.mean(np.square(Y-mle_rrr.predict(X)))
svd_res_list.append(svd_res)
mle_res_list.append(mle_res)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.plot(k_list, svd_res_list, color='r', marker='o', label='SVD')
ax.plot(k_list, mle_res_list, color='k', marker='o', label='MLE')
ax.legend()
plt.show()
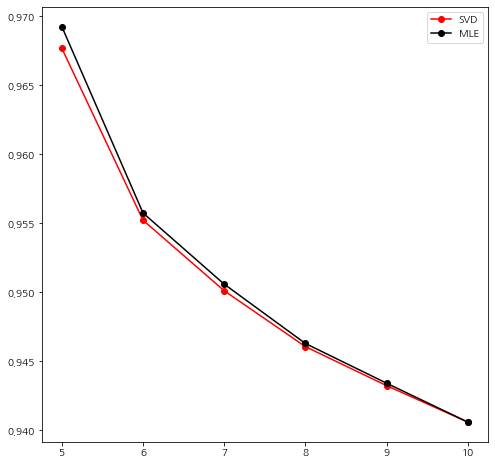
그림을 살펴보니 두 방법 모두 6에서 가장 크게 감소했으며 7부터는 감소폭이 줄어들었다. 사실 이것만 가지고는 잘 모르겠다 ㅎㅎ;;
이번엔 통계적 검정 방법을 사용해 보자. 유의 수준을 0.05로 설정하고 유의 확률이 0.05 보다 큰 것들 중에서 가장 작은 $k$를 선택한다.
alpha = 0.05 ## 유의 수준
k_list = [3,4,5,6,7,8,9] ## k 후보
svd_pval = []
mle_pval = []
for k in k_list:
svd_rrr = ReducedRankRegression(k).fit(Y, X)
mle_rrr = ReducedRankRegression(k).fit(Y, X, method='mle')
svd_pval.append((k, svd_rrr.pval))
mle_pval.append((k, mle_rrr.pval))
print('SVD Optimal k :', min([x[0] for x in svd_pval if x[1] >= alpha]))
print('MLE Optimal k :', min([x[0] for x in mle_pval if x[1] >= alpha]))

두 결과 모두 최적 rank는 6을 선택했다. 실제 rank(7)와 1 차이가 났다.
4. 장단점
- 장점 -
a. 회귀 계수 행렬이 좋은 통계적인 성질을 갖고 있다.
최대 우도 추정법을 이용한 RRR 추정량의 경우 일치성을 만족한다고 한다.
b. 최적 Rank를 통계적인 검정 방법을 이용하여 정할 수 있다.
c. 차원 축소 효과가 있다.
RRR 추정량의 행렬 크기는 기존 최소 제곱 추정량과 같지만 더 작은 rank를 갖고 있어 설명 변수의 차원 축소 효과가 있다.
d. 구현이 쉽다.
- 단점 -
a. 이상치에 민감하다.
RRR은 이상치에 민감하며 고차원 데이터의 경우 굉장히 왜곡된 Low Rank 구조를 만들어낼 수 있다.
b. 설명 변수의 다중 공선성에도 민감하다.
- 참고 자료 -
Davis, P. T., Tso, M. K-S : Procedure for Reduced-Rank Regression
Petre Stoica, Mats Viberg : Maximum Likelihood Parameter and Rank Estimation in Reduced-Rank Multivariate Linear Regression
She, Y, Chen, K : Robust Reduced-Rank Regression





댓글