이번 포스팅에서는 Spline Regression에 대한 개념과 Smoothing Spline 그리고 Penalized B-Spline에 대한 내용을 소개한다. 이때 Smoothing Spline을 설명하기 위해 Truncated Power Basis, Cubic Spline을 먼저 소개한 후 Smoothing Spline에 대한 내용을 다룬다. Smoothing Spline의 특수한 경우로 Natural Spline 또한 소개한다. B-Spline에 대한 개념을 소개한 뒤 Penalized B-Spline을 알아본다. 파이썬으로 구현하는 방법도 소개한다.
- 목차 -
1. Spline Regression이란 무엇인가?
1) 정의
Spline Regression은 데이터 상에 매듭점을 정하고 매듭점으로 나누어진 영역을 잘 설명하는 비모수 회귀 모형 추정법을 말한다.
2) 파헤치기
앞에서 정의한 내용을 자세히 살펴보자. Spline Regressions을 알아보려면 먼저 Spline이 무엇인지 알아야 한다. 또한 설명의 편의를 위하여 우리가 추정하고자 하는 함수는 1차원 실수 집합(변수가 하나인 데이터)에서 정의된 함수라 하겠다.
a. Spline 이란?
Spline은 매듭점 사이를 충분히 매끄럽게 연결해주는 함수이다. Spline의 수학적 정의는 다음과 같다.
Spline의 정의
함수 $f : \mathcal{R} \rightarrow \mathcal{R}$이 아래 2개의 조건을 만족한다면 $f$를 매듭점 $\tau_1<\cdots <\tau_n$에 대한 $k(\geq 1)$차 Spline이라고 한다.
(1) $f$는 개별 구간 $(-\infty, \tau_1], [\tau_1, \tau_2], \ldots, [\tau_n, \infty)$위에서 $k$차 다항 함수이다. 0차 다항 함수는 Constant 함수이다.
(2) $k\geq 1$인 경우 $j=0, \ldots, k-1$ 번째 미분 $f^{(j)}$이 각 매듭점 $\tau_1, \tau_2, \ldots, \tau_n$ 에서 연속이다.
Spline은 매듭점 위에서 매끄럽지 않을 수 있지만 (2)번 조건과 같이 미분 함수의 연속성이 만족된다면 매끄럽게 되는 것이다. 미분의 연속성과 매끄러운 정도는 직관적으로도 연관성이 있다. $x$좌표를 이동시켜가면서 $f$의 순간 변화율이 급격하게 변하지 않아야 매끄러운 것이며 이는 미분의 연속성을 의미한다.
예를 들어 매듭점 $x=0$인 경우의 연결된 함수가 아래 왼쪽 그림과 같다고 해보자. 한눈에 봐도 0인 점에서 뾰족, 다시 말해 매끄럽지 않다. $x=-1$에서 0에 가까워질수록 순간 변화율이 일정하다가 0인 지점에서 급격하게 변한다. 이는 1차 미분 함수가 연속이 아니라는 점을 보더라도 알 수 있다(오른쪽 그림).
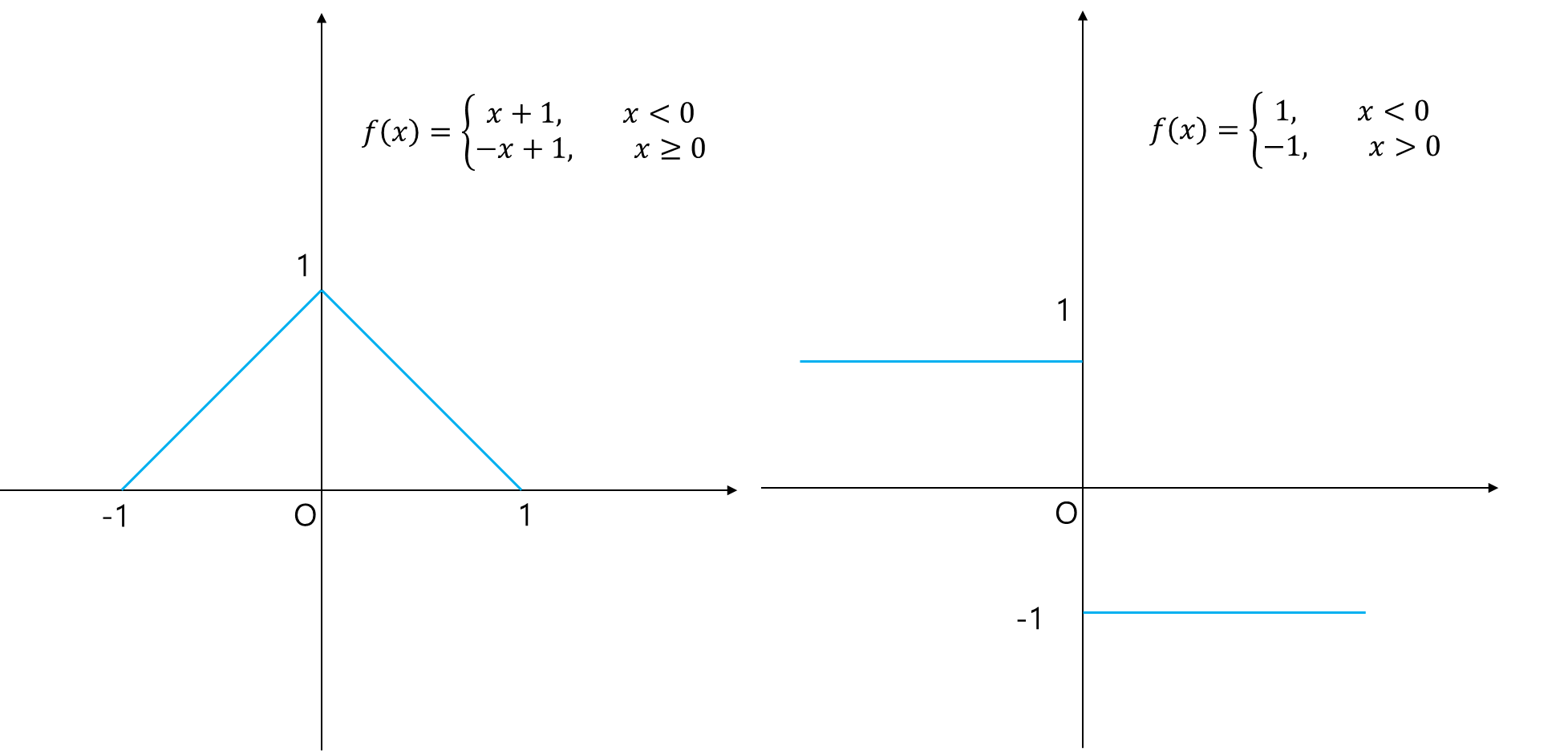
아래 그림은 매듭점 0을 연결하는 매끄러운 함수를 나타낸 것(왼쪽 그림)이며 1차 미분이 $x=0$에서 연속인 것을 알 수 있다(오른쪽 그림).

매듭점을 사용하는 이유?
기존 선형 회귀 모형에서는 계수를 데이터 전체를 이용하여 추정한다. 하지만 예측을 할 때에는 특정 입력값 주변 부분에서 더 큰 영향을 미치는 것이 합리적이다. 따라서 매듭점을 이용하여 데이터 전체가 아닌 매듭점 사이 구간의 모형을 사용하여 예측을 좀 더 정확하게 하자는 취지이다.
이제 Spline의 뜻을 알았으니 Spline Regression에 대해서 자세히 설명할 수 있다.
b. Spline Regression은 데이터 상에서 매듭점 정한다.
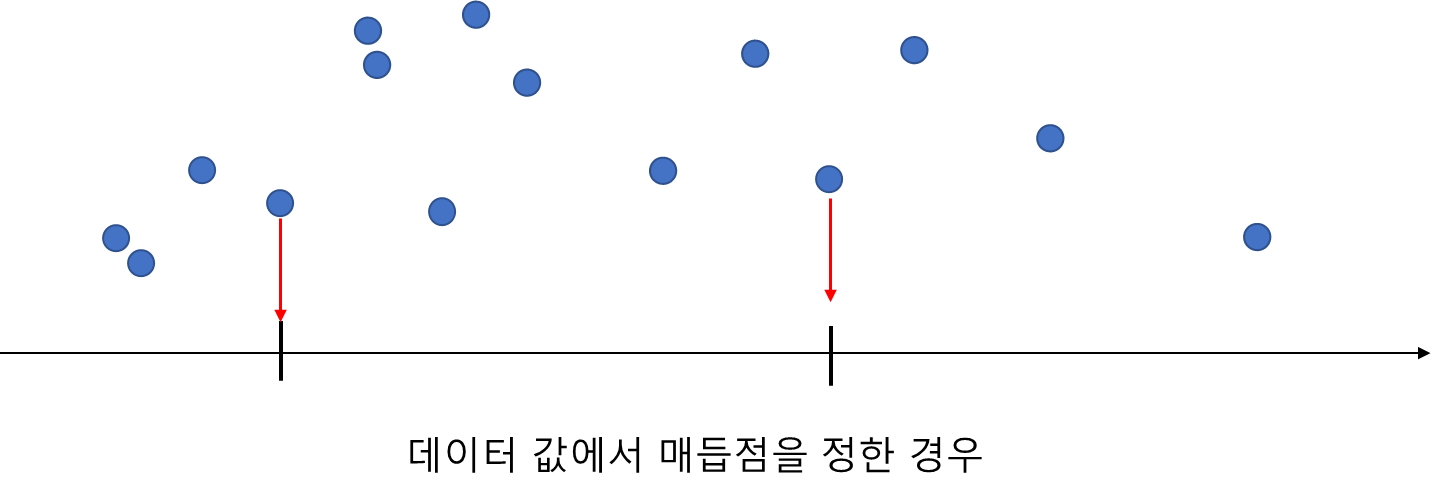
Spline Regression은 데이터 상에서 매듭점의 개수와 위치를 정하게 된다. 여기서 데이터 상이라는 말은 주어진 데이터 최소값과 최대값 사이를 의미한다. 매듭점의 개수와 위치를 정하는 방법에는 개수가 정해지면 각 매듭점 사이의 간격이 일정하도록 위치를 설정하거나 데이터 포인트 중에서 변수 선택법으로 선택하는 방법 등 여러 가지가 있다. 아래 그림들은 매듭점 2개를 정하는 방법을 나타낸 것이다.

c. Spline Regression은 기저 함수의 선형 결합으로 회귀 모형을 잘 근사하는 비모수 추정법이다.
Spline은 매듭점 사이의 구간을 다항식으로 적합하게 된다. 이때 효율적으로 적합하기 위하여 기저 함수 집합을 고려하게 된다. 기저 함수가 없으면 각 구간별로 다항 모형을 적합해야하나 기저 함수를 도입하면 한 방에 적합할 수 있다.
실수 집합 $\mathbb{R}$에서 정의된 유한개의 기저 함수(Basis Function) 집합 $\{B_1(x), \ldots, B_N(x)\}$가 있다고 해보자. Spline Regression은 회귀 함수 $f(x) = E(y|x)$를 이러한 기저 함수들의 선형 결합으로 근사한다.
$$f(x) \approx \sum_{i=j}^Nb_jB_j(x)$$
여기서 $b_j, j=1, \ldots, N$은 실수이다.
기저 함수라는 것은 특정 함수 공간에 있는 임의의 함수를 만들어내는 함수 집합의 원소들이라고 할 수 있다. 예를 들어 실수상에서 정의된 함수들의 특정 집합(함수 공간)을 $\mathcal{F}$라 하고 $\{ B_n(x) \}_{n=1}^{\infty}$을 기저 함수 집합이라 한다면 함수 공간 내 임의의 함수 $f \in \mathcal{F}$는 기저 함수들의 선형결합으로 표현된다.
$$f(x) = \sum_{n=1}^{\infty}b_nB_n(x)\tag{1}$$
만약 우리가 계산하고자 하는 회귀 함수가 $\mathcal{F}$에 들어간다면 이 회귀 함수를 정확하게 추정하려면 (1)과 같이 계산해야 할 것이다. 하지만 실제로 기저함수 무한개로 이루어진 선형결합을 계산하기는 어려우므로 유한개의 기저 함수의 선형 결합으로 근사한 것이다. 즉, Spline Regression은 회귀 함수를 모수적( parametric)으로 추정하려면 무한개의 $b_n$을 추정해야 하지만 현실적으로 이것이 어려워 유한개로 근사한 것이다. 그런 의미에서 Spline Regression은 비모수 회귀 추정법이다(실제로는 무한개의 모수로 이루어져있으므로).
하지만 유한한 모수 $b_1, \ldots, b_N$도 기저 함수 관점에서 보면 선형 회귀와 유사한 문제로 볼 수 있으므로 Spline Regression은 진정한 의미에서 비모수가 아니라고 주장하는 학자들도 있다.
d. Spline Regression은 연속성, 미분 연속성 제약식이 있는 최소 제곱법을 풀어서 계수 $b_1, \ldots, b_N$을 추정한다.
주어진 데이터 $(x_i, y_i), x_i, y_i \in \mathbb{R}, i=1, \ldots, n$에 대하여 기저 함수 집합 $B_1(x), \ldots, B_N(x)$가 정해졌다면 최소 제곱법을 이용하여 이에 대응하는 계수 $b_1, \ldots, b_N$을 추정하게 된다.
이때 계수 벡터 $b = (b_1, \ldots, b_N)^t$의 최소 제곱 추정량 $\hat{b}$는 다음과 같다.
$$\hat{b} = (B^tB)^{-1}B^ty$$
여기서 $y=(y_1, \ldots, y_n)^t$이고 $n\times N$행렬 $B$는 다음과 같다.
$$B = \begin{pmatrix} B_1(x_1) & B_2(x_1) & \cdots & B_N(x_1) \\ B_1(x_2) & B_2(x_2) & \cdots & B_N(x_2) \\ \vdots & \vdots & \ddots & \vdots \\ B_1(x_n) & B_2(x_n) & \cdots & B_N(x_n) \\ \end{pmatrix} \tag{2}$$
이때 $k$차 Spline을 적용한다면 Spline 정의에서 (2)번 조건을 만족하는 제약식이 추가될 수 있다(아닐 수도 있다). 이는 어떤 Basis를 사용하느냐에 따라서 달라지므로 해당 내용을 소개할 때 구체적인 모형 적합 방법을 알아보기로 한다. 이때 (벌점항이 없는) 최소 제곱법을 통해 얻어진 모형 $\hat{f} = \hat{b}_1B_1(x) + \cdots + \hat{b}_NB_N(x) $를 Regression Spline이라 한다.
Piecewise Regression과 Spline Regression의 차이!!
Piecewise Regression도 매듭점으로 만들어진 개별 구간에 대해서 회귀 모형을 적합한다. 따라서 매듭점을 사용한다는 관점에서 Spline Regression과 별 차이가 없어 보일 수 있다. 하지만 Piecewise Regression은 매듭점에서 연속이 아니어도 되지만 Spline Regression은 매듭점에서 급격한 변화는 있을지라도 연속성은 보장된다(아래에서 살펴보겠지만 연속인 기저 함수들의 선형 결합이기 때문이다).
이제 Spline Regression에 대한 개념을 알았으니 종류에는 어떤 것들이 있는지 살펴보고자 한다.
2. Smoothing Spline
Smoothing Spline을 알아보기 전에 몇 가지 개념을 짚고 넘어가자.
1) Truncated Power Basis
a. 정의
특정 매듭점 $\tau$에서의 $k$차 Truncated Power Function(TPF)은 다음과 같이 정의된다.
$$(x-\tau)_{+}^k = \begin{cases} 0 \;\; \text{if}\;\; x < \tau \\ (x-\tau)^k \;\; \text{o.w.} \end{cases}$$
Piecewise Polynomial Regression(PPR)과 Truncated Power Function을 포함하는 기저 함수를 이용한 Spline Regression(SR)의 차이점을 살펴보자. 예를 들어 매듭점이 $\tau_1, \tau_2(\tau_1<\tau_2)$ 두 개 있고 그에 따라 영역이 3개가 될 텐데 각 영역에서 직선(1차 Spline)을 적합시킨다고 해보자. 이때 연속성을 만족하는 PPR과 SR의 차이를 살펴보겠다.
먼저 PPR을 살펴보자. PPR은 다음과 같이 개별 구간에 대하여 직선을 적합한다.
$$f(x) = (b_{10} + b_{11}x)B_1(x)+(b_{20} + b_{21}x)B_2(x)+(b_{30}+b_{31}x)B_3(x)\tag{2.1}$$
여기서 $B_1(x) = I(x<\tau_1), B_2(x)=I(\tau_1\leq x<\tau_2), B_3(x) = I(x\geq\tau_2)$ 이다.
이때 매듭점 $\tau_1, \tau_2$에서 연속이어야 하므로 다음을 만족해야 한다.
$$f(\tau_1^{-}) = b_{10}+b_{11}\tau_1=b_{20}+b_{21}\tau_1 = f(\tau_1^{+}) \\ f(\tau_2^{-}) = b_{20}+b_{21}\tau_2=b_{30}+b_{31}\tau_2 = f(\tau_2^{+})\tag{2.2}$$
총모수가 6개이지만 제약식이 2개가 생기므로 자유도는 4가 된다.
이제 다음과 같은 1차 TPF를 포함하는 기저 함수들을 생각해 보자. 이를 1차 Truncated Power Basis(TPB)라 한다.
$$B_1(x) = 1, B_2(x) = x, B_3(x) = (x-\tau_1)_{+}, B_4(x) = (x-\tau_2)_{+}$$
그리고 위 기저함수들로 SR은 다음과 같은 모형을 적합한다.
$$f(x) = b_0B_1(x) + b_1B_2(x)+b_2B_3(x)+b_3B_4(x)\tag{2.3}$$
각 구간에서 (2.3)의 모형을 정리하면 다음과 같다.
$$f(x) = \begin{cases} b_0+b_1x & \text{if} \;\; x < \tau_1 \\ b_0-b_2\tau_1 + (b_1+b_2)x & \text{if} \;\; \tau_1 \leq x < \tau_2 \\ b_0-b_2\tau_1-b_3\tau_2+(b_1+b_2+b_3)x & \text{o.w.} \end{cases} \tag{2.4}$$
(2.4)를 통해 알 수 있는 것은 4개의 기저 함수를 이용해도 PPR과 같이 구간별로 적합한 것과 동일한 효과를 얻을 수 있다는 것이다. 왜냐하면 이미 연속이기 때문에 연속을 만족하도록 제약을 가할 필요가 없어 자유도가 동일하게 4개이기 때문이다. (2.4)가 (2.1) 보다 좋은 이유는 제약식 없이 적합하면 되므로 문제가 쉬워지기 때문이다.
일반적으로 매듭점의 개수가 $K$이고 $p$차 다항식인 경우 PPR는 $K+1$영역에 각각 $p+1$개의 모수를 추정해야 하고 Spline 정의의 (2) 번 조건을 만족하기 위한 제약식이 매듭점 하나에 대하여 $p$개 만큼 생긴다. 매듭점의 개수는 $K$개 이므로 제약식이 총 $pK$개가 된다. 따라서 자유도 다음과 같다.
$$(K+1)(p+1)-pK = p+1+K$$
이번엔 $p$차 TPB를 살펴보자. $p$차 TPB는 다음과 같이 $p$차 다항식과 매듭점에 대한 $p$차 TPF를 포함하는 형태로 정의한다.
$$\begin{align}B_j(x) &= x^{j-1}, \;\; j=1, \ldots, p+1 \\ B_{p+1+l} &= (x-\tau_l)_{+}^p, \;\; l=1, \ldots, K \end{align}$$
$p$차 TPB의 선형 결합은 이미 $p$차 Spline이다. 다시 말해 Spline의 조건을 만족하므로 제약식이 없다. 따라서 계수의 총 개수 $p+1+K$이 자유도가 된다.
즉, 일반적인 $p$차 Spline의 경우도 $p$차 PPR보다 $p$차 TPB로 모형을 적합할 경우 자유도의 손실이 없으며 제약식이 없기 때문에 더 풀기 편한 문제가 된다.
b. 모형 적합
주어진 데이터 $(x_i, y_i), x_i, y_i \in \mathbb{R}, i=1, \ldots, n$에 대하여 $p$차 TPB를 사용한 경우 아래와 같은 잔차 제곱을 최소화하는 계수 $b = (b_0, \ldots, b_p, b_{p+1}, \ldots, b_{p+K})^t$를 추정한다.
$$ \min_{b \in \mathbb{R}^{p+1+K}} \sum_{i=1}^n(y_i - b_0 B_1(x_i) - \cdots - b_{p+K}B_{p+1+K}(x_i))^2$$
이때 계수 벡터 $b = (b_0, \ldots, b_{p+K})^t$의 최소 제곱 추정량 $\hat{b}$는 다음과 같다.
$$\hat{b} = (B^tB)^{-1}B^ty$$
여기서 $y=(y_1, \ldots, y_n)^t$이고 $n\times (p+1+K)$행렬 $B$는 다음과 같다.
$$B = \begin{pmatrix} B_1(x_1) & B_2(x_1) & \cdots & B_{p+1+K}(x_1) \\ B_1(x_2) & B_2(x_2) & \cdots & B_{p+1+K}(x_2) \\ \vdots & \vdots & \ddots & \vdots \\ B_1(x_n) & B_2(x_n) & \cdots & B_{p+1+K}(x_n) \\ \end{pmatrix}$$
c. 고려 사항
모형 적합을 위해서 고려사항이 몇 가지 있다. 바로 다항 차수 $p$, 매듭점의 개수 그리고 매듭점의 위치이다. 이때 생각해 볼 수 있는 방법은 다음과 같다.
먼저 $p$차 TPB를 $\mathcal{B}(p, m)$로 표현한다. 이때 $m$은 매듭점의 개수이다. 매듭점 개수가 정해지면 매듭점의 위치는 백분위수로 정한다. 예를 들어 $\mathcal{B}(3, 4)$인 경우 다항 차수는 3, 매듭점의 개수는 4개이며 매듭점의 위치는 20, 40, 60, 80 백분위수로 정하는 것이다.
이제 $p$와 $m$의 후보군을 정하고 각 후보에 대하여 모형을 적합한다. 그러고 나서 가장 적합력(또는 검증 데이터를 이용한 예측력)이 좋은 $p^*$와 $m^*$를 최종 다항 차수와 매듭점 개수로 정하게 된다.
d. 파이썬 예제
이번엔 TPB를 이용한 Spline Regression을 수행하는 클래스를 구현해보고자 한다. 아래 TPBSpline이 바로 그것이다. 이 클래스는 매듭점과 다항 차수를 초기값으로 갖는다. 클래스의 구조를 살펴보면 TPB를 생성하는 create_tpb, TPB를 기반으로 X 행렬을 만들어주는 make_X_matrix, 그리고 모형을 적합하는 fit 마지막으로 새로운 데이터에 대해서 예측을 수행하는 predict 메서드로 구성되어 있다.
import numpy as np
import pandas as pd
from functools import partial
from sklearn.linear_model import LinearRegression
class TPBSpline:
def __init__(self, knots, p):
self.knots = knots ## 매듭점 배열
self.p = p ## 다항 차수
self.basis = None ## Truncated Power Function Basis 배열
self.X = None ## X matrix
self.coef_ = None ## 회귀 계수
def create_tpb(self, p, knots): ## Truncated Power Function Basis 생성
def poly(x, p):
return x**p
def hinge(x, p, knot):
return (x - knot)**p if x > knot else 0
temp = [partial(poly, p=i) for i in range(p+1)] + [partial(hinge, p=p, knot=knot) for knot in knots]
self.basis = np.array(temp)
def make_X_matrix(self, array): ## X matrix 생성
p = self.p
knots = self.knots
self.create_tpb(p, knots)
basis = self.basis
self.X = np.array([[b(x=x) for b in basis] for x in array])
def fit(self, array, y): ## 모형 적합
self.make_X_matrix(array)
X = self.X
y = np.array(y)
reg = LinearRegression(fit_intercept=False).fit(X, y)
self.coef_ = reg.coef_
return self
def predict(self, array):
basis = self.basis
temp = [self.coef_.dot([b(x=x) for b in basis]) for x in array]
return np.array(temp)
이제 실제 데이터를 이용하여 TBP Spline Regression 모형을 적합해보자. 데이터는 3000명의 남성 작업자의 임금 데이터로 해당 데이터는 여기에서 다운받을 수 있다.
이제 데이터를 불러온 다음 y를 wage 칼럼, x를 age로 하겠다. 이때 매듭점은 25, 40, 60으로 정하였으며 다항 차수는 3차로 정했다(Cubic Spline). 그렇다면 $p=3, K=3$이므로 절편항을 포함하여 총 7($=p
+1+K$)개의 파라미터를 추정해야 한다.
df = pd.read_csv('dataset-37830.csv')
x = df['age'].values
y = df['wage'].values
tpb_spline = TPBSpline(knots=[25, 40, 60], p=3).fit(x, y)
모형 적합 후 계수를 살펴보면 다음과 같다.
tpb_spline.coef_

이제 결과를 시각화해 보자. age를 x축, wage를 y축으로 하는 산점도와 적합된 모형 곡선을 그려보았다.
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(10,6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(x, y, color='k', alpha=0.3)
age_grid = np.arange(df['age'].min(), df['age'].max())
pred = tpb_spline.predict(age_grid)
ax.plot(age_grid, pred, color='r')
for xc in [25, 40, 60]:
ax.axvline(xc, linestyle='--', color='b')
ax.set_xlabel('Age')
ax.set_ylabel('Wage')
plt.show()

꽤나 부드러운 곡선이 적합된 것을 알 수 있다.
이번엔 최적 매듭점의 개수와 위치를 선택해 보자. 여기에서는 다항 차수 $p=3$으로 고정시켰다. 아래 코드는 매듭점의 개수를 3~10으로 변화시키고 위치는 그에 대응하는 백분위수로 설정한 다음 매듭점의 개수와 학습 평균 잔차 제곱을 시각화한다. 여기서는 학습 평균 잔차 제곱을 가장 작게 하는 매듭점의 개수를 선택하려고 한다(검증을 위해서라면 데이터를 학습데이터와 검증데이터로 나누어서 해야 할 것이다).
knot_nums = np.arange(3, 10)
p = 3
mse_list = []
for knot_num in knot_nums:
knots = [np.percentile(x, (i+1)/(knot_num+1)*100) for i in range(knot_num)]
tpb_spline = TPBSpline(p=p, knots=knots).fit(x, y)
y_pred = tpb_spline.predict(x)
mse = np.sqrt(np.mean(np.square(y-y_pred)))
mse_list.append(mse)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.plot(knot_nums, mse_list)
plt.show()

매듭점의 개수가 8개일 때 학습 평균 잔차 제곱이 가장 낮은 것을 알 수 있다. 따라서 매듭점의 개수를 8개로 설정해 놓고 TPB Spline Regression 모형을 적합하여 그 적합력을 시각화해 보자.
knot_num = 8
knots = [np.percentile(x, (i+1)/(knot_num+1)*100) for i in range(knot_num)]
tpb_spline = TPBSpline(p=p, knots=knots).fit(x, y)
fig = plt.figure(figsize=(10,6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(x, y, color='k', alpha=0.3)
age_grid = np.arange(df['age'].min(), df['age'].max())
pred = tpb_spline.predict(age_grid)
ax.plot(age_grid, pred, color='r')
for xc in knots:
ax.axvline(xc, linestyle='--', color='b')
ax.set_xlabel('Age')
ax.set_ylabel('Wage')
plt.show()

2) Cubic Spline
Cubic Spline은 기저함수 집합으로 $3$차 TPB의 선형 결합을 말한다. $K$개 매듭점에 대하여 3차 TPB은 다음과 같다(특별한 언급이 없다면 매듭점의 개수는 $K$로 하겠다).
$$\begin{align}B_j(x) &= x^{j-1}, \;\; j=1, \ldots, 4 \\ B_{4+l} &= (x-\tau_l)_{+}^3, \;\; l=1, \ldots, K \end{align}$$
그렇다면 우리가 추정하고 싶은 함수 $f$는 다음과 같이 3차 TPB의 선형 결합으로 표현된다.
$$f(x) = \sum_{j=0}^3b_jx^j+\sum_{j=1}^K\theta_j(x-\tau_j)^3_+\tag{2.5}$$
Cubic Spline이 특별히 중요한 이유는 아래에서 다룰 Smoothing Spline이 최소화하고자 하는 목적함수의 전역 해가 되기 때문이다(정확히는 Natural Cubic Spline 이다). 또한 The Elements of Statistical Learning(5.2) 에서 저자는 매듭점 불연속성을 사람의 눈으로 확인할 수 없는 최소의 다항 차수가 3이라는 것이 일반적인 주장이다. 이 말이 뭔 말이냐 하면 1차, 2차 TPB까지는 매듭점에서 급격하기 꺾이거나 하는 등의 변화를 눈으로 볼 수 있지만 3차 TPB부터는 그런 게 잘 안 보인다는 것이다. 또한 회귀 모형 적합 시 차수가 3보다 큰 TPB를 쓰는 경우는 많이 없다고 하며 차수가 커지면 심각한 부동 소수점 오류가 발생할 수 있다고 한다.
3) Smoothing Spline
a. 정의
Smoothing Spline은 매듭점에서 매끄러운 것뿐만 아니라 매듭점 사이에서도 매끄럽게 하기 위해 급격하게 변하는 것에 대한 Penalty를 고려한 Spline을 말한다. 그렇다면 이러한 Smoothing Spline은 어떻게 얻을 수 있는지 살펴보자.
매끄러운 정도는 다음과 같이 미분을 적분하여 측정할 수 있다.
$$\int_{-\infty}^{\infty} \left\{ f^{(m)}(x) \right \}^2 dx \tag{2.6}$$
고정된 $m=1, 2, \ldots$에 대하여 (2.6)의 값이 클수록 $f$의 변동이 심하고 작을수록 매끄럽다는 것이다. 따라서 기존 잔차 제곱항에 (2.6)를 벌점항으로 추가하여 모형을 적합하면 Smoothing Spline을 얻을 수 있는 것이다. 이때 Schoenberg는 다음과 같은 이론을 증명하였다.
정리 1. Schoenberg(1964)
주어진 데이터 $(x_i, y_i), x_i, y_i \in \mathbb{R}, i=1, \ldots, n$가 있고 $x_1 < \cdots < x_n$이라고 하자. 이때 정수 $m(\leq n)$과 $\lambda(\geq 0)$에 대하여
$$\sum_{i=1}^n(y_i-f(x_i))^2+\lambda \int_{-\infty}^{\infty} \left\{ f^{(m)}(x) \right \}^2 dx \tag{2.7} $$
최소화하는 함수 $\hat{f} \in \{ f : f^{(m)}\in L^2 \}$가 유일하게 존재하며 $\hat{f}$은 다음을 만족한다.
(1) $\hat{f}$는 $(-\infty, \infty)$에서 연속인 $(2m-2)$ 미분을 갖는다.
(2) $\hat{f}$는 구간 $(x_i, x_{i+1}), i=1, \ldots, n$에서 $(2m-1)$차 다항 함수이다.
(3) $\hat{f}$는 구간 $(-\infty, x_1)$과 $(x_n, \infty)$에서 $(m-1)$차 다항 함수이다.
이때 $\hat{f}$를 $k(=2m-1)$차 Natural Spline이라고 한다.
위 식이 의미하는 바는 잔차 제곱을 통해 설명력을 좋게 하면서 변동성이 낮은 즉, 매끄러운 함수를 유일하게 찾을 수 있다는 것이 된다. 이때 $m=2$인 경우에 식 (2.7)은 다음과 같다.
$$\sum_{i=1}^n(y_i-f(x_i))^2+\lambda \int_{-\infty}^{\infty} \left\{ f''(x) \right \}^2 dx, \lambda \geq 0 \tag{2.8}$$
이때 (2.8)을 최소화하는 $f$를 Natural Cubic Spline이라 한다.
(2.8)의 첫 번째 항은 함수 $f$가 얼마나 데이터와 가까운지를 나타내는 측정하고 두 번째 항에서 적분값이 작으면 매끄럽게 변하는 것이고 크면 전체적으로 또는 특정 지점에서 급격하게 변하는 것이 있다는 것이다. 이때 우리는 이 값이 작은 것을 선호한다. 왜냐하면 급격하게 변하는 지점에서의 예측 또는 추정값이 매우 불안정하기 때문이다. 따라서 이러한 불안정성을 없애고자 매끄러운 함수를 선호한다. 따라서 두 번째 항은 급격하게 변하는 다시 말해 곡률(Curvature)이 커지는 것을 방지하기 위한 벌점항으로 볼 수 있다. 이때 $\lambda$는 평활 모수(smoothing parameter)라 하는데 두 가지 특수한 경우를 살펴보자.
1) $\lambda=0$인 경우
(반복 측정이 없는 경우) (2.8)을 만족하는 $f$는 $(x_i, y_i), i=1, \ldots, n$을 지나는 모든 함수가 될 것이다.
2) $\lambda=\infty$인 경우
(2.8)을 만족하는 함수 $f$는 기껏해야 1차 함수일 것이다(단순 선형 회귀와 같아진다). 2차 이상의 함수가 되는 순간 (2.8)이 $\infty$가 되어 최소화할 수 없기 때문이다.
따라서 이러한 극단적인 경우를 제외하고 $\lambda \in (0, \infty)$에서 평활 모수를 선택하게 된다. $\lambda$가 정해졌다면 이제 우리의 관심사는 (2.8)을 최소화하는 $\hat{f}$를 찾는 것이다.
이론적으로 (2.8)을 최소화하는 것은 유니크한 $x_i$들을 매듭점으로 하는 Natural Cubic Spline이라는 것이 알려져 있다. 따라서 Smoothing Spline 문제에서는 유니크한 $x_i$들을 매듭점으로 설정하면 되므로 매듭점 개수와 위치를 선택할 필요가 없어진다.
즉, Smoothing Spline의 핵심은 매듭점의 개수와 위치를 찾는 것이 어려우니까 데이터로부터 발생하는 매듭점을 모두 사용하고 대신 곡률에 대한 벌점을 고려하여 매끄러운 함수 $f$를 추정하자는 것이다.
b. 모형 적합
이번엔 Cubic Spline(3차 TPB)을 생각해 보자. Cubic Spline은 정리 1에서 조건 (1), (2)를 만족한다. 하지만 Boundary Condtion인 (3)을 만족하지 않는다. Cubic Spline이 Natural Cubic Spline이 되려면 일단 (3)을 만족해야 한다. (3)을 만족하기 위한 (2.5)의 제한 조건은 다음과 같다.
$$b_2 = 0, b_3 = 0 \\ \sum_{j=1}^K\theta_j = 0, \sum_{j=1}^K\theta_j\tau_j=0 \tag{2.9}$$
(2.9)는 결국 매듭점 바깥에서 2차, 3차 미분이 0이 되기 위한 조건이다. 4개의 제약식이 생기므로 (3) 조건을 만족하는 3차 TPB의 자유도는 $K(=4+K-4)$가 된다.
즉, (2.8)을 최소화하는 문제를 풀어야 하는데 조건 (2.9)까지 체크해야 한다. 이러한 불편함을 없애기 위해 (2.9)를 만족하는 3차 TPB가 생성하는 집합과 같으면서 제약식이 없는 크기가 $K$인 아래의 기저 함수 집합을 고려하게 된다.
$$N_1(x) = 1, N_2(x) = x, N_{j+2}(x) = d_j(x) - d_{K-1}(x) \;\; j=1, \ldots, K-2 \tag{2.10}$$
여기서
$$d_j(x) = \frac{(x-\tau_j)^3_{+} - (x-\tau_K)^3_{+}}{\tau_K-\tau_j}$$
이다.
이제 새로운 기저 함수 집합을 이용하여 $f$를 표현하면 다음과 같다.
$$f(x) = \sum_{j=1}^K\beta_j N_j(x) \tag{2.11}$$
그리고 (2.8)을 행렬식으로 표현하면 다음과 같다.
$$(y-N\beta)^t(y-N\beta) + \lambda \beta^t\Omega \beta \tag{2.11}$$
여기서 $y=(y_1, \ldots, y_n)^t$, $\beta=(\beta_1, \ldots, \beta_K)^t$, $n\times K$ 행렬 $N$은 $N_{ij} = N_j(x_i)$, $K\times K$ 행렬 $\Omega$는 $\Omega_{ij} = \int N''_i(t) N''_j(t) dt$이다.
(2.11)은 $\beta$에 대해서 Convex 문제이며 미분이 가능하므로 아래와 같이 쉽게 (2.11)의 해 $\hat{\beta}$를 계산할 수 있다.
$$\hat{\beta} = (N^tN + \lambda \Omega)^{-1}N^ty$$
그리고 우리가 추정하는 함수 $\hat{f}$는 다음과 같다.
$$f(x) = \sum_{j=1}^K\hat{\beta}_j N_j(x) \tag{2.12}$$
(2.9)의 증명
$f(x) = \sum_{j=0}^3b_jx^j+\sum_{j=1}^K\theta_j(x-\tau_j)^3_+$라 할 때 우리가 보여야할 것은 Boundary에서($x\leq \tau_1, x\geq \tau_K$)에서 $f$가 1차 다항 함수가 되기 위한 조건이 (2.9)라는 것이다.
먼저 모든 $x\leq \tau_1$에 대하여 다음을 알 수 있다.
$$(x-\tau_j)^3_+ = 0, j=1, \ldots, K$$
따라서 $f(x) = b_0+b_1x+b_2x^2+b_3x^3, x\leq \tau_1$이 된다. $x\leq \tau_1$에서 $f$는 1차 다항 함수이므로 $f$의 이차, 삼차 미분은 0이어야 한다.
$$\begin{align} f''(x) &= 2b_2
+6b_3x = 0, \forall x\leq \tau_1 \\ f'''(x) &= 6b_3 = 0 \end{align}$$
위를 통하여 $b_2=b_3=0$이어야 하는 것을 알 수 있다.
다음으로 $x\geq \tau_K$에 대해서도 다음을 알 수 있다.
$$(x-\tau_j)^3_+ = (x-\tau_j)^3, j=1, \ldots, K$$
따라서
$$\begin{align} f(x) &= b_0+b_1x + \sum_{j=1}^K\theta_k \left \{ x^3-3x^2\tau_j+3x\tau_j^2-\tau_j^3 \right \} \\ &= b_0-\sum_{j=1}^K\theta_j\tau_j^3 + \left ( b_1+3\sum_{j=1}^K\theta_j\tau_j^2 \right )x - \left ( 3\sum_{j=1}^K\theta_j\tau_j \right )x^2+\left( \sum_{j=1}^K\theta_j \right) x^3 \end{align}$$
앞에서와 마찬가지로 이차항과 삼차항의 계수는 0이 되어야 하므로
$$\sum_{j=1}^K\theta_j=0, \sum_{j=1}^K\theta_j\tau_j=0$$
이 만족되어야 함을 알 수 있다.
(2.9)를 만족하는 (2.5)와 (2.11)의 기저 함수(Basis)는 동일하다.
$f$를 두 Basis로 표현해 보자.
$$f(x) = b_1B_1(x)+b_2B_2(x)+\sum_{j=1}^K\theta_jB_{j+2}(x),\\ \text{where}\;\; B_1(x)=1, B_2(x), B_{j+2}(x) = (x-\tau_j)^3_+, j=1, \ldots, K, \\ \sum_{j=1}^K\theta_j\tau_j=0, \sum_{j=1}^K\theta_j=0 , \tag{B}$$
$$f(x) = a_1N_1(x)+a_2N_2(x)+\sum_{j=1}^{K-2}a_{j+2}N_j(x)\tag{N}$$
이제 (N)과 (B)가 동치인 것을 보이면 된다.
(N) $\Rightarrow$ (B)
$b_1 = a_1, b_2 = a_2$로 먼저 설정한다.
$$\begin{align} \sum_{j=1}^{K-2} a_jN_j(x) &= \sum_{j=1}^{K-2}a_{j+2} (d_j(x)-d_{K-1}(x)) \\ &= \sum_{j=1}^{K-2}a_{j+2} \left \{ \frac{(x-\tau_j)^3_+-(x-\tau_K)^3_+}{\tau_K-\tau_j} - \frac{(x-\tau_{K-1})^3_+-(x-\tau_K)^3_+}{\tau_K-\tau_{K-1}} \right \} \\&= \sum_{j=1}^{K-2}\frac{a_{j+2}}{\tau_K-\tau_j}(x-\tau_j)^3_++\sum_{j=1}^{K-2}\frac{-a_{j+2}}{\tau_K-\tau_{K-1}}(x-\tau_{K-1})^3_+\\ &+\sum_{j=1}^{K-2}a_{j+2}\left ( \frac{-1}{\tau_K-\tau_j} +\frac{1}{\tau_K-\tau_{K-1}} \right )(x-\tau_K)^3_+ \end{align}$$
이때 아래와 같이 설정한다.
$$\theta_j = \frac{a_{j+2}}{\tau_K-\tau_j}, \theta_{K-1} = \sum_{j=1}^{K-2}\frac{-a_{j+2}}{\tau_K-\tau_{K-1}}, \\ \theta_K = \sum_{j=1}^{K-2}a_{j+2}\left ( \frac{-1}{\tau_K-\tau_j} +\frac{1}{\tau_K-\tau_{K-1}} \right )$$
그렇다면
$$f(x) = b_1B_1(x)+b_2B_2(x)+\sum_{j=1}^K\theta_jB_{j+2}(x)$$
임을 알 수 있다. 이때 (B)의 조건식을 만족하는지 확인해야 한다.
$$\begin{align} \sum_{j=1}^K\theta_j &= \sum_{j=1}^{K-2}\theta_j + \theta_{K-1} +\theta_{K} \\ &= \sum_{j=1}^{K-2}\frac{a_{j+2}}{\tau_K-\tau_j}+ \sum_{j=1}^{K-2}\frac{-a_{j+2}}{\tau_K-\tau_{K-1}} + \sum_{j=1}^{K-2}a_{j+2}\left ( \frac{-1}{\tau_K-\tau_j} +\frac{1}{\tau_K-\tau_{K-1}} \right ) \\ &= 0\end{align}$$
$$\begin{align} \sum_{j=1}^K\theta_j\tau_j &= \sum_{j=1}^{K-2}\theta_j\tau_j + \theta_{K-1}\tau_{K-1} +\theta_{K}\tau_K \\ &= \sum_{j=1}^{K-2} \left \{ \frac{a_{j+2}\tau_j}{\tau_K-\tau_j}+ \frac{-a_{j+2}\tau_{K-1}}{\tau_K-\tau_{K-1}} -\frac{a_{j+2}\tau_K}{\tau_K-\tau_j} +\frac{a_{j+2}\tau_K}{\tau_K-\tau_{K-1}}\right \} \\ &= \sum_{j=1}^{K-2}\left \{ \frac{a_{j+2}(\tau_K-\tau_{K-1})}{\tau_K-\tau_{K-1}} - \frac{a_{j+2}(\tau_K-\tau_{j})}{\tau_K-\tau_{j}} \right \} \\ &= \sum_{j=1}^{K-2}(a_{j+2}-a_{j+2}) \\ &= 0 \end{align}$$
(B) $\Rightarrow$ (N)
$f$가 (B)를 만족한다고 하자.
이때 $a_1 = b_1, a_2 = b_2$라 하고 $a_{j+2} = (\tau_K-\tau_j)\theta_j, j=1, \ldots, K-2$라 하자. 이 경우 우리가 보여야 할 것은 다음과 같다.
$$ a_1N_1(x)+a_2N_2(x)+\sum_{j=1}^{K-2}a_{j+2}N_{j+2}(x) = b_1B_1(x)+b_2B_2(x)+\sum_{j=1}^K\theta_jB_{j+2}(x) \tag{*}$$
먼저 ($*$)에서 왼쪽 3번째 항을 파헤쳐보자.
$$\begin{align}& \sum_{j=1}^{K-2}(\tau_K-\tau_j)\theta_jN_{j+2}(x) \\ &= \sum_{j=1}^{K-2}(\tau_K-\tau_j)\theta_j(d_j(x)-d_{K-1}(x)) \\ &= \sum_{j=1}^{K-2}(\tau_k-\tau_j)\theta_j \left \{ \frac{(x-\tau_j)^3+-(x-\tau_K)^3_+}{\tau_k-\tau_j}-\frac{(x-\tau_{K-1})^3_+-(x-\tau_K)^3_+}{\tau_K-\tau_{K-1}} \right \} \\ &= \sum_{j=1}^{K-2}\theta_j \left \{ (x-\tau_j)^3_+-(x-\tau_K)^3_+ \right \} - \sum_{j=1}^{K-2}\frac{(\tau_K-\tau_j)\theta_j}{\tau_K-\tau_{K-1}} \left \{ (x-\tau_{K-1})^3_+-(x-\tau_K)^3_+ \right \} \\ &= \sum_{j=1}^{K-2}\theta_j \left \{ (x-\tau_j)^3_+-(x-\tau_K)^3_+ \right \} + \frac{(\tau_K-\tau_{K-1})\theta_{K-1}}{\tau_K-\tau_{K-1}} \left \{ (x-\tau_{K-1})^3_+-(x-\tau_K)^3_+ \right \} \\ &= \sum_{j=1}^{K-2}\theta_j \left \{ (x-\tau_j)^3_+-(x-\tau_K)^3_+ \right \} +\theta_{K-1} \left \{ (x-\tau_{K-1})^3_+-(x-\tau_K)^3_+ \right \} \\ &= \sum_{j=1}^{K-1}\theta_j(x-\tau_j)^3_+-\left ( \sum_{j=1}^{K-1}\theta_j \right) (x-\tau_k)^3_+ \\ &= \sum_{j=1}^K\theta_j(x-\tau_j)^3_+\end{align}$$
따라서 ($*$)이 성립한다. 이때 4번째와 등식은
$$\sum_{j=1}^{K-2}\theta_j = -\theta_{K-1} - \theta_K, \sum_{j=1}^{K-2}\theta_j\tau_j = -\theta_{K-1}\tau_{K-1} -\theta_K\tau_K $$
6번째 등식은
$$\sum_{j=1}^{K-1}\theta_j = - \theta_{K}$$
을 이용하였다.
c. Effective Degrees of Freedom과 $\lambda$ 의 선택
(2.12)를 행렬식으로 표현하면 다음과 같다.
$$\begin{align}\boldsymbol{\hat{f}} &= N(N^tN+\lambda \Omega)^{-1}N^ty \\ &= S_{\lambda}y \end{align} \tag{2.13}$$
여기서 $\boldsymbol{\hat{f}} = (\hat{f}(x_1), \ldots, \hat{f}(x_n))^t$
이때 $S_{\lambda}$를 Smoother Matrix라 한다. 그리고 Smoother Matrix의 대각 원소의 합 $\text{trace}(S_{\lambda})$를 Smoothing Spline의 Effective Degrees of Freedom(EDF)이라 한다.
일반적인 선형 회귀 모형에서 변수와 절편항을 합쳐서 $p$개가 있다고 할 때 최소 제곱 추정법을 이용한 적합값 $\bf{\hat{f}}$는 다음과 같다($X^tX$의 역행렬이 존재하는 경우).
$$\boldsymbol{\hat{f}} = X(X^tX)^{-1}X^ty \tag{2.14} $$
이때 $H = X(X^tX)^{-1}X^t$을 Hat Matrix라 하는데 Hat Matrix의 Trace는 다음과 같다.
$$\text{trace}(H) = p$$
즉, Hat Matrix의 Trace는 추정해야 할 모수의 개수와 같으며 이는 회귀 모형의 자유도라 할 수 있다. Smoothing Spline과 일반적인 선형 회귀 모형 모두 적합값이 $y$에 대하여 선형이다. 이때 Hat Matrix를 Smoother Matrix로 취급하여 $\text{trace}(S_{\lambda})$도 Smoothing Spline에서 일종의 자유도로 해석할 수 있다는 것이다.
EDF 정의를 하는 이유는 $\lambda$의 해석을 위해서이다. 주어진 $\lambda$에서는 자유도가 어느 정도인지 다시 말해 실제로 몇 개의 모수를 이용한 선형 회귀 식으로 볼 수 있는지를 해석하고자 한 것이다. 반대로 EDF를 고정시켜 놓고 수치적인 방법으로 $\lambda$를 계산할 수도 있다.
$\lambda$를 선택할 때에는 $\lambda$의 후보군을 설정할 때 EDF를 사용한다. 즉, EDF를 5부터 10까지 자연수 집합으로 설정한 다음 각 EDF에 대응하는 $\lambda$를 후보군으로 설정하는 것이다. 이렇게 해야 특정 변수의 개수를 갖는 회귀 모형과 비교할 수 있고 그 결과를 해석하기 쉬워진다.
$\lambda$의 후보군을 선택했다면 leave-one-out 교차 검증을 이용하여 최적 $\lambda$를 선택한다. 주어진 $\lambda$에 대하여 추정 모형을 $\hat{f}_\lambda$라 할 때 다음을 계산한다.
$$\begin{align} CV(\hat{f}_\lambda) &= \frac{1}{n}\sum_{i=1}^n(y_i-\hat{f}_\lambda^{(-i)}(x_i))^2 \\ &= \frac{1}{n}\sum_{i=1}^n \left ( \frac{y_i - \hat{f}_\lambda(x_i)}{1-S_\lambda(i, i)} \right )^2 \end{align}$$
여기서 $\hat{f}_\lambda^{(-i)}$는 $i$번째 데이터를 제외한 추정 모형이고 $S_\lambda(i, i)$는 Smoother Matrix의 $i$번째 대각 원소이다. 두 번째 등식은 굳이 $n$번의 모형을 새로 추정하지 않고 한 번의 모형 추정만으로 $CV$값을 계산할 수 있음을 뜻한다. 이때 $CV$값을 최소화하는 $\lambda$를 선택한다.
d. 파이썬 예제
이번엔 Smoothing Spline을 파이썬으로 구현해 보자. 아래 SmoothingSpline 클래스는 Natural Cubic Spline을 적합한다. 이 클래스는 평활 모수 $\lambda$를 초기값으로 갖는다.
이 클래스는 매듭점과 다항 차수를 초기값으로 갖는다. 클래스의 구조를 살펴보면 Truncated Power Function을 생성하는 trunc_power 함수, 기저 함수 (2.10)을 생성하는 create_natura_cubic_basis 함수, 이 기저 함수를 기반으로 X 행렬을 만들어주는 make_X_matrix, 벌점항 행렬 $\Omega$를 만드는 make_Omega, 모형을 적합하는 fit, 마지막으로 새로운 데이터에 대해서 예측을 수행하는 predict 메서드로 구성되어 있다.
from scipy.misc import derivative
from scipy.integrate import quad
from scipy.optimize import fsolve
from tqdm import tqdm
from joblib import Parallel, delayed
from functools import reduce
class SmoothingSpline:
def __init__(self, basis_type='natural'):
assert basis_type in ['natural', 'bspline']
assert lamb >= 0
self.lamb = lamb ## lambda
self.dof = None ## Effective
self.basis_type = 'natural' ## basis 타입
self.knots = None ## 매듭점
self.basis = None ## Truncated Power Function Basis 배열
self.X = None ## X matrix
self.Omega = None ## Penalty Matrix
self.coef_ = None ## 회귀 계수
def trunc_power(self, x, p=3): ## Truncated Power Function
return x**p if x>0 else 0
def create_natural_cubic_basis(self): ## Natural Cubic Basis를 생성
knots = self.knots
def d(x, knot, max_knot):
numerator = self.trunc_power(x-knot)-self.trunc_power(x-max_knot)
denominator = max_knot-knot
return numerator/denominator
def n(x, knot, sub_knot, max_knot):
return d(x, knot=knot, max_knot=max_knot) - d(x, knot=sub_knot, max_knot=max_knot)
basis = [lambda x:1, lambda x:x]
max_knot = knots[-1]
sub_knot = knots[-2]
for i in range(len(knots)-2):
knot = knots[i]
n = partial(n, knot=knot, sub_knot=sub_knot, max_knot=max_knot)
basis.append(n)
self.basis = basis
def make_X_matrix(self, array): ## Basis 기반 X matrix 생성
knots = np.sort(np.unique(array))
self.knots = knots
self.create_natural_cubic_basis()
basis = self.basis
basis_type = self.basis_type
X = np.array([[b(x=x) for b in basis] for x in array])
self.X = X
def make_Omega(self, n_jobs=4): ## Penalty Matrix 생성
knots = self.knots
def prod_second_deriv(x, func1, func2, dx=1e-6):
return derivative(func1, x, dx=dx, n=2)*derivative(func2, x, dx=dx, n=2)
basis = self.basis
basis_type = self.basis_type
Omega = np.zeros((len(basis), len(basis)))
if basis_type == 'natural':
target_idx = range(2, len(basis))
else:
pass
def do_job(i, basis, prod_second_deriv, min_knot, max_knot):
results = []
for j in range(i, len(basis)):
integrand = partial(prod_second_deriv, func1 = basis[i], func2 = basis[j])
result, _ = quad(integrand, min_knot, max_knot)
results.append((i, j, result))
return results
with Parallel(n_jobs=n_jobs) as parallel:
results = parallel(delayed(do_job)(i, basis, prod_second_deriv, knots[0], knots[-1]) for i in tqdm(target_idx))
results = [x for x in results if x]
results = reduce(lambda x, y:x+y, results)
for i, j, result in results:
Omega[i][j] = result
Omega = Omega + Omega.T - np.diag(np.diagonal(Omega))
self.Omega = Omega
def fit(self, x, y): ## 모형 적합
self.make_X_matrix(x)
lamb = self.lamb
if lamb > 0:
self.make_Omega()
knots = self.knots
X = self.X
Omega = self.Omega
temp_matrix = np.linalg.inv(X.T.dot(X)+lamb*Omega)
self.dof = np.trace(X.dot(temp_matrix.dot(X.T))) ## 자유도 계산
self.coef_ = temp_matrix.dot(X.T.dot(y)) ## 모형 적합, 회귀 계수 추정
return self
def predict(self, array): ## 예측
basis = self.basis
temp = [self.coef_.dot([b(x=x) for b in basis]) for x in array]
return np.array(temp)
이제 Smoothing Spline을 이용하여 앞에서 이용한 남성 작업자의 임금을 나이로 적합해보고 그 결과를 시각화해 보자. $\Omega$계산이 시간이 좀 걸려서 전체적인 적합시간이 각 반복마다 1분 정도 걸린다.
fig = plt.figure(figsize=(10,6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(x, y, color='k', alpha=0.3)
age_grid = np.arange(df['age'].min(), df['age'].max())
for lamb in [0, 0.1, 10, 100]:
sm_spline = SmoothingSpline(lamb=lamb).fit(x, y)
pred = sm_spline.predict(age_grid)
ax.plot(age_grid, pred, label=f'lambda = {str(lamb)}({sm_spline.dof:.2f})')
ax.set_xlabel('Age')
ax.set_ylabel('Wage')
ax.legend()
plt.show()

위 그림을 살펴보면 $\lambda$가 커질수록 매끄러워진다. 그에 따라 Effective Degree of Freedom(EDF)이 작아지는 것을 알 수 있다. 매끄럽다는 것은 복잡하지 않다는 것이므로 실제 적은 변수를 이용한 것과 같다는 의미이다. 또한 $\lambda=0$인 경우 EDF는 61이며 이는 여기서 사용한 매듭점의 개수와 동일하다.
보통은 $\lambda$가 아니라 EDF를 초기값으로 줘서 이로부터 $\lambda$를 역산해야 하는데 내가 만든 함수에서는 어떤 경우에 $\lambda$가 음수가 나와서 추가하지 않았다. 나중에 기회가 되면 공부해서 만들어봐야지..
4. Penalized B-Spline
이번엔 Penalized B-Spline에 대해 알아보자. (당연하게도) B-Spline이 무엇인지 알아보아야 한다.
1) B-Spline
a. 정의
B-Spline은 B-Spline Basis를 이용하여 만들어낸 함수를 말한다. 이때 B는 Basic을 의미한다. 여기서는 B-Spline 보다는 그 기저 함수인 B-Spline Basis(BB)에 대해서 알아보고자 한다. 이야기할 때에는 원래 있던 매듭점 $\tau_1, \ldots, \tau_K$을 증가시킬 필요가 있다. 그래야 충분한 Basis를 만들어 낼 수 있기 때문이다. 그래서 다음과 같은 세팅을 해둔다.
$$k_1\leq k_2 \leq \cdots \leq k_M \leq \tau_1 \\ k_{j+M} = \tau_j, j=1, \ldots, K \\ \tau_K \leq k_{K+M+1} \leq \cdots \leq k_{K+2M} $$
$i$번째 $m(\leq M)$차 B-Spline Basis는 아래와 같은 재귀식을 이용하여 만들어진다.
$$B_{i,0}(x) = \begin{cases} 1 \;\; \text{if} \;\; k_i \leq x < k_{i+1} \\ 0 \;\; \text{o.w} \end{cases}, i=1, \ldots, K+2M-1$$
$$B_{i, m}(x) = \frac{x-k_i}{k_{i+m-1}-k_i}B_{i, m-1}(x)+\frac{k_{i+m}-x}{k_{i+m}-k_{i+1}}B_{i+1, m-1}(x), \\ i=1, \ldots, K+2M-m, m\geq 1$$
유니크한 BB의 개수는 매듭점 $\tau_j$의 개수 $K$와 차수 $m$에 의하여 결정되며 그 개수는 $m+K-1$이다. 이때 주의할 것은 유니크한 BB의 개수를 계산할 때 매듭점의 개수 $k_j$ 개수 $K+2M$이 아니라 $\tau_j$의 개수 $K$를 고려한다는 것이다. 그러면 $k_j$는 왜 필요한 것인가? 그건 바로 유니크한 BB를 모두 만들어내기 위함이다. $m$차 BB를 만들어내기 위해선 $M=m$으로 설정하고 다음과 같이 매듭점을 증가시킨다(Augmented Knots).
$$k_1=k_2=\cdots=k_M=\tau_1, \\ \tau_K = k_{K+M+1}=\cdots=k_{K+2M}=\tau_1$$
아래 그림은 기존 매듭점 $\tau_1, \tau_2, \tau_3, \tau_4$가 있을 때 유니크한 3차 BB가 만들어지는 과정을 나타낸 것이다. 각 열에서 같은 색으로 표시된 것이 0~3차까지의 유니크한 BB가 된다.

$m$차 BB의 유니크한 원소 $B_{i, 1}(x), \ldots, B_{K+m}(x)$가 결정되었으면 이를 이용하여 Smoothing Spline을 추정하게 된다. 주의해야 할 것은 $m$차 BB만 사용하지 그 이전 차수의 BB는 사용하지 않는다.
B-Spline Basis(BB)와 Truncated Power Basis(TPB)는 서로 표현이 가능하다. 그렇다면 Truncated Power Basis를 사용하면 될걸 B-Spline Basis을 왜 사용하는 걸까? 왜냐하면 계산 상에 이점이 있기 때문이다. B-Spline Basis은 특정 구간에서만 0이 아닌 값을 갖고 밖에서는 0을 갖는 함수들이다. 이러한 구조 때문에 B-Spline Basis를 이용하여 만들어지는 행렬 $B$((2) 참고)는 0을 많이 포함하고 $B^tB$는 특정 밴드 밖 원소는 모두 0이 되는 구조를 갖고 있어서 행렬 계산에 이점이 있다는 것이다.
다만 TPB는 매듭점을 특정할 수 있지만 BB는 하나의 기저함수 서포트에 여러 매듭점이 포함되어 있어 매듭점을 특정할 수 없으며 이는 매듭점을 선택하는 프로세스에서는 치명적인 단점이 될 수 있다.
(2.9)를 만족하는 TPB에 대응되는 Natural Cubic Spline Basis를 만든 것처럼 BB도 새로 만들어줘 하는 건 아닌지에 대해서 궁금해질 수 있다. ESL에 의하면 (2.8)에 벌점항이 매듭점 범위 바깥 부분에서 0이 아닌 미분에 대해서 강한 Penalty를 준다고 한다. 즉, 매듭점 범위 바깥쪽에서 최대한 2차, 3차 미분이 0이 되도록 강제한다는 것이다.
b. 파이썬 예제
파이썬을 이용하여 B-Spline Basis를 만들고 시각화해 보자. 먼저 아래 $B$ 함수는 차수 m, 인덱스 i, 증가된 매듭점 ak를 인자로 설정한 상태에서 입력값 $x$에 대한 $i$ 번째 $m$차 BB값을 계산한다.
def B(x, m, i, ak):
if m == 0:
return 1.0 if ak[i] <= x < ak[i+1] else 0.0
if ak[i+m] == ak[i]:
c1 = 0.0
else:
c1 = (x - ak[i])/(ak[i+m] - ak[i]) * B(x, m-1, i, ak)
if ak[i+m+1] == ak[i+1]:
c2 = 0.0
else:
c2 = (ak[i+m+1] - x)/(ak[i+m+1] - ak[i+1]) * B(x, m-1, i+1, ak)
return c1 + c2
이제 B-Spline Basis를 시각화해보자. 여기서는 0~3차 BB를 그려보았다.
## 시각화해보기
knots = np.array([0, 0.25, 0.5, 0.75, 1]) ## 매듭점
min_x = np.min(knots)
max_x = np.max(knots)
epsilon = 1e-5
knots[-1] = max_x + epsilon ## 매듭점 최대값에서 0이 되는 것을 방지하기 위함
t = np.linspace(np.min(knots),max_x,100, endpoint=True)
fig, axs = plt.subplots(2,2,figsize=(20,6))
fig.set_facecolor('white')
for m in range(4):
col_idx = m%2
row_idx = m//2
ax = axs[row_idx, col_idx]
M = m ## 양쪽에 증가시켜야할 매듭점 개수
## 매듭점 증가시켜야한다.
augmented_knots = np.concatenate([np.ones(M)*np.min(knots), knots, np.ones(M)*np.max(knots)])
for i in range(0, M+len(knots)-1):
partial_bspline = partial(B, m=m, i=i, ak=augmented_knots)
ax.plot(t, [partial_bspline(x) for x in t], label=str(i))
ax.set_title(f'{m} Order BB')
ax.legend()
plt.show()

각 Basis는 특정 구간에서만 0이 아니고 구간 바깥에서는 모두 0이 되는 것을 알 수 있다.
2) Penalized B-Spline
a. 정의
Penalized B-Spline(줄여서 P-Spline 이라고도 한다)은 매듭점 구간(매듭점의 최소값과 최대값 사이)을 등간격으로 나눈 매듭점을 사용하여 추정한 Spline을 말한다.
Smoothing Spline을 추정할 때 유니크한 데이터를 매듭점으로 사용한다는 것을 앞에서 살펴보았다. 하지만 데이터의 개수가 많아지면 유니크한 매듭점도 많아지고 이는 행렬 계산의 불안정성으로 이어진다. 따라서 유니크한 매듭점을 다 쓰는 것이 아니라 등간격(Equi-Distance) 매듭점을 사용하여 Spline을 추정하게 된다.
b. 파이썬 예제
이제 BB를 이용하여 Penalized B-Spline 모형을 적합하는 클래스를 만들어보자. PenalizedBSpline 클래스는 평활 모수 $\lambda$와 BB의 차수를 초기값으로 갖는다. 과정은 앞에서 살펴본 SmoothingSpline 클래스와 동일하나 fit 함수에 등간격으로 재구성할 매듭점 개수 num_knots가 들어갔다는 차이가 있다.
class PenalizedBSpline:
def __init__(self, lamb, m):
assert lamb >= 0
self.lamb = lamb ## lambda
self.m = m ## bb order
self.dof = None ## Effective
self.knots = None ## 매듭점
self.basis = None ## Truncated Power Function Basis 배열
self.X = None ## X matrix
self.Omega = None ## Penalty Matrix
self.coef_ = None ## 회귀 계수
def create_equidistance_knots(self, x_data, num_knots):
return np.linspace(np.min(x_data), np.max(x_data), num_knots)
def create_bspline_basis(self, x_data, num_knots): ## Natural Cubic Basis를 생성
def B(x, m, i, ak):
if m == 0:
return 1.0 if ak[i] <= x < ak[i+1] else 0.0
if ak[i+m] == ak[i]:
c1 = 0.0
else:
c1 = (x - ak[i])/(ak[i+m] - ak[i]) * B(x, m-1, i, ak)
if ak[i+m+1] == ak[i+1]:
c2 = 0.0
else:
c2 = (ak[i+m+1] - x)/(ak[i+m+1] - ak[i+1]) * B(x, m-1, i+1, ak)
return c1 + c2
knots = self.create_equidistance_knots(x_data, num_knots)
epsilon = 1e-5
max_knot = np.max(knots)
knots[-1] = max_knot + epsilon
m = self.m
M = m
augmented_knots = np.concatenate([np.ones(M)*np.min(knots), knots, np.ones(M)*np.max(knots)])
basis = []
for i in range(0, M+len(knots)-1):
partial_bspline = partial(B, m=m, i=i, ak=augmented_knots)
basis.append(partial_bspline)
self.knots = knots
self.basis = basis
def make_X_matrix(self, array, num_knots): ## Basis 기반 X matrix 생성
self.create_bspline_basis(array, num_knots)
basis = self.basis
X = np.array([[b(x=x) for b in basis] for x in array])
self.X = X
def make_Omega(self, n_jobs=4): ## Penalty Matrix 생성
knots = self.knots
def prod_second_deriv(x, func1, func2, dx=1e-6):
return derivative(func1, x, dx=dx, n=2)*derivative(func2, x, dx=dx, n=2)
basis = self.basis
Omega = np.zeros((len(basis), len(basis)))
target_idx = range(len(basis))
def do_job(i, basis, prod_second_deriv, min_knot, max_knot):
results = []
for j in range(i, len(basis)):
integrand = partial(prod_second_deriv, func1 = basis[i], func2 = basis[j])
result, _ = quad(integrand, min_knot, max_knot)
results.append((i, j, result))
return results
with Parallel(n_jobs=n_jobs) as parallel:
results = parallel(delayed(do_job)(i, basis, prod_second_deriv, knots[0], knots[-1]) for i in tqdm(target_idx))
results = [x for x in results if x]
results = reduce(lambda x, y:x+y, results)
for i, j, result in results:
Omega[i][j] = result
Omega = Omega + Omega.T - np.diag(np.diagonal(Omega))
self.Omega = Omega
def fit(self, x, y, num_knots): ## 모형 적합
assert num_knots <= len(np.unique(x))
self.make_X_matrix(x, num_knots)
lamb = self.lamb
if lamb > 0:
self.make_Omega()
Omega = self.Omega
else:
Omega = 0
knots = self.knots
X = self.X
temp_matrix = np.linalg.inv(X.T.dot(X)+lamb*Omega)
self.dof = np.trace(X.dot(temp_matrix.dot(X.T))) ## 자유도 계산
self.coef_ = temp_matrix.dot(X.T.dot(y)) ## 모형 적합, 회귀 계수 추정
return self
def predict(self, array): ## 예측
basis = self.basis
temp = [self.coef_.dot([b(x=x) for b in basis]) for x in array]
return np.array(temp)
이제 Penalized B-Spline 모형을 적합하고 결과를 시각화해 보자. 먼저 등간격 매듭점 개수를 10개로 고정하고 평활 모수 $\lambda$를 변화시켜 가면서 어떤 모형이 나타나는지 살펴보자.
fig = plt.figure(figsize=(10,6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(x, y, color='k', alpha=0.3)
age_grid = np.arange(df['age'].min(), df['age'].max())
for lamb in [0, 0.1, 10, 100]:
sm_spline = PenalizedBSpline(lamb=lamb, m=3).fit(x, y, num_knots=10)
pred = sm_spline.predict(age_grid)
ax.plot(age_grid, pred, label=f'lambda = {str(lamb)}({sm_spline.dof:.2f})')
for k in sm_spline.knots: ## 등간격 매듭점 그리기
ax.axvline(k, linestyle='--', color='b')
ax.set_xlabel('Age')
ax.set_ylabel('Wage')
ax.legend()
plt.show()

나이가 72~80인 구간을 제외하고는 거의 흡사한 모형이 나왔다. 이번엔 $\lambda$=10으로 고정하고 등간격 매듭점 개수를 바꿔가면서 모형을 적합해보았다.
fig = plt.figure(figsize=(10,6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(x, y, color='k', alpha=0.3)
age_grid = np.arange(df['age'].min(), df['age'].max())
for num_knots in [5, 10, 20, 50]:
sm_spline = PenalizedBSpline(lamb=10, m=3).fit(x, y, num_knots=num_knots)
pred = sm_spline.predict(age_grid)
ax.plot(age_grid, pred, label=f'num_knots = {str(num_knots)}({sm_spline.dof:.2f})')
ax.set_xlabel('Age')
ax.set_ylabel('Wage')
ax.legend()
plt.show()

등간격 매듭점의 개수가 커질수록 Eeffective Degree of Freedom도 증가하는 것을 알 수 있으며 모형이 과적합되는 현상이 나타나는 것을 알 수 있다.
4. 장단점
Spline Regression의 장단점은 다음과 같다.
- 장점 -
a. 유연하다!
Spline Regression은 기존 선형 회귀로는 표현이 불가능한 복잡한 비선형 관계를 기저 함수를 이용하여 비교적 쉽게 모델링할 수 있다.
b. 매듭점을 사용하여 적합하지만 평활 모수를 사용하여 전체적으로 매끄러운 곡선도 만들어 낼 수 있다.
- 단점 -
a. 매듭점 개수가 많아지면 계산이 복잡해져 언더플로우 같은 문제가 발생하고 이는 추정치 계산의 신뢰성을 저하시킬 수 있다.
이 경우 등간격 매듭점을 사용하여 매듭점의 수를 줄이기도 한다.
b. 매듭점이 많은 경우 과적합 문제가 발생할 수 있다.
c. 해석이 어렵다.
Spline Regression도 비모수 방법이므로 선형 회귀와 같은 계수의 해석을 기대할 수 없다.
d. 최적 매듭점 선택결과가 민감하다.
최적 매듭점의 선택 결과가 매듭점 집합의 선택에 따라 달라진다.





댓글