이번 포스팅에서는 다변량 분석 기법의 하나인 인자 분석(Factor Analysis)에 대한 개념과 파이썬으로 구현하는 방법에 대해서 알아보고자 한다.
- 목차 -
1. 인자 분석(Factor Analysis)이란?
1) 정의
인자 분석(Factor Analysis)이란 변수들이 갖고 있는 상관 구조를 잠재적인 공통인자를 이용하여 설명하는 다변량 분석 기법이다. 인자 분석에서는 변수와 잠재적인 공통인자 사이의 관계를 나타내는 통계적 모형을 설정하여 변수들 간 상호 관계를 잠재적인 공통인자를 찾아내어 해석한다.
2) 파헤치기
앞에서 정의한 내용을 구체적으로 파헤쳐보자.
a. 인자 분석(Factor Analysis)은 공통 인자를 이용하여 변수들의 상관 구조를 파악하며 공통 인자를 통해 해석 가능한 지표를 만들 수도 있다.
인자 분석은 기본적으로 관측된 변수들의 상관 관계를 관측되지 않은 공통 인자로 설명하는 분석 기법이다.
아래 표는 7개 변수를 2개의 공통 인자를 이용하여 인자 분석을 진행한 결과이다.
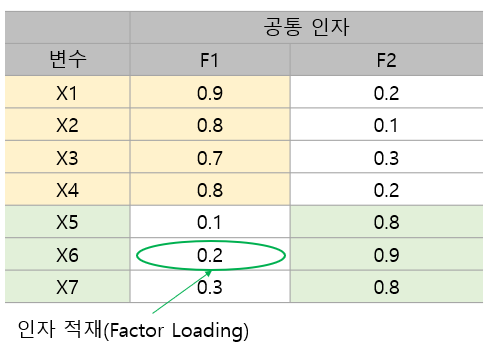
위 표를 보면 변수 X1~X4에 대하여 첫 번째 공통 인자의 값(인자 적재라고 한다)이 크고 나머지 변수 X5~X7에 대해선 작은 것을 알 수 있다. 반면 두 번째 공통 인자 값을 살펴보면 X1~X4에서 작고 나머지 변수 X5~X7에서 큰 것을 알 수 있다. 인자 분석은 위 결과에 대하여 X1~X4가 첫 번째 공통 인자를 통해 비슷한 상관 구조를 갖는 변수 집단, X5~X7은 두 번째 공통 인자를 통해 비슷한 상관 구조를 갖는 변수 집단이라고 해석할 수 있게 해 준다. 아래 그림은 이러한 관계를 나타낸 것이다.

반대로 첫 번째 공통 인자를 X1~X4를 공통적으로 설명할 수 있는 지표, 두 번째 공통 인자를 X5~X7을 공통적으로 설명할 수 있는 지표로도 해석할 수 있다(물론 실제 분석에서는 해석하기가 힘들다).
요약하면 기존에는 관측할 수 없었던 상관 구조를 공통 인자를 통해 찾아낼 수 있게 하고 공통 인자를 해석하여 의미 있는 지표로 활용할 수 있게 하는 것이 인자 분석의 목적인 것이다.
b. 인자 분석은 개별 변수들이 공통 인자의 선형 결합과 공통 인자로 설명되지 않는 부분으로 이루어진 통계적 모형을 가정한다.
인자 분석은 개별 변수들이 공통 인자의 선형 결합과 공통 인자로 설명되지 않는 개별 변수들의 특성으로 이루어진 통계적 모형을 가정한다.

이에 대한 구체적인 내용은 아래에서 구체적으로 다루기로 한다.
2. 인자 분석(Factor Analysis) 방법
1) 모형 설정(직교 인자 모형)
인자 분석은 변수들이 다음과 같이 공통 인자의 선형 결합으로 표현된다고 가정한다.
$X_i- \mu_i = l_{i, 1} f_1 + l_{i, 2}f_2 + \cdots + l_{i, m}f_m +\epsilon_i, i=1, \ldots, p \tag{1}$
여기서
$X_i$는 $i$번째 변수
$\mu_i$는 $i$번째 변수의 평균(기대값)
$l_{i, k}$는 $i$번째 변수의 $k$ 번째 인자 적재(Factor Loading)
$f_k$는 $k$번째 공통 인자(Common Factor)
$\epsilon_i$는 $m$개의 공통 인자가 설명하지 못하는 $i$번째 변수만이 가진 특성 인자(Specific Factor)
(1)을 행렬로 표현하면 다음과 같다.
$$X - \mu = Lf + \epsilon \tag{2}$$
여기서 $X=(X_1, \ldots X_p)^t, \mu = (\mu_1, \ldots, \mu_p)^t, f=(f_1, \ldots, f_m)^t, \epsilon=(\epsilon_1, \ldots, \epsilon_p)^t$이고 $p\times m$ 행렬 $L$은 다음과 같다.
$$L = \begin{pmatrix} l_{11} & l_{12} & \cdots & l_{1m} \\ l_{21} & l_{22} & \cdots & l_{2m} \\ \vdots & \vdots & \ddots & \vdots \\ l_{p1} & l_{p2} & \cdots & l_{pm} \end{pmatrix}$$
이때 $L$을 인자 적재 행렬이라 한다.
인자 분석은 (1)에 대해서 직교 인자 모형을 설정하기 위해 몇 가지 통계적인 가정을 하게 된다.
가정 1)
$$\begin{align} E(F_k) = 0, \text{Var}(F_k)=1, k=1, \ldots, m, \\ \text{Cov}(F_j, F_k) = 0 \;(j\neq k), \;\; j, k = 1, \ldots, m \end{align}$$
가정 2)
$$\begin{align} E(\epsilon_i) = 0, \text{Var}(\epsilon_i)=\psi_i, i=1, \ldots, p, \\ \text{Cov}(\epsilon_i, \epsilon_j) = 0\; (i\neq j), \;\; i, j = 1, \ldots, p \end{align}$$
가정 3)
$$ \text{Cov}(\epsilon_i, f_k) = 0, i=1, \ldots, p, \; k=1, \ldots, m $$
가정 1)은 공통 인자의 평균은 0이고 분산이 1이며 서로 다른 공통 인자들 사이에는 상관성이 없다는 뜻이다. 일반적으로 공통 인자들은 상관성이 있지만 모형의 간편성, 추정에 필요한 계산의 효율성을 위해 이러한 가정을 하는 것이다. 가정 2)는 특성 인자의 평균은 0이고 분산이 개별 변수에 따라 다르며 서로 다른 특성 인자들 간에는 상관성이 없다는 뜻이다. 마지막으로 가정 3)은 공통 인자와 특성 인자간 상관성은 없다는 뜻이다.
가정 1)~3)까지 만족하는 모형을 직교 인자 모형이라 한다.
위 가정들을 이용하여 직교 인자 모형의 성질을 살펴보자.
확률 변수 벡터 $X$의 공분산 행렬을 인자 적재 행렬과 특성 인자의 분산 행렬로 표현할 수 있다.
$$\begin{align} \Sigma &= E(X-\mu)(X-\mu)^t \\ &= E(Lf + \epsilon)(Lf+\epsilon)^t \\ &= E(Lff^tL^t + Lf\epsilon^t + \epsilon f^t L^t + \epsilon \epsilon^t) \\ &= LE(ff^t)L^t + LE(f\epsilon^t) +E(\epsilon f^t)L^t +E(\epsilon \epsilon^t) \\ &= LL^t +\psi \end{align} \tag{3}$$
여기서 $$\psi = \begin{pmatrix} \psi_{1} & 0 & \cdots & 0 \\ 0 & \psi_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \psi_p \end{pmatrix} $$
이다.
그리고 $X$와 공통 인자 벡터 $f$의 공분산 행렬은
$$\begin{align} \text{Cov}(X, f) &= E[(X-\mu)f^t] \\ &= E[(Lf+\epsilon)f^t] \\ &= LE(ff^t)+E(\epsilon f^t) = L \end{align} \tag{4}$$
(3)에 의하여 $X_i$의 분산을 다음과 같이 인자 적재와 특성 인자의 분산으로 표현된다는 것을 알 수 있다.
$$ \text{Var}(X_i) = l_{i1}^2+l_{i2}^2 + \cdots + l_{im}^2 + \psi_i = \sum_{j=1}^m l_{ij}^2+\psi_i \\ \text{Cov}(X_i, X_k) = l_{i1}l_{k1} +l_{i2}l_{k2} + \cdots + l_{im}l_{km} = \sum_{j=1}^m l_{ij}l_{kj} \tag{5}$$
(4)에 의하여 다음을 알 수 있다.
$$\text{Cov}(X_i, f_j) = l_{ij}\tag{6}$$
(5)에서 $X_i$의 분산 중에서 공통 인자에 의하여 설명되는 부분을 $h_i^2$로 표시하며 이를 공통성(Communality)라 한다. 그리고 $\psi_i$은 공통 인자가 설명할 수 없고 특정 인자에 의하여 설명되는 부분을 특정 분산(Specific Variance)이라 부른다.
따라서 (5)를 다시 쓰면 다음과 같다.
$$\text{Var}(X_i) = l_{i1}^2+l_{i2}^2+\cdots +l_{im}^2+\psi_i = h_i^2+\psi_i \tag{7}$$
이때 2가지 분산 설명 비율을 정의할 수 있다. 첫 번째는 $m$개의 전체 분산이 공통 인자에 의하여 설명되는 분산 비율로써 다음과 같이 정의한다.
$$ \frac{\sum_{i=1}^p h_i^2}{\sum_{i=1}^p\sigma_i^2} \tag{8}$$
그리고 전체 분산이 $j$ 번째 공통 인자 $f_j$에 의하여 설명되는 분산 비율은 다음과 같이 정의한다.
$$\frac{\sum_{i=1}^pl_{ij}}{\sum_{i=1}^p\sigma_i^2} \tag{9}$$
모든 $i=1, \ldots, p$에 대하여 $0\leq h_i^2 \leq \sigma_i^2, 0\leq l_{ij} \leq \sigma_i^2 $이므로 (8)과 (9)는 모두 0과 1 사이의 값을 가지므로 비율로 해석할 수 있게 된다. 만약 (8)의 값이 1에 가깝다면 공통 인자에 의하여 전체 분산이 잘 설명된다는 것이며 이는 $m$개의 공통 인자 만으로도 자료를 잘 요약한다는 것을 의미한다. 만약 0에 가깝다면 변수들이 공통 인자에 의하여 거의 설명될 수 없음을 의미한다. (9)도 비슷한 해석을 할 수 있다.
(8)은 $m$개의 전체 분산이 공통 인자에 의하여 설명되는 분산 비율이며 이는 공통 인자의 수를 정하는 기준으로도 활용될 수 있다. (9)는 개별 공통 인자에 의하여 설명되는 분산 비율이며 이는 자료를 잘 요약하는 정도를 나타내며 이는 공통 인자를 선별하는 기준으로 활용될 수 있다.
2) 인자 적재 행렬 추정 방법
인자 적재 행렬은 여러 가지 방법으로 추정할 수 있다. 여기서는 주성분 방법(Principal Component Method), 주인자 방법(Principal Factor Method) 그리고 최대 우도 추정법(Maximum Likelihood)으로 추정하는 방법이 있다. 이에 대해서 각각 알아보자.
a. 주성분 방법(Principal Component Method)
주성분 방법에서는 공분산 행렬을 고유값 분해했을 때 몇 개의 주성분을 이용하여 인자 적재 행렬을 추정하는 방법이다. 구체적으로 알아보자.
먼저 변수들이 평균이 0, 분산이 1이라고 가정한다(표준화된 것이다). 그렇다면 변수들의 공분산 행렬은 상관 행렬 $\rho$가 된다. 이를 인자 적재 행렬과 특정 분산 행렬로 표시하면 다음과 같다.
$$\rho = LL^t+\psi\tag{10}$$
주성분 방법에서는 인자 적재 행렬을 이용하여 상관 행렬 $\rho$를 대부분 설명할 수 있다고 가정한다. 이는 곧 $\psi$의 대각 원소들이 무시할 수 있을 정도로 작다는 것과 같은 것이다. 따라서 상관 행렬은 다음과 같이 근사하게 된다.
$$\rho \approx LL^t$$
이제 $\rho$의 고유값 분해식이 다음과 같다고 해보자.
$$\rho = \lambda_1 v_1v_1^t+\lambda_2 v_2v_2^t + \cdots + \lambda_pv_pv_p^t \tag{11} $$
만약 $\rho$가 처음 $m$개 주성분에 의하여 변수들의 분산 구조가 대부분 설명된다고 가정하면 나머지 $p-m$개의 고유값 $\lambda_{p-m+1}, \ldots, \lambda_{p}$는 매우 작기 때문에 (11)에서 제외할 수 있으며 상관 행렬 $\rho$는 다음과 같이 근사하게 되며 이를 인자 적재 행렬로 추정하게 되는 것이다.
$$ \begin{align}\rho & \approx \lambda_1 v_1v_1^t+\lambda_2 v_2v_2^t + \cdots + \lambda_mv_mv_m^t \\ &= \left ( \sqrt{\lambda_1}v_1 \sqrt{\lambda_2}v_2 \ldots, \sqrt{\lambda_m}v_m \right ) \begin{pmatrix} \sqrt{\lambda_1} v_1^t \\ \sqrt{\lambda_2} v_2^t \\ \vdots \\ \sqrt{\lambda_m} v_m^t \end{pmatrix} \\ &= LL^t \end{align} $$
이때 인자 적재 행렬 $L$은 다음과 같이 추정하는 것이다.
$$L = \left ( \sqrt{\lambda_1}v_1 \sqrt{\lambda_2}v_2 \ldots, \sqrt{\lambda_m}v_m \right )$$
물론 추정은 표본을 이용하여 추정하므로 $\rho$의 추정량인 표본 상관 행렬 $R$을 고유값 분해하여 인자 적재 행렬을 추정하게 된다.
주성분 방법에서 스크리 도표(Scree Plot)을 이용하여 분산 설명 비율의 증가폭이 현저히 낮아지는 지점까지의 주성분으로 공통 인자의 수를 정하게 된다.
b. 주인자 방법(Principal Factor Method)
주성분 방법에서는 특정 분산 행렬 $\psi$를 무시했지만 주인자 방법은 $\psi$를 반영하여 인자 적재 행렬을 반복적인 수치 알고리즘을 이용하여 추정하는 방법이다.
여기서도 변수들은 표준화되어 있다고 가정한다.
(10)을 다시 정리하면 다음과 같다.
$$\rho - \psi = LL^t \tag{12}$$
(12)의 좌변을 행렬로 다시 쓰면 다음과 같다.
$$\begin{align} \rho-\psi &= \begin{pmatrix} 1-\psi_1 & r_{12} & \cdots & r_{1p} \\ r_{21} & 1-\psi_2 & \cdots & r_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ r_{p1} & r_{p2} & \cdots & 1-\psi_p \end{pmatrix} \\ &= \begin{pmatrix} h_1^2 & r_{12} & \cdots & r_{1p} \\ r_{21} & h_2^2 & \cdots & r_{2p} \\ \vdots & \vdots & \ddots & \vdots \\ r_{p1} & r_{p2} & \cdots & h_p^2 \end{pmatrix} \end{align} \tag{13} $$
위에서 두 번째 등호는 (7)과 표준화된 변수의 분산은 1이므로 성립한다.
주성분 분석은 상관 행렬 자체를 이용했다면 주인자 방법은 상관 행렬의 대각 원소를 공통성으로 대체한 행렬을 이용한다.
주인자 방법에서 인자 적재 행렬 추정 알고리즘은 다음과 같다.
알고리즘 1
1 단계) 초기 공통성 $h_i^{2(0)} = 1-1/r_{ii}$로 설정한 뒤 (13)에 넣어준 행렬을 $R^{(0)}$으로 설정한다. 여기서 $r_{ii}$는 표본 상관 행렬의 역행렬 $R^{-1}$의 $i$번째 대각 원소이다. 그리고 오차 한계 $\epsilon$을 설정한다.
$l = 1, 2, \ldots$에 대하여 2~4 단계)를 반복한다.
2 단계) $R^{(l-1)}$을 고유값 분해를 이용하여 다음과 같이 근사한다.
$$R^{(l-1)} \approx L^{(l-1)}L^{t(l-1)}$$
위에서 고유값이 양수인 것 고유값과 고유 벡터로 근사한다.
$L^{(l-1)}$을 이용하여 공통성 $h_i^{2(l)}$을 계산한다.
3 단계) $h_i^{2(l)}$를 (13)에 대체한 행렬 $R^{(l)}$과 이를 이용한 인자 적재 행렬 $L^{(l)}$을 2 단계)에서와 같은 방법으로 계산한다.
4 단계) $\sum_{i=1}^p (h_i^{2(l)} - h_i^{2(l-1)})^2 < \epsilon$이면 반복을 중단하고 아닌 경우에는
$R^{(l-1)} \leftarrow R^{(l)}, L^{(l-1)} \leftarrow L^{(l)}$로 설정한 뒤 2 단계)로 돌아간다.
알고리즘 1은 수렴성은 보장되지 않는 것 같다(참고 자료).
알고리즘 1 단계)에서 공통성의 초기값은 $i$번째 변수를 나머지 $p-1$개의 변수를 이용하여 선형 회귀 모형으로 추정한 경우의 다중 상관 계수의 제곱을 의미하며 이는 개별 변수에 대하여 나머지 변수들을 공통 인자로 사용했을 때 공통성을 의미한다. 그 이유를 알아보자.
$p$ 번째 변수 $X_p$를 종속 변수로하고 나머지 변수를 독립변수로 하는 선형 회귀 모형에서 $X_p$의 추정치를 $\hat{X}_p$라 할 때 다음을 증명할 것이다.
$$1-\frac{1}{r_{pp}} = \text{Corr}(\hat{X}_p, X_p)^2 $$
표본 상관 행렬 $R$에서 임의의 $i$ 번째 행을 맨 마지막으로 보낸다고 생각하면 되므로 위를 증명하는 것만으로도 충분하다. 표본 상관 행렬을 다음과 같이 분할한다.
$$R =\begin{pmatrix} A & b \\ b^t & 1 \end{pmatrix} $$
여기서 $A$는 $X_1, \ldots, X_{p-1}$의 표본 상관 행렬이 되고 $b$는 $X_p$와 나머지 변수들 간의 표본 상관 계수를 원소로하는 벡터가 되며 1은 말 그대로 진짜 숫자를 의미한다. 분할 행렬의 역행렬 공식을 이용하면 다음을 알 수 있다.
$$r_{pp}^{-1} = (1-b^tA^{-1}b)^{-1} \Rightarrow 1-\frac{1}{r_{pp}} = b^tA^{-1}b \tag{14}$$
이때 $X_p$를 나머지 변수를 이용하여 선형 회귀 모형을 추정했을 때 회귀 계수 벡터 $\hat{\beta}$는 다음과 같이 계산 된다.
$$\hat{\beta} = (X_{-p}^tX_{-p})^{-1}X_{-p}^tX_{p} $$
여기서 $X_{-p}$는 $p$를 제외한 나머지 변수들을 칼럼 벡터로 하는 설계 행렬이다(행은 관측치를 나타낸 것이라 생각하자). 그렇다면 다음을 알 수 있다. 그리고 변수들은 표준화 되어 있으므로 $A = X_{-p}^tX_{-p}$이고 $b = X_{-p}^tX_{p}$이다. 이제 (14)를 정리해보자.
$$\begin{align}b^tA^{-1}b &= X_{p}^tX_{-p} (X_{-p}^tX_{-p})^{-1}X_{-p}^tX_{p} \end{align} \tag{15}$$
이때
$$\begin{align}\text{Cov}(\hat{X}_p, X_p) &= \left ( X_{-p}(X_{-p}^tX_{-p})^{-1}X_{-p}^tX_{p} \right )^t X_p \\ &= X_{p}^tX_{-p} (X_{-p}^tX_{-p})^{-1}X_{-p}^tX_{p} \end{align} \tag{16}$$
또한
$$\begin{align}\text{Var}(\hat{X}_p) &= \left ( X_{-p}(X_{-p}^tX_{-p})^{-1}X_{-p}^tX_{p} \right )^t \left ( X_{-p}(X_{-p}^tX_{-p})^{-1}X_{-p}^tX_{p} \right ) \\ &= X_{p}^tX_{-p} (X_{-p}^tX_{-p})^{-1}X_{-p}^tX_{p} \end{align} \tag{17}$$
따라서 (16), (17)을 이용하면 다음을 알 수 있다.
$$ 1-\frac{1}{r_{pp}} = b^tA^{-1}b = \text{Cov}(\hat{X}_p, X_p) = \text{Var}(\hat{X}_p) $$
이제 $\hat{X}_p$와 $X_p$의 다중 상관 계수 $\text{Corr}(\hat{X}_p, X_p)$는 다음과 같다.
$$\text{Corr}(\hat{X}_p, X_p) = \frac{\text{Cov}(\hat{X}_p, X_p)}{\sqrt{\text{Var}(\hat{X}_p)}} = \sqrt{\text{Cov}(\hat{X}_p, X_p)} = \sqrt{1-\frac{1}{r_{pp}}}$$
c. 최대 우도 추정법(Maximum Likelihood)
(1) 최대 우도 추정량 계산
최대 우도 추정법은 $p$차원 확률 변수 벡터 $X$가 $p$ 차원 다변량 정규분포를 따른다는 가정을 할 수 있는 경우에 인자 적재 행렬을 추정하는 방법이다.
$p$차원 정규분포 $N_p(\mu, \Sigma)$에서 독립적으로 추출된 확률 표본을 $X_i, i=1, \ldots, n$이라할 때 $X_i = LF_i + \epsilon_i$로 표현할 수 있다. 이제 우도 함수를 계산해 보자.
$$\begin{align} & f(x_1, x_2, \ldots, x_n) \\ &= \prod_{i=1}^nf(x_i) \\ &= (2\pi)^{-\frac{np}{2}}|\Sigma|^{-\frac{n}{2}} \exp \left \{ -\frac{1}{2} \sum_{i=1}^n(x_i-\mu)^t\Sigma^{-1} (x_i-\mu) \right \} \\ &= (2\pi)^{-\frac{np}{2}}|\Sigma|^{-\frac{n}{2}} \exp \left [ -\frac{1}{2} \text{tr} \left \{ \sum_{i=1}^n(x_i-\mu)^t\Sigma^{-1} (x_i-\mu) \right \} \right ] \\ &= (2\pi)^{-\frac{np}{2}}|\Sigma|^{-\frac{n}{2}} \exp \left [ -\frac{1}{2} \text{tr} \left \{ \Sigma^{-1} \sum_{i=1}^n (x_i-\mu) (x_i-\mu)^t\right \} \right ] \\ &= (2\pi)^{-\frac{np}{2}}|\Sigma|^{-\frac{n}{2}} \exp \left [ -\frac{n}{2} \text{tr} \left \{ \Sigma^{-1} S + (\bar{x} - \mu)(\bar{x}-\mu)^t \right \} \right ] \end{align} \tag{18}$$
여기서 $S = \sum_{i=1}^n(x_i-\bar{x})(x_i-\bar{x})^t/n$이다.
최대 우도 추정법을 이용하여 추정해야 할 모수는 $L, \psi$이므로 이것과 관련 없는 항은 제외하고 (18) 양변에 로그를 취해서 정리하면 다음과 같다.
$$\begin{align} \log \text{L} (L, \psi) &= l(L, \psi) \\ &= -\frac{1}{2} n \left [ \log |\Sigma| + \text{tr} (\Sigma^{-1}S) \right ] \\ &= -\frac{1}{2} n \left [ \log |LL^t+\psi| + \text{tr} \left \{ (LL^t+\psi)^{-1}S \right \} \right ] \end{align}\tag{19}$$
(19)에서 로그 우도 함수 $l$을 $L$과 $\psi$에 대하여 편미분하고 이를 0으로 하는 것이 바로 $L, \psi$의 최대 우도 추정량이다. Joreskog는 1966년 "Some Contributions to Maximum Likelihood Factor Analysis"에서 $L, \psi$를 동시에 추정하는 것이 아닌 $\psi$가 주어진 상황에서 $L$을 추정하고 이를 통하여 $\psi$를 다시 업데이트하는 방법으로 최대 우도 추정량을 계산하는 방법을 제안하였다. 이에 대해서 알아보자.
먼저 $\psi$가 주어졌다고 해보자. Joreskog는 (19)를 최대화하는 문제를 아래의 목적함수를 최소화하는 문제로 전환하였다.
$$ f(L, \psi) = \log | \Sigma| +\text{tr}(\Sigma^{-1}) -\log |S| - p \tag{20} $$
(20)의 좌변에서 첫 번째, 두 번째 항은 (19)에서 음수인 상수를 제외한 것이고 나머지 항은 $L, \psi$와 관련이 없으므로 (19)를 최대화하는 것은 (20)을 최대화하는 것과 같다. 이렇게 바꿔준 이유는 $f$의 최소값을 계산할 때 식이 단순해지기 때문이다.
이제 최대 우도 추정량 $L$을 계산하기 위해 $f$를 $L$에 대해서 미분해야 한다. 행렬 미분과 연쇄 법칙을 사용하면 다음을 알 수 있다.
$$\begin{align}\frac{d \log |\Sigma|}{dL} &= (\Sigma^{-1}) (2L) = 2\Sigma^{-1}L \\ \frac{d\text{tr}(\Sigma^{-1}S)}{dL} &=\left ( \Sigma^{-1}S\Sigma^{-1} \right ) (2L) = 2 \Sigma^{-1}S\Sigma^{-1}L\end{align}$$
이를 이용하면
$$\frac{df}{dL} = 2\Sigma^{-1}(\Sigma - S)\Sigma^{-1}L$$
임을 알 수 있다. 이를 0으로 두고 $\Sigma$를 왼쪽에 곱해주면 다음을 알 수 있다.
$$ (\Sigma - S)\Sigma^{-1}L = 0 \tag{20}$$
그리고 $(A-BD^{-1}C)^{-1} = A^{-1}+A^{-1}B(D-CA^{-1}B)^{-1}CA^{-1}$를 이용하면 다음을 알 수 있다.
$$\Sigma^{-1} = (\psi - L(-I)L^t)^{-1} = \psi^{-1} - \psi^{-1}L (I+L^t\psi^{-1}L)^{-1}L^t\psi^{-1}\tag{21}$$
(21)을 이용하면 (20)을 다음과 같이 정리할 수 있다.
$$\begin{align} (\Sigma - S)\Sigma^{-1}L &= (\Sigma - S)\left \{ \psi^{-1} - \psi^{-1}L (I+L^t\psi^{-1}L)^{-1}L^t\psi^{-1} \right \} L \\ &= (\Sigma - S)\left \{ \psi^{-1}L - \psi^{-1}L (I+L^t\psi^{-1}L)^{-1}L^t\psi^{-1}L \right \} \\ &= (\Sigma - S)\left \{ \psi^{-1}L (I -(I+L^t\psi^{-1}L)^{-1}L^t\psi^{-1}L) \right \} \\ &= (\Sigma - S)\psi^{-1}L (I+L^t\psi^{-1}L)^{-1} \end{align}$$
마지막 등식은
$$ \begin{align} & I -(I+L^t\psi^{-1}L)^{-1}L^t\psi^{-1}L \\ &= (I+L^t\psi^{-1}L)^{-1}(I+L^t\psi^{-1}L) -(I+L^t\psi^{-1}L)^{-1}L^t\psi^{-1}L \\ &= (I+L^t\psi^{-1}L)^{-1}((I+L^t\psi^{-1}L)- L^t\psi^{-1}L) \\ &= (I+L^t\psi^{-1}L)^{-1} \end{align}$$
이므로 성립한다.
위 사실을 이용하면 (20)은 다음과 같이 쓸 수 있다.
$$(\Sigma - S)\psi^{-1}L (I+L^t\psi^{-1}L)^{-1} = 0$$
위 식에서 $ (I+L^t\psi^{-1}L)$을 양변 오른쪽에 곱해주면 다음 식을 얻을 수 있다.
$$(\Sigma - S)\psi^{-1}L = 0 \tag{22}$$
(3)을 (22) 넣고 정리하면 다음과 같다.
$$S\psi^{-1}L = L(I+L^t\psi^{-1}L)$$
위에서 양변 왼쪽에 $\psi^{-\frac{1}{2}}$을 곱해주면
$$ \psi^{-\frac{1}{2}}S \psi^{-\frac{1}{2}} (\psi^{-\frac{1}{2}} L) = (\psi^{-\frac{1}{2}}L)(I+L^t\psi^{-1}L)\tag{23}$$
만약 $L^t\psi^{-1}L$이 대각 행렬 $\Delta$라는 제약 조건이 추가되면 $\psi^{-\frac{1}{2}}L$의 칼럼 벡터는 $\psi^{-\frac{1}{2}} S \psi^{-\frac{1}{2}}$의 고유 벡터의 비례하는 것을 알 수 있으며 해당 고유값은 I+\Delta의 대각 원소가 된다. 또한 $\psi^{-\frac{1}{2}}L$의 칼럼 벡터의 길이의 제곱은 $ \psi^{-\frac{1}{2}} S \psi^{-\frac{1}{2}}=\Delta$의 대각 원소가 된다. $\psi^{-\frac{1}{2}} S \psi^{-\frac{1}{2}}$의 고유값을 내림차순으로 정렬했을 때 처음 $m$개의 고유값을 대각 원소로 하는 행렬을 $\Lambda$, 이에 해당하는 고유 벡터를 칼럼으로 하는 행렬을 $E$라 하자. 그러면 앞에서 발견한 사실을 통해 $\psi^{-\frac{1}{2}}L$을 다음과 같이 표현할 수 있다.
$$ \psi^{-\frac{1}{2}}L = E(\Delta)^{\frac{1}{2}} = E(\Lambda - I)^{\frac{1}{2}} $$
그리고 위 식 양변 왼쪽에 $\psi^{\frac{1}{2}}$을 곱해주면 다음을 알 수 있다.
$$ L =\psi^{\frac{1}{2}}E(\Lambda - I)^{\frac{1}{2}}\tag{23} $$
이렇게 구한 $L$을 $f(L, \psi)$에 집어넣은 것을 $f_L(\psi)$라 하면 $f_L$을 최소화하는 $\psi$를 찾아서 기존 $\psi$를 업데이트하는 것이다. 이렇게 업데이트된 $\psi$를 이용하여 (23)을 통해 $L$을 업데이트 하는 것이다. 이때 Joreskog는 $\psi$를 업데이트할 때 Fletcher와 Powell의 수치 알고리즘을 사용했다고 한다.
여기서 문제가 되는 것은 $\psi^{-\frac{1}{2}} S \psi^{-\frac{1}{2}}$의 고유값이 1보다 작은 경우에는 (23)이 만족되지 않으므로 $\Lambda, E$는 반드시 1보다 큰 고유값과 이에 해당하는 고유 벡터로 만들어야 한다는 것이다.
이제 인자 적재 행렬 $L$의 최대 우도 추정량 알고리즘을 요약하면 다음과 같다.
알고리즘 2
1 단계) 오차 한계 $\epsilon$과 초기 $\psi^{(0)}$을 설정한다. Joreskog는 다음과 같은 초기값을 제안하였다. $\psi$의 $i$ 번째 대각 원소$\psi_{i}$에 대하여
$$\psi_{i} = \left ( 1- \frac{m}{2p} \right )\cdot \frac{1}{s_{ii}} \;\; i=1, \ldots, p$$
여기서 $m$은 공통 인자 개수, $p$는 변수 개수이고 $s_{ii}$는 표본 상관 행렬의 역행렬의 $i$번째 대각 원소이다. $m$은 주성분 방법에서 설정한 $m$을 초기 $m$으로 설정한다.
$l=1, 2, \ldots$에 대해서 다음을 반복한다.
2 단계) $(\psi^{(l-1)})^{-\frac{1}{2}} S (\psi^{(l-1)})^{-\frac{1}{2}}$의 고유값을 내림차순으로 정렬했을 때 1보다큰 고유값(편의상 1보다 큰 고유값의 개수를 $m$이라 하겠다. 물론 매 반복마다 $m$값은 달라진다)을 $\lambda_1 > \lambda_2 > \cdots > \lambda_m \geq 1$이라 하자. 해당 고유값을 대각 원소로 하는 대각 행렬 $\Lambda = \text{diag}(\lambda_1, \lambda_2, \ldots, \lambda_m)$이라 하고 이에 대응하는 고유 벡터를 칼럼으로 하는 행렬을 $E$라 하자. 이때 $L^{(l)}$을 다음과 같이 계산한다.
$$L^{(l)} =(\psi^{(l-1)})^{-\frac{1}{2}} E(\Lambda - I)^{\frac{1}{2}}$$
3 단계) $L^{(l)}$을 $f(L, \psi)$에 넣고 $f_{L^{(l)}}$을 최소화하는 $\psi^{(l)}$을 찾는다. 이때 $\psi^{(l)}$의 원소는 모두 양수여야하지만 (초기값의 설정 또는 표본의 개수가 적은 문제로 인하여) 어떤 원소는 음수가 나오는 경우가 있다(이러한 현상을 Heywood 상황이라 한다). 이때에는 해당 원소를 작은 양수로 대체한다.
4 단계) $\| \psi^{(l)} - \psi^{(l-1)} \|_2 < \epsilon$이면 알고리즘을 종료하고 아니면 $\psi^{(l-1)} \longleftarrow \psi^{(l)}$으로 설정한 뒤 2 단계)로 넘어간다.
(2) 가설 검정
인자의 수가 적절한지 통계적으로 검정하는 방법이 있다. 먼저 귀무가설과 대립 가설은 다음과 같다.
$$ H_0 : \rho = LL^t + \psi, \;\; H_a : \text{not} H_0 $$
검정 통계량 $T$은 다음과 같다.
$$T = \{ n-1-(2p+4m+5)/6 \}\log \frac{|\hat{L}\hat{L}^t +\hat{\psi} |}{|R|}$$
여기서 $\hat{L}, \hat{\psi}$는 각각 $L, \psi$의 최대 우도 추정량이다.
이때 귀무가설이 참일 때 $T$는 점근적으로 자유도가 $\nu = ((p-m)^2-p-m)/2$인 $\chi^2$ 분포에 근사한다. 이때 자유도는 양수이기 때문에 다음을 만족해야 한다.
$$ m < \frac{1}{2}(2p+1-\sqrt{8p+1}) $$
유의 수준 $\alpha$에 대해서 $T>\chi^2(\alpha; \nu)$이면 귀무가설을 기각하고 공통 인자 수를 기존 보다 더많이 확보해야한다는 것을 암시하며 $T\leq \chi^2(\alpha; \nu)$라면 귀무 가설을 채택하고 공통 인자 수가 적절하다는 판단을 하게 된다.
3) 인자의 회전
인자 적재 행렬을 추정했다고 하더라도 회전을 통해 더 해석력이 좋은 인자 적재 행렬을 얻을 수 있다. 회전의 필요성을 알아보기 위해 아래 그림과 같이 3가지 인자 적재 행렬이 추정되었다고 해보자. 위 테이블은 공통 인자가 2개인 경우 인자 적재를 나타낸 것이며 아래 그림은 F1을 x축, F2를 y축으로 했을 때 산점도를 나타낸 것이다.
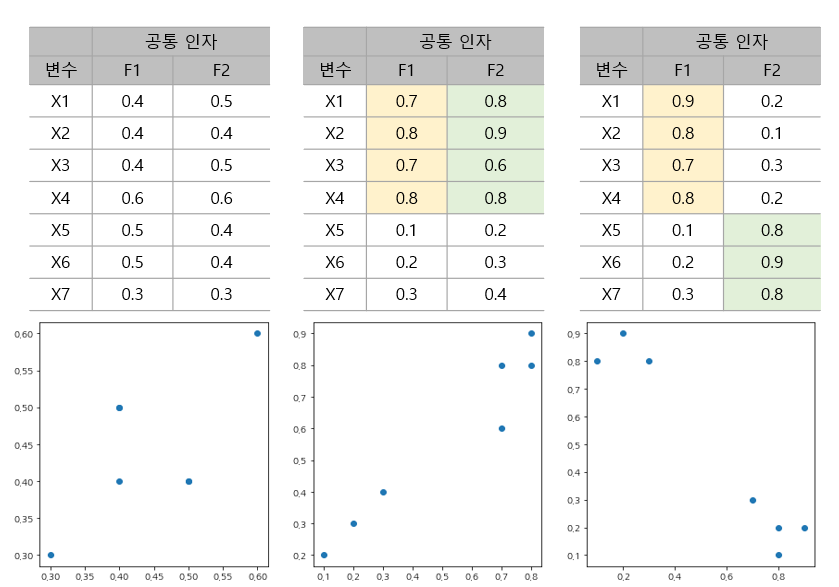
가장 왼쪽에 있는 결과가 제일 해석하기 난해한 인자 적재 행렬이다. 이 경우는 변수 7개를 2개의 공통인자로 설명하는 차원 축소 효과 말고는 좋은 점이 없다. 해석력이 있으려면 공통 인자가 특정 변수의 가중치가 크고 나머지 변수에는 낮은 구조가 되어야 한다. 하지만 그게 다가 아니다. 이를 중간에 있는 인자 적재 행렬이 보여준다. 이 경우 각 공통 인자는 X1~X4에 가중치가 높고 나머지는 가중치가 낮은 것을 알 수 있다. 물론 왼쪽 인자 적재 행렬보다는 해석력이 있지만 이 경우 공통 인자 2개 모두 같은 역할을 하고 있으므로 굳이 2개를 사용할 이유가 없다. 마지막으로 오른쪽 인자 적재 행렬이 가장 이상적인 구조로써 첫 번째 공통 인자는 X1~X4의 상관 구조를 설명하고 두 번째 공통 인자는 X5~X7의 상관 구조를 설명하고 있다. 즉, 각 공통 인자들이 배타적으로 다른 말로 말하면 가장 효율적으로 변수들의 상관 구조를 설명하고 있는 것이다. 즉, 각 공통 인자들이 배타적으로 특정 변수에 대하여 가중치가 높고 나머지 변수들에는 가중치가 낮은 구조를 갖는 인자 적재 행렬이 해석력이 가장 좋은 것이다.
시각적으로 살펴보면 해석력이 가장 좋은 경우 위에서 우측 하단의 산점도와 같이 데이터들이 공통 인자 어느 한 축에 쏠려 있으면서 그 축에 대해서 0에서 최대한 멀리 떨어져 있어야 한다.
인자 회전 방법은 크게 직교 회전(Orthogonal Rotation)과 사각 회전(Oblique Rotation)이 있다. 직교 회전은 축끼리 수직을 유지하여 바꾸는 방법이고 사각 회전은 축의 수직은 포기하는 대신 해석력에 포커스를 맞춘 회전 방법이다. 아래 그림은 직교 회전과 사각 회전을 나타낸 것이다.

사각 회전은 직교 회전과는 달리 공통 인자에서 인자 적재 간 상관성을 재 해석해야 하는 과정이 추가되고 그 해석이 어렵기 때문에 사각 회전보다는 직교 회전이 선호된다.
이제 직교 회전과 사각 회전에 몇 가지 종류를 알아보자.
a. 직교 회전(Orthogonal Rotation)의 종류
앞에서 해석력이 좋은 인자 적재 행렬은 인자 적재 값이 한 축에 쏠려있으면서 0에서는 멀리 떨어져 있어야 한다고 했었다. 인자 적재 값들이 열 방향 또는 행 방향으로 분포가 작은 값과 큰 값으로 분리되어 있는 것이 좋다는 것이며 수학적으로는 분산과 관련이 있는 것이다.
본격적으로 시작하기에 앞서 인자 적재 행렬 $L$을 직교 행렬 $R$에 의하여 변환된 것을 $L^*$라 하자. 즉,
$$L^* = LR$$
이다. 또한 $L^*_{ij} = l^*_{ij}$이다. 이때
$$L^*(L^*)^t = (LR)(LR)^t = L(RR^t)L^t = LL^t$$
이므로 $LL^t$의 대각 원소인 공통성은 직교 회전에 대해서 불변하다는 것을 알 수 있다. 즉,
$$\sum_{j=1}^m(l_{ij}^*)^2 = \text{Const. w.r.t Orthogonal Rotation} \;\; \forall i=1, \ldots, p$$
(1) Quartimax 회전
Quartimax 회전은 인자 적재 행렬에서 행 방향 인자 적재 제곱의 분산을 최대화하는 회전을 의미한다. Quartimax는 Carroll, Neuhaus와 Wrigley, Saunders, 그리고 Ferguson이 각기 다른 목적함수를 최소 또는 최대화하는 방식으로 제안했다. 하지만 이들의 목적함수는 직교 회전이라는 제약이 추가되면 모두 동일하므로 여기서는 Ferguson이 제시한 목적함수를 소개한다. Quartimax 회전은 다음과 같이 인자 적재의 4 승합을 최대화하는 직교 행렬을 찾는다.
$$ \sum_{i=1}^p \sum_{j=1}^m (l^*_{ij})^4 \tag{24} $$
Quartimax에서 'Quati'는 (24)의 4승을 의미한다. (24)를 최대화하는 것이 행 방향 인자 적재 제곱의 분산을 최대화하는 것과 어떤 연관이 있는지 살펴보자.
일단 $i$번째 행의 인자 적재 행렬 제곱의 분산 $q_i$를 생각해 보자.
$$ q_i = \frac{1}{m} \sum_{j=1}^m (l^*_{ij})^4 - \left( \frac{1}{m} \sum_{j=1}^m (l^*_{ij})^2 \right )^2 $$
그리고 $q_i$를 모든 $i$에 대해서 더해주면
$$\begin{align}q &= \sum_{i=1}^pq_i \\ &= \sum_{i=1}^p \left \{ \frac{1}{m} \sum_{j=1}^m (l^*_{ij})^4 - \left( \frac{1}{m} \sum_{j=1}^m (l^*_{ij})^2 \right )^2 \right \} \end{align} \tag{25}$$
(25)를 최대화한다는 것이 바로 행 방향 인자 적재 제곱의 분산을 최대화하는 것이다. 이때 (25) 마지막 식에서 두 번째 항은 직교 변환에 대해서 불변이고 남는 항에서 앞에 곱해진 상수를 제외하면 (25)를 최대화하는 것과 (24)를 최대화하는 것과 같아지는 것이다.
(25)에서 두 번째 항은 인자 적재 자승의 평균이고 이것이 항상 불변하므로 인자 적재 자승의 제곱(즉, 4승)을 최대화 시키면 인자 적재 자승이 최대한 떨어질 수 있다는 것이 Quartimax의 아이디어인 것이다.
(2) Varimax 회전
Quartimax 회전이 인자 적재 행렬에서 행 방향 인자 적재 자승의 분산을 최대화하는 기준이라면 Varimax 회전은 인자 적재 행렬에서 열 방향 인자 적재 자승의 분산을 최대화하는 기준이다.
인자 적재 행렬의 $j$번째 열의 제곱의 분산 $v_j$를 생각해 보자.
$$ v_j = \frac{1}{p} \sum_{i=1}^p (l_{ij}^*)^4 - \left ( \frac{1}{p} \sum_{i=1}^p (l_{ij}^*)^2 \right )^2 $$
그리고 $v_j$를 모든 $j$에 대해서 더해주면
$$\begin{align} v &= \sum_{j=1}^m v_j \\ &= \sum_{j=1}^m \left \{ \frac{1}{p} \sum_{i=1}^p (l_{ij}^*)^4 - \left ( \frac{1}{p} \sum_{i=1}^p (l_{ij}^*)^2 \right )^2 \right \} \end{align} \tag{26}$$
Varimax는 (26)에서 $v$를 최대화하는 직교 행렬을 찾는 것이다. Varimax와 Quartimax는 서로 거의 유사해 보인다. 하지만 Varimax를 제안한 Kaiser는 (1) 인자 적재 행렬의 서로 다른 열끼리의 상관성을 최소화할 수 있다는 점에서 더 나은 해석을 할 수 있고 (2) 직교 회전의 검증 데이터라고 할 수 있는 Thurstone의 데이터를 이용하여 Varimax가 Quatimax 보다 더 해석력 좋은 인자 적재 행렬을 가진다는 것을 보였다.
Varimax와 Quartimax 회전을 찾는 최적화 문제에 관심이 생겨 찾아보다가 Jennrich가 제안한 알고리즘을 많이 쓰는 것 같아 소개한다. Varimax나 Quartimax를 일반적인 최적화 문제로 바꿔보자.
직교 행렬의 집합을 $\mathcal{M}$이라하고 최적화할 목적 함수를 $f$라 한다면 Varimax, Quartimax는 다음과 같은 최적화문제로 바꿀 수 있다.
$$\text{Maximize}\;\;\; f(R), R\in \mathcal{M} \tag{27} $$
Jennrich가 제안한 알고리즘은 다음과 같다.
알고리즘 3
1 단계) 오차 한계 $\epsilon>0$과 $\alpha \geq 0$과 초기 직교 행렬 $R^{(0)}$을 선택한다.
$l=1, 2, \ldots$에 대해서 2 단계)~ 4 단계)를 반복한다.
2 단계) $G = \left [ \frac{df}{dR} \right ]_{R=R^{(l-1)}}$을 계산한다.
3 단계) $ G+\alpha R^{(l-1)}$에 대하여 특이값 분해(SVD)를 수행한다. 즉,
$$USV^t = G+\alpha R^{(l-1)}$$
4 단계) $R^{(l)} = UV^t$로 설정한다. $|f(R^{(l)}) - f(R^{(l-1)}) | <\epsilon $이면 알고리즘을 종료하고 아니면
$R^{(l-1)} \longleftarrow R^{(l)}$로 설정한 뒤 2 단계)로 넘어간다.
4 단계)에서 $R=UV^t$은 $f$의 1차 근사 함수를 최대화하는 직교 행렬이라는 사실에 기인한 것이다. Jennrich는 이 알고리즘이 때때로 수렴하지 않을 수 있지만 $\alpha$ 값을 잘 정하면 초기값에 관계 없이 수렴한다는 것을 보였으며 Varimax와 Quartimax에 대해선 $\alpha = 0$을 쓰면 된다고 한다.
이제 (26)을 Varimax와 Quartimax 회전에 대한 목적함수까지 모두 포함하도록 다음과 같은 목적함수를 생각해 보자.
$$ f(R) = \sum_{j=1}^m \sum_{i=1}^p (l_{ij}^*)^4 - \frac{\gamma}{p} \sum_{j=1}^m \left ( \sum_{i=1}^p (l_{ij}^*)^2 \right )^2 \tag{27}$$
$l_{ij}^*$는 $R$의 함수이며 $\gamma=1$인 경우 Varimax, $\gamma=0$인 경우 Quartimax의 목적 함수가 된다.
(27)을 행렬로 표현해보자. $L^* = LR$이다.
$$\begin{align} f(R) &= \sum_{j=1}^m \sum_{i=1}^p (l_{ij}^*)^4 - \frac{\gamma}{p} \sum_{j=1}^m \left ( \sum_{i=1}^p (l_{ij}^*)^2 \right )^2 \\ &= \text{tr} ( (L^* \odot L^*)^t (L^* \odot L^*) ) - \frac{\gamma}{p} 1_p^t (L^* \odot L^*) (L^* \odot L^*)^t 1_p \\ &= \text{tr} \left \{ ((L^*)^t \odot (L^*)^t \odot (L^*)^t ) L^* \right \} - \frac{\gamma}{p} \text{tr}\left \{ L^* \text{diag} ((L^*)^t L^*) (L^*)^t \right \} \\ &= \text{tr} \left \{ R^t L^t (L^* \odot L^* \odot L^* ) \right \} - \frac{\gamma}{p} \text{tr}\left \{ (L^*)^tL^* \text{diag}((L^*)^tL^*) \right \} \\ &= \text{tr} \left \{ R^t L^t (L^* \odot L^* \odot L^* ) - \frac{\gamma}{p} R^tL^t L^* \text{diag}((L^*)^tL^*) \right \} \\ &= \text{tr}(R^t Q(R)) \end{align}$$
여기서
$$Q(R) = L^t (L^* \odot L^* \odot L^* ) - \frac{\gamma}{p} L^t L^* \text{diag}((L^*)^tL^*)$$
이제 $f(R) = \text{tr}(R^tQ)$라 해보자. 이때 $Q(R)$을 고정시키면 $df/dR = Q(R)$가 된다. 이때 $R^{(0)}=I$로 설정하며 종료 조건을 $f$값이 아닌 특이값 분해에서 나온 $S$의 대각 원소의 합 $\text{tr}(S)$을 사용하는 경우도 있는데 이러한 사실을 이용하여 Varimax(또는 Quartimax) 회전 행렬 $R$을 찾는 알고리즘은 다음과 같이 쓸 수 있다.
알고리즘 4
1 단계) 오차 한계 $\epsilon>0$과 $\alpha = 0$과 초기 직교 행렬 $R^{(0)} = I, d^{(0)} = 0$을 선택한다.
$l=1, 2, \ldots$에 대해서 2 단계)~ 4 단계)를 반복한다.
2 단계) $G = \left [ \frac{df}{dR} \right ]_{R=R^{(l-1)}} = Q(R^{(l-1)})$을 계산한다.
3 단계) $ Q(R^{(l-1)}) $에 대하여 특이값 분해(SVD)를 수행한다. 즉,
$$USV^t = Q(R^{(l-1)}) $$
4 단계) $R^{(l)} = UV^t, d^{(l)}=\text{tr}(S)$로 설정한다. $l\neq 1$이고 $ d^{(l)}/d^{(l-1)}< 1+\epsilon$이면 알고리즘을 종료하고 아니면
$R^{(l-1)} \longleftarrow R^{(l)}$로 설정한 뒤 2 단계)로 넘어간다.
b. 사각 회전(Oblique Rotation)의 종류
(1) Oblimin
앞에서 해석력이 좋은 인자 적재 행렬은 인자 적재 값이 한 축에 쏠려있어야 한다고 했다. 이는 인자 적재 행렬의 어느 한 칼럼이 다른 칼럼과는 수직 관계일 수록 좋은 것이며 이는 인자 적재 행렬의 각 칼럼들끼리의 상관성이 작아야 함을 의미한다.
정방 행렬 $R$에 대하여 $L^* = LR$이라 할 때 Oblimin은 인자 적재 행렬에서 칼럼에 대한 자승의 상관성을 최소화하는 $R$을 찾게 되며 목적 함수는 다음과 같다.
$$\sum_{j < k} \left \{ p \sum_{i=1}^p (l^*_{ij})^2(l^*_{ik})^2 -c \left ( \sum_{i=1}^p(l^*_{ij})^2 \right ) \left ( \sum_{i=1}^p (l^*_{ik})^2 \right ) \right \} $$
이때 $c$는 사전에 지정해줘야 하는 상수이며 $0\leq c \leq 1$을 주로 사용하는 것 같다.
(2) Promax
Promax는 인자 적재 행렬을 직교 회전한 후 인자 적재 값의 승수를 이용하여 작은 값을 더 작게 만들어 인자 적재 행렬의 칼럼 간 상관성을 낮추는 2 단계(Two-Stage) Oblique 방법이다.
Promax 방법은 다음과 같다.
1 단계) 직교 회전 방법(예 : Varimax 회전)을 이용하여 직교 행렬 $R$을 얻은 뒤 기존 인자 적재 행렬 $L$을 $R$에 의하여 회전시킨 인자 적재 행렬을 $L^*$라 하자. 즉, $L^* = LR$이다.
2 단계) $k>1$를 설정하고 $P$를 $L^*$를 이용하여 다음과 같이 만들어 준다.
$$p_{ij} = \text{sign}(l^*_{ij}) l^*_{ij} (l^*_{ij})^{k-1} $$
그런 다음 $R^* = \left \{ (L^*)^tL^* \right \}^{-1} (L^*)^t P$가 최종적인 Oblique 행렬이 되는 것이다. 이때 $R^*$의 칼럼 자승 합이 1이 되도록 정규화를 해준다. 최종 인자 적재 행렬은 $L' = L^*R^*$이다.
Promax의 아이디어는 인자 적재 행렬을 직교 회전한 뒤 인자 적재 행렬에서 칼럼 간 상관성을 낮추는 보정을 하는 것이다. 이때 (직교) 회전된 인자 적재 행렬 값을 부호는 유지하면서 승수를 취하는 방법으로 상관성을 낮추었다는 것이 Promax의 핵심이다. 이렇게 하면 절대값이 작은 값을 더 작게 만드는 효과가 있어 인자 적재 행렬 칼럼 간 상관성을 낮출 수 있는 것이다. 또 하나의 특징은 Oblique 행렬을 계산할 때 최소 제곱법을 쓴다는 것이다. 직교 회전된 인자 적재 행렬 $L^*$와 이를 보정한 $P$가 있을 때 $L^*$을 이용하여 $P$를 잘 근사할 수 있는 Oblique 행렬 $R^*$를 최소 제곱법으로 구하는 것이다.
4) 인자 점수 계산
인자 점수는 공통 인자 $f$의 추정치를 의미한다. 인자 분석의 주요 관심사는 인자 적재 행렬을 추정하는 것이지만 (1) 인자 공간에서 개별 관측치의 위치를 검토할 필요가 있고 (2) 인자 점수를 새로운 변수로 활용할 수 있기 때문에 인자 점수를 계산하는 것이 필요하다.
인자 점수는 관측되지 않은 잠재 변수이므로 계산 편의성을 위해 다음과 같은 사항을 따르게 된다.
1) 추정된 인자 적재 행렬 $\hat{L}$과 특정 분산 $\hat{\psi}$를 참값으로 간주한다.
2) 표준화된 변수 집단에 대하여 회전된 인자 적재의 추정치와 특정 분산의 추정치를 이용한다.
인자 점수를 추정하는 방법은 Bartlett이 제안한 가중 최소 제곱법과 Thomson이 제안한 회귀 방법이 있는데 어느 방법이 더 좋다고 할수는 없다고 한다. 각 방법에 대해서 알아보자.
a. 가중 최소 제곱법(Weighted Least Square Method)
모형 (2)에 대하여 $\mu, L, \psi$를 알고 있다고 할 때 Bartlett은 가중 오차 제곱합
$$\epsilon^t \psi^{-1} \epsilon = (X-\mu-Lf)^t \psi^{-1} (X-\mu-Lf) \tag{27} $$
을 최소화하는 방식으로 인자 점수 $f$를 추정하자고 제안하였다.
(27)을 최소화하는 $\hat{f}$는 다음과 같다.
$$ \hat{f} = (L^t\psi^{-1}L)^{-1} L^t\psi^{-1}(X-\mu)$$
위 식을 추정치로 바꾸면 $i$번째 변수에 대한 인자 점수는 다음과 같이 추정할 수 있다.
$$\hat{f}_j = (\hat{L}^t \hat{\psi}^{-1}\hat{L})^{-1} \hat{L}^t \hat{\psi}^{-1}(x_i-\bar{x}) \tag{28}$$
만약 $L$과 $\psi$를 최대 우도 추정량으로 추정했다면 $\hat{L}^t \hat{\psi}^{-1}\hat{L}$이 대각 행렬이므로 이를 $\hat{\Delta}$라 하면 (28)을 다음과 같이 쓸 수 있다.
$$\hat{f}_i = \hat{\Delta}^{-1} \hat{L}^t \hat{\psi}^{-1}(x_i-\bar{x}) \tag{29}$$
만약 주성분 방법으로 $L$과 $\psi$를 추정했다면 $\hat{\psi} = I$로 취급하여 인자 점수를 계산한다.
b. 회귀 방법(Regression Method)
회귀 방법은 $\epsilon$와 $f$의 결합 분포를 $m+p$차원 정규분포로 가정한다. 앞에서 다룬 모형에 대한 설정을 이용하면 $X-\mu$와 $f$의 결합 분포는 $N_{m+p}(0, \Sigma^*)$가 된다. 여기서
$$\Sigma^* = \begin{pmatrix} \Sigma_{p\times p} = LL^t+\psi & L_{p\times m} \\ L^t_{m\times p} & I_{m\times m} \end{pmatrix} \tag{30}$$
이때 $X=x$로 주어진 경우 $f$의 조건부 기대값을 계산하면 다음과 같다.
$$E(f|X=x) = L^t\Sigma^{-1} (x-\mu) = L^t(LL^t+\psi)^{-1}(x-\mu) \tag{30}$$
(30)에서 $f$의 조건부 기대값을 인자 점수로 추정하자는 것이 회귀 방법인 것이다. 따라서 $i$번째 변수에 대한 인자 점수는 다음과 같이 추정한다.
$$\hat{f}_i = \hat{L}^t(\hat{L}\hat{L}^t+\hat{\psi})^{-1}(x_i-\bar{x})\tag{31}$$
이때 $\hat{\Sigma}$을 $\hat{L}\hat{L}^t+\hat{\psi}$로 추정하는 대신 표본 공분산 행렬 $S$을 이용하여 인자 점수를 다음과 같이 추정할 수도 있다.
$$\hat{f}_i = \hat{L}^tS^{-1}(x_i-\bar{x})\tag{31}$$
이렇게 하면 $L$의 인자의 수를 제대로 설정하지 못해서 발생하는 에러 효과를 줄일 수 있다.
5) 인자 분석(Factor Analysis)의 절차
인자 분석은 (1) 인자 적재 행렬 추정, (2) 인자 적재 행렬 회전, (3) 인자 점수 계산 그리고 (4) 해석 단계로 이루어진다. 아래에서 인자 분석 절차대로 예제를 풀어본다.
3. 파이썬 구현
이번엔 인자 분석 과정을 파이썬으로 구현해보고자 한다. 아래 코드는 인자 분석을 수행하는 클래스 FactorAnalysis를 구현한 것이다. FactorAnalysis에서 fit 메서드는 주성분 방법을 통해 인자 적재 행렬을 추정하고 적절하게 회전시킨 뒤에 인자 점수를 추정한다.
class FactorAnalysis:
def __init__(self):
self.loadings = None ## 인자 적재 행렬
self.rotation_matrix = None ## 회전 행렬
self.rotated_loadings = None ## 회전시킨 인자 적재 행렬
self.factor_score = None ## 인자 점수
self.factor_score_coefficent = None ## 인자 점수 계수
self.cov_mat = None ## 표본 공분산 행렬
self.explained_variance = None ## 분산 설명 비율
def fit(self, X, num_factor=2, rotation_type='varimax', k=4, max_iter=1000, eps=1e-05):
assert rotation_type in ['varimax', 'promax']
self.get_loadings(X, num_factor) ## 인자 적재 행렬
L = self.loadings
## 인자 회전
self.get_rotated_loadings(L, rotation_type=rotation_type,
max_iter=max_iter, eps=eps, k=k)
self.get_factor_score(X)
return self
def get_rotated_loadings(self, L, rotation_type, k, max_iter, eps):
if rotation_type == 'varimax':
R, rotated_L = self._varimax(L, max_iter=max_iter, eps=eps)
self.rotation_matrix = R
self.rotated_loadings = rotated_L
else:
R, rotated_L = self._promax(L, k=k, max_iter=max_iter, eps=eps)
self.rotation_matrix = R
self.rotated_loadings = rotated_L
def _varimax(self, L, max_iter=1000, eps=1e-05): ## varimax 회전
R = np.eye(L.shape[1])
d_old = 0
p = L.shape[0]
for i in range(max_iter):
L_star = L @ R
Q = L.T @ (L_star ** 3 - (L_star @ np.diag(np.diag(L_star.T @ L_star)))/p)
U, S, V_t = np.linalg.svd(Q)
R = U @ V_t
d_new = np.sum(S)
if d_new < d_old * (1 + eps):
break
else:
d_old = d_new
return R, L_star
def _promax(self, L, k=4, max_iter=1000, eps=1e-5): ## promax
_, L_star = self._varimax(L, max_iter=max_iter, eps=eps)
P = L_star * (np.abs(L_star) ** (k-1))
L_inv = np.linalg.inv(L_star.T @ L_star)
R = L_inv @ L_star.T @ P
R = R/np.sqrt(np.sum(np.square(R), axis=0))
L_final = L_star @ R
return R, L_final
def get_loadings(self, X, num_factor): ## 인자 적재 행렬
cov_mat = (X - np.mean(X, axis=0)).T @ (X - np.mean(X, axis=0))/(X.shape[0]-1)
self.cov_mat = cov_mat
eigen_value, eigen_vector = np.linalg.eig(cov_mat)
eigen_value = eigen_value[:num_factor]
eigen_vector = eigen_vector[:, :num_factor]
loadings = np.sqrt(eigen_value)*eigen_vector
self.loadings = loadings
self.explained_variance = np.sum(eigen_value)/X.shape[1]
def get_factor_score(self, X):
L = self.rotated_loadings
S_inv = np.linalg.inv(self.cov_mat)
factor_score = L.T @ S_inv @ (X-np.mean(X, axis=0)).T
self.factor_score_coefficent = (L.T @ S_inv).T
self.factor_score = factor_score.T4. 예제
앞에서 구현한 인자 분석 코드를 확인해 볼 시간이다. 실제 데이터를 통하여 인자 분석을 수행해 본다. 여기서는 스위스의 47개 프랑스어권 지방에 대한 데이터이며 땅의 비옥도와 사회 경제적 지표 변수를 포함한다. 구체적인 변수 설명은 다음과 같다.
Province : 지방 이름
Fertility : 땅의 비옥도
Agriculture : 남성의 농업 종사율
Examination : 군 시험에서 최고 점수를 받은 징집병 비율
Education : 초등학교 보다 높은 교육을 받은 징집병 비율
Catholic : 가톨릭 비율
Infant.Mortality : 생후 1년 미만의 유아 사망률
데이터는 아래에 첨부해 두었으니 다운받으면 된다.
이제 데이터를 불러온 뒤 표준화를 먼저 수행한다.
import numpy as np
import pandas as pd
df = pd.read_excel('./swiss.xlsx')
X = df.drop('Province', axis=1).values
X = (X - np.mean(X, axis=0))/np.std(X, axis=0, ddof=True) ## 표준화
그리고 인자 분석을 수행한다. 이때 공통 인자 개수는 시각화를 위하여 2개로 설정했다.
fa = FactorAnalysis().fit(X, num_factor=2, rotation_type='promax')
이제 결과를 하나씩 살펴보자.
1) 인자 적재 행렬 추정
## 인자 적재 행렬
loadings = pd.DataFrame(fa.loadings,
index=df.columns[1:],
columns=[f'Factor_{i+1}' for i in range(fa.loadings.shape[1])])
loadings
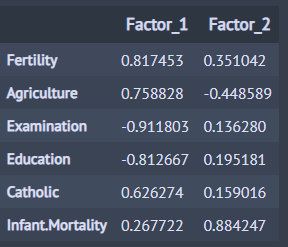
인자 적재 값들이 뭔가 명확하지 않은 것 같다. 특히 첫 번째 공통 인자(Factor_1)는 유아 사망률을 제외하면 인자 적재 값이 모두 0.6 이상으로 꽤나 크다. 이렇게 하나의 공통 인자에 인자 적재 값이 많이 크면 공통 인자의 의미를 해석하기가 어려울 수 있다. 시각화도 해보았다. 이때 나중에 회전된 결과와 비교하기 위하여 검은색 선으로 축을 표시했다.
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False
fig = plt.figure(figsize=(6,6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.plot([0, 1], [0, 0], color='k')
ax.plot([0, 0], [0, 1], color='k')
ax.scatter(loadings['Factor_1'], loadings['Factor_2'])
plt.show()

흠.. 잘 모르겠다. 그렇다면 회전된 인자 적재 행렬은 얼마나 해석력이 좋은지 살펴보자.
2) 인자 회전
이번엔 Promax 방법을 이용하여 인자 적재 행렬을 회전시킨 결과를 살펴보자.
rotated_loadings = pd.DataFrame(fa.rotated_loadings,
index=df.columns[1:],
columns=[f'Factor_{i+1}' for i in range(fa.rotated_loadings.shape[1])])
rotated_loadings
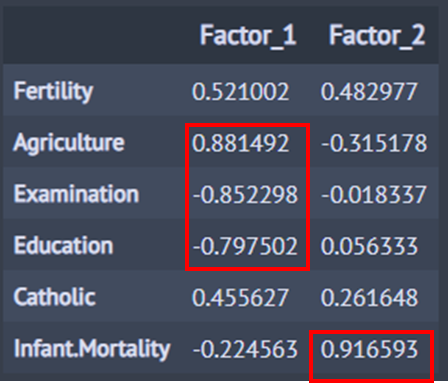
아까 보단 좀 더 명확해진 것 같다. 위에 빨간 네모는 절대값이 0.7보다 큰 인자 적재를 나타낸 것이다. 첫 번째 공통 인자(Factor_1)는 (징집병 대부분이 남성이라는 가정하에) 남성의 지능과 관련된 인자이고 두 번째 공통 인자는 유아 사망률과 관련된 인자라고 해석할 수 있다. 인자 회전을 할 때 유의해야 할 점은 인자 회전을 통해 해석력 좋은 인자 적재 행렬을 항상 얻을 수 있는 것이 아니며 해석력 좋은 인자 적재 행렬을 만들 수 있는 가능성이 있다는 것이다.
이번엔 회전이 어떻게 진행되었는지 살펴보기 위하여 기존 인자 적재 행렬에 회전된 축을 빨간 선으로 표시하였다.
rotation_matrix = fa.rotation_matrix
fig = plt.figure(figsize=(6,6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(loadings['Factor_1'], loadings['Factor_2'])
ax.plot([0, 1], [0, 0], color='k')
ax.plot([0, 0], [0, 1], color='k')
ax.plot([0, rotation_matrix[0, 0]], [0, rotation_matrix[1, 0]], color='r')
ax.plot([0, rotation_matrix[0, 1]], [0, rotation_matrix[1, 1]], color='r')
plt.show()
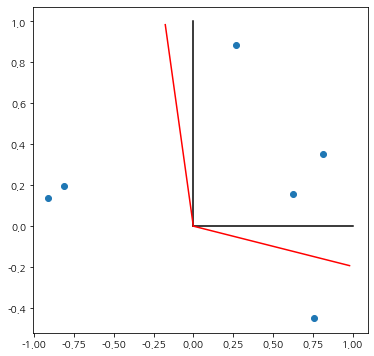
직교 회전이 아니므로 위와 같은 결과는 지극히 정상적이다.
3) 인자 점수 계산
먼저 인자 점수 계수$(\hat {L}^tS^{-1})^t$를 계산해 보자.
## 인자 점수 계수
score_coefficent = pd.DataFrame(fa.factor_score_coefficent,
index=df.columns[1:],
columns=[f'Factor_{i+1}' for i in range(fa.rotated_loadings.shape[1])]
)
score_coefficent

위 결과를 수식으로 쓰면 다음과 같다.
$$\begin{align} \hat{f}_1 &= 0.067 \cdot \text{Fertility}+0.397\cdot\text{Agriculture} -0.303\cdot \text{Examination} \\ & -0.302 \cdot \text{Education} + 0.099 \cdot \text{Catholic} -0.310 \cdot \text{IM} \\ \hat{f}_2 &= 0.334 \cdot \text{Fertility}-0.332\cdot\text{Agriculture}+ 0.065 \cdot \text{Examination} \\ & + 0.119 \cdot \text{Education} + 0.165 \cdot \text{Catholic} +0.747 \cdot \text{IM} \end{align} \tag{32}$$
첫 번재 인자 점수는 남성의 농업 종사율이 높거나 군 시헌에서 최고 점수를 받거나 초등학교 보다 높은 수준의 교육을 받은 징집병의 비율이 낮을수록 커진다. 두 번째 인자 점수는 생후 1년 미만의 유아 사망률이 크면 큰 값을 가진다.
이번엔 지방별 인자 점수를 계산하여 시각화를 해보았다.
## 인자 점수 계산
factor_score = pd.DataFrame(fa.factor_score, index=df['Province'],
columns=[f'Factor_{i+1}' for i in range(fa.rotated_loadings.shape[1])])
rotation_matrix = fa.rotation_matrix
fig = plt.figure(figsize=(6,6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(factor_score['Factor_1'], factor_score['Factor_2'])
ax.set_xlabel('Factor_1')
ax.set_ylabel('Factor_2')
plt.show()

첫 번째 인자 점수와 두 번째 인자 점수 사이의 음의 상관성을 보인다. 인자 점수 산점도는 그 자체로는 큰 의미가 없을 수 있지만 특정 범주(소득 수준이 높음 또는 낮음)에 대하여 다른 색상으로 표시했을 때 색상별로 분포가 어떤지 확인하여 의미 있는 해석을 할 수도 있다. 예를 들어 위 데이터에서 소득 수준이 높은 지방과 낮은 지방의 범주가 있고 이를 색상으로 표시했다고 하자(소득 수준이 높으면 파랑, 낮으면 빨강).
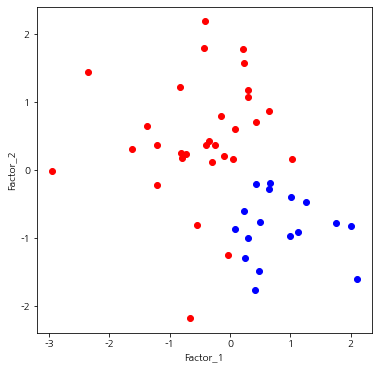
이 경우 첫 번째 인자 점수가 높거나 두 번째 인자 점수가 낮으면 소득 수준이 높은 지역이라는 해석을 할 수 있고 새로운 데이터가 들어왔을 때 (32)를 이용하여 인자 점수를 계산하고 산점도에서 어느 위치에 있는지를 확인한 뒤 그 데이터가 소득이 높은 지역인지 아닌지 미리 예측해 볼 수 있을 것이다.
5. 장단점
인자 분석의 장단점은 다음과 같다.
- 장점 -
a. 크고 복잡한 데이터를 소수의 공통 인자를 이용하여 상관 구조를 찾아낼 수 있다.
b. 비슷한 변수들을 클러스터링할 수도 있다.
c. 해석력 높은 공통 인자를 추출하여 많은 변수들을 한 번에 설명할 수 있는 지표를 만들 수도 있다.
- 단점 -
a. 신뢰성 있는 추정 결과를 제공하기 위해 많은 샘플이 필요하다.
b. 공통 인자를 추정하는 방법과 인자 회전에 따라 결과가 크게 달라질 수 있다.
c. 인자 분석은 보통 공통 인자들 사이의 상관성이 없다고 가정하지만 실제로는 그렇지 않다.
d. 인자의 회전을 통해서도 인자 적재 행렬이 해석력이 좋은 구조가 안될 수 있으며 된다 하더라도 인자 적재 행렬 값 그 자체의 의미를 부여하기가 쉽지 않다.
- 참고 자료 -
R.J. Jennrich - A Simple General Procedure for Orthogonal Rotation
K.G. Joreskog - Some Contributions to Maximum Likelihood Factor Analysis
R.A. Johnson, D. W. Wichern - Applied Multivariate Statistical Analysis
H.F. Kasier - The Varimax Criterion for Analytic Rotation in Factor Analysis
성웅현 - 응용 다변량 분석





댓글