이번 포스팅에서는 밀도 기반 이상치 여부를 판단하는 지표인 Local Outlier Factor(LOF)에 대한 개념과 파이썬으로 구현해 보는 방법에 대해서 알아보고자 한다.
- 목차 -
1. Local Outlier Factor란?
1) 정의
Local Outlier Factor(LOF)는 주어진 데이터가 이상치라면 해당 데이터의 밀도가 주변 이웃의 밀도보다 작을 것이라는 아이디어에 착안하여 만들어진 밀도 기반 이상치 탐지 지표이다.
2) 파헤치기
Local Outlier Factor(LOF)에 대하여 하나씩 살펴보자. LOF의 수학적 정의를 위해 필요한 사전 정의들을 먼저 알아보고 그에 대한 의미를 하나씩 알아보도록 한다.
정의 1 $k$ 거리
데이터의 집합을 $D$라 할 때 양의 정수 $k$에 대하여 $x\in D$의 $k$ 거리 $d_k(x)$는 다음과 같이 정의한다.
$$d_k(x) = d(x, y),\;\; y\in D_x \;\;\text{such that} \\ \text{#}\{ y' \in D_x : d(x, y') \leq d(x, y) \} \geq k \\ \text{#}\{ y' \in D_x : d(x, y') < d(x, y) \} \leq k-1 \tag{1}$$
여기서 $d$는 거리 측도(예: Euclidean Distance), $D_x = D-\{x\}$이고 $\text{#}(A)$는 $A$의 원소 개수를 의미한다.
이번엔 또 다른 거리를 소개한다.
정의 1-1
$x$의 $k$ 이웃 거리는 $d_k'(x)$는 $x$와 가장 가까운 점들을 순서대로 나열한 것을 $y_1, y_2, \ldots $이라 할 때 동점을 포함하는 $k$번째로 가까운 거리 $d(x, y_k)$를 의미한다. 이때 $y_i$는 모두 다르며 $x\neq y_i, =1, 2, \ldots$이다.
사실 정의 1과 정의 1-1은 동치이다. 즉, 자연수 $k$에 대해서
$$d_k(x) = d_k'(x) \tag{1-1}$$
정의 1-1 $\Rightarrow$ 정의 1
$d_k'(x) = d(x, y_k)$이면 $d(x, y_1) \leq d(x, y_2) \leq \cdots \leq d(x, y_k)$이므로
$$\text{#}\{ y' \in D_x : d(x, y') \leq d(x, y_k) \} = k$$
이므로 $k$ 거리의 첫 번째 조건을 만족한다.
만약 $d(x, y_{k-1}) < d(x, y_k)$이면
$$\text{#}\{ y' \in D_x : d(x, y') < d(x, y_k) \} = k-1$$
이고 $d(x, y_{k-1}) = d(x, y_k)$이면
$$\text{#}\{ y' \in D_x : d(x, y') < d(x, y_k) \} \leq k-2$$
이므로 어느 경우든
$$\text{#}\{ y' \in D_x : d(x, y') < d(x, y_k) \} \leq k-1 $$
이 된다. 즉, $k$ 거리의 두 번째 조건을 만족하므로 $d_k'(x) $
정의 1 $\Rightarrow$ 정의 1-1
먼저 $x$와 $y \in D, y\neq x$의 거리를 계산한 뒤 오름차순으로 $k$까지만 정렬한 것을 $d(x, y_1) \leq d(x, y_2) \leq \cdots \leq d(x, y_k)$이라 하자. 그렇다면 우리는 다음을 보일 것이다.
$$d_k(x) = d(x, y_k) \tag{*}$$
먼저 $y_k$는 $k$ 거리의 첫 번째 조건을 만족한다. 만약 두 번째 조건을 만족하지 않는다고 해보자. 즉,
$$\text{#}\{ y' \in D_x : d(x, y') < d(x, y_k) \} \geq k \tag{**}$$
이다. 이때 $y_k$의 정의에 따라서 $d(x, y_{k-1}) \leq d(x, y_k)$이다.
만약 $d(x, y_{k-1}) < d(x, y_k)$라면
$$\text{#}\{ y' \in D_x : d(x, y') < d(x, y_k) \} = k-1$$
이고 $d(x, y_{k-1}) = d(x, y_k)$라면
$$\text{#}\{ y' \in D_x : d(x, y') < d(x, y_k) \} \leq k-2$$
이므로 어느 경우든 (**)를 만족하지 않게 된다. 이는 $d_k(x) = d(x, y_k)$가 위배되므로 $y_k$는 $k$ 거리의 두 번째 조건까지 만족하게 되는 것이다.
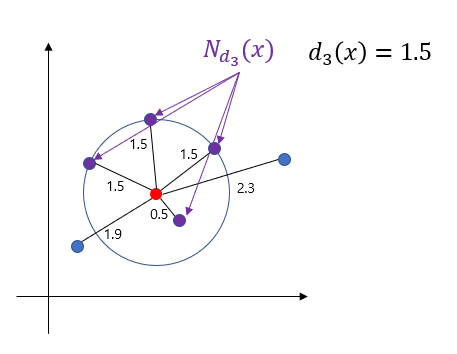
정의 1-1을 소개하는 이유는 기존 $k$ 거리가 복잡해 보이지만 정의 1-1을 이용하면 단순하게 계산할 수 있기 때문이다. $x$의 $k$ 거리는 $x$와 다른 데이터의 거리를 오름차순으로 정렬한 뒤 $k$ 번째 거리값을 취한 것이다. 아래 그림은 빨간 점($x$)에 대한 $3$ 거리인 $d_3(x)$를 계산하는 과정을 구한 것이다.

이번엔 $k$ 거리를 이용한 이웃(Neighborhood)를 정의한다.
정의 2 $k$ 거리 기반 이웃
주어진 데이터 $x \in D$에 대하여 $k$ 거리 기반 이웃 $N_{d_k}(x)$는 다음과 같이 정의한다.
$$N_{d_k}(x) = \{ y \in D_x : d(x, y) \leq d_k(x) \} \tag{2}$$
$k$ 거리 기반 이웃은 어려운 게 없다. 아래 그림은 $N_{d_3}(x)$(보라색 점)을 나타낸 것이다.
정의 3 $k$ 도달 가능 거리(Reachability Distance)
$x, y \in D$에 대하여 $x$의 $y$에 대한 $k$ 도달 가능 거리 $rd_k(x, y)$은 다음과 같이 정의한다.
$$rd_k(x, y) = \max \{ d_k(y), d(x, y) \} \tag{3}$$
아래 그림은 $3$ 도달 가능 거리를 나타낸 것이다.

$k$ 도달 가능 거리는 일반적인 거리와 다르게 교환 법칙이 성립하지 않는다.
$$rd_k(x, y) \neq rd_k(y, x)$$
이러한 사실은 아래 그림을 통해 알 수 있다.
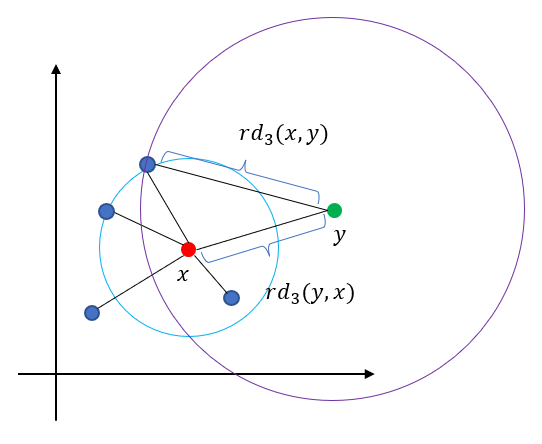
$k$ 도달 가능거리에서 max 연산은 큰 거리에 대해서는 큰 값을 주는 반면 가까운 거리에 대해서는 그 값을 너무 작게 주지 않게 한다. 이는 다음에 소개할 $k$ 지역 도달 가능 밀도를 작은 값에 민감하게 변하지 않도록 해주는 장치이다.
정의 4 $k$ 지역 도달 가능 밀도(Local Reachability Density)
주어진 데이터 $x \in D$의 $k$ 지역 도달 가능 밀도 $lrd_k(x)$는 다음과 같이 정의한다.
$$ lrd_k(x) = \left \{ \frac{ \sum_{y\in N_{d_k}(x) } rd_k(x, y)}{|N_{d_k}(x)|} \right \}^{-1} \tag{4}$$
$k$ 지역 도달 가능 밀도는 주어진 점이 밀도가 높은 곳에 있는지 낮은 곳에 있는지를 정량화한 수치이다.
아래 그림은 밀도가 높은 곳에 포함된 점(까만 점)과 낮은 곳에 포함된 점을 나타낸 것이다. 5 거리 기반 이웃을 파란색으로 표현하였다. 일반적으로 주어진 점이 높은 밀도에 속해있다면 이웃(파란 점) 간 평균 거리가 작을(가까울) 것이고(왼쪽) 낮은 밀도에 속해있다면 이웃 간 평균 거리가 클(멀) 것이다.

이는 주어진 점과 이웃인 평균 거리의 역수를 밀도 개념으로 사용할 수 있는 것이다. 이때 거리의 측도를 $k$ 도달 가능 거리로 사용한 것이 바로 $k$ 도달 가능 밀도인 것이다. 따라서 주어진 $k$에 대하여
$$lrd_k(x_1) < lrd_k(x_2)$$
이라면 $x_2$ 주변의 밀도가 크다고 해석할 수 있다.
정의 5 $k$ Local Outlier Factor
$x\in D$의 $k$ Local Outlier Factor $lof_k(x)$는 다음과 같이 정의한다.
$$\begin{align} lof_k(x) &= \frac{1}{|N_{d_k}(x)|} \sum_{y \in N_{d_k}(x)} \frac{lrd_k(y)}{lrd_k(x)} \\ &= \frac{\frac{1}{|N_{d_k}(x)|}\sum_{y \in N_{d_k}(x)} lrd_k(y)}{lrd_k(x)} \end{align} \tag{5}$$
$lof_k(x)$의 정의를 보면 분모는 주어진 점 $x$의 $k$ 지역 도달 가능 밀도이고 분자는 $x$ 이웃의 $k$ 지역 도달 가능 밀도이다. 따라서 주어진 점의 $k$ Local Outlier Factor(LOF)는 해당 점의 밀도가 이웃의 평균 밀도보다 얼마나 높은지 또는 낮은 지를 정량화한 것이라고 할 수 있다.
이때
$$\bar{lrd_k(y)} = \frac{1}{|N_{d_k}(x)|} \sum_{y \in N_{d_k}(x)}lrd_k(y)$$
라 하자. 아래 그림은 세 가지 경우에 대한 $k$ LOF 값을 비교한 것이다.

첫 번째 경우는 $x$의 밀도($k$ 도달 가능 밀도)가 높고 주변 이웃의 평균 밀도 또한 높다. 따라서 LOF의 분모 분자가 모두 크므로(모두 비슷한 값일 테니까) 이에 대한 $lof_k(x)$는 1에 가까울 것이다. 세 번째 경우는 $x$의 밀도와 주변 이웃의 평균 밀도가 모두 작은 경우이다. 이 경우도 첫 번째 경우와 마찬가지로 $lof_k(x)$는 1에 가까울 것이다. 두 번째 경우는 $x$의 밀도는 작고 주변 이웃의 평균 밀도가 큰 경우이다. 따라서 LOF의 분모는 작고 분자는 크므로 이에 대한 $lof_k(x)$는 1보다 많이 클 것이다. 이를 통해 LOF 값이 클수록 이상치일 가능성이 높아지는 것을 알 수 있다.
주어진 점의 밀도가 주변 이웃의 평균 밀도보다 작으면 이상치일 것이라는 아이디어에 착안한 것이 LOF이며 밀도를 사용했다는 점에서 LOF는 밀도 기반 이상치 탐지 지표(Density-Based Anamoly Detection Index)인 것이다.
2. 파이썬 구현
이제 LOF를 파이썬으로 구현해 보자. 아래 코드에서 LocalOutlierFactor 클래스는 $k$를 초기값으로 하고 fit 메서드를 이용하여 주어진 데이터의 LOF 값을 score 속성에 저장한다.
import numpy as np
class LocalOutlierFactor:
def __init__(self, k):
self.k = k
self.score = None
def distance(self, x, y): ## 거리 함수
return np.linalg.norm(x-y)
def get_k_distance_neighbor(self, x, X, k): ## k 거리 기반 이웃과 k 거리
drop_idx = np.where(np.sum(X == x, axis=1)==2)[0]
distance = np.array([self.distance(x, y) for y in X])
k_neighbor_idx = np.argsort(distance)[len(drop_idx):(k+len(drop_idx))]
return k_neighbor_idx, np.sort(distance)[k+len(drop_idx)-1]
def get_rd(self, x, y, k): ## k 도달 가능 거리
dist_xy = self.distance(x, y)
_, k_dist_y = self.get_k_distance_neighbor(y, X, k)
return np.max([dist_xy, k_dist_y])
def get_lrd(self, x, X, k): ## k 지역 도달 가능 밀도
k_neighbor, _ = self.get_k_distance_neighbor(x, X, k)
mean_rd = np.mean([self.get_rd(x, y, k) for y in X[k_neighbor, ]])
return 1/mean_rd
def get_lof(self, x, X, k): ## k lof
k_neighbor, _ = self.get_k_distance_neighbor(x, X, k)
lrd_x = self.get_lrd(x, X, k)
mean_lrd = np.mean([self.get_lrd(y, X, k) for y in X[k_neighbor]])
return mean_lrd/lrd_x
def fit(self, X):
k = self.k
result = np.array([self.get_lof(y, X, k) for y in X])
self.score = result
return self3. 예제
여기에서는 시뮬레이션 데이터를 이용하여 앞에서 구현한 LocalOutlierFactor를 테스트해 보자. 먼저 데이터를 만들어준다.
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False
np.random.seed(100)
x1 = 0.3 * np.random.randn(100, 2)
x2 = 3 * np.random.rand(30, 2)
X = np.r_[x1, x2]
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(X[:, 0], X[:, 1], color='k', s=10)
plt.show()
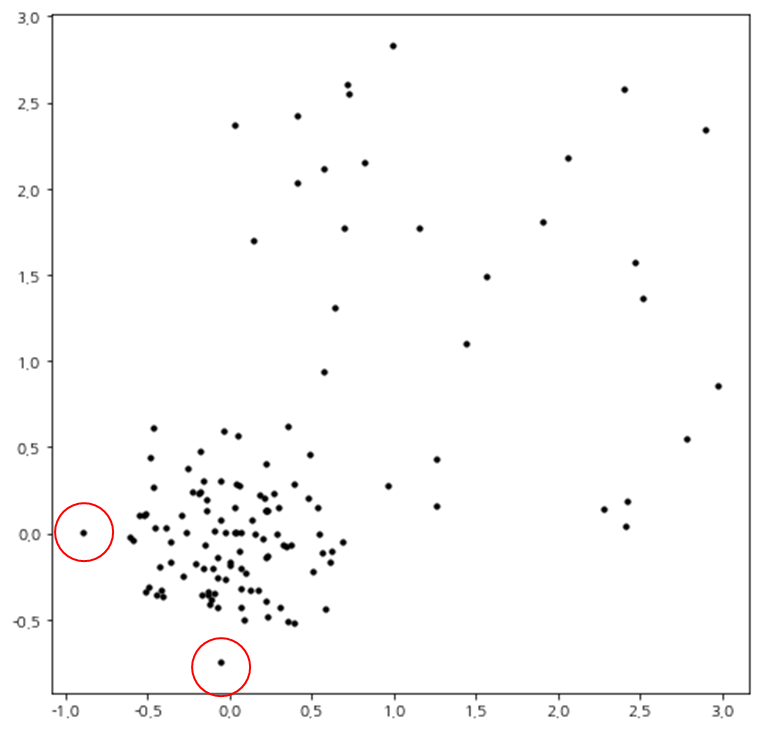
코드를 실행하면 산점도가 위와 같이 나오는데 밀도를 고려하면 빨갛게 표시된 부분이 이상치라 할 수 있으며 LOF는 이 2개의 점에 대하여 높은 값을 가져야 할 것이다.
이제 LocalOutlierFactor를 테스트해 보자. 여기서는 $k=5$로 설정했다.
lof = LocalOutlierFactor(k=5).fit(X)
이제 구해진 LOF 값을 이용하여 각 점에 대한 점수를 빨간 원으로 시각화해 보았다. 이때 원의 반지름은 LOF에 비례하도록 설정했다.
score = lof.score
radius = (score - np.min(score)) / (np.max(score) - np.min(score))
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(X[:, 0], X[:, 1], color='k', s=10, label='Data')
plt.scatter(X[:, 0], X[:, 1], s=1000 * radius, edgecolors='r',
facecolors='none', label='LOF score')
legend = plt.legend(loc='upper left')
legend.legendHandles[0]._sizes = [10]
legend.legendHandles[1]._sizes = [20]
plt.show()
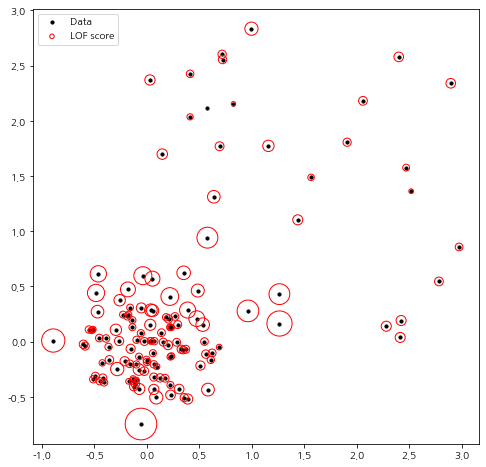
예상한 대로 이상치로 잡아야 할 점에 대해서 높은 LOF 값을 갖는 것을 확인했다. 다른 점에 대해서도 주변 밀도를 고려했을 때 합리적인 결과가 나온 것을 알 수 있다.
4. 장단점
LOF는 다음과 같은 장단점을 갖고 있다.
- 장점 -
a. 특별한 데이터의 분포를 가정하지 않고 사용할 수 있다.
b. 연속형 뿐만 아니라 범주형 데이터에 대해서도 거리만 잘 정의되어 있으면 적용할 수 있다.
c. 다양한 타입의 이상치를 잡아낼 수 있다.
LOF는 단순히 거리 기반이 아닌 밀도 기반 이상치 탐지 여부를 알아낼 수 있는 지표로써 기존에는 잡아내지 못했던 다양한 시나리오에 대해서 이상치를 잡아낼 수 있다.
d. 주어진 데이터에 대해서 이상치 정도를 비교할 수 있다.
- 단점 -
a. $k$와 거리 측도에 따라서 민감하다.
따라서 원하는 결과를 얻기 위해 $k$와 거리 측도에 대한 여러 조합에 대해서 실험을 필요로 한다.
b. 계산량이 상당히 많다.
c. LOF는 정상 데이터들의 밀도가 일정치 않다면 이상치를 정확하게 판별해내지 못할 수 있다.
d. LOF의 비교가 한정적이다.
LOF는 한 데이터 집합 내에서는 각 데이터 간 상대적 비교가 가능하다. 하지만 서로 다른 데이터 집합 간 비교가 불가능하다. 즉, 한 데이터 집합의 어떤 LOF 값과 다른 데이터 집합의 어떤 LOF의 비교가 불가능하다.
- 참고 자료 -
M. M, Breunig 외 3명 - LOF : Indentifying Density-Based Local Outliers
강필성 - 03-4: Anomaly Detection - Local Outlier Factor (LOF) (이상치 탐지 - LOF)
'통계 > 머신러닝' 카테고리의 다른 글
| 44. Isolation Forest에 대해서 알아보자. (0) | 2023.05.20 |
|---|---|
| 43. Support Vector Data Description(SVDD)에 대해서 알아보자 with Python (4) | 2023.05.13 |
| 41. One-class Support Vector Machine(1-SVM)에 대하여 알아보자 with Python (0) | 2023.05.12 |
| 40. 인자 분석(Factor Analysis)에 대해서 알아보자 with Python (0) | 2023.05.03 |
| 39. 정준 상관 분석(Canonical Correlation Analysis)에 대해서 알아보자 with Python (6) | 2023.04.23 |





댓글