이번 포스팅에서는 모델 기반 이상치 탐지 방법론 중에 하나인 One-class Support Vector Machine(1-SVM)에 대해 알아보고자 한다. 여기에서는 One-class Support Vector Machine(1-SVM)의 개념과 파이썬 구현 방법을 소개한다.
- 목차 -
1. One-class Support Vector Machine(1-SVM)란 무엇인가?
이번 포스팅은 지도학습으로써의 서포트 벡터 머신 내용을 알면 도움이 된다. 이에 대한 내용은 아래 포스팅을 참고하면 된다.
19. 서포트 벡터 머신(Support Vector Machine)에 대해서 알아보자 with Python
19. 서포트 벡터 머신(Support Vector Machine)에 대해서 알아보자 with Python
딥러닝이 나타나기 전에 전성기를 구가했던 서포트 벡터 머신(Support Vector Machine)에 대해서 공부한 내용을 포스팅하려고 한다. 서포트 벡터 머신에 대한 개념과 종류 그리고 파이썬으로 구현하는
zephyrus1111.tistory.com
1. One-class Support Vector Machine(1-SVM)란 무엇인가?
1) 정의
One-class Support Vector Machine(1-SVM)은 하나의 클래스로 이루어진 데이터에 대해서 정상 데이터와 이상치를 나누는 평면을 찾는 비지도 학습 알고리즘이다.
2) 파헤치기
위의 정의를 좀더 살펴보자.
a. 1-SVM은 하나의 클래스를 정상과 이상치로 나누는 데 목적이 있다.
여기서 하나의 클래스란 불량과 정상과 같은 라벨을 사전에 모르는 상태를 말한다고 보면 된다. 1-SVM은 처음에는 모두 정상으로 보고(1-SVM에서 숫자 '1'은 One-class를 의미한다) 그중에서 돌발 행동을 하는 친구(이상치)와 대세를 따르는 친구(정상)를 나누는 평면을 구하는데 목적이 있는 것이다.
b. 1-SVM은 정상 데이터를 원점에서 최대한 멀게 하는 평면을 찾는다.
1-SVM은 정상 데이터는 원점과는 최대한 멀게 하는 평면을 찾으며 이 평면 아래에 있는 데이터는 이상치로 간주한다(아래 그림 참고).

2. 1-SVM 평면 추정 방법
이제 1-SVM에 대한 개념을 알았으니 평면을 찾는 방법에 대해서 알아보자. 먼저 아래 그림과 같이 10개의 데이터가 있다고 하자. 그러면 1-SVM은 이상치(빨간 점)와 정상(파란 점)을 구분하는 평면(초록색)을 찾는데 이때 원점과 최대한 멀리 떨어진 평면을 찾는다. 이는 정상 데이터를 최대한 떨어지게 하여 이상치와 구분하게 하기 위함이다.

이제 수식을 동원하여 1-SVM이 풀고자 하는 문제를 정리해 보자. 먼저 평면 방정식이 다음과 같다고 해보자. $$w^t\Phi(x)-\rho = 0 \tag{1}$$
이때 $w \in \mathbb{R}^q$이고 $x \in \mathbb{R}^p$는 $p$차원 데이터 $\Phi : \mathbb{R}^p \rightarrow \mathbb{R}^q$는 기존 $p$차원 데이터를 $q$차원으로 변환하는 매핑이다.
그리고 평면 또는 평면 위에 있는 점들은 정상, 평면 아래에 있는 점들을 이상치로 표현하기 위한 슬랙 변수 $\xi_i, i=1, \ldots, l$를 도입한다. 슬랙 변수 $\xi_i$ 평면 아래에 있으면 양수, 평면 또는 평면 위에 있으면 0 값을 갖는다. 이때 $\xi_i$는 이상치와 평면과의 거리라고 생각할 수 있다. 아래 그림은 위 그림을 수식으로 표현한 것이다.
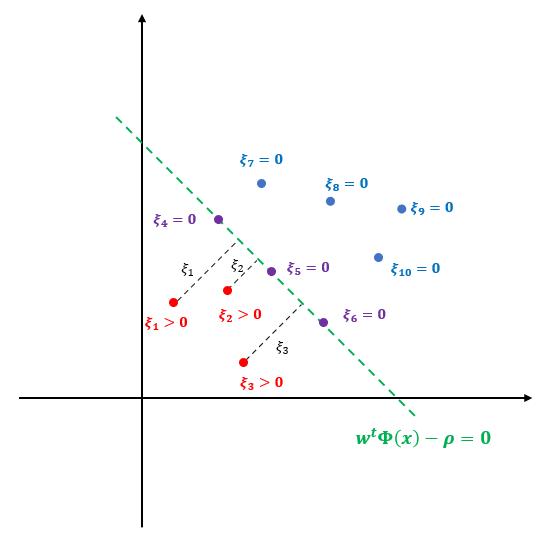
이때 모든 점 $x_i$에 대하여 다음이 성립하는 걸 알 수 있다.
$$w^t\Phi(x_i) -\rho \geq \xi_i, \xi_i \geq 0 \tag{2}$$
그리고 원점(매핑으로 변환된 후의 원점)과 경계사이의 거리 $d$는 다음과 같다.
$$ d = \frac{|-\rho|}{\| w\|_2} = \frac{\rho}{\| w\|_2} \tag{3}$$
이때 두 번째 등식에서 $\rho$는 일단 양수라고 생각하자(양수가 될 수밖에 없는 이유가 있는데 이는 아래에서 살펴본다). 1-SVM은 기본적으로 (3)을 최대화하는 평면을 찾는다. 이는 $\rho$를 최대화하고 $\|w\|_2$는 최소화하는 것과 같다. 이를 나중에 풀기 쉬운 Dual 문제로 바꾸기 위하여
$$\frac{1}{2}\|w\|_2^2-\rho \tag{4} $$
최소화하는 것으로 문제를 바꾼다. 그리고 슬랙 변수 $\xi_i$가 커져서 너무 많은 이상치를 발생시키지 않도록 (4)에 벌점항을 추가한다.
$$\frac{1}{2} \|w\|_2^2 -\rho - \frac{1}{vl}\sum_{i=1}^l\xi_i \tag{4} $$
여기서 $\nu \in (0,1]$이다.
마지막으로 제약 조건 (2)를 추가하면 1-SVM이 궁극적으로 풀고자하는 문제가 된다.
$$ \min_{w\in \mathbb{R}^q, \xi \in \mathbb{R}^l, \rho \in \mathbb{R}} \frac{1}{2} \|w\|_2^2 + \frac{1}{vl}\sum_{i=1}^l\xi_i-\rho \\ \text{subject to}\;\; w^t\Phi(x_i) \geq \rho-\xi_i, \xi_i \geq 0, \;\; \forall i=1, \ldots, l \tag{5}$$
이때 $\rho$를 양수로 제한하지 않는 이유에 대해서 궁금할 수 있는데 그럴 필요가 없는 이유를 아래에서 알아본다.
이제 평면을 구하는 방법을 알아보자. (5)를 Lagrangian으로 바꾸면 다음과 같다.
$$\small L(w, \xi, \rho, \alpha, \beta) = \frac{1}{2}\|w\|_2^2+\frac{1}{vl}\sum_{i=1}^l\xi_i-\rho -\sum_{i=1}^l\{ \alpha_i (w^t\Phi(x_i) -\rho +\xi_i) \} -\sum_{i=1}^l\beta_i\xi_i \tag{6}$$
여기서 $\alpha_i \geq 0, \beta_i \geq 0$이다.
KKT 조건의 Stationary 조건은 다음과 같다.
(Stationary)
$$\begin{align} \frac{\partial L}{\partial w} &= w-\sum_{i=1}^l\alpha_i\Phi(x_i) =0 \Rightarrow w = \sum_{i=1}^l\alpha_i\Phi(x_i) \tag{S.1} \\ \frac{\partial L}{\partial \xi_i} &= \frac{1}{vl} -\alpha_i-\beta_i=0, \;\; \forall i \Rightarrow \alpha_i = \frac{1}{vl}-\beta_i, \;\; \forall i \tag{S.2} \\ \frac{\partial L}{\partial \rho} &= -1+\sum_{i=1}^l\alpha_i \Rightarrow \sum_{i=1}^l\alpha_i=1 \tag{S.3} \end{align}$$
(6)을 (S.1)~(S.3)을 이용하면 다음과 같이 정리할 수 있다.
$$L(w, \xi, \rho, \alpha, \beta) = -\frac{1}{2} \sum_{i=1}^l\sum_{j=1}^l\alpha_i\alpha_j\Phi(x_i)^t\Phi(x_j) \tag{7}$$
원래는 $L$을 최대화해야 하지만 마이너스 부호가 있으므로 이를 제외하여 최소화하는 문제가 된다. 또한 서포트 벡터 머신에서는 복잡한 평면을 만들기 위해 커널 $k(x_i, x_j) = \Phi(x_i)^t\Phi(x_j)$을 고려하게 된다. 이를 반영하면 (5)의 Dual Problem은 다음과 같아진다.
$$\min_{\alpha \in \mathbb{R}^l} \frac{1}{2}\sum_{i=1}^l\sum_{j=1}^l\alpha_i\alpha_j k(x_i, x_j) \\ \text{subject to}\;\; 0\leq \alpha_i \leq \frac{1}{vl}, \sum_{i=1}^l\alpha_i=1 \tag{8} $$
(8)을 풀어서 나온 최적 $\alpha_i$에 대해서 다음의 KKT Complementary Slackness 조건을 만족해야 한다.
(Complementary Slackness)
$$\begin{align} \alpha_i\{ w^t \Phi(x_i) -\rho +\xi_i \} = 0, \;\; \forall i \tag{C.1} \\ \beta_i\xi_i = 0, \;\; \forall i\tag{C.2} \end{align}$$
(S.2)로부터 다음을 알 수 있다.
$$0\leq \alpha_i = \frac{1}{vl} - \beta_i \leq \frac{1}{vl} (\text{∵} \;\;\beta_i \geq 0) \\ \Rightarrow 0 \leq \alpha_i \leq \frac{1}{vl}$$
이제 $\alpha_i$ 값에 따른 데이터의 범주를 생각해 보자.
Case 1) $\alpha_i = 0$
$$\begin{align} \alpha_i = 0 & \Rightarrow \beta_i = \frac{1}{vl} \neq =0 \;\;\text{∵} \;\; \text{(S.2)} \\ & \Rightarrow \xi_i = 0\;\; \text{∵} \;\; \text{(C.2)} \\ & \Rightarrow w^t\Phi(x_i) \geq \rho \;\; \text{∵} \;\; \text{Constraint} \end{align}$$
따라서 이 경우는 데이터 $x_i$가 초평면 경계에 있거나 초평면보다 위에 있는 경우다(왼쪽 그림).
Case 2) $\alpha_i = \frac{1}{vl}$
$$\begin{align} \alpha_i = \frac{1}{vl} \Rightarrow \beta_i = 0\;\;\text{∵} \;\; \text{(S.2)} \end{align}$$
이 경우 자동적으로 (C.2)를 만족하게 되므로 $\xi_i > 0$ 또는 $\xi_i=0$이 된다.
이때 (C.1)에 의하여 $w^t\Phi(x_i)=\rho-\xi_i$가 된다.
$\xi_i=0$이면 $w^t\Phi(x_i) =\rho$이므로 $x_i$는 초평면 경계에 있게 된다. 만약 $\xi_i>0$이면 $\xi_i$의 정의에 의하여 $x_i$는 초평면보다 아래에 있게 된다(가운데 그림).
Case 3) $0<\alpha_i <\frac{1}{vl}$
$$\begin{align} 0 < \alpha_i <\frac{1}{vl} & \Rightarrow \beta_i > 0 \;\; \text{∵} \;\; \text{(S.2)} \\ & \Rightarrow \xi_i = 0 \;\; \text{∵} \;\; \text{(C.2)} \end{align}$$
또한 (C.1)에 의하여
$$w^t\Phi(x_i) = \rho - \xi_i = \rho$$
이므로 $x_i$는 정확히 초평면 위에 있게 된다(오른쪽 그림).
이때 초평면 위에 있는 데이터를 서포트 벡터(Support Vector)라 한다.
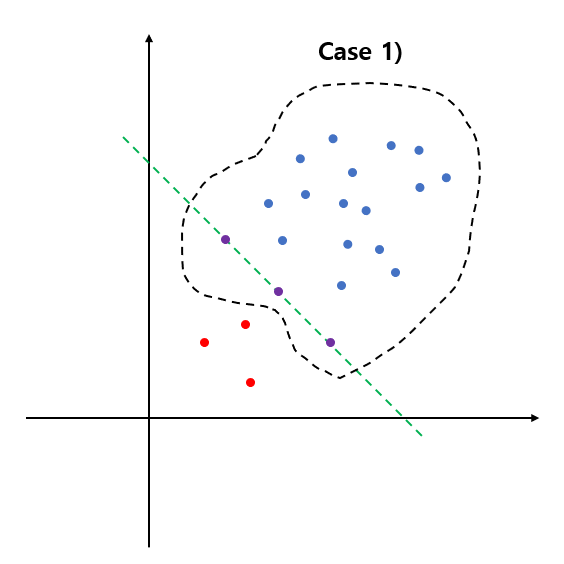


(8)을 풀어서 최적 $\alpha_i$를 계산하면 이상치와 정상은 아래의 의사결정 함수(Decision Function)을 이용하여 결정한다.
$$\begin{align} f(x) &= \text{sign} ( w^t\Phi(x) -\rho) \\ &= \text{sign} \left (\sum_{i=1}^l\alpha_i\Phi(x_i)^t\Phi(x) -\rho \right ) \\ &= \text{sign} \left (\sum_{i=1}^l\alpha_ik(x_i, x) -\rho \right ) \end{align} \tag{9}$$
이때 $f(x)=-1$이면 이상치 $f(x)=1$이면 정상으로 판단한다. Case 3) 일 때 $w^t\Phi(x_i)=\rho$ 이므로 $\rho$는 다음과 같이 추정할 수 있다.
$$\rho = \frac{1}{\text{#}\{ i : 0<\alpha_i < \frac{1}{vl} \} } \sum_{i : 0<\alpha_i < \frac{1}{vl}} \sum_{j=1}^l\alpha_jk(x_i, x_j) \tag{10}$$
1-SVM의 특징
a. 가우시안 커널(Gaussian Kernel)
1-SVM에서 사용하는 커널은 가우시안 커널이다.
$$k(x_i, x_j) = \exp \left ( -\frac{\|x-y\|_2^2}{c} \right ), c > 0$$
이는 (매핑으로 변환된) 모든 데이터들의 내적을 모두 양수로 만들며 이는 모든 데이터들이 아래와 같이 한 사분면에 포함될 수 있게 한다.
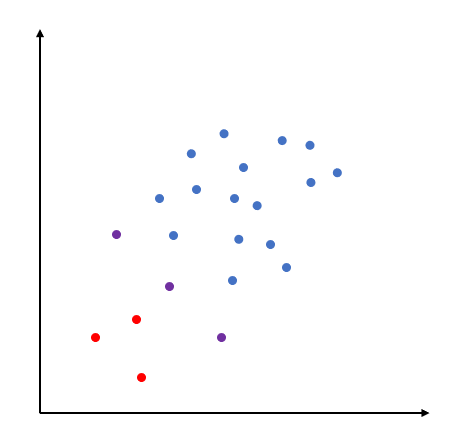
즉, 데이터를 커널을 이용하여 한 사분면에 있는 것처럼 취급하고 원점에서 최대한 멀리 떨어지게하는 평면을 찾는 것이 1-SVM의 핵심 아이디어인 것이다.
또한 가우시안 커널을 사용하게 됨으로써 (10)에서 최적 $\rho$는 음이 아닌 실수가 된다. 따라서 $\rho$를 양수로 취급할 수 있는 것이며 최적화 문제에서 굳이 제약을 하지 않았던 것이다.
b. $\nu$의 성질
Schölkopf는 One-class SVM에서 $\nu$의 다음과 같은 성질을 밝혔다.
(1) 전체 데이터에 대한 이상치 범주의 비율의 상한은 $\nu$이다.
(2) 전체 데이터에 대한 SV의 비율의 하한은 $\nu$이다.
즉, $\nu$는 서포트 벡터와 이상치의 개수를 컨트롤할 수 있다는 것이다.
3. 파이썬 구현
이제 One-class SVM을 파이썬으로 구현해 보자. 아래 코드에서 OneClassSVM 클래스는 초기값으로 $\nu, c$를 받은 뒤 fit 메서드를 통하여 $\rho$와 $\alpha$를 추정한다. 이때 Convex Optimization을 수행하는 cvxopt 모듈을 사용했다.
import numpy as np
from cvxopt import matrix, solvers
class OneClassSVM:
def __init__(self, nu=0.5, c=1):
self.nu = nu
self.c = c
self.rho = None
self.alpha = None
self.X = None
def gaussian_kernel(self, x, y, c):
return np.exp(-np.sum(np.square(x-y))/c)
def make_kernel_matrix(self, X, c):
n = X.shape[0]
Q = np.zeros((n,n))
q_list = []
for i in range(n):
for j in range(i, n):
q_list.append(self.gaussian_kernel(X[i, ], X[j, ], c))
Q_idx = np.triu_indices(len(Q))
Q[Q_idx] = q_list
Q = Q.T + Q - np.diag(np.diag(Q))
return Q
def fit(self, X):
nu = self.nu
c = self.c
Q = self.make_kernel_matrix(X, c)
n = X.shape[0]
P = matrix(Q)
q = matrix(np.zeros((n,1)))
G = matrix(np.vstack([-np.eye(n), np.eye(n)]))
h = matrix(np.hstack([np.zeros(n), np.ones(n)*(1/(nu*n))]))
A = matrix(np.ones((1, n)))
b = matrix(np.ones(1))
solvers.options['show_progress'] = False
sol = solvers.qp(P, q, G, h, A, b)
alphas = np.array(sol['x'])
rho = 0
alphas = alphas.flatten()
S = ((alphas>1e-3)&(alphas<(1/(nu*n))))
S_idx = np.where(S)[0]
for s in S_idx:
temp_vect = np.array([alphas[i]*self.gaussian_kernel(X[i], X[s, ], c) for i in range(n)])
rho += np.sum(temp_vect)/np.sum(S)
self.rho = rho
self.alphas = alphas
self.X = X
return self
def predict(self, X):
return np.array([np.sign(self._predict(x)) for x in X])
def _predict(self, x):
X = self.X
n = X.shape[0]
alphas = self.alphas
rho = self.rho
c = self.c
temp_vect = np.array([alphas[i]*self.gaussian_kernel(X[i], x, c) for i in range(n)])
decision_val = np.sum(temp_vect)-rho
return decision_val4. 예제
여기서는 시뮬레이션용 데이터를 이용하여 실험을 진행해 본다. Scikit-Learn(sklearn)에서 제공하는 make_classification을 이용하여 시뮬레이션용 데이터를 만들었다.
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False
from cvxopt import matrix, solvers
from sklearn.datasets import make_classification
## 실험용 데이터
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2,
n_redundant=0, n_repeated=0, n_classes=2,
n_clusters_per_class=1,
weights=[0.995, 0.005],
class_sep=0.5, random_state=0)
이제 위에서 만든 데이터를 이용하여 One-class SVM 모형을 만들어보자 그러고 나서 이상치와 정상 라벨을 예측해 보자. $\nu, c$의 여러 조합을 봐야겠지만 여기서는 $\nu=0.1, c=1$로 설정했다.
oc_svm = OneClassSVM(nu=0.1, c=1).fit(X)
labels = oc_svm.predict(X) ## -1은 이상치, 1은 정상으로 예측하기
예측 결과를 시각화해 보자.
fig = plt.figure(figsize=(10, 10))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(X[:, 0], X[:, 1], c=labels)
plt.show()

코드를 실행하면 노란색은 정상, 이상치는 보라색으로 표현된 시각화 결과를 얻을 수 있다. 결과가 나름 합리적인 듯하다.
5. 장단점
One-class SVM의 장단점은 다음과 같다.
- 장점 -
a. One-class SVM은 비지도 학습으로 이상치를 탐지하는 데 있어서 라벨이 필요하지 않다.
b. 태생이 서포트 벡터 머신이므로 커널을 이용하여 이상치와 정상을 구분하는 복잡한 비선형 경계를 학습할 수 있다.
c. 다른 이상치 탐지 알고리즘과 비교하여 과적합의 영향을 덜 받는다.
One-class SVM은 평면을 최대한 멀리 떨어지게 하고 $\nu$를 이용하여 이상치의 개수를 적절하게 컨트롤하여 이상치에 과도하게 영향을 받지 않게 할 수 있다.
- 단점 -
a. Hyper Parameter 튜닝을 잘해줘야 한다.
One-class SVM은 최적화에서 $\nu$, 가우시안 커널의 $c$를 교차 검증을 잘 이용하여 튜닝을 해야 한다.
b. 대용량 데이터에서 계산량이 많아질 수 있다.
그에 따라 학습 시간이 오래 걸리고 메모리도 많이 잡아먹을 수 있다.
c. 이상치 탐지의 성능을 제대로 평가하기 위해선 다른 알고리즘의 성능과 비교해 보는 것이 좋다.
요즘 한창 이상치 탐지에 관심이 생겨서 관련 방법을 공부하고 있다. 인생은 짧고 배울 것은 많다는 것을 다시한 번 느낀다.
- 참고 자료 -
Schölkopf - Estimating the Support ofj a Hight-dimensional Distribution
강필성 - 03-6: Anomaly Detection - Auto-Encoder, 1-SVM, & SVDD
'통계 > 머신러닝' 카테고리의 다른 글
| 43. Support Vector Data Description(SVDD)에 대해서 알아보자 with Python (4) | 2023.05.13 |
|---|---|
| 42. Local Outlier Factor(LOF)에 대해서 알아보자 with Python (0) | 2023.05.13 |
| 40. 인자 분석(Factor Analysis)에 대해서 알아보자 with Python (0) | 2023.05.03 |
| 39. 정준 상관 분석(Canonical Correlation Analysis)에 대해서 알아보자 with Python (6) | 2023.04.23 |
| 38. 부분 최소 제곱 회귀(Partial Least Square Regression : PLSR)에 대해서 알아보자 with Python (5) | 2023.04.08 |





댓글