지난 포스팅에서는 클러스터링(군집화) 평가 지표로써 Dunn Index, Silhouette Index에 대해서 알아보았다. 이번엔 그 외 평가 지표인 Calinski-Harabasz index, Davies-Bouldin index, Rand Index에 대해서 알아보고 파이썬으로 구현하는 방법도 소개하고자 한다. Dunn Index와 Silhouette Index에 대한 내용은 아래 포스팅을 참고하기 바란다.
12. 클러스터링(군집화) 평가 지표 Dunn Index with Python
14. 클러스터링(군집화) 평가지표 Silhouette(실루엣) 지수(계수)에 대해서 알아보자 with Python
- 목차 -
Calinski-Harabasz index
1) 정의
먼저 데이터 $\{x_1, \ldots, x_n \}$이 있다고 하자. 여기서 $x_i \in \mathbb{R}^p$는 $p$차원 벡터이다. 이 데이터들이 클러스터링 알고리즘(예: K-Means, Gaussian Mixture Model)에 의하여 클러스터가 부여되었다고 해보자. 총클러스터는 $K$개이고 $c_k, k=1, \ldots, K$를 클러스터의 중심 벡터, $n_k$를 클러스터에 속하는 데이터 개수 그리고 $c = \sum_{i=1}^nx_i/n$은 전체 데이터의 중심 벡터라고 하자.
Calinski-Harabasz index $CH$의 정의는 다음과 같다.
$$CH = \left[ \frac{\sum_{k=1}^Kn_k \|c_k - c\|_2^2 }{K-1} \right] / \left[ \frac{\sum_{k=1}^K\sum_{i=1}^{n_k} \| x_i^k-c_k \|_2^2}{n-K} \right ]$$
여기서 $x_i^k, i=1, \ldots, n_k$는 $k$번째 클러스터에 속한 데이터를 의미하며 $\|a\|_2$는 $p$차원 유클리디안 거리(Euclidean Distance)이다.
$CH$의 분자는 군 간 변동(Variation Between Cluster), 분모는 군 내 변동(Variation Within Cluster)로 이루어져 있다. 만약 클러스터링이 잘되었다면 각 클러스터끼리는 최대한 떨어져 있어야 할 것이다. 즉, 군 간 변동은 커야 할 것이다. 반대로 클러스터 내 데이터끼리는 잘 뭉쳐져 있어야 하므로 군 내 변동은 작아야 할 것이다. 따라서 $CH$ 값이 클수록 클러스터링(군집화)이 잘되었다고 할 수 있다. $CH$는 클러스터링 알고리즘간 결과 비교를 가능하게 한다. 즉, $CH$값을 가장 크게 하는 클러스터 알고리즘이 좋다고 할 수 있다. 또한 클러스터 개수를 모를 때 $K$를 1부터 하나씩 증가시켜 가며 $CH$를 계산하고 이를 가장 크게 하는 $K$를 최종 클러스터 개수로 선택할 수 있다.
2) 파이썬 예제
이제 Calinski-Harabasz index를 파이썬으로 계산해보자. 아래 get_calinski_harabasz_index 함수는 데이터와 클러스터 라벨을 받아서 Calinski-Harabasz index를 계산한다. 설명은 주석을 참고하기 바란다.
def get_calinski_harabasz_index(X, cluster):
cluster_label = np.unique(cluster) ## 클러스터 라벨
K = len(cluster_label) ## 총 클러스터 개수
n = X.shape[0] ## 총 데이터 개수
c = np.mean(X, axis=0) ## 전체 데이터 중심 벡터
num_sum = 0 ## calinski_harabasz_index 분자
denom_sum = 0 ## calinski_harabasz_index 분모
for cl in cluster_label:
sub_X = X[np.where(cluster==cl)[0], :]
c_k = np.mean(sub_X, axis=0)
n_k = sub_X.shape[0]
num_sum += n_k*np.sum(np.square(c_k-c))
denom_sum += np.sum(np.square(sub_X-c_k))
## calinski_harabasz_index
calinski_harabasz_index = (num_sum/(K-1))/(denom_sum/(n-K))
return calinski_harabasz_index
이제 샘플 데이터를 이용하여 Calinski-Harabasz index를 계산해보자. 나는 3개의 군집을 갖는 데이터를 생성해 주었다.
import numpy as np
import random
import matplotlib.pyplot as plt
np.random.seed(100)
size = 50
x_11 = np.linspace(0.3,0.8,20)
x_12 = np.linspace(1.4,1.9,15)
x_13 = np.linspace(2.5,3.1,15)
x1 = np.concatenate((x_11,x_12,x_13),axis=None)
error = np.random.normal(1,0.5,size)
x2 = 1.5*x1+2+error
fig = plt.figure(figsize=(7,7))
fig.set_facecolor('white')
plt.scatter(x1, x2, color='k')
plt.show()
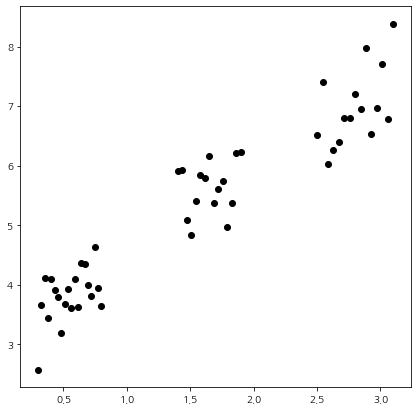
이제 K-Means 클러스터링 알고리즘을 이용하여 군집화를 수행한다. 군집의 개수는 3으로 설정했다.
from sklearn.cluster import KMeans
X = np.c_[x1, x2]
kmeans = KMeans(n_clusters=3, random_state=0).fit(X)
cluster = kmeans.predict(X)
이제 Calinski-Harabasz index를 계산해보자
print(get_calinski_harabasz_index(X, cluster))

222.79 정도가 나왔다. Scikit-Learn에서도 Calinski-Harabasz index를 계산할 수 있다.
from sklearn.metrics import calinski_harabasz_score
print(calinski_harabasz_score(X, cluster))

코드를 실행하면 구현한 것과 동일한 값을 출력하는 것을 알 수 있다.
이번에는 클러스터 개수를 2~5까지 변화시키면서 Calinski-Harabasz index가 어떻게 변하는지 살펴보자.
n_cluster_list = [2,3,4,5]
X = np.c_[x1, x2]
chi_list = []
for n_cluster in n_cluster_list:
kmeans = KMeans(n_clusters=n_cluster, random_state=0).fit(X)
cluster = kmeans.predict(X)
chi_list.append(get_calinski_harabasz_index(X, cluster))
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.plot(n_cluster_list, chi_list)
ax.set_xticks(n_cluster_list)
plt.show()
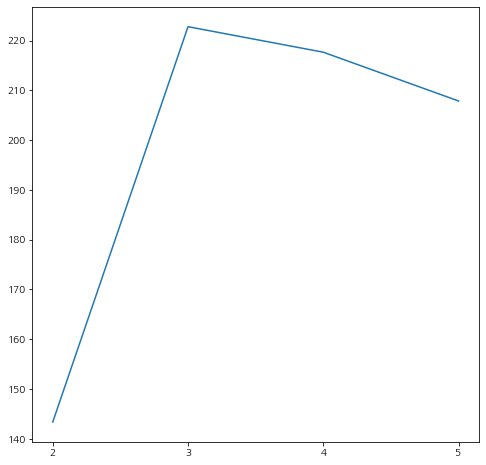
클러스터 개수가 3일 때 Calinski-Harabasz index가 최대인 것을 알 수 있다. 따라서 데이터를 만들 때 의도했던 대로 적정 클러스터 개수는 3을 정확히 맞춘 것을 알 수 있다.
3) 장단점
Calinski-Harabasz index의 장단점은 다음과 같다.
- 장점 -
a. 변동이라는 개념을 도입한 직관적인 클러스터링 평가 지표이다.
클러스터링이 잘되어 있을수록 군 내 변동은 작고 군 간 변동은 커지는 것을 직관적으로 알 수 있으므로 굉장히 합리적인 평가 지표라 할 수 있다.
b. 클러스터링 알고리즘 간 비교를 가능하게 한다.
어떠한 클러스터링 알고리즘이든 계산이 가능하므로 클러스터링 알고리즘 간 결과 비교에도 $CH$를 사용할 수 있다.
c. 클러스터링 개수를 모르는 경우 클러스터 개수를 선택하는데 활용할 수 있다.
d. 계산이 쉽고 빠르다.
실루엣 지수(Siloutette Index)에 비하여 계산 과정이 쉽고 빠르다.
- 단점 -
a. 이상치에 민감하다.
클러스터 중심과의 거리를 이용하므로 이상치 유무에 따라 결과 해석이 어려울 수 있다.
b. DBSCAN과 같은 밀도 기반 클러스터링 알고리즘의 평가 척도로는 적절하지 않다.
중심을 업데이트하는 방식으로 클러스터링을 수행하는 알고리즘(K-Means, Gaussian Mixture Model)에 대한 평가 지표로는 $CH$가 적절하지만 밀도 기반 클러스터링 알고리즘인 DBSCAN에 대해서는 적절하지 않은 평가 지표이다.
Davies-Bouldin index
1) 정의
먼저 데이터 $\{x_1, \ldots, x_n \}$이 있다고 하자. 여기서 $x_i \in \mathbb{R}^m$는 $m$차원 벡터이다. 클러스터링 알고리즘(예: K-Means, Gaussian Mixture Model)을 이용하여 데이터들에 클러스터가 할당되어 있다고 해보자. 총클러스터는 $K$개이고 $c_k, k=1, \ldots, K$를 클러스터의 중심 벡터, $n_k$를 클러스터에 속하는 데이터 개수라 하자. 이때 다음을 정의한다.
$$\begin{align}S_k &= \left( \frac{1}{n_k}\sum_{i=1}^{n_k}\| x_i^k-c_k \|_p^q \right)^{1/q} \\ M_{k, l} &= \|c_k - c_l\|_p = \left ( \sum_{j=1}^m|c_{k, j} - c_{l, j}|^p \right )^{1/p} \end{align}$$
여기서 $\|a\|_p$은 $L_p$-Norm이다. 이때 $q = 1, p=2$를 주로 사용한다.
$S_k$는 $k$번째 군 내 변동으로 해석할 수도 있겠지만 $k$번째 군 내 데이터들 간의 비슷한 정도를 나타내는 유사도(Similarity)의 역수로 해석할 수 있다. $S_k$는 군 내 변동이므로 그 값이 작을수록 좋다. $M_{k, l}$은 $k$번째 군과 $l$번째 군 간의 차이를 측정하는 측도가 된다. 따라서 $M_{k, l}$ 값은 클수록 좋다.
이제 두 클러스터 $k, l$의 군집화가 얼마나 잘되었는지를 알려주는 측도 $R_{k, l}$을 정의하자.
$$R_{k, l} = \frac{S_k+S_l}{M_{k, l}}$$
$R_{k,l}$의 성질을 잠깐 살펴보자.
1) $R_{k, l}\geq 0$
2) $R_{k, l} = R_{l, k}$
3) 만약 $M_{k, l} = M_{k, l'}$이고 $S_{l'}\geq S_{l}$이라면 $R_{k, l'} \geq R_{k, l}$
4) 만약 $S_{l'}=S_{l}$이고 $M_{k, l'} \geq M_{k, l}$이라면 $R_{k, l'} \geq R_{k, l}$
1)은 $R(=R_{k, l})$이 항상 음이 아닌 정수이며 이는 $R$ 비교 지표로써 유용한 성질을 갖고 있는 것이다. 왜냐하면 음수는 신경을 안 써도 되기 때문이다. 2)는 $R$이 대칭성을 갖고 있다는 것이며 $k$번째 군과 $l$번째 군의 순서에 따라 $R$ 값이 바뀌지 않는 것으로 상식적이다. 3)은 같은 군 간 변동(Between Cluster)이라면 군 내(Within Cluster) 변동이 작을수록 $R$값 또한 작아진다는 것이며 4)는 같은 군 내 변동이라면 군 간 변동이 클수록 $R$값이 작아진다. 3), 4)의 성질로 인하여 $R$은 두 클러스터(군)가 군집화가 잘되어있는지 알아보는 측도라 할 수 있다. $R$의 값은 작을수록 두 클러스터의 군집화가 잘되어있다고 판단한다.
이제 $D_k$를 정의하자.
$$D_k = \max_{l \neq k}R_{k, l}$$
$D_k$는 $k$번째 클러스터와 군집화가 가장 안되어있는 경우(Worst Case)를 나타낸다고 할 수 있다. 이제
Davies-Bouldin index $DB$는 다음과 같이 정의한다.
$$DB = \frac{1}{K}\sum_{k=1}^KD_k$$
$DB$는 모든 클러스터에 대하여 군집화가 가장 안되어있는 평균적인 경향을 나타내고 그 값이 클수록 군집화가 잘 안 되어 있고 작을수록 군집화가 잘되어있다고 판단한다.
2) 파이썬 예제
이제 Davies-Bouldin index을 파이썬으로 계산해 보자. 아래 get_davies_bouldin_index 함수는 Davies-Bouldin index를 계산한다. 앞에서 정의한 수식을 그대로 구현한 것이다. 이때 $q=1, p=2$를 사용했다.
def get_davies_bouldin_index(X, cluster):
def get_similarity(X, cluster, cluster_label): ## 군 내 변동 계산
sub_X = X[np.where(cluster==cluster_label)[0], :]
c_k = np.mean(sub_X, axis=0)
n_k = sub_X.shape[0]
similarity = np.mean(np.linalg.norm(sub_X-c_k, axis=1))
return similarity
def get_separation(X, cluster, cluster1, cluster2): ## 군 간 변동 계산
sub_X1 = X[np.where(cluster==cluster1)[0], :]
sub_X2 = X[np.where(cluster==cluster2)[0], :]
c1 = np.mean(sub_X1, axis=0)
c2 = np.mean(sub_X2, axis=0)
separation = np.linalg.norm(c1-c2)
return separation
def get_R(X, cluster, cluster1, cluster2): ## R 계산
S1 = get_similarity(X, cluster, cluster1)
S2 = get_similarity(X, cluster, cluster2)
M = get_separation(X, cluster, cluster1, cluster2)
R = (S1+S2)/M
return R
## D 계산
D_list = []
uniq_cluster = np.unique(cluster)
for uc in uniq_cluster:
remainder = list(set(uniq_cluster)-{uc})
R_list = []
for r in remainder:
R = get_R(X, cluster, uc, r)
R_list.append(R)
D_list.append(max(R_list))
davies_bouldin_index = np.mean(D_list)
return davies_bouldin_index
이제 앞에서 생성한 데이터를 K-Means 클러스터링 알고리즘(군집 개수 3)으로 군집화 한 다음 Davies-Bouldin index를 계산해보자.
from sklearn.cluster import KMeans
X = np.c_[x1, x2]
kmeans = KMeans(n_clusters=3, random_state=0).fit(X)
cluster = kmeans.predict(X)
print(get_davies_bouldin_index(X, cluster))

Scikit-Learn에서도 Davies-Bouldin index를 계산할 수 있다.
from sklearn.metrics import davies_bouldin_score
print(davies_bouldin_score(X, cluster))

직접 구현한 것과 동일한 결과를 출력한다. 이번에는 클러스터 개수를 2~5까지 변화시키면서 Davies-Bouldin index가 어떻게 변하는지 살펴보자.
n_cluster_list = [2,3,4,5]
X = np.c_[x1, x2]
dbi_list = []
for n_cluster in n_cluster_list:
kmeans = KMeans(n_clusters=n_cluster, random_state=0).fit(X)
cluster = kmeans.predict(X)
dbi_list.append(davies_bouldin_score(X, cluster))
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.plot(n_cluster_list, dbi_list)
ax.set_xticks(n_cluster_list)
plt.show()
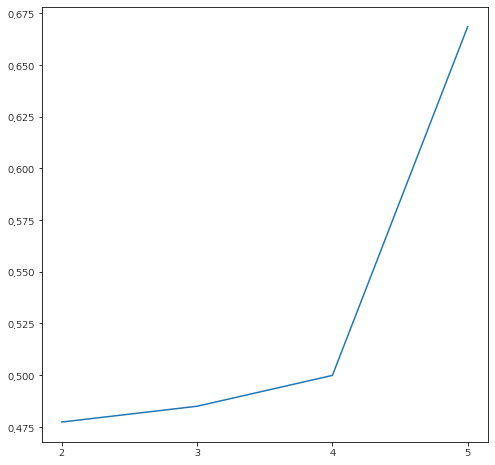
!! 우리의 예상과 다르게 클러스터 개수가 2개일 때 Davies-Bouldin index이 제일 작게 나왔다. 그러면 한번 클러스터 개수가 2인 경우와 3인 경우 클러스터 결과를 살펴보자.
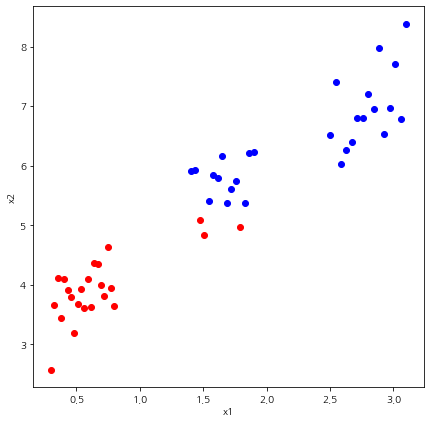
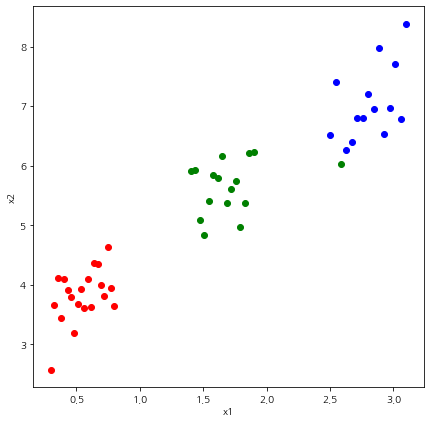
위 그림에서 왼쪽인 클러스터 개수가 2인 경우, 오른쪽이 3인 경우다. 오른쪽을 보면 초록점 하나가 파란색 군집에 포함된 것을 알 수 있다. 이 부분 때문에 Davies-Bouldin index의 값이 증가한 것이다. 따라서 이를 보정하기 위하여 클러스터가 3인 경우 초기 시작점을 따로 설정해 주었다.
kmeans = KMeans(n_clusters=3, random_state=0, init=np.array([[0.5, 3.9], [1.7,5.5], [2.7,7]])).fit(X)
cluster = kmeans.predict(X)
print(get_davies_bouldin_index(X, cluster))
fig = plt.figure(figsize=(7,7))
fig.set_facecolor('white')
for i, c in enumerate(cluster):
if c == 0:
color = 'blue'
elif c ==1:
color = 'red'
elif c==2:
color = 'green'
plt.scatter(X[i,0],X[i,1], color=color)
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()

클러스터링이 깔끔하게 된 것을 알 수 있다. 이러한 경우를 반영하여 다시 Davies-Bouldin index를 다시 계산해 보자.
n_cluster_list = [2,3,4,5]
X = np.c_[x1, x2]
dbi_list = []
for n_cluster in n_cluster_list:
if n_cluster != 3:
kmeans = KMeans(n_clusters=n_cluster, random_state=0).fit(X)
else:
kmeans = KMeans(n_clusters=3, random_state=0, init=np.array([[0.5, 3.9], [1.7,5.5], [2.7,7]])).fit(X)
cluster = kmeans.predict(X)
dbi_list.append(get_davies_bouldin_index(X, cluster))
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.plot(n_cluster_list, dbi_list)
ax.set_xticks(n_cluster_list)
plt.show()
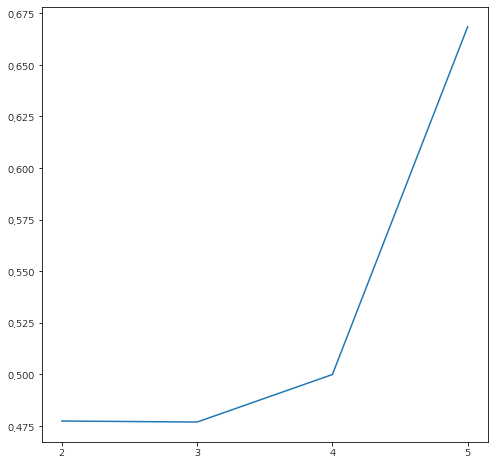
그림에서 알 수 있듯이 클러스터 개수가 3인 경우에 Davies-Bouldin index가 최소가 되는 것을 알 수 있다.
3) 장단점
Davies-Bouldin index의 장단점은 다음과 같다.
- 장점 -
a. 계산이 간단하다.
실루엣 지수(Siloutette Index)에 비하여 계산 과정이 간단하다.
b. Calinski-Harabasz index와 마찬가지로 변동이라는 개념을 도입한 직관적인 클러스터링 평가 지표이다.
클러스터링이 잘되어 있을수록 군 내 변동은 작고 군 간 변동은 커지는 것을 직관적으로 알 수 있으므로 굉장히 합리적인 평가 지표라 할 수 있다.
c. 클러스터링 알고리즘 간 비교를 가능하게 한다.
클러스터링 알고리즘에 관계없이 계산이 가능하므로 클러스터링 알고리즘 간 결과 비교에도 $DB$를 사용할 수 있다.
d. 클러스터링 개수가 알려져 있지 않은 상황에서 계산하는데 활용할 수 있다.
- 단점 -
a. 이상치에 민감하다.
Calinski-Harabasz index와 마찬가지로 이상치 유무에 따라 결과 해석이 어려울 수 있다.
b. 선택해야 하는 파라미터들이 있다.
Davies-Bouldin index는 $p, q$와 같은 Norm의 계수를 설정해줘야 하며 이론적인 선택 방법은 없는 것 같다. 보통 $q=1, p=2$를 쓴다고 한다(위키).
c. 클러스터링 알고리즘 초기 중심치에 따라 결과가 뒤 바뀔 수 있다.
파이썬 예제에서 살펴보았듯이 초기 중심치에 따라 Davies-Bouldin index 값이 차이가 많이 발생할 수 있다.
d. DBSCAN과 같은 밀도 기반 클러스터링 알고리즘의 평가 척도로는 적절하지 않다.
Calinski-Harabasz index와 마찬가지로 밀도 기반 클러스터링 알고리즘인 DBSCAN에 대해서는 적절하지 않은 평가 지표이다.
- 참고 자료 -
https://www.geeksforgeeks.org/calinski-harabasz-index-cluster-validity-indices-set-3/
'통계 > 머신러닝' 카테고리의 다른 글
| 35. Spline Regression에 대해서 알아보자 with Python (2) | 2023.02.19 |
|---|---|
| 34. ROC(Receiver Operating Characteristic) 곡선과 AUC(Area Under the Cuve)에 대해서 알아보자 with Python (0) | 2023.02.02 |
| 32. Gain Chart와 Lift Chart에 대해서 알아보자 with Python (0) | 2023.01.17 |
| 31. 지도 학습 모형 성능 지표에 대해서 알아보자 with Python (2) | 2023.01.13 |
| 30. DBSCAN에 대해서 알아보자 with Python (0) | 2022.11.03 |





댓글