이번 포스팅에서는 R 패키지인 Boruta의 변수 선택 알고리즘에 대한 개념을 알아보고자 한다.
- 목차 -
이번 포스팅은 랜덤 포레스트(Random Forest)의 대한 개념을 알아야 이해하는데 수월하다. 랜덤 포레스트(Random Forest)에 대한 개념을 잘 모르는 분들은 아래 포스팅을 참고하면 이해하는데 도움이 될 것이다.
24. 랜덤 포레스트(Random Forest)에 대해서 알아보자
24. 랜덤 포레스트(Random Forest)에 대해서 알아보자
이번 포스팅에서는 랜덤 포레스트(Random Forest)에 대해서 알아보고자 한다. 랜덤 포레스트(Random Forest)의 개념, 알고리즘, 여러 고려사항 및 장단점에 대해서 정리해보려고 한다. - 목차 - 1. 랜덤 포
zephyrus1111.tistory.com
1. Boruta란 무엇인가?
1) 정의
Boruta는 랜덤 포레스트 기반 변수 선택 알고리즘을 구현한 R 패키지 이름이다. Boruta가 구현한 변수 선택 알고리즘은 원래 데이터와 이들의 Permutation 버전인 쉐도우 변수 데이터를 이용하여 랜덤 포레스트 모형을 학습하며 "중요한 변수라면 쉐도우 변수들의 중요도보다는 높을 것이다"라는 아이디어에 착안하여 만들어진 것이다.
2) 파헤치기
Boruta가 구현한 변수 선택 알고리즘의 정의를 하나씩 파헤쳐보자. Boruta는 R 패키지 이름이지만 지금부터는 Boruta의 변수 선택 알고리즘을 줄여서 Boruta라고 하겠다.
a. Boruta는 랜덤포레스트 기반으로 만들어진 변수 선택 알고리즘이며 랜덤 포레스트 학습 시 쉐도우 변수 데이터를 이용한다.
먼저 주어진 변수의 쉐도우 변수란 해당 변수 데이터(데이터에서 하나의 칼럼)를 Permutation하여Permutation 하여 얻어진 변수 데이터를 말하며 쉐도우 변수 데이터는 원래의 데이터에서 모든 변수를 개별적으로 Permutation 하여 얻어진 데이터를 말한다.
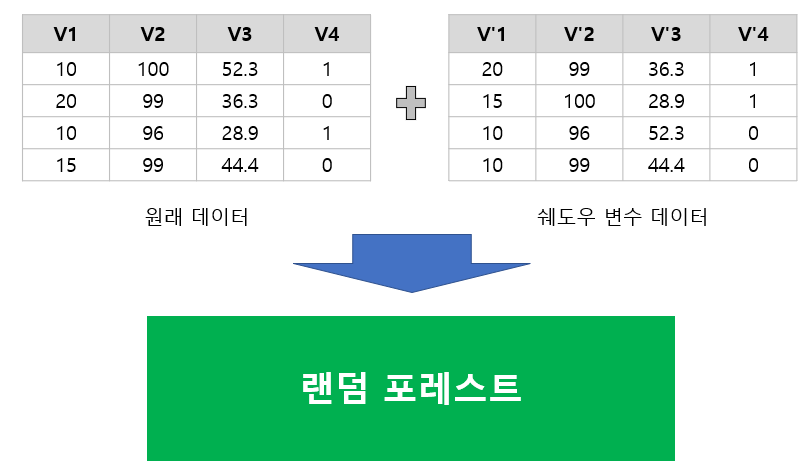
아래 표는 원래 데이터(왼쪽)와 쉐도우 변수 데이터(오른쪽)의 예를 나타낸 것이다.

Boruta는 원래 데이터와 쉐도우 변수 데이터를 같이 넣고 랜덤 포레스트 모형을 학습한다. 왜냐하면 원래 변수와 쉐도우 변수의 중요도를 동시에 비교하기 위해서이다.
b. Boruta는 랜덤 포레스트 모형을 학습하며 "중요한 변수라면 쉐도우 변수들의 중요도보다는 높을 것이다"라는 아이디어에 착안하여 만들어진 것이다.
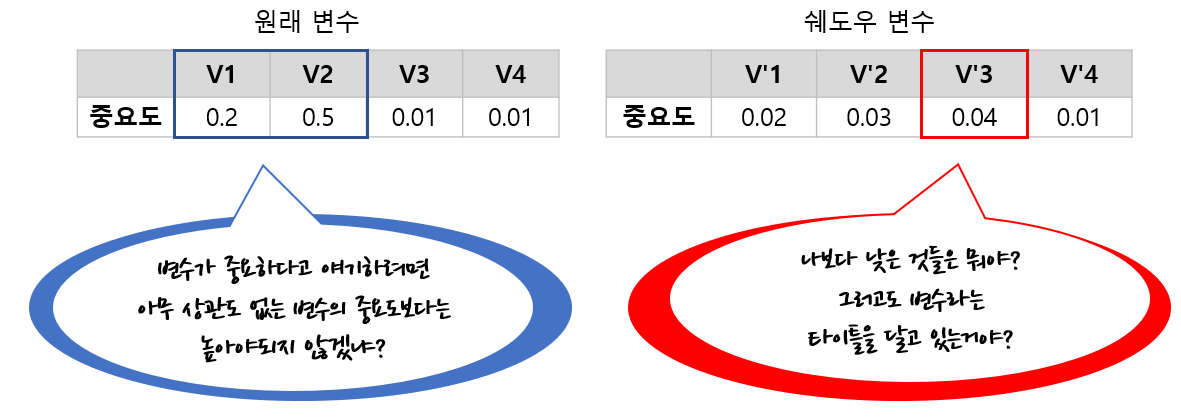
Boruta는 랜덤 포레스트 모형에 대하여 원래 변수와 쉐도우 변수의 중요도를 계산한다. 이때 변수를 선택한다는 것은 중요한 변수를 선택한다는 것이고 이를 위해 어느 변수가 중요한지를 계산해야한다. Boruta는 쉐도우 변수 중요도의 최대값보다 큰 변수 중요도를 갖는 원래 변수를 중요하다고 판단한다. 즉, Boruta의 철학은 Permutation을 통해서 아무 관련성 없어 보이는 일종의 가짜 변수들의 중요도보다는 높아야 변수들이 중요하다는 것이다. 아래 그림은 Boruta에서 중요한 변수를 선택하는 원리를 나타낸 것이다.
2. Boruta 변수 선택 알고리즘
1) 변수 중요도 계산 및 비교
Boruta는 랜덤 포레스트를 이용하여 중요 변수를 선택한다. 이를 위해 변수들(원래 변수+쉐도우 변수)의 중요도를 계산해야한다. 중요도는 MDI(Mean Decrease Impurity)를 이용하여 계산한다(MDI에 대한 개념은 여기를 참고하기 바란다). 이 중요도를 이용하여 중요도 Z-score를 계산하게 된다.
아래 그림은 2개의 변수(V1, V2)와 이에 대응하는 2개의 쉐도우 변수(V'1, V'2)를 이용하여 랜덤 포레스트 모형을 학습시킨 뒤 각 변수들의 중요도 Z-score를 계산하는 방법을 나타낸 것이다. 아래 예제에서는 개별 트리 개수를 100으로 선택하였다. 이때 개별 트리에서 각 변수들의 MDI 중요도를 계산한다. 분리 때마다 변수를 랜덤하게 선택하는 랜덤 포레스트의 특성상 개별 트리에서 사용되지 않는 변수가 생길 수 있으므로 이를 '선택' 칼럼에서 X로 표기하고 사용되었다면 O로 표기했다. 이제 각 변수별로 개별 트리에 대하여 중요도 평균과 중요도 표준편차를 계산한다. 그러고 나서 중요도 평균에서 중요도 표준편차를 나눠주면 Z-score가 계산된다.

이제 Z-score가 최대인 쉐도우 변수를 선택하고 이 값보다 큰 Z-Score 값을 갖는 원래 변수에 'Hit'를 체크한다. 즉, 해당 변수가 중요한 변수로 뽑혔다는 것이다. 그리고 원래 변수 중에서 'Hit'가 아닌 것들은 중요하지 않다는 뜻으로 'X' 표시를 해준다.
위 예제에서는 쉐도우 변수 V'2의 Z-score가 가장 크므로 이에 해당하는 값인 2.5와 원래 변수 V1, V2의 Z-score를 비교한다. V1이 2.5보다 크므로 해당 변수에 'Hit' 표시를 하고 2.5보다 작은 V2에 'X' 표시를 한다. 이제 이러한 과정을 반복한다. 왜냐하면 쉐도우 변수를 만드는 데 있어서 랜덤성이 들어가므로 이러한 랜덤성을 보정하기 위해서 반복해야 하기 때문이다. 여기에서는 반복수를 50으로 지정했다고 하자. 그런 다음 각 변수들의 'Hit' 총횟수를 계산한다.

반복이 모두 끝나고 Hit 횟수까지 모두 계산했다. 상식적으로 중요한 변수라면 'Hit' 횟수가 많아야할 것이다. 그렇다면 얼마 이상되어야 많다고 말할 수 있을까? 반대로 중요하지 않은 변수라면 'Hit' 횟수가 적을 것이며 그렇다면 얼마 이하되어야 충분히 적다고 말할 수 있을까?
Boruta는 이항 분포를 이용하여 충분히 많고 적음을 통계적으로 검정한다. 예를 들어 중요한 변수라면 'Hit' 횟수가 랜덤으로 'Hit'를 선택할 확률보다는 클 것이다. 이러한 배경으로 'Hit' 선택 확률을 $p$라 할 때 중요한 변수임을 확인(Confirm)하는 검정은 다음과 같다.
$$H_0 : p=0.5 \;\; \text{vs}\;\; H_a: p>0.5 \tag{1}$$
반대로 중요하지 않은 변수라면 'Hit' 횟수가 랜덤으로 'Hit'를 선택할 확률보다는 작을 것이다. 따라서 중요하지 않다는 것을 판단하기 위해 다음을 검정한다.
$$H_0 : p=0.5 \;\; \text{vs}\;\; H_a: p<0.5 \tag{2}$$
Boruta를 제안한 논문에서는 유의 수준을 0.01로 사용하라고 권고하고 있다. 위 예제에서는 50번 반복했으므로 귀무가설이 참일 때 'Hit' 횟수의 분포는 이항 분포 $B(50, 0.5)$를 따르게 된다. 이를 시각화하면 다음과 같다.
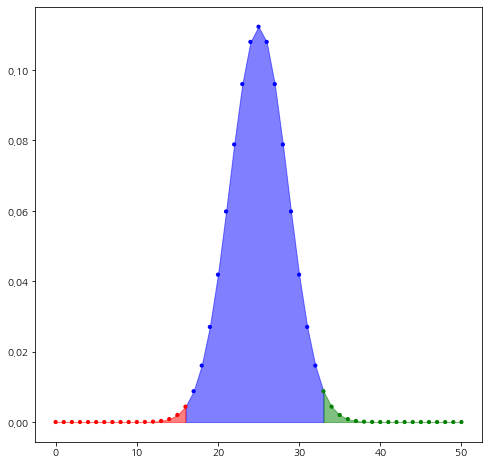
위 그림에서 빨간색 영역은 유의 수준 0.01에서 검정 (2)의 기각역 즉, 중요하지 않다고 결론할 수 있는 영역이고 초록색 영역은 유의 수준 0.01에서 검정 (1)의 기각역 즉, 중요하다고 판단할 수 있는 영역인 것이다. 예제에서 V1의 'Hit' 횟수는 40이고 $X\sim B(50, 0.5)$에 대하여 $P(X\geq 40) = 1.19\cdot 10^{-5}$이므로 위 그림에서 초록색 영역에 포함되고 V1은 중요하다고 판단하게 된다. 마찬가지로 $P(X\leq 12) = 0.0002$이므로 위 그림에서 빨간색 영역에 포함되게 되고 V2는 중요하다고 판단하게 된다.
만약 위 그림에서 파란 영역에 들어간다면 그 변수에 대한 판단은 보류(Tentative)한다.
2) 알고리즘
Boruta 알고리즘은 다음과 같다.
Algorithm
1 단계) 반복수 $m$을 설정한다.
$i=1, \ldots, m$에 대하여 2~8단계)를 반복한다.
2 단계) 원래 변수에 대한 쉐도우 변수 데이터를 만들어준다.
3 단계) 랜덤 포레스트 모형을 학습하고 모든 변수(원래 변수 + 쉐도우 변수)의 중요도의 평균과 표준편차를 계산하고 이를 통해 Z-score를 계산한다.
4 단계) 쉐도우 변수의 Z-score 중에서 가장 큰 값 $z_{\text{max}}$를 계산한다.
5 단계) $z_{\text{max}}$보다 큰 Z-score를 갖는 변수에 'Hit' 표시를 한다.
6 단계) 각 변수별로 'Hit' 총합을 계산하고 검정 (1), (2)를 수행한다. 만약 (2)에서 기각된 변수(중요하지 않은 변수)는 중요하지 않다는 라벨(Rejected)을 달아둔 뒤 다음 스텝부터는 제외시킨다. 만약 (1)에서 기각된 변수(중요한 변수)는 중요하다(Confirmed)는 라벨을 달아둔다(이 녀석은 제외하지 않는다).
7 단계) 기존 쉐도우 변수를 제거한다.
8 단계) 만약 모든 변수들에 대하여 중요하거나 중요하지 않다는 라벨이 모두 달려있다면 종료하고 그렇지 않으면 1 단계)로 돌아간다.
9 단계) $m$번 반복 후에도 라벨이 없는 변수가 있다면 Tentative라는 라벨을 달아준다.
이 알고리즘이 완료되고 나서 'Confirmed' 라벨이 달린 변수들을 최종적으로 선택하게 된다.
3) 알고리즘 고찰
a. Boruta 알고리즘에서 초기 반복 단계
Boruta는 매 반복 시 이항 분포를 이용한 검정 (1), (2)를 수행한다. 이때 반복 초기 단계에서는 충분한 실험 횟수가 아니므로 검정에 대한 신뢰성 문제가 제기될 수 있다.
이를 위해 세 번째 반복 단계까지는 Z-score의 비교를 덜 엄격하게(Less Restrictive)한다고 한다. 원래는 쉐도우 변수 Z-score의 최대값을 기준값으로 설정한다. 하지만 반복 초기에는 많은 변수들이 들어가 있어서 Z-score의 변동성이 발생할 수 있어서 타이트하게 비교하지 않는다고 한다. 예를 들어 첫 번째 반복에서는 내림차순으로 5 번째 Z-score 값, 두 번째 반복에서는 3 번째 Z-score 값, 세 번째 반복에서는 2 번째 Z-score 값을 기준값으로 설정한다고 한다.
Boruta 논문에서는 처음 3번 반복까지는 중요하지 않은 변수를 버리는 검정 (2)만 수행하고 중요한 변수를 선택하는 검정 (1)은 수행하지 않는다고 한다. 중요한 변수를 선택하기 위해서는 최소 4번의 실험이 필요하다고 생각한 것 같다.
b. 랜덤 포레스트의 파라미터 설정
또한 랜덤 포레스트는 randomForest의 기본값을 설정한다고 한다(예 : 트리 개수 500). randomForest의 기본값은 여기를 참고하면 된다. 왜냐하면 이 정도로도 모든 경우에 대해서 적절한 성능을 보여줬기 때문이라고 한다.
3. 장단점
Boruta 변수 선택 알고리즘의 장단점은 다음과 같다.
- 장점 -
a. Boruta는 설명 변수 간 다중 공선성에 덜 민감하다고 한다.
b. 타겟 변수(y)와 복잡한 관계에 있는 설명 변수에 대해서도 중요한 변수를 뽑아낼 수 있다.
랜덤 포레스트(Random Forest) 자체가 설명 변수와 타겟 변수 간 (비선형과 같은) 복잡한 관계를 모델링할 수 있기 때문에 이러한 상황에서도 중요 변수를 추출할 수 있다(cf. LASSO).
- 단점 -
a. 계산 시간이 많이 소요된다.
신뢰성 있는 결과를 얻으려면 랜덤 포레스트를 구성하는 개별 트리의 수가 충분하고 이를 충분히 반복해야 한다. 따라서 정확한 결과를 얻기 위해서 많은 계산 시간이 소요된다.
b. 튜닝 파라미터 선택에 따라 결과가 민감하게 반응할 수 있다.
Boruta는 반복수 또는 유의 수준과 같은 튜닝 파라미터가 있는데 이러한 파라미터들을 신경 써서 값을 정해야 한다.
c. 데이터 품질에 영향을 많이 받는다.
Boruta는 특히 테이터 품질(데이터 개수, 클래스 불균형, 설명 변수의 결측 비율, 관련 없는 변수의 포함 정도 등)에 따라 성능이 좌우된다고 한다.
d. 랜덤 포레스트의 한정되어 있다.
사실 아이디어 자체는 중요도만 계산할 수 있으면 다른 부스팅 모형(Adaptive Boosting, XGBoost 등)에도 적용할 수 있을 것 같기는 하다.
'통계 > 머신러닝' 카테고리의 다른 글
| Bayesian Optimization에 대해서 알아보자! (0) | 2025.10.13 |
|---|---|
| 46. Extremely Randomized Tree(ERT)에 대해서 알아보자. (2) | 2023.05.26 |
| 45. Extended Isolation Forest에 대해서 알아보자. (2) | 2023.05.21 |
| 44. Isolation Forest에 대해서 알아보자. (0) | 2023.05.20 |
| 43. Support Vector Data Description(SVDD)에 대해서 알아보자 with Python (4) | 2023.05.13 |





댓글