이번 포스팅에서는 One-class SVM(1-SVM)과는 다른 방식으로 서포트 벡터 머신 기법을 이용하여 이상치 탐지를 수행하는 Support Vector Data Description(SVDD)에 대해서 알아보고자 한다. 여기서는 Support Vector Data Description(SVDD)의 개념과 파이썬 구현 방법에 대해서 다룬다.
- 목차 -
1. Support Vector Data Description(SVDD)이란 무엇인가?
서포트 벡터 머신(SVM)에 대한 내용을 알면 SVDD를 이해하는 데 도움이 된다. 서포트 벡터 머신에 대한 개념은 아래 포스팅을 참고하면 알 수 있다.
19. 서포트 벡터 머신(Support Vector Machine)에 대해서 알아보자 with Python
19. 서포트 벡터 머신(Support Vector Machine)에 대해서 알아보자 with Python
딥러닝이 나타나기 전에 전성기를 구가했던 서포트 벡터 머신(Support Vector Machine)에 대해서 공부한 내용을 포스팅하려고 한다. 서포트 벡터 머신에 대한 개념과 종류 그리고 파이썬으로 구현하는
zephyrus1111.tistory.com
One-class SVM이 궁금하신 분들은 아래 포스팅을 참고하기 바란다.
41. One-class Support Vector Machine(1-SVM)에 대하여 알아보자 with Python
41. One-class Support Vector Machine(1-SVM)에 대하여 알아보자 with Python
이번 포스팅에서는 모델 기반 이상치 탐지 방법론 중에 하나인 One-class Support Vector Machine(1-SVM)에 대해 알아보고자 한다. 여기에서는 One-class Support Vector Machine(1-SVM)의 개념과 파이썬 구현 방법을
zephyrus1111.tistory.com
1. Support Vector Data Description(SVDD)이란 무엇인가?
1) 정의
Support Vector Data Description(SVDD)은 데이터를 정상과 이상치로 나누는 구(Ball)를 서포트 벡터 머신의 아이디어를 이용하여 찾는 알고리즘이다.
2) 파헤치기
위 정의를 좀 더 살펴보자.
a. SVDD는 데이터를 정상과 이상치로 나누는데 목적이 있다.
SVDD는 One-class SVM과 마찬가지로 라벨이 없는 데이터를 정상과 이상치로 나누는 데 목적이 있다.
b. SVDD는 서포트 벡터 머신의 아이디어를 이용하여 정상치와 이상치를 나누는 구를 찾는다.
SVDD는 정상 데이터를 구(또는 원) 내부에 이상치를 구 바깥에 두어 분리하는 것을 목표로 하며 이러한 구면을 찾는 알고리즘으로써 서포트 벡터 머신의 아이디어를 이용한다. SVDD는 정상을 감싸는 구의 반지름을 최대한 작게 하여 이상치와 최대한 구분시켜 놓는 것을 목표로 한다(아래 그림 참고).
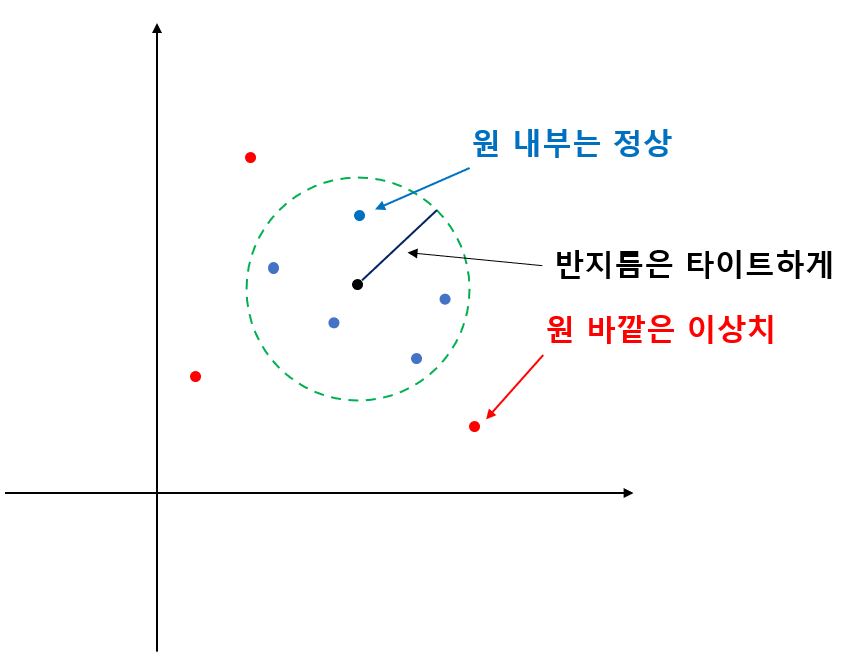
2. SVDD 구면 추정 방법
이제 SVDD에 대한 아이디어를 알았으니 수식을 이용하여 우리가 풀고자하는 문제를 하나씩 정리해 보자.
$l$개의 $p$ 차원 데이터 $x_i$가 있다고 하고 우리가 찾는 구를 중심이 $a (\in \mathbb{R}^p)$ 반지름이 $R$이라고 해보자. 그렇다면 우리가 찾는 구는 다음의 방정식을 만족한다.
$$\| x-a\|_2^2 = R^2 \tag{1} $$
원래는 정상을 (1)의 구 내부에 모두 오도록 해야 하지만 이상치를 허용하기 위해서 슬랙 변수 $\xi_i$를 도입한다. 슬랙 변수는 구의 경계 또는 내부에서는 0, 구 바깥에서는 양수 값을 갖는다.
아래 그림은 데이터가 어떤 조건을 만족하는지 표현한 것이다.
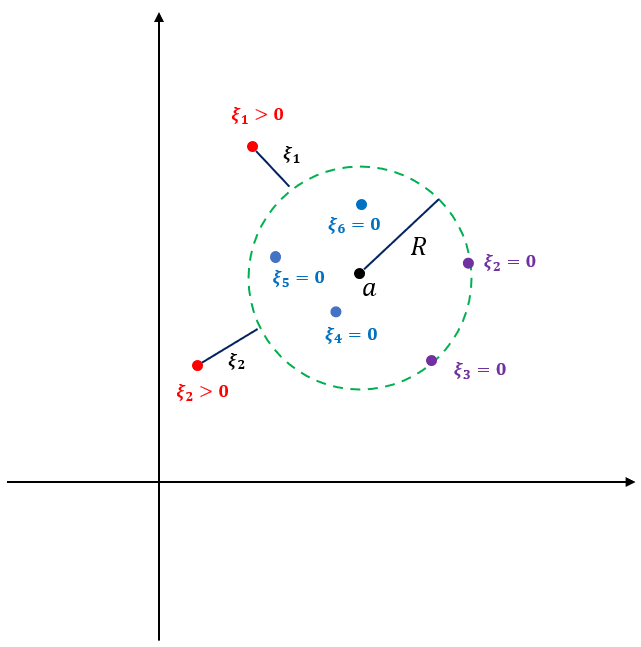
위 그림을 통해서 모든 데이터는 다음을 만족해야 한다.
$$\|x_i -a \|_2^2 \leq R^2 + \xi_i, i=1, \ldots, l \tag{2}$$
이를 정리하면 SVDD는 다음의 최적화 문제를 푸는 것을 알 수 있다.
$$\min_{R \in \mathbb{R}, a \in \mathbb{R}^p, \xi_i \in \mathbb{R}} R^2 + C \sum_{i=1}^l\xi_i \\ \text{subject to}\;\; \|x_i-a \|_2^2 \leq R^2+\xi_i, \xi_i \geq 0, \;\; \forall i=1, \ldots, l \tag{3}$$
여기서 $C>0$이다.
$C$를 크게 하면 작은 $\xi_i$에 대해서도 큰 손실값을 가지므로 $\xi_i$를 최대한 0에 가깝게 다시 말해 이상치를 최대한 안 생기게 하고 반대로 $C$를 작게 하면 이상치를 많이 잡아내게 된다.
이제 (3)을 푸는 방법을 알아보자. 이를 위해 (3)에 대응하는 Lagrangian $L$을 써보면 다음과 같다.
$$\begin{align} L(R, a, \alpha, \gamma, \xi) &= R^2 + C \sum_{i=1}^l\xi_i \\ & -\sum_{i=1}^l\alpha_i \{ R^2+\xi_i-(\| x_i\|_2^2 -2 a\cdot x_i+\|a\|_2^2)\}-\sum_{i=1}^l\gamma_i\xi_i \end{align}\tag{4}$$
여기서 $\alpha_i, \gamma_i \geq 0$이다.
KKT 조건 중 Stationary 조건은 다음과 같다.
(Stationary)
$$\begin{align}\frac{\partial L}{\partial R} &= 2R - 2R\sum_{i=1}^l\alpha_i = 0 \Rightarrow \sum_{i=1}^l\alpha_i=1\tag{S.1} \\ \frac{\partial L}{ \partial a} &= 2\sum_{i=1}^l\alpha_i(x_i - a) = 0 \Rightarrow a = \frac{\sum_{i=1}^l\alpha_ix_i}{\sum_{i=1}^l\alpha_i} = \sum_{i=1}^l\alpha_ix_i \tag{S.2} \\ \frac{\partial L}{\partial \xi_i} &= C-\alpha_i -\gamma_i = 0 \Rightarrow \alpha_i = C-\gamma_i \tag{S.3}\end{align}$$
(S.1)~(S3)을 이용하여 (4)을 다시 쓰면 다음과 같다.
$$L = \sum_{i=1}^l \sum_{j=1}^l \alpha_i\alpha_j x_i^tx_j - \sum_{i=1}^l \alpha_i \| x_i\|_2^2 \tag{5}$$
만약 $x_i$를 Feature Map $\Phi$를 쓴다면
$$L = \sum_{i=1}^l \sum_{j=1}^l \alpha_i\alpha_j \Phi(x_i)^t \Phi(x_j) - \sum_{i=1}^l \alpha_i \|\Phi( x_i) \|_2^2 \tag{6}$$
이 된다. 만약 커널 함수 $k(x_i, x_j) = \Phi(x_i)^t \Phi(x_j)$를 쓴다면
$$L = \sum_{i=1}^l \sum_{j=1}^l \alpha_i\alpha_j k(x_i, x_j) - \sum_{i=1}^l \alpha_i k(x_i, x_i)\tag{7}$$
가 된다. SVDD에서는 보통 다음과 같은 RBF 커널을 사용한다.
$$k(x, y) = \exp \left \{ \frac{1}{s^2} \|x-y \|_2^2 \right \}$$
(3)의 Dual Probloem은 다음과 같아진다.
$$\min_{\alpha \in \mathbb{R}^l} \sum_{i=1}^l \sum_{j=1}^l \alpha_i\alpha_j k(x_i, x_j) - \sum_{i=1}^l \alpha_i k(x_i, x_i) \\ \text{subject to}\;\; 0 \leq \alpha_i \leq C, \sum_{i=1}^l\alpha_i=1 \tag{8} $$
(8)을 풀어서 구한 최적 $\alpha_i$는 다음의 KKT 조건 중 Complementary Slackness를 만족해야 한다.
(Complementary Slackness)
$$\begin{align} \alpha_i \{ R^2+\xi_i-(\| x_i\|_2^2 -2 a\cdot x_i+\|a\|_2^2)\} &= 0 \tag{C.1} \\ \gamma_i\xi_i &= 0 \tag{C.2} \end{align}$$
(S.3)으로부터 $0 \leq \alpha_i \leq C$인 것을 알 수 있다. 이제 $\alpha_i$ 값에 따른 데이터의 범주를 살펴보자.
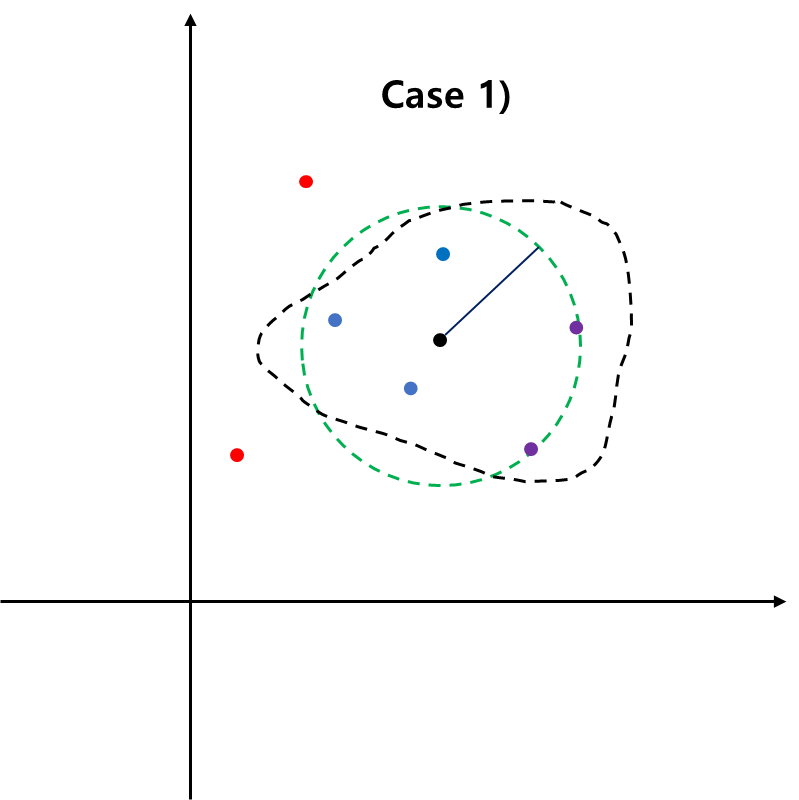
Case 1) $\alpha_i = 0$
$$\begin{align} \alpha_i = 0 & \Rightarrow \gamma_i = C(\neq 0) \;\; \text{∵ (S.3)} \\ & \Rightarrow \xi_i =0 \;\; \text{∵ (C.2)} \end{align}$$
따라서 $\|x_i-a\|_2^2 \leq R$이 된다. 따라서 $\alpha_i=0$에 해당하는 데이터는 구의 경계 또는 구 내부에 있게 된다.
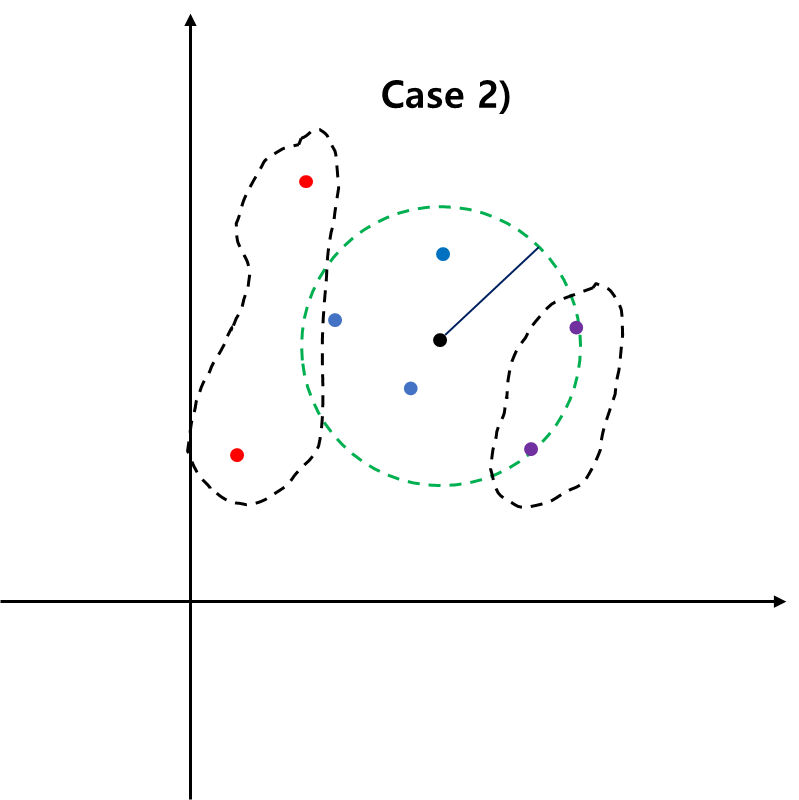
Case 2) $\alpha_i = C$
$\alpha_i = C$이면 (C.1)에 의하여 $\|x_i -a \|_2^2 = R+\xi_i$가 된다. 또한
$$\begin{align} \alpha_i = C &\Rightarrow \gamma_i =0 \;\; \text{∵ (S.3)} \\ & \Rightarrow \xi_i \geq 0 \;\; \text{∵ (C.2)} \end{align}$$
이므로 $\alpha_i = C$에 대응하는 데이터는 구의 경계 또는 구의 바깥쪽에 있게 된다.
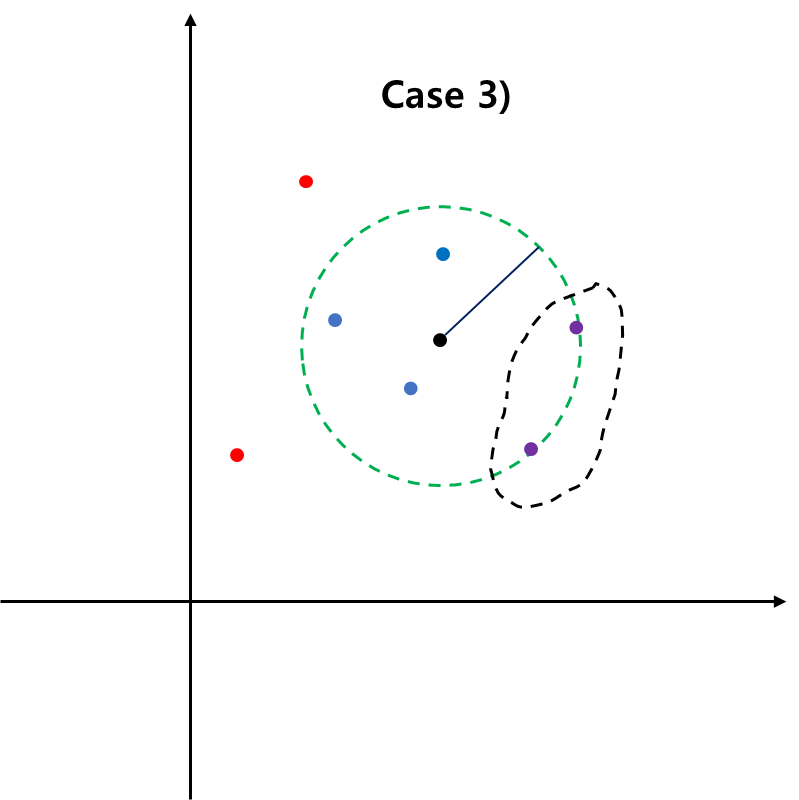
Case 3) $0 < \alpha_i < C$
이 경우 (C.1)에 의하여 $\|x_i -a \|_2^2 = R+\xi_i$가 된다.
$$\begin{align} 0 < \alpha_i < C &\Rightarrow \gamma_i \neq 0 \;\; \text{∵ (S.3)} \\ & \Rightarrow \xi_i = 0 \;\; \text{∵ (C.2)} \end{align}$$
따라서 $\|x_i -a \|_2^2 = R$가 되어 이에 대응하는 데이터는 구의 경계에 있게 된다. 구의 경계에 있는 데이터를 서포트 벡터(Support Vector)라 한다.
(8)을 풀어서 최적 $\alpha_i$를 구했다면 데이터 $z$가 정상인지 아닌지는 다음의 의사결정 함수를 이용하여 결정한다.
$$\begin{align} f(z) &= \text{sign}(R^2-\|z-a \|_2^2) \\ &= \text{sign}\left \{ R^2 - k(z, z) +2\sum_{i=1}^l\alpha_ik(z, x_i)- \sum_{i=1}^l \sum_{j=1}^l \alpha_i\alpha_jk(x_i, x_j) \right \} \end{align} \tag{9}$$
이때 $f(z) = 1$이면 정상 $-1$이면 이상치라고 판단한다.
앞에서 $0<\alpha_i < C$인 경우
$$\begin{align} R^2 = \|x_i-a\|_2^2 \end{align}$$
을 만족한다. 따라서 $R^2$는 다음과 같이 추정한다.
$$\small\begin{align} R^2 &= \frac{1}{|\{ i : 0<\alpha_i < C \}|} \sum_{i : 0<\alpha_i < C}\|x_i-a\|_2^2 \\ &= \frac{1}{|\{ i : 0<\alpha_i < C \}|} \sum_{i : 0<\alpha_i < C} \left \{ k(x_i, x_i) - 2\sum_{j=1}^l\alpha _ik(x_i, x_j) + \sum_{j=1}^l \sum_{m=1}^l \alpha_j\alpha_m k(x_j, x_m) \right \} \end{align} \tag{10}$$
3. 파이썬 구현
이번엔 SVDD를 파이썬으로 구현해 본다. 아래 코드에서 SVDD는 $C$와 RBF 커널 모수 $s$를 받아서 초기화하고 fit 메서드를 통해 정상과 이상치를 나누는 구를 학습한다. 이때 predict 메서드를 통해 주어진 데이터가 정상인지 이상치인지 판별하게 된다.
import numpy as np
from cvxopt import matrix, solvers
class SVDD:
def __init__(self, C=1, s=0.1):
self.C = C ## regularization parameter
self.s = s ## parameter for rbf kernel
self.alpha = None ## alpha
self.R2 = None ## radius
self.Q = None ## kernel matrix
self.X = None
def rbf_kernel(self, x, y, s):
return np.exp(-np.sum(np.square(x-y))/(s**2))
def make_kernel_matrix(self, X, s):
n = X.shape[0]
Q = np.zeros((n,n))
q_list = []
for i in range(n):
for j in range(i, n):
q_list.append(self.rbf_kernel(X[i, ], X[j, ], s))
Q_idx = np.triu_indices(len(Q))
Q[Q_idx] = q_list
Q = Q.T + Q - np.diag(np.diag(Q))
return Q
def fit(self, X):
C = self.C
s = self.s
Q = self.make_kernel_matrix(X, s)
n = X.shape[0]
P = matrix(2*Q)
q = np.array([self.rbf_kernel(x, x, s) for x in X])
q = matrix(q.reshape(-1, 1))
G = matrix(np.vstack([-np.eye(n), np.eye(n)]))
h = matrix(np.hstack([np.zeros(n), np.ones(n)*C]))
A = matrix(np.ones((1, n)))
b = matrix(np.ones(1))
solvers.options['show_progress'] = False
sol = solvers.qp(P, q, G, h, A, b)
alphas = np.array(sol['x'])
rho = 0
alphas = alphas.flatten()
S = ((alphas>1e-3)&(alphas<C))
S_idx = np.where(S)[0]
R2 = alphas.dot(Q.dot(alphas))
for si in S_idx:
temp_vector = np.array([-2*alphas[i]*self.rbf_kernel(X[i, ], X[si, ], s) for i in range(n)])
R2 += (self.rbf_kernel(X[si, ], X[si, ], s) + np.sum(temp_vector))/len(S_idx)
self.R2 = R2
self.alphas = alphas
self.X = X
self.Q = Q
return self
def predict(self, X):
return np.array([np.sign(self._predict(x)) for x in X])
def _predict(self, x):
X = self.X
n = X.shape[0]
alphas = self.alphas
R2 = self.R2
s = self.s
Q = self.Q
first_term = self.rbf_kernel(x, x, s)
second_term = np.sum([2 * alphas[i] * self.rbf_kernel(x, X[i, ], s) for i in range(n)])
thrid_term = alphas.dot(Q.dot(alphas))
return R2-first_term+second_term-thrid_term4. 예제
이제 앞에서 구현한 SVDD 클래스를 테스트해보자. 여기서는 Scikit-Learn(sklearn)에서 시뮬레이션용 데이터를 생성하기 위해 제공된 make_classification을 이용하여 실험용 데이터를 만들어 주었다.
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False
from sklearn.datasets import make_classification
## 실험용 데이터
X, _ = make_classification(n_samples=1000, n_features=2, n_informative=2,
n_redundant=0, n_repeated=0, n_classes=2,
n_clusters_per_class=1,
weights=[0.995, 0.005],
class_sep=0.5, random_state=0)
이제 주어진 데이터를 이용하여 SVDD로 경계면을 학습하고 학습데이터의 정상과 이상치를 판별한 뒤 이를 시각화해 보자.
svdd = SVDD(C=10, s=1).fit(X) ## 경계 학습
labels = svdd.predict(X) ## -1은 이상치, 1은 정상으로 예측하기
fig = plt.figure(figsize=(10, 10))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(X[:, 0], X[:, 1], c=labels)
plt.show()
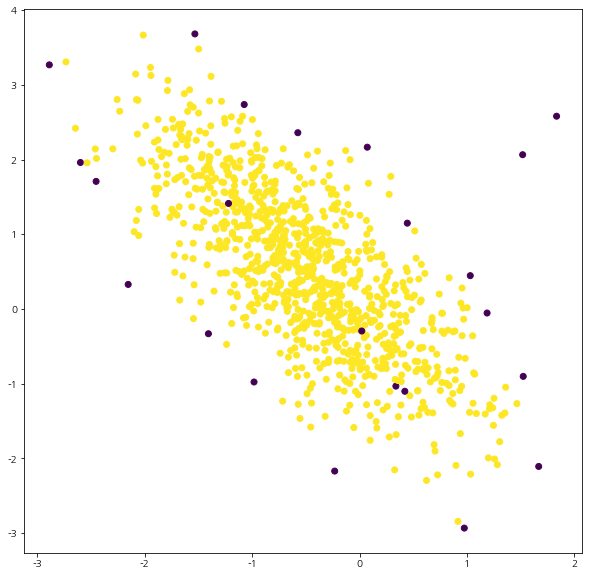
위 그림에서 보라색이 이상치 노란색은 정상으로 간주한 것이다. 이상치로 예측한 것들 중 대부분은 시각적으로 그럴듯해 보이지만 중앙에 (False Alarm) 잘못 예측된 이상치도 껴있는 것을 확인할 수 있었다.
5. 장단점
SVDD의 장단점은 다음과 같다.
- 장점 -
a. 이상치에 민감하지 않다.
애초에 정상 데이터와 많이 떨어진 데이터를 이상치로 판단하고자 하므로 이상치에 민감하지 않다(그냥 이상치라고 예측하면 되니까).
b. 커널을 이용하여 정상과 이상치의 복잡한 비선형 경계면을 표현할 수 있다.
c. $C$를 이용하여 이상치를 얼마나 포함시킬지 결정할 수 있다.
물론 적절한 $C$를 찾기 위해 교차 검증 방법을 사용해야 할 것이다.
- 단점 -
a. SVDD는 커널 함수 $k$의 선택, 커널 파라미터 그리고 정규 파라미터 $C$ 선택에 민감하다.
b. SVDD는 계산 비용이 크다.
큰 데이터에 대해서 계산 비용이 커질 수 있다.
c. 데이터들이 많이 흩어져 있는 경우 SVDD의 성능이 안 좋아질 수 있다.
정상과 이상치의 구분이 무의미할 정도로 (Feature Mapping을 하더라도) 데이터가 흩어져있다면 SVDD를 사용함으로써 얻는 이점이 없을 것이다.
- 참고 자료 -
D.M, Tax, R. P, Duin - Support Vector Data Description
강필성 - 03-6: Anomaly Detection - Auto-Encoder, 1-SVM, & SVDD
'통계 > 머신러닝' 카테고리의 다른 글
| 45. Extended Isolation Forest에 대해서 알아보자. (2) | 2023.05.21 |
|---|---|
| 44. Isolation Forest에 대해서 알아보자. (0) | 2023.05.20 |
| 42. Local Outlier Factor(LOF)에 대해서 알아보자 with Python (0) | 2023.05.13 |
| 41. One-class Support Vector Machine(1-SVM)에 대하여 알아보자 with Python (0) | 2023.05.12 |
| 40. 인자 분석(Factor Analysis)에 대해서 알아보자 with Python (0) | 2023.05.03 |





댓글