이번 포스팅에서는 변수 중요도(Variable Importance)가 무엇인지 알아보고 자주 활용되는 변수 중요도로써 Correlation, Linear Regression Coefficient를 이용한 변수 중요도, Mean Decrease in Impurity(MDI)와 Gini Importance 그리고 Permutation Importance와 Mean Decrease in Accuracy를 소개한다. 또한 파이썬(Python)을 통한 구현 방법도 소개한다.
- 목차 -
2. Correlation, Linear Regression Coefficient
3. Mean Decrease in Impurity(MDI), Gini Importance
4. Permutation Importance, Mean Decrease in Accuracy
1. 변수 중요도란?
a. 정의
변수 중요도는 학습된 모형에 대하여 반응 변수와의 관련성 또는 예측 관점에서 각 변수들의 영향력을 수치화한 것이다.
b. 필요성
1) 인간의 본능
필요성은 너무나도 자명하다. 학습된 모형에 대해서 모든 설명 변수가 반응 변수에 같은 정도로 관련성이 있는 것이 아니기 때문에 어떤 설명 변수($x$)가 반응 변수($y$)에 더 관련성이 있는지 궁금해하는 것은 인간의 본능인 것이다.
2) 머신 러닝 모형의 복잡성
최근 머신 러닝(또는 딥러닝) 지도 학습 분야에서 예측 모형은 예측력이 좋아지는 대신 모형이 굉장히 복잡해졌다. 모형이 복잡해졌다고 함은 1) 주어진 입력값과 그에 대한 예측값의 관계를 선형 회귀 모형처럼 쉽게 파악하기 어렵고 2) 모형 자체에 대한 해석을 의사결정나무처럼 쉽게 할 수 없음을 의미한다.
이 말은 곧 어떤 변수가 예측과 관련되어 중요한 변수인지를 파악하기 어렵다는 뜻이 된다.
따라서 모형의 예측력과 관련하여 개별 변수의 영향력을 측정하는 도구의 필요성이 나타나게 되었다.
2. Correlation, Linear Regression Coefficient
먼저 가장 나이브하게 생각해볼 수 있는 변수 중요도를 생각해보자. 바로 상관 계수(Correlation)와 선형 회귀 모형의 회귀 계수(Regression)이다.
a. 아이디어
먼저 데이터 $(x_i, y_i), i=1, \ldots, n$가 있다고 하자. $x_i=(x_{i1}, \ldots , x_{ip})^t$는 $p$차원 설명 변수 벡터이고 반응 변수 $y_i$는 실수 또는 범주를 나타내는 숫자라고 하자.
1) Correlation
중요한 설명 변수라면 해당 변수는 반응 변수와의 상관관계가 크다는 아이디어에 착안하여 Correlation을 변수 중요도로 생각하게 된 것이다. 하지만 상관 계수는 -1과 1 사이 즉, 음수값과 양수값을 가질 수 있기 때문에 그 자체로 변수 중요도로 쓸 수 없고 상관 계수의 절대값을 변수 중요도로 쓴다. 이렇게 되면 0과 1 사이의 값을 가지기 때문에 각 변수별로 중요도를 비교할 수 있다.
2) Linear Regression Coefficent(LRC)
Correlation은 각 변수와 반응 변수의 직접적인 관계를 이용한 변수 중요도인 반면 Linear Regression Coefficient(LRC)는 주어진 설명 변수를 모형에 집어넣고 개별 회귀 계수의 절대값이 클수록 해당 설명 변수가 반응 변수 예측값에 더 많은 영향력을 행사한다는 점에 착안하여 만들어진 변수 중요도이다.
b. 알고리즘
1) Correlation
Correlation을 통한 $j$번째 설명 변수의 중요도 $I_j$는 다음과 같이 계산한다.
Algorithm 1
$j = 1, \ldots, p$에 대하여
$$I_j = \left | \frac{\sum_{i=1}^n(x_{ij}-\bar{x}_j)(y_i-\bar{y})}{\sqrt{\sum_{i=1}^n(x_{ij}-\bar{x}_j )^2} \sqrt{ \sum_{i=1}^n(y_i -\bar{y})^2 } } \right |$$
여기서 $\bar{x}_j = \sum_{i=1}^nx_{ij}/n, \bar{y} = \sum_{i=1}^ny_i/n$ 이다.
2) Linear Regression Coefficent(LRC)
LRC를 통한 $j$번째 설명 변수의 중요도 $I_j$는 다음과 같이 계산한다.
Algorithm 2
단계 1)
선형 회귀 모형 $f$을 적합한다. 이때 설명 변수는 각 변수의 표본표준편차로 나눠준다. 이는 스케일에 상관없이 회귀 계수를 비교하고자 함이다.
$$\hat{y}=f(x)=b_0+b_1x_1+\ldots+b_px_p$$
단계 2)
$j = 1, \ldots, p$에 대하여
$$I_j = \frac{|b_j|}{\sum_{k=1}^p|b_k|}$$
c. 예제
여기서는 두 개의 참(True) 모형을 가정하고 이 모형에서 샘플링된 데이터를 이용하여 변수 중요도를 뽑고자 한다. 여기서 고려한 모형은 다음과 같다.
$$\begin{align} \text{Model 1} & \;\;y_{i1} = 0.5\cdot x_{i1}+0.02 \cdot x_{i3}+0.9 \cdot x_{i4} + 0.01\cdot e_{i1} \\ \text{Model 2} & \;\; y_{i2} = 0.5\cdot x_{i1}+0.02 \cdot x_{i3}+0.9 \cdot x_{i4} \\ & +0.9 \cdot x_{i1}\cdot x_{i5} - 0.9 \cdot x_{i1}\cdot x_{i4}+0.01*e_{i2}, \; i=1, 2, \ldots, 100 \end{align}$$
이때 $x_{i1}, x_{i2}, x_{i3} \sim U(0, 1), x_{i4}, x_{i5}, e_{i1}, e_{i2} \sim N(0, 1)$이다.
Model 1은 $x_1, x_3, x_4$의 주 효과(Main Effect)로 이루어진 선형 모형이며 Model 2는 Model 1에서 교호항(Interaction Term)을 추가한 것이다.
Model 1을 보면 $x_4, x_1, x_3$의 순으로 $y_1$과 관련성이 강한 것을 직관적으로 알 수 있다. 이번 실험을 통해 Correlation과 LRC를 이용한 변수 중요도를 계산하고 그 순서가 $x_4, x_1, x_3$ 순서로 나오는지 확인해본다. Model 2를 고려한 이유는 기존 Model 1에서 교호항이 있는 경우 이를 무시한 채 변수 중요도를 계산하면 주 효과(Main Effect) 영향력 순위 $x_4, x_1, x_3$를 제대로 식별할 수 있는지 살펴보기 위함이다.
실제 모형이 위와 같이 주어진 경우 $x_1, \ldots, x_5$의 변수 중요도를 구해보자. 먼저 실제 모형 2개에 대해서 데이터 샘플을 만들어준다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
np.random.seed(100)
sample_size = 100
x1 = np.random.rand(sample_size)
x2 = np.random.rand(sample_size)
x3 = np.random.rand(sample_size)
x4 = np.random.randn(sample_size)
x5 = np.random.randn(sample_size)
error1 = np.random.randn(sample_size)
error2 = np.random.randn(sample_size)
y1 = 0.5*x1+0.02*x3+0.9*x4+0.01*error1
y2 = 0.5*x1+0.02*x3+0.9*x4+0.9*x1*x5-0.9*x1*x4+0.01*error2
그리고 Correlation과 LRC을 통한 변수 중요도를 계산하는 함수와 이를 시각화해주는 함수를 만들어준다.
def correlation(X, y):
res = [np.abs(np.corrcoef(X[:,i], y)[1,0]) for i in range(5)]
return res
def LRC(X, y):
std = np.std(X, axis=0)
std_X = X/std
reg = LinearRegression().fit(X, y)
coef_sum = np.sum(np.abs(reg.coef_))
res = np.abs(reg.coef_)/coef_sum
return res
def plot_importance(X, y, importance):
temp1 = ['x1', 'x2', 'x3', 'x4', 'x5']
temp2 = importance(X, y)
result = sorted(zip(temp1, temp2), key=lambda x:x[1])
label = [x[0] for x in result]
value = [x[1] for x in result]
fig = plt.figure(figsize=(6,7))
fig.set_facecolor('white')
plt.barh(label, value, height=0.5)
plt.show()
1) Correlation
먼저 첫 번째 모형에서 나온 반응 변수 $y_1$과 각 설명 변수의 중요도를 시각화해보자.
plot_importance(X, y1, correlation)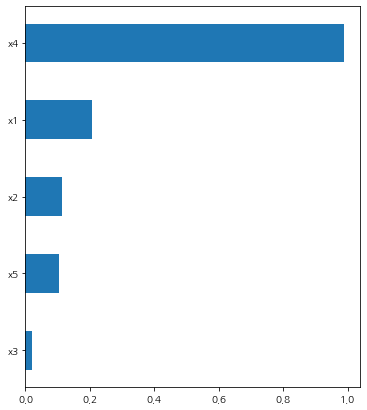
보는 바와 같이 $x_4, x_1$의 변수 중요도가 높게 나왔다. 이는 Model 1에서 예상한 변수 중요도와 순위를 얼추 맞추었다. 하지만 $x_3$은 실제로 Model 1과 관련이 있음에도 불구하고 아무 관련이 없는 $x_2, x_3$ 보다 변수 중요도가 오히려 더 낮게 나왔다.
다음으로 두 번째 모형에서 나온 반응 변수 $y_2$와 각 설명 변수의 중요도를 시각화해보자.
plot_importance(X, y2, correlation)
여기서는 $x_5$가 실제로는 Model 2에서 주 효과가 없음에도 불구하고 가장 큰 변수 중요도를 나타내었다. 교호 작용이 존재하는 경우 상관 계수는 주 효과에 대한 중요 변수를 뽑아내는 능력이 한계가 있다고 추측할 수 있다.
2) Linear Regression Coefficent(LRC)
이번엔 LRC를 통한 변수 중요도를 뽑아보자. 먼저 Model 1에 대한 변수 중요도를 살펴보자.
plot_importance(X, y1, LRC)

보는 바와 같이 LRC를 통한 변수 중요도는 Model 1의 회귀 계수 절대값 순서와 정확하게 일치하였다. 또한 $x_2, x_5$는 Correlation에서는 0보다 어느 정도 크게 나왔는데 LRC를 이용한 변수 중요도에서는 거의 0에 가까운 값을 보여서 중요한 변수들을 정확하게 식별해냈다.
다음으로 Model 2에 대한 변수 중요도이다.
plot_importance(X, y2, LRC)

Correlation과 마찬가지로 $x_5$의 변수 중요도가 가장 크게 나왔다. LRC의 경우에도 교호 작용이 존재하는 경우 주 효과에 대한 중요 변수를 뽑아내는 능력이 약하다고 추측할 수 있다.
d. 장단점
1) Correlation
- 장점 -
a. 구현이 쉽다.
Correlation을 이용한 변수 중요도는 상관 계수만 구하면 되므로 구현이 너무 쉽다.
b. 직관적이다.
반응 변수와의 직접적인 상관 정도를 보는 것으로 직관적이다.
c. 설명 변수 단위에 영향을 받지 않는다.
d. 특별한 예측 모형 학습 과정이 필요치 않다.
- 단점 -
a. 여러 설명 변수에 대한 영향력이 동시에 존재하는 경우 실제로 중요한 변수가 관계없는 변수보다 오히려 중요도가 낮게 나올 수 있다.
b. 교호 작용에 영향을 받는다.
반응 변수에 두 변수간 교호 작용이 있는 경우 Correlation은 주 효과(Main Effect)에 대한 중요도를 제대로 식별하지 못할 수 있다.
c. 범주형 반응 변수에 적용이 어렵다.
Correlation는 기본적으로 연속형 변수들을 가정한다. 따라서 반응 변수가 범주형인 경우 Correlation을 변수 중요도로 사용하기에는 부적절하다.
d. 이상치에 민감하다.
2) Linear Regression Coefficent(LRC)
- 장점 -
a. 구현이 쉽다.
LRC를 이용한 변수 중요도는 구현이 너무 쉽다.
b. 직관적이다.
반응 변수와에 영향을 끼치는 정도를 나타내는 회귀 계수를 사용하므로 직관적이다.
c. 주 효과에 대한 중요 변수를 LRC를 통해 정확하게 잡아낼 수 있다.
설명 변수의 주 효과(1차 항)로 이루어진 모형에 대해서 관계없는(독립인) 변수들은 발라내고 모형 속에 포함된 주 효과를 그 순서까지 정확하게 잡아낼 수 있다.
d. 특별한 검증 데이터가 필요 없다.
LRC는 선형 모형 학습 과정에서 얻어지는 것이므로 특별한 검증 데이터가 필요치 않다.
- 단점 -
a. 교호 작용에 영향을 받는다.
반응 변수에 두 변수간 교호 작용이 있는 경우 LRC는 Correlation과 마찬가지로 주 효과(Main Effect)에 대한 중요도를 제대로 식별하지 못할 수 있다.
b. 단위에 영향을 받으므로 표준화를 통한 전처리를 해줘야 한다.
c. 범주형 반응 변수에 적용이 어렵다.
LRC는 기본적으로 연속형 반응 변수를 취급한다. 따라서 반응 변수가 범주형인 경우 LRC를 변수 중요도로 사용하기에는 부적절하다. 이때에는 대안으로 로지스틱 회귀 계수를 사용할 수도 있을 것이다.
d. 이상치에 민감하다.
e. 실제 모형이 선형과 가깝지 않은 경우에는 쓰기 어렵다.
3. Mean Decrease in Impurity(MDI), Gini Importance
Mean Decrease in Impurity(MDI)는 랜덤 포레스트(기본 학습기(Base Learner)가 의사결정나무인 배깅 모형)에서 개별 나무의 불순도(Impurity)의 변화량을 이용하여 변수 중요도를 계산하는 방법이다. 이때 불순도 측도가 지니 계수(Gini Index)인 경우의 변수 중요도를 Gini Importance(GI)라고 한다. 물론 랜덤 포레스트가 아닌 단독(Single) 의사결정나무에 대해서도 적용할 수 있다.
a. 아이디어
먼저 데이터 $(x_i, y_i), i=1, \ldots, n$가 있다고 하자. $x_i=(x_{i1}, \ldots , x_{ip})^t$는 $p$차원 설명 변수 벡터이고 반응 변수 $y_i$는 실수 또는 범주를 나타내는 숫자라고 하자.
MDI의 아이디어는 간단하다. 개별 나무에 대해서 불순도 감소분이 큰 변수가 중요하다는 아이디어에서 고안된 것이 MDI이다.
b. 알고리즘
MDI를 이용한 변수 중요도는 다음과 같은 알고리즘을 통해 계산된다.
Algorithm 3
학습된 랜덤 포레스트 모형이 주어졌을 때 개별 나무의 개수 $M$, 개별 나무 특정 노드(또는 마디) $R$에서의 불순도를 $\text{Imp}(R)$이라 하자.
$j=1, \ldots, p$에 대해서 다음 과정을 반복한다.
단계 1)
$m = 1, \ldots, M$에 대하여 개별 나무를 $t_m$라 할 때 다음과 같이 $I_{jm}$을 계산한다.
$$I_{jm} = \sum_{R : j \in R \in t_m} \left [ \frac{n_R}{n} \text{Imp}(R) - \frac{n_{R_\text{left}}}{n} \text{Imp}(R_\text{left}) - \frac{n_{R_\text{right}}}{n} \text{Imp}(R_\text{right}) \right ] $$
여기서 $n_R$은 노드 $R$에서의 샘플 수, $\{R : j \in R \in t_m \}$은 개별 나무 $t_m$에서 분리할 때 $j$번째 변수를 선택한 노드들의 집합을 의미한다. 또한 $R_\text{left}, R_\text{right}$는 각각 노드 $R$의 왼쪽 노드와 오른쪽 노드를 의미한다.
단계 2)
$j$ 번째 변수에 대한 중요도 $I_j$를 다음과 같이 계산한다.
$$I_j = \frac{1}{M}\sum_{m=1}^MI_{jm}$$
정규화(Normalization)을 한다면 다음과 같이 변환한다.
$$I_j' = \frac{I_j}{\sum_k I_k}$$
c. 예제
1) 예제로 알아보는 MDI
예제를 통해 MDI(Mean Decrease in Impurity) 계산 방법을 알아보자. 여기서는 설명의 편의를 위하여 하나의 의사결정나무(Decision Tree)가 있다고 가정해보겠다. 학습된 의사결정나무가 다음과 같다.
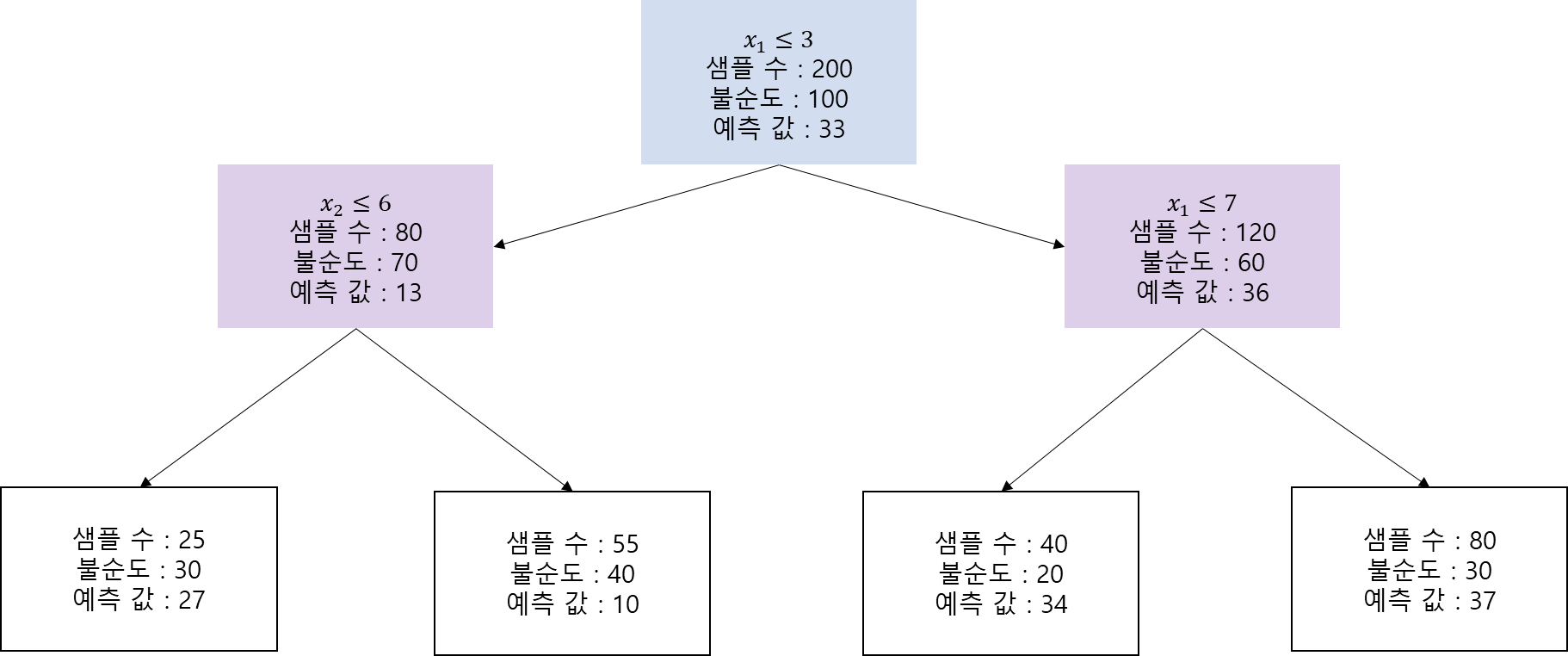
이제 MDI 기반 $x_1$의 변수 중요도 $I_1$을 계산한다. 먼저 뿌리 마디(Root Node)에서 $x_1$이 사용되었으므로 해당 노드와 자식 노드들 사이의 불순도(Impurity) 감소분을 계산해야 한다. 여기서 불순도는 지니 계수, 엔트로피, 평균 잔차 제곱(MSE) 등이 될 수 있다.
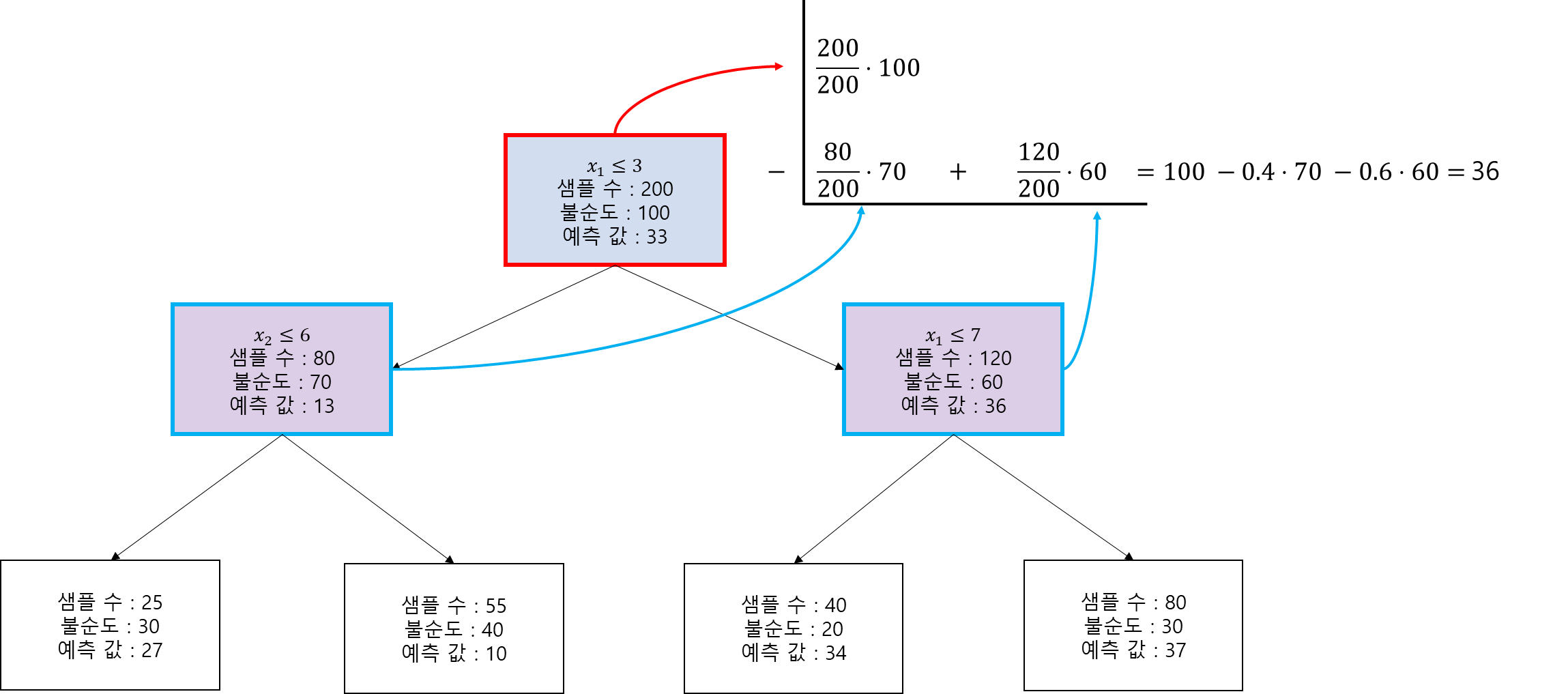
뿌리 마디 $R_0$에서의 $x_1$의 불순도 감소분은 36이다. 그리고 뿌리 마디의 오른쪽 자식 노드에서도 $x_1$이 사용되었으므로 해당 노드의 불순도 감소분을 계산해야 한다.
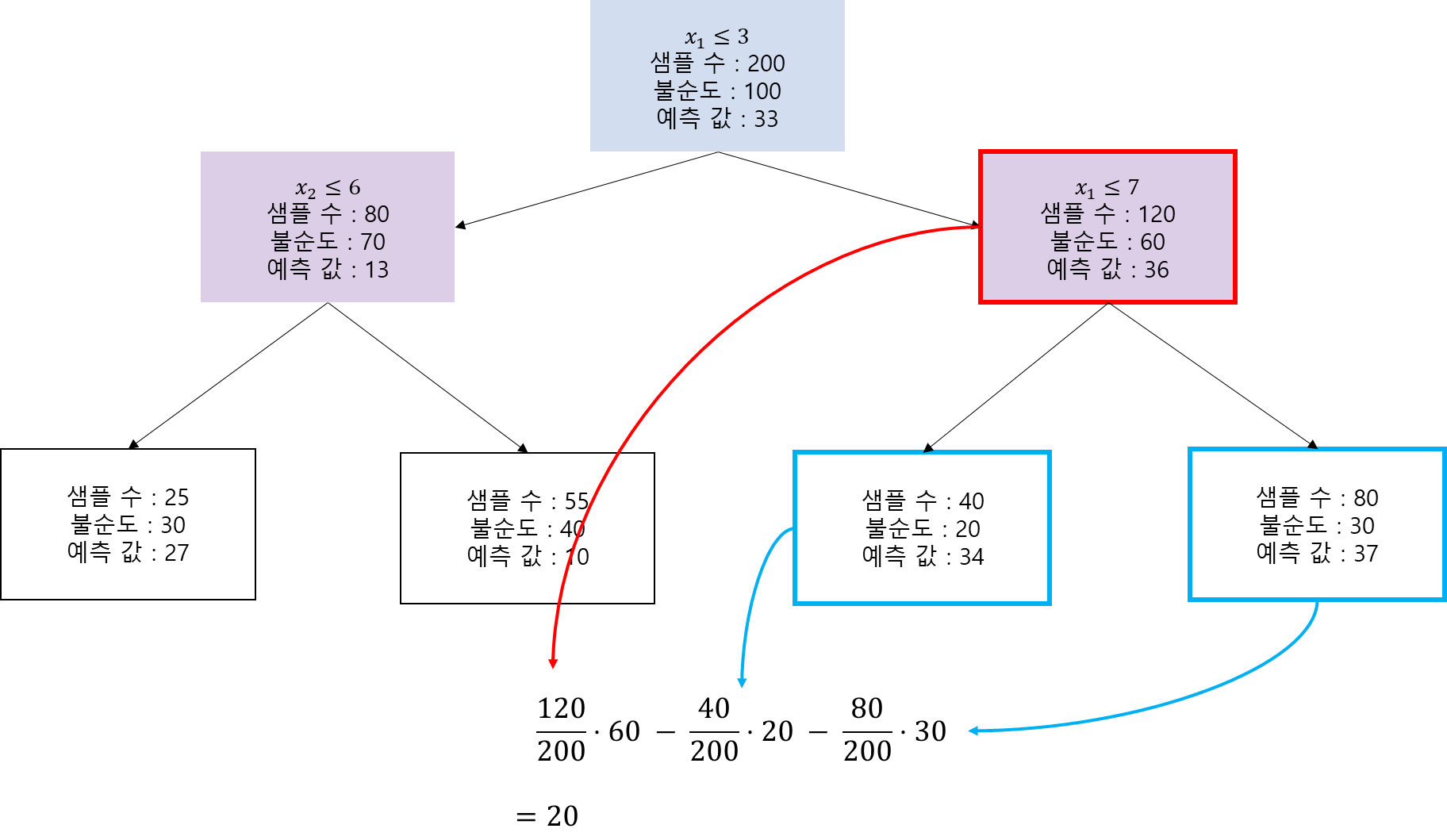
오른쪽 자식 노드(빨간 박스) $R_1$에서의 불순도 감소분은 20이다. 따라서
$$I_j = I_{1, 0} + I_{1, 1} = 36+20 = 56$$
이 된다. 연습 삼아 $x_2$의 MDI 기반 변수 중요도를 계산해보기 바란다.
랜덤 포레스트에서는 개별 나무에 대해서 중요도를 계산하고 평균을 취해줘야 한다.
2) 파이썬 (Python) 구현
이번엔 파이썬(Python)으로 MDI(Mean Decrease in Impurity) 기반 변수 중요도를 계산하는 함수를 구현해보고자 한다.
아래 코드는 MDI 변수 중요도를 계산하는 feature_importance 함수이다. 이 함수는 학습된 model을 인자로 받으며 내부에는 각 노드별 불순도 감소분을 계산하는 node_importance가 있다. 이 함수는 노드 번호(node), 변수(feature), feature_imp_val을 받는다.
이때 해당 노드의 분리 변수가 feature와 일치하면 불순도 감소 분을 계산한다. 그리고 해당 노드의 자식 노드 하나라도 터미널 노드(Terminal Node, Leaf Node)라면 함수를 종료한다(7~22).
def feature_importance(model):
num_feature = model.tree_.n_features ## 피처 개수
def node_importance(node, feature, feature_imp_val):
left_child = model.tree_.children_left[node]
right_child = model.tree_.children_right[node]
if feature == model.tree_.feature[node]:
total_samples = model.tree_.n_node_samples[0]
w = model.tree_.n_node_samples[node]
w_left = model.tree_.n_node_samples[left_child]
w_right = model.tree_.n_node_samples[right_child]
parent_impurity = model.tree_.impurity[node]
left_impurity = model.tree_.impurity[left_child]
right_impurity = model.tree_.impurity[right_child]
feature_imp_val = (w*parent_impurity-w_left*left_impurity-w_right*right_impurity)/total_samples
if left_child == right_child: ## 끝마디
return feature_imp_val
if left_child == -1:
return feature_imp_val+node_importance(right_child, feature, 0)
if right_child == -1:
return feature_imp_val+node_importance(left_child, feature, 0)
return feature_imp_val+node_importance(left_child, feature, 0)+node_importance(right_child, feature, 0)
fi = np.array([node_importance(0, i, 0) for i in range(num_feature)])
total_sum_fi = np.sum(fi)
normalized_fi = fi/total_sum_fi ## 정규화
return normalized_fi
코드로 구현했으니까 테스트해보는 게 인지상정이다. 보스턴 집값 데이터를 이용하여 모형을 학습하고 MDI 변수 중요도를 계산해보자.
먼저 의사결정 나무로 학습했다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
## 보스턴 데이터
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['MEDV'] = boston.target
X = df[['AGE', 'RAD', 'TAX', 'DIS', 'RM', 'LSTAT', 'B', 'INDUS', 'CHAS']].values
y = df['MEDV'].values
## 예측 모형 모형 적합
model = DecisionTreeRegressor(max_depth=4, random_state=0).fit(X, y)
이제 DecistionTreeRegressor 클래스 내부의 변수 중요도와 내가 구현한 변수 중요도를 비교해보자.
print('SKlearn :', model.feature_importances_)
print('구현한거 :', feature_importance(model))

정확하게 일치했다~!! 이번엔 랜덤 포레스트로 적합해보고 변수 중요도를 뽑아 보자.
## 예측 모형 모형 적합
model = RandomForestRegressor(max_depth=4, random_state=0, n_estimators=10).fit(X, y)
print('SKlearn :', model.feature_importances_)
print('구현한거 :', np.mean([feature_importance(est) for est in model.estimators_], axis=0))

약간의 차이가 있다. 혹시 중요도 랭킹은 서로 다른지 살펴보고 싶어서 시각화를 해보았다.
def plot_importance(importance, ax, x_label):
temp1 = [f'x{i}' for i in range(len(importance))]
temp2 = importance
result = sorted(zip(temp1, temp2), key=lambda x:x[1])
label = [x[0] for x in result]
value = [x[1] for x in result]
ax.barh(label, value, height=0.5)
ax.set_xlabel(x_label)
ax.set_ylabel('Importance')
fig, axs = plt.subplots(1, 2)
fig.set_facecolor('white')
fig.set_figwidth(12)
fig.set_figheight(7)
ax1 = plt.subplot(1, 2, 1)
ax2 = plt.subplot(1, 2, 2)
plot_importance(model.feature_importances_, ax1, 'sklearn')
my_importance = np.mean([feature_importance(est) for est in model.estimators_], axis=0)
plot_importance(my_importance, ax2, 'my importance')
plt.show()
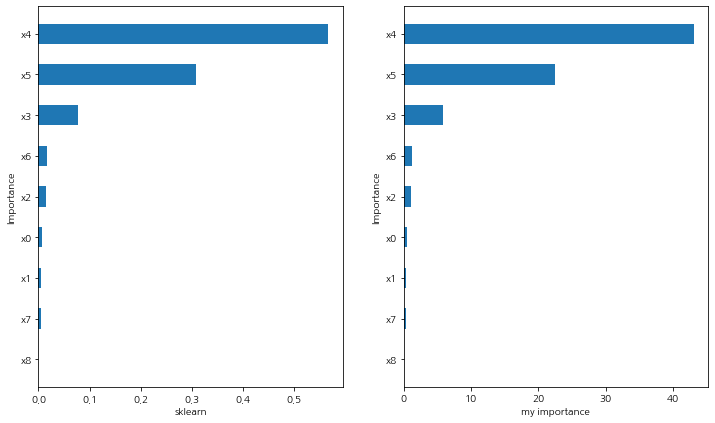
다행히도 중요도 둘 다 같았다. 중요도는
$$x_4 > x_5 > x_3 > x_6 > x_2 > x_0 > x_1 > x_7 > x_8 $$
으로 높았으며 $x_4$가 이 나무를 형성하는 데 있어서 가장 큰 영향력을 행사하였다.
변수 중요도 값이 차이가 나는 이유를 조사해보았다. 개별 나무 하나 선정해서 중요도를 계산해보니 내가 구현한 것이 계산적으로 맞았다. 이번엔 Scikit-Learn 코드를 살펴보았는데 내 머리로는 잘 모르겠다.
d. 장단점
- 장점 -
a. 반응 변수가 연속형 범주형 모두 다룰 수 있다.
b. 설명 변수 이상치에 덜 민감하다.
c. 별도의 검증 데이터가 필요 없다.
MDI는 모형을 적합하는 과정에서 계산되므로 검증 데이터가 필요 없는 변수 중요도 계산 방법이다.
- 단점 -
a. 의사결정나무만 적용할 수 있는 방법이다.
소위 모형 클래스에 상관없는(Model-Agnostic) 방법이 아니다.
b. 일반화되기 어렵다.
별도의 테스트 데이터 없이 학습된 모형을 기반으로 계산된 변수 중요도라서 새로운 데이터에 대해서도 같은 중요도를 갖는다고 말하기 어렵다.
c. 유니크한 값이 많은 설명 변수가 포함되어 있다면 해당 변수에 대해서 과도하게 중요하다는 결과를 얻을 수 있다. 범주형같이 적은 것은 실제로 중요하더라도 유니크한 값이 많은 변수를 이길 수 없다.
4. Permutation Importance, Mean Decrease in Accuracy
Permutation Importance는 예측하고자 할 데이터 셋(보통 테스트 데이터 셋)의 각 변수를 재 배열(Permutation) 한 후의 예측력이 얼마나 변하는지 알려주는 변수 중요도이다. 이때 Permutation Importance 방식을 랜덤 포레스트에 적용한 것이 Mean Decrease in Accuracy(MDA)이다.
a. 아이디어
Permutation Importance의 아이디어는 (테스트 데이터 내) 특정 변수가 예측력에 영향을 미치지 않는다면 특정 변수를 재배열하더라도 예측력이 크게 달라지지 않을 것이라는 아이디어에서 고안되었다.

반대로 특정 변수를 재배열했을 때의 예측력이 기존 예측력과 비교하여 매우 달라졌다면 해당 변수는 예측력에 영향을 크게 작용한 것으로 생각할 수 있는 것이다.
b. 알고리즘
Algorithm 4
먼저 학습된 예측 모형 $f$, 변수 중요도를 계산할 데이터 셋 $D$, 반복수 $T$가 있다고 하자.
이때 $j = 1, 2, \ldots, p$에 대하여 다음을 반복한다.
단계 1)
먼저 $D$를 이용하여 $f$의 예측력(정확도, 평균잔차제곱 등) $s$를 계산한다.
단계 2)
$t = 1, 2, \ldots, T$에 대하여
$D$에서 $j$ 번째 변수(칼럼)만 재배열(Random Shuffling, Permutation)을 시킨다. 재배열시킨 데이터를 $\tilde{D}_{t, j}$라 하자.
이때 예측 모형 $\tilde{D}_{t, j}$를 이용하여 $f$의 예측력(정확도, 평균잔차제곱 등) $s_{t, j}$을 계산한다.
단계 3)
$j$번째 변수 중요도 $I_j$를 다음과 같이 계산한다.
$$I_j = s - \frac{1}{T}\sum_{t=1}^Ts_{t, j}$$
추가적으로 MDA를 이용한 변수 중요도 알고리즘도 소개한다.
Algorithm 5
학습된 랜덤 포레스트 모형 $f$, 변수 중요도를 계산할 데이터 셋 $D$, 반복수 $T$가 있다고 하자. 그리고 랜덤 포레스트의 개별 나무 개수는 $M$이다.
이때 $j = 1, 2, \ldots, p$에 대하여 다음을 반복한다.
$m = 1, 2, \ldots, M$에 대하여
→ $m$번째 나무 $t_m$의 OOB(Out of Bag) 데이터를 $O_m$이라 하자. 이때 $t_m$에 대한 $O_m$의 예측력 $s_m$을 계산한다.
→ $t = 1, 2, \ldots, T$에 대하여
$O_m$에서 $j$ 번째 변수(칼럼)만 재배열(Random Shuffling, Permutation)을 시킨다. 재배열시킨 데이터를 $\tilde{O}_{m, t, j}$라 하자
이때 예측 모형 $\tilde{O}_{m, t, j}$를 이용하여 $t_m$의 예측력 $s_{m, t, j}$을 계산한다.
→ $t_m$의 $j$번째 변수의 중요도 $I_{m, j}$를 다음과 같이 계산한다.
$$I_{m, j} = s_m - \frac{1}{T}\sum_{t=1}^Ts_{m, t, j}$$
이제 $j$번째 변수 중요도 $I_j$를 다음과 같이 계산한다.
$$I_j = \frac{1}{M}\sum_{m=1}^MI_{m, j}$$
c. 예제
Permutation Importance를 파이썬(Python)으로 구현해보자.
아래 코드는 Permutation Importance를 수행하는 함수이다. 이 함수는 학습 모델(model), 변수 중요도 계산에 사용할 X, y 데이터(X_data, y_data), 재배열 반복 횟수(repetition), seed 숫자(random_state)를 인자로 받는다. 이 함수는 각 변수 중요도와 변수 중요도의 표준편차를 리턴하도록 했다.
def permutation_importance(model, X_data, y_data, repetition=30, random_state=100):
np.random.seed(random_state)
num_features = model.n_features_ ## 총 변수 개수
score = model.score(X_data, y_data)
importance = []
importance_std = []
for j in range(num_features):
perm_data = X_data.copy()
score_tj = []
for t in range(repetition):
permuted_j = np.random.permutation(perm_data[:, j])
perm_data[:, j] = permuted_j
score_tj.append(model.score(perm_data, y_data))
importance.append(score-np.mean(score_tj))
importance_std.append(np.std(score_tj))
importance = np.array(importance)
importance_std = np.array(importance_std)
return importance, importance_std
이번에도 데이터는 보스턴 집값 데이터, 모델은 의사결정나무를 사용했다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import load_boston
from sklearn.tree import DecisionTreeRegressor
from sklearn.inspection import permutation_importance
## 보스턴 데이터
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['MEDV'] = boston.target
X = df[['AGE', 'RAD', 'TAX', 'DIS', 'RM', 'LSTAT', 'B', 'INDUS', 'CHAS']].values
y = df['MEDV'].values
## 예측 모형 모형 적합
model = DecisionTreeRegressor(max_depth=4, random_state=0).fit(X, y)
이제 변수 중요도와 표준편차를 계산하고 출력해보자. 이때 데이터는 학습 데이터를 사용했다.
X_data = X
y_data = y
importance, importance_std = permutation_importance(model, X_data, y_data, repetition=30, random_state=100)
for i, res in enumerate(zip(importance, importance_std)):
print(f'x{i} :', f'{res[0]:.3f}', '+/-', f'{res[1]:.3f}')
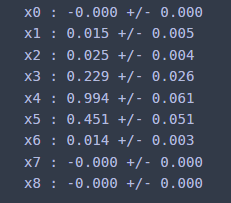
이번엔 sklearn에서 제공하는 Permutation Importance 결과와 일치하는지 확인해보았다.
r = permutation_importance(model, X_data, y_data,
n_repeats=30,
random_state=0)
for i, res in enumerate(zip(r.importances_mean, r.importances_std)):
print(f'x{i} :', f'{res[0]:.3f}', '+/-', f'{res[1]:.3f}')

값의 차이는 있으나 중요도 랭킹은 같았다. 시각화 결과로도 확인해보자.
def plot_importance(importance, importance_std, ax, x_label):
temp1 = [f'x{i}' for i in range(len(importance))]
temp2 = importance
temp3 = importance_std
result = sorted(zip(temp1, temp2, temp3), key=lambda x:x[1])
label = [x[0] for x in result]
value = [x[1] for x in result]
value_2 = [x[2] for x in result]
ax.barh(label, value, xerr=value_2, height=0.5)
ax.set_xlabel(x_label)
ax.set_ylabel('Importance')
fig, axs = plt.subplots(1, 2)
fig.set_facecolor('white')
fig.set_figwidth(12)
fig.set_figheight(7)
ax1 = plt.subplot(1, 2, 1)
ax2 = plt.subplot(1, 2, 2)
plot_importance(r.importances_mean, r.importances_std, ax1, 'sklearn')
plot_importance(importance, importance_std, ax2, 'my importance')
plt.show()

중요도 값과 표준편차는 약간의 차이가 있으나 무시할 수 있는 정도로 보인다. 변수 중요도 값이 차이가 나는 것은 재배열 과정에서 랜덤성이 들어갔기 때문에 당연한 것이다. 중요도는 두 경우 모두
$$x_4 > x_5 > x_3 > x_2 > x_1 > x_6 > x_8 = x_7 = x_0 $$
순으로 나타났으며 $x_4$가 예측력과 관련하여 가장 큰 영향력을 행사하였다. MDI에서의 변수 중요도를 상기시켜보면 $x_4, x_5, x_3$까지 변수 중요도 순서는 일치했으나 다른 변수에 대해서는 Permutation Importance와 MDI가 차이를 보였다.
d. 장단점
- 장점 -
a. 예측 모형 클래스에 상관없이 적용 가능하다.
MDI는 트리 기반 모형에 대해서만 사용할 수 있었다면 Permutation Importance는 예측 모형 클래스에 관계없이 적용 가능하다.
b. 재훈련 과정이 필요 없다.
특정 변수에 대한 영향력을 변수가 있을 때와 없을 때를 나누어 모델을 두 번 훈련시킨 결과를 가지고 계산하는 경우도 있는데 Permutation Importance는 이러한 훈련을 두번 할 필요가 없다.
- 단점 -
a. 일반화 관점에서 변수 중요도를 본다면 별도의 검증 데이터 셋이 필요하다.
b. 데이터 개수에 따른 계산량이 많다.
Permutation Importance는 특히 데이터 개수가 많아지면 재배열이 충분히 대표성을 갖도록 반복 횟수를 크게 해야 하며 이에 따라 계산량이 많아진다.
c. 예측력(정확도, 평균잔차제곱) 계산을 위해 출력 값이 필요하다.
라벨이 없는 데이터는 예측력을 계산할 수 없고 이에 따라 Permutation Importance를 계산할 수 없다.
d. 변수간 상관성이 있다면 변수 중요도는 편향적(Biased) 일 수도 있다.
e. 유니크 값이 많은 연속형 변수들의 중요도가 범주형 변수보다 과도하게 높은 경향성을 나타낸다.
이번 포스팅에서는 변수 중요도에 대해서 정리해보았다. 이번 기회에 어렴풋이 알던 지식을 좀 더 심화한 것 같아서 뿌듯했다.
- 참고 자료 -
4.2. Permutation feature importance - https://scikit-learn.org/stable/modules/permutation_importance.html

'통계 > 머신러닝' 카테고리의 다른 글
| 28. K-Modes Clustering(클러스터링, 군집화)에 대해서 알아보자 with Python (383) | 2022.09.04 |
|---|---|
| 27. Partial Dependence Plot (부분 의존도 그림), Individual Conditional Expectation Plot (개별 조건부 평균 그림)에 대해서 알아보자 with Python (0) | 2022.09.02 |
| 25. Shapley Value와 SHAP에 대해서 알아보자 with Python (19) | 2022.08.25 |
| 24. 랜덤 포레스트(Random Forest)에 대해서 알아보자 (3) | 2022.08.05 |
| 23. 배깅(Bagging)에 대해서 알아보자 (0) | 2022.07.20 |





댓글