딥러닝이 나타나기 전에 전성기를 구가했던 서포트 벡터 머신(Support Vector Machine)에 대해서 공부한 내용을 포스팅하려고 한다. 서포트 벡터 머신에 대한 개념과 종류 그리고 파이썬으로 구현하는 방법을 소개한다. 구현은 직접 구현을 해보고 Scikit-learn에서 제공하는 것과 비교하려고 한다.
이번 포스팅에서 다루는 내용은 다음과 같다.
1. 서포트 벡터 머신(Support Vector Machine)이란?
2. 서포트 벡터 머신(Support Vector Machine) 종류
3. 서포트 벡터 머신(Support Vector Machine) 장단점
이곳은 꽁냥이가 머신러닝을 공부한 내용을 정리하는 곳입니다.
이 포스팅에서는 수식을 포함하고 있습니다. 티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니 웹브라우저 또는 모바일 웹브라우저로 보시길 바랍니다.
1. 서포트 벡터 머신(Support Vector Machine)이란?
먼저 서포트 벡터 머신(Support Vector Machine)의 정의는 다음과 같다.
서포트 벡터 머신(Support Vector Machine)은 여백(Margin)을 최대화하는 초평면(Hyperplane)을 찾는 지도 학습 알고리즘이다.
이 말의 의미를 하나하나 살펴보자.
a. 여백(Margin)의 의미
서포트 벡터 머신(Support Vector Machine)을 이야기할 때에는 여백(Margin)이라는 단어가 항상 등장하게 된다. 여기서 말하는 여백(Margin)은 주어진 데이터가 오류를 발생시키지 않고 움직일 수 있는 최대 공간이다.
여백의 개념은 서포트 벡터 머신(Support Vector Machine)을 분류 문제(Classification)에 적용하느냐 아니면 회귀 문제(Regression)에 적용하느냐에 따라서 약간 다르다(개념은 똑같지만 분류 문제와 회귀 문제의 정의가 약간 다르다는 의미이다).
- 분류 문제에서의 여백(Margin)의 의미 -
먼저 분류 문제에서의 여백(Margin)의 의미를 알아보자. 먼저 아래 그림에서 입력 데이터가 2차원이고 라벨은 파란색과 빨간색 두 클래스가 있다고 해보자. 이때 이를 분류하는 초평면을 초록색 직선이라고 하고 직선 윗부분을 파란 클래스, 아랫부분을 빨간 클래스로 예측한다고 해보자. 여기서 개별 데이터에 대하여 직선과의 거리를 생각할 수 있다. 이때 모든 데이터에 대해서 생각할 필요는 없고 직선과 가까운 부분(1번 파란 점)에서의 거리만을 고려하자. 이때 파란색 1번 데이터가 직선과 수직인 방향으로 움직인다고 해보자. 이때 수직인 방향으로 점점 움직이다가 직선과의 거리를 초과한다면 직선 아랫부분에 놓이게 되고 이 직선은 해당 데이터를 파란색이 아닌 빨간색으로 예측하게 되어 오류가 발생한다.
따라서 파란색 1번 데이터와 직선과의 거리가 여백(Margin)이 되는 것이다(이를 넘어가면 오류를 발생시키므로).

- 회귀 문제에서의 여백(Margin)의 의미-
다음으로 회귀 문제에서의 여백(Margin)의 의미를 알아보자. 여기서는 문제를 단순화하기 위하여 단순 선형 모형(설명 변수 1개)을 생각해보겠다. 서포트 벡터 머신(Support Vector Machine)을 회귀 문제에 적용할 때에는 기본적으로 데이터들이 초평면으로 부터 $\epsilon >0$ 범위 내에 있다고 가정한다. 즉, 아래 그림과 같이 데이터들은 초록색 직선으로부터 $\epsilon$ 범위(양쪽 점선 사이)에 있는 상황이다. 이때 입력 데이터는 1차원이므로 $x$축 상에서 왔다 갔다 할 것이다. 여기서는 양 점선 사이의 수평 거리를 생각해보자. 이때 1번 데이터가 이 수평거리를 넘어가게 된다면 $\epsilon$ 범위를 넘어가게 되어 오류를 발생시킨다.
따라서 이 경우에는 양 점선 사이의 수평 거리가 여백(Margin)이 되는 것이다. 물론 한 데이터에서 양쪽 직선과의 수평 거리 중 가까운 값을 여백으로 해도 괜찮지만 나중에 수식을 유도하는 과정에서 편의성을 고려하여 양 점선 사이의 거리를 여백으로 정의한 것이다.

b. 서포트 벡터 머신(Support Vector Machine)은 여백(Margin)을 최대화하는 초평면을 찾는다.
서포트 벡터 머신(Support Vector Machine)은 여백(Margin) 최대화하는 초평면을 찾는다. 즉, 여러 초평면이 있다면 여백(Margin)을 최대화하는 것이 좋다는 의미이다. 이것이 왜 좋은지 알아보자.
- 분류 문제 -
먼저 아래 그림에서 두 클래스를 분류하는 두개의 초록색 실선이 있다고 해보자. 두 개의 직선은 모두 파란색과 빨간색을 완벽하게 분류한다. 하지만 왼쪽 여백(검은선)이 오른쪽보다 더 크다. 앞에서 여백(Margin) 주어진 데이터가 오류를 발생시키지 않고 움직일 수 있는 최대 공간이라고 했다. 그렇다면 여백이 크다는 의미는 (주어진 데이터가 아닌) 새로운 데이터가 들어왔을 때 오류를 발생시키지 않도록 확보된 공간이라는 뜻이다. 이러한 관점에서 여백이 크면 클 수록 새로운 데이터가 오류를 발생시키지 않을 가능성이 크다는 것이다. 다시 말해 여백이 크다는 것이 일반화 관점에서 좋은 것이다.
서포트 벡터 머신은 학습 데이터에 대해서 완벽하게 분리한다면 이왕이면 여백이 큰 평면을 찾는 것이다.
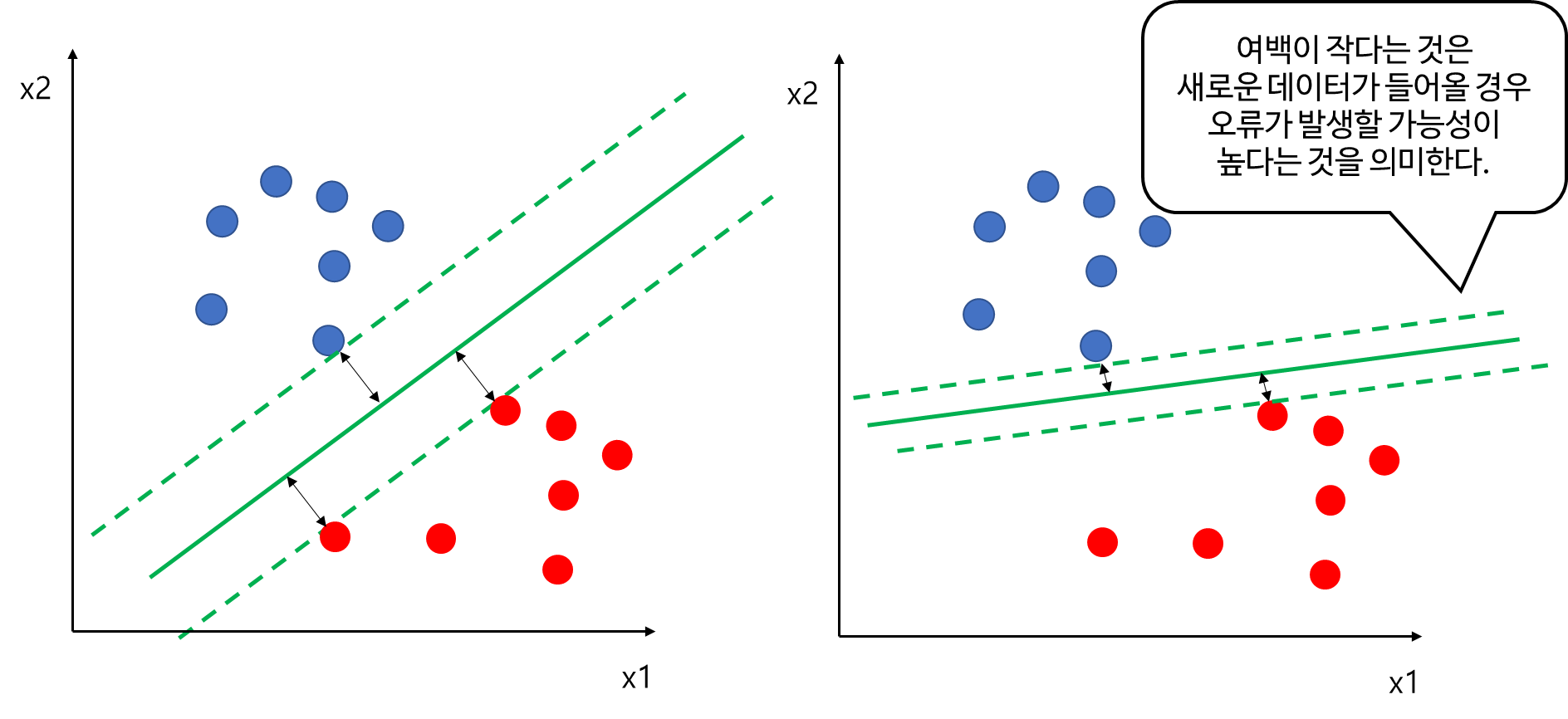
- 회귀 문제 -
회귀 문제도 분류 문제에서 설명했던 것과 같다. 아래 두 직선은 모두 $\epsilon$ 범위 내에 데이터를 포함하고 있다. 이때 여백(빨간 선)을 보면 왼쪽이 오른쪽보다 더 크다. 분류 문제에서와 마찬가지로 서포트 벡터 머신(Support Vector Machine)은 일반화 관점에서 여백이 큰 왼쪽 직선을 선호하게 된다.

c. 서포트 벡터 머신(Support Vector Machine)은 지도 학습 알고리즘이다.
서포트 벡터 머신(Support Vector Machine)은 라벨 또는 종속 변수가 있는 데이터를 학습한뒤 라벨(또는 종속변수)를 예측하게 되는 지도 학습 알고리즘이다.
d. Remind
이제 서포트 벡터 머신(Support Vector Machine)의 정의를 더 잘 이해할 수 있을 것이다. 다시 한번 외쳐보자.
서포트 벡터 머신(Support Vector Machine)은 여백(Margin)을 최대화하는 초평면(Hyperplane)을 찾는 지도 학습 알고리즘이다.
2. 서포트 벡터 머신(Support Vector Machine) 종류
여기서는 크게 분류 문제와 회귀 문제를 위한 서포트 벡터 머신으로 나누어 그 종류를 소개하고자한다. 먼저 우리에겐 데이터 $(x_i, y_i), i=1, \ldots, n$이 있다. $x_i$는 $p$차원 벡터이고 분류 문제인 경우 $y_i\in \{-1, 1\}$, 회귀 문제인 경우 $y_i\in \mathbb{R}$이다.
(1) 분류를 위한 서포트 벡터 머신(SVM for Classification)
(2) 회귀를 위한 서포트 벡터 머신(SVM for Regression)
(1) 분류를 위한 서포트 벡터 머신(SVM for Classification)
여기서는 라벨이 1, -1인 이진 분류를 가지고 설명한다. 다중 분류는 One vs One 방법을 이용하여 확장할 수 있다.
a. Hard-Margin Linear SVM
Hard의 의미는 아래와 같이 초평면을 기준으로 오분류를 허용하지 않고 완벽하게 분류하는 것을 의미한다. 실수를 허용하지 않겠다는 의미에서 'Hard'라는 의미를 썼다. 이 경우를 'Linear Separable'이라고 한다.

이제 Margin(여백)의 정의를 알아보자. 아래 그림에서 $r$이 Margin이 된다. 즉, 주어진 초평면(초록색 직선)으로부터 가장 가까운 데이터의 거리를 2배 한 것이다.

그리고 Linear라는 말은 초평면 함수가 입력 변수 $x_i$에 대하여 선형이라는 것이다.
Hard-Margin Linear SVM은 Margin을 최대화하는 초평면을 찾는 것이며 제약 조건은 모든 데이터들이 초평면으로부터의 거리가 $\frac{1}{2}r$이상 떨어져야 한다. 이를 수식으로 나타내면 다음과 같다.
$$\begin{align} \text{Find } w, b \;\;\text{ s.t Maximize }\;\; r \\ \text{Subject to }\;\; d_i \geq \frac{1}{2}r \;\; \forall i\end{align}\tag{1}$$
여기서 $d_i$는 데이터에서 초평면까지의 거리이다.
식 (1)에서 우리가 최대화해야 하는 목적함수는 $r$이다. 이를 우리가 찾고자 하는 $w, b$로 나타내 보자. 설명의 편의를 위하여 위 그림의 예시를 이용하여 유도하고자 한다. 이 예시에서 파란색은 1, 빨간색은 -1로 라벨링 되어있다. 먼저 +로 표시된 데이터의 입력 변수 좌표를 $(x_1', x_2')$라 하자.
그렇다면 $(x_1', x_2')$은 초록색 실선 위에 있으므로 $w_1x_1'+w_2x_2'+b >0$이다. 이때 임의의 양수 $a$에 대하여
$$w_1x_1'+w_2x_2'+b=a(>0)\tag{2}$$
라 하자. 그렇다면 $(x_1', x_2')$부터 초록색 직선까지의 거리는 다음과 같이 표현할 수 있다.
$$\frac{1}{2}r = \frac{|w_1x_1'+w_2x_2'+b|}{\|w\|} = \frac{a}{\|w\|}$$
여기서$\|w\| = \sqrt{w_1^2+w_2^2}$이다. 따라서 여백(Margin) $r$은 다음과 같다.
$$r = \frac{2a}{\|w\|}$$
위의 파란 데이터들은 아래와 같은 부등식을 만족할 것이다.
$$w_1x_1+w_2x_2+b\geq a$$
마찬 가지로 빨간 데이터들은 아래와 같은 부등식을 만족할 것이다.
$$w_1x_1+w_2x_2+b\leq -a$$
이를 종합하면 $|w_1x_1+w_2x_2+b|\geq a$가 되며 이것을 새로운 제약조건으로 설정한다. 즉, $x_i = (x_{i1}, x_{i2})$라 하면 새로운 제약조건은 아래와 같다.
$$|w_1x_{i1}+w_2x_{i2}+b|\geq a \;\;\forall i$$
그런데 $y_i$는 파란색은 +1, 빨간색은 -1이므로 이러한 사실을 이용하면 위 조건은 다음과 같이 쓸 수 있다.
$$y_i(w_1x_{i1}+w_2x_{i2}+b) \geq a \;\;\forall i$$
이때 $a$는 임의의 양수로 잡았으므로 편의를 위하여 1로 고정시키자. 이때 (1)은 다음과 같이 변환할 수 있다.
$$\begin{align} \text{Find } w, b \;\;\text{ s.t Maximize }\;\; \frac{2}{\|w\|} \\ \text{Subject to }\;\; y_i(w_1x_{i1}+w_2x_{i2}+b) \geq 1 \;\; \forall i\end{align}\tag{3}$$
$2/ \|w\|$를 최대화하는 것은 $\|w\|$를 최소화하는 것과 같다. 따라서 식 (3)은 최종적으로 다음과 같이 변환된다.
$$\begin{align} \text{Find } w, b \;\;\text{ s.t Minimize }\;\; \|w\| \\ \text{Subject to }\;\; y_i(w_1x_{i1}+w_2x_{i2}+b) \geq 1 \;\; \forall i\end{align}\tag{4}$$
(4)는 입력 변수의 차원이 2인 경우이므로 이를 일반화하면 다음과 같다.
$$\begin{align} \text{Find } w, b \;\;\text{ s.t Minimize }\;\; \|w\| \\ \text{Subject to }\;\; y_i(w^tx_i+b) \geq 1 \;\; \forall i\end{align}\tag{5}$$
여기서 $w = (w_1, \ldots, w_p)^t$이다.
Hard-Margin Linear SVM에서의 초평면은 위 (5)를 풀어야 한다. 이는 Quadratic Programming 방법을 이용하여 풀 수 있다. Quadratic Programming에 대한 내용은 여기서 다루진 않겠다.
(5)를 풀어서 얻은 $w, b$과 입력 값 $x$이 주어지면 다음과 같이 라벨을 예측한다.
$$\text{sign} (w^tx+b)$$
b. Soft-Margin Linear SVM
앞에서 Hard-Margin Linear SVM을 살펴보았다. 이는 클래스들이 선형 함수로 완벽하게 분리되어있는 Linear Separable 한 경우에만 쓸 수 있다. 하지만 현실세계에서 Linear Separable한 경우는 거의 없다. 즉, 선형 함수에 의해 완벽하게 분리되는 경우가 없다는 것이다. 아래 그림처럼 말이다.
이 경우에는 Margin을 최대화하되 오분류를 어느 정도 허용하는 방법을 생각할 수 있다. 오분류를 허용한다는 뜻에서 Soft라는 단어가 들어간 것이다.

먼저 아래 그림에서 주어진 초평면(초록색 직선)에 대하여 오분류된 데이터 하나를 '+'표시로 해두었다. 여기에 입력 변수는 $(x_1', x_2')$이고 라벨은 $y' = 1$인 상황이다.
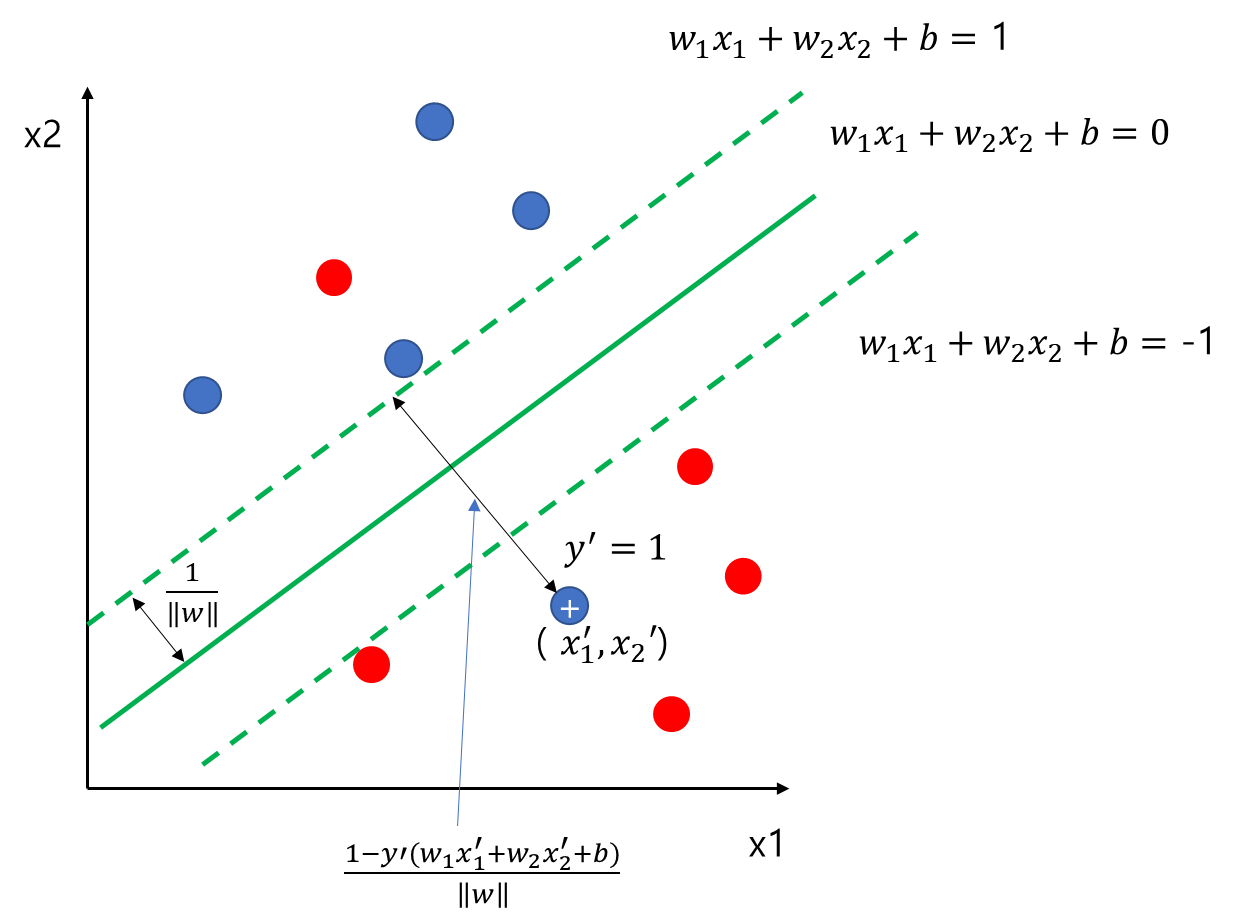
위쪽 점선과 '+'표시의 데이터 사이의 거리는
$$\begin{align} \frac{|w_1x_1'+w_2x_2'+b-1|}{\|w\|} &= \frac{1-(w_1x_1'+w_2x_2'+b)}{\|w\|} \\ &= \frac{1-y'(w_1x_1'+w_2x_2'+b)}{\|w\|} \end{align}$$
이 된다. 첫 번째 등식은 '+' 데이터가 위쪽 점선 아래에 있으므로 $w_1x_1'+w_2x_2'+b-1<0$을 만족하기 때문에 성립한다. 두 번째 등식은 $y'=1$이므로 성립한다.
여기서 $1-y'(w_1x_1'+w_2x_2'+b)$는 반쪽 여백(Margin) $1/\|w\|$을 1로 스케일을 조정한 후의 '+'와 윗쪽 점선과의 거리가 된다.
이때 $\xi = \max (0, 1-y'(w_1x_1'+w_2x_2'+b))$라 하자. $\xi(\geq 0)$는 라벨이 1인 데이터가 위쪽 점선 경계 혹은 위에 있다면 0, 아래쪽에 있다면 데이터와 윗쪽 경계선과의 (스케일 조정 후) 거리가 되며 그 값은 멀어질 수록 커진다.
이때 다음 관계를 주목해야한다.
$\xi = 0$인 경우
$$ 1-y'(w_1x_1'+w_2x_2'+b)< 0 \Rightarrow y'(w_1x_1'+w_2x_2'+b) > 1 \geq 1-\xi$$
$\xi > 0$인 경우
$$y'(w_1x_1'+w_2x_2'+b) = 1-\xi$$
만약의 빨간 데이터라면 윗쪽 점선 대신 아래쪽 점선을 이용하여 비슷한 논의를 할 수 있다. 이제 모든 데이터에 대하여 $y_i(w_1x_{i1}+w_2x_{i2}+b)$를 계산하여 $1-\xi_i$와 비교하면 아래 그림과 같다.

모든 데이터에 대하여 $y_i(w_1x_{i1}+w_2x_{i2}+b)\geq 1-\xi_i$이다.
데이터가 점선 밖에서 제대로 분류된 경우는 $\xi_i=0$이고 그렇지 않은 경우에는 $\xi_i > 0$이다. 따라서 $\xi_i>0$인 경우를 오분류가 난 경우로 해석할 수 있다. 물론 $\xi_i>0$인 경우도 점선과 실선 사이에 있다면 학습 오류는 발생하지 않으나 여백이 좁아져 테스트 오류가 발생할 수 있으므로 이러한 관점에서 오분류가 났다고 해석하는 것이다.
이 얘기를 왜 하냐 하면 초평면을 찾는 문제에서 오분류를 너무 많이 허용하면 안 되므로 오분류가 많아 짐에 따라 적절한 벌점항(Penalized Term)이 있어야 할 것이고 $\xi_i$를 이용하여 벌점항을 만들 것이기 때문이다. 따라서 (5)의 최소화하려는 목적함수에 벌점항을 추가한 새로운 목적함수를 최소화하게 된다.
$$\begin{align} \text{Find } w, b \;\;\text{ s.t Minimize }\;\; \|w\| + C\sum_{i=1}^n \xi_i \\ \text{Subject to } y_i(w^tx_i+b) \geq 1-\xi_i \;\; \forall i \\ \;\; \xi_i\geq 0 \;\;\;\;\;\;\;\;\; \forall i \end{align}\tag{6}$$
여기서 $C>0$ 이고 우리가 미리 정해주는 상수이다.
Soft-Margin Linear SVM은 (6)을 풀어서 초평면을 찾게 되고 (6)은 Quadratic Programming을 이용하여 풀 수 있다.
이 문제를 Dual Problem으로 표현해보자. (6)을 이용하여 Lagrange 함수를 정리하면 다음과 같다. 이때 $\|w\|$를 최소화하는 문제를 $w^tw/2$를 최소화하는 문제로 바꾸었다.
$$L = \frac {1}{2} w^tw+C\sum_{i=1}^n\xi_i-\sum_{i=1}^n\alpha_i \left [ (w^tx_i+b) y_i-1+\xi_i \right ]-\sum_{i=1}^n\eta_i \xi_i\tag{7}$$
여기서 $\alpha_i, \eta_i \geq 0, \forall i$이다. 우리는 KKT 조건을 살펴볼 것이다. KKT 조건은 Convex Optimization에서는 Duality Gap이 0이 되기 위한 필요충분조건이 되므로 (7)을 최소화하는 $\alpha_i, \eta_i$를 찾는 것이 (6)을 푸는 것과 동치가 된다. KKT 조건에 대한 내용은 여기를 참고하기 바란다.
이제 KKT 조건을 정리해보자.
(Stationary)
$$\begin{align}\frac{\partial L}{\partial b} &= -\sum_{i=1}^n\alpha_iy_i = 0 \Rightarrow \sum_{i=1}^n\alpha_iy_i = 0 \tag{K.1}\\ \frac{\partial L}{\partial w} &= w-\sum_{i=1}^n\alpha_iy_ix_i = 0 \Rightarrow w = \sum_{i=1}^n\alpha_iy_ix_i \tag{K.2} \\ \frac{\partial L}{\partial \xi_i} &= C-\alpha_i-\eta_i = 0, \;\; \forall i \tag{K.3} \end{align}$$
(Complementary Slackness)
$$\begin{align} \alpha_i\left [ y_i(w^tx_i+b)-1+\xi_i \right ] = 0, \;\; \forall i\tag{K.4} \\ \eta_i\xi_i = 0 \Rightarrow (C-\alpha_i)\xi_i = 0, \;\; \forall i\tag{K.5} \end{align}$$
위 조건들을 이용하여 (7)을 다시쓰면 다음과 같다.
$$\begin{align} L&= \frac{1}{2}\sum_{i}\sum_{j}\alpha_i\alpha_jy_iy_jx_i^tx_j - \sum_{i}\sum_{j}\alpha_i\alpha_jy_iy_jx_i^tx_j \\ &-b\sum_i\alpha_iy_i + \sum_i\alpha_i + \sum_i(C-\alpha_i-\eta_i)\xi_i \\ &= -\frac{1}{2}\sum_{i}\sum_{j}\alpha_i\alpha_jy_iy_jx_i^tx_j + \sum_i\alpha_i \end{align}$$
여기서 $\alpha_i, \eta_i \geq 0$과 (K.3)을 이용하면 $0\leq \alpha_i \leq C$인 것을 알 수 있다. 즉, (6)은 다음과 같이 바꿔 쓸 수 있다. $L$을 최대화해야 하는데 -1을 곱해서 최소화하는 문제로 바꿨다.
$$\begin{align} \text{Find } \alpha \;\;\text{ s.t Minimize }\;\; \frac{1}{2}\alpha^tQ\alpha-e^t\alpha \\ \text{Subject to } y^t\alpha=0 \\ \;\; 0\leq \alpha_i \leq C, \;\forall i \end{align}\tag{8}$$
여기서 $\alpha = (\alpha_1, \ldots, \alpha_n)^t, y=(y_1, \ldots, y_n)^t$, $e=(1, \ldots , 1)^t$ 그리고 $Q$는 $Q_{ij} = y_iy_jx_i^tx_j$인 $n\times n$행렬이다.
즉, (8)에 해를 찾고 KKT 조건을 이용하여 $w, b$를 찾으면 이것이 (6)의 해가 된다.
그런데 $w$는 (K.2)를 이용하여 쉽게 구할 수 있는 반면 $b$를 구하는 게 약간 어렵다.
먼저 다음의 인덱스 셋 $I$을 찾는다.
$$I = \{ i \in \{1, \ldots, n \} : 0 < \alpha_i < C \}$$
$i \in I$에 대하여 (K.5)에 의해 $\xi_i = 0$이고 (K.4)에 의하여 $ y_i(w^tx_i+b)-1 = 0$이다. 이를 이용하면 $b$는 다음과 같이 구할 수 있다(양변에 $y_i$를 곱한 뒤 $b$에 대해서 정리한다).
$$b = y_i-w^tx_i = y_i-\sum_{j=1}^n\alpha_jy_jx_j^tx_i \tag{9}$$
이때 최종적으로 $b$는 다음과 같이 계산한다.
$$b =\frac{1}{|I|} \sum_{i\in I}(y_i-w_i^tx_i) =\frac{1}{|I|} \sum_{i\in I}(y_i-\sum_{j=1}^n\alpha_jy_jx_j^tx_i)$$
여기서 $|I|$는 $I$의 원소 개수이다.
위에서 얻은 $w, b$와 입력값 $x$를 가지고 다음과 같이 예측하게 된다.
$$\text{sign} (w^tx+b)$$
만약 $I$가 공집합이라면 아래 부등식 하한과 상한의 중간 지점을 $b$로 선택한다.
$$\begin{align} & \min \{y_i\nabla_if(\alpha) | \alpha_i=0, y_i = -1 \;;\text{or}\;; \alpha_i=C, y_i=1 \} \\ \leq & b \\ \leq & \max \{y_i\nabla_if(\alpha) | \alpha_i=0, y_i = 1 \;;\text{or}\;; \alpha_i=C, y_i=-1 \} \end{align}$$
여기서 $f(\alpha) = \frac{1}{2}\alpha^tQ\alpha-e^t\alpha$이고 $\nabla_if(\alpha)$는 $f(\alpha)$의 그라디언트 벡터에서 $i$번째 원소를 말한다.
c. Soft-Margin Nonlinear SVM
지금까지는 초평면이 입력 변수에 대하여 선형이었다. 현실 세계에서는 선형 평면으로 분류되는 경우는 거의 없다. 따라서 입력 변수에 대한 복잡한 관계(비선형 관계)를 갖는 초평면이 필요하게 된다. 이는 입력 변수의 적절한 변환 $\phi$를 이용하면 입력 변수를 마치 고차원 입력 변수로 확장시킬 수 있고 기존에 선형 평면으로 분류하지 못했던 것을 분류할 수 있게 된다.
아래의 그림과 같이 (2 분류) 데이터가 있다면 선형 평면으로는 절대 완벽하게 분류할 수 없다.
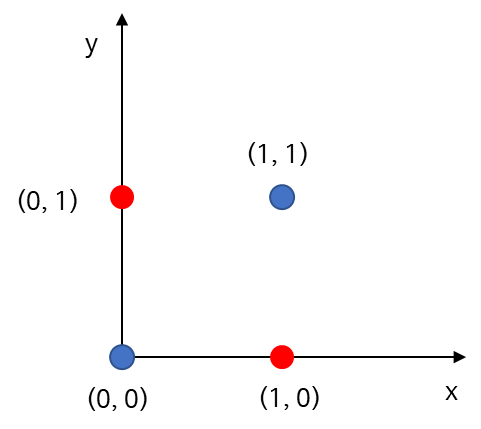
이를 어떻게 해결할 수 있을까? 먼저 2차원 입력 변수 공간(Input Space)에서 3차원으로 가는 맵 $\phi$를 다음과 같이 정의해보자.
$$\phi((x_1, x_2)) = (x_1^2, \sqrt{2}x_1x_2, x_2^2)^t$$
Nonlinear SVM은 아래 그림과 같이 위 데이터를 $\phi$로 변환한 초평면(오른쪽 초록 평면)을 찾게 된다. 이렇게 하면 기존 선형 평면으로 분류하지 못했던 것을 분류할 수 있게 된다.

변환 $\phi$가 주어진 경우 우리는 다음을 최적화하게 된다.
$$\begin{align} \text{Find } \alpha \;\;\text{ s.t Minimize }\;\; \frac{1}{2}\alpha^tQ\alpha-e^t\alpha \\ \text{Subject to } y^t\alpha=0 \\ \;\; 0\leq \alpha_i \leq C, \;\forall i \end{align}\tag{10}$$
여기서 $\alpha = (\alpha_1, \ldots, \alpha_n)^t, y=(y_1, \ldots, y_n)^t$, $e=(1, \ldots , 1)^t$ 그리고 $Q$는 $Q_{ij} = y_iy_j\phi(x_i)^t\phi(x_j)$인 $n\times n$행렬이다.
(10)을 풀어서 얻은 $w, b$를 이용하여 다음과 같이 예측한다($w, b$를 구하는 것은 Soft-Margin Linear SVM에서와 비슷한 방법으로 계산한다. 즉, $x$를 $\phi(x)$로 바꾸면 된다).
$$\text{sign} (w^t\phi(x)+b)$$
d. Nonlinear SVM with Kernels
우리는 $\phi$를 이용하여 입력 변수에 대한 선형 초평면을 비선형 초평면으로 확장시켰다. 하지만 $\phi$의 차원이 커지면 $\phi$자체의 계산량뿐 아니라 내적 $\phi(x_i)^t\phi(x_j)$ 계산량도 많아지게 된다.
이러한 계산량을 줄이고자 커널 $k$를 도입하게 되었다. $k$는 암묵적으로 다음과 같은 관계에 있다고 가정한다.
$$k(x_i, x_j) = \phi(x_i)^t\phi(x_j)$$
즉, $k$가 주어지면 눈에는 보이지 않지만 어떤 $\phi$가 있어서 위와 같은 관계를 갖는 것이다. 왜 눈에 보이지 않느냐고 했냐면 $\phi$가 주어진 경우 $k$는 명확하게 나타낼 수 있지만 $k$가 주어진 경우에 위 관계를 만족하는 $\phi$를 찾기가 쉽지 않기 때문이다.
커널 $k$를 정했다면 (10)에서 행렬 $Q$를 $Q_{ij} = y_iy_jk(x_i, x_j)$로 하여 최적화 문제를 풀게 된다.
자주 사용하는 커널은 다음과 같다.
(Polynomial Kernel)
$$k(x, y) = (\gamma x^ty+\theta)^d, \gamma>0$$
(RBF Kernel)
$$k(x, y) = \exp (-\gamma \| x-y \|^2), \gamma>0 $$
(Sigmoid Kernel)
$$k(x, y) = \tanh(\gamma x^ty+\theta), \gamma>0 $$
그렇다면 예측은 어떻게 할까?
먼저 Soft-Margin Nonlinear SVM에서 $w, b$는 다음과 같이 계산된다.
$$\begin{align} w &= \sum_{i=1}^n\alpha_iy_i\phi(x_i) \\ b &= \frac{1}{|I|}\sum_{i\in I}(y_i-\sum_{j=1}^n\alpha_jy_j \phi(x_j)^t\phi(x_i)) \end{align} \tag{11}$$
그리고 입력 변수 $x$에 대하여 예측은 다음과 같이 하게 된다.
$$\text{sign} (w^t\phi(x)+b) = \text{sign} (\sum_{i=1}^n\alpha_iy_i\phi(x_i)^t\phi(x)+b)\tag{12}$$
커널 $k$를 이용하면 (11)에서 $b$는
$$b = \frac{1}{|I|}\sum_{i\in I}(y_i-\sum_{j=1}^n\alpha_jy_j k(x_i, x_j))$$
이 되고 예측은 (12)에서
$$\text{sign} (\sum_{i=1}^n\alpha_iy_ik(x_i, x)+b)$$
e. 고려 사항
상수 $C$는 교차 검증을 통하여 선정한다. 커널의 선택은 사전 지식이 없다면 기본적으로 RBF 커널을 쓰는 것이 좋다고 한다. 그리고 커널에 포함된 모수(예: Polynomial Kernel의 경우 $d$)는 교차 검증을 통하여 선정한다.
(2) 회귀를 위한 서포트 벡터 머신(SVM for Regression)
이번엔 서포트 벡터 머신을 회귀에 적용하는 방법에 대해서 알아본다.
a. Hard-Margin Linear SVM
Hard-Margin Linear SVM은 모든 데이터가 오차 $\epsilon$에 있으면서 여백을 최대화하는 선형 함수를 구하게 된다.
예를 들어보자. 여기서는 입력 변수가 한 개인 경우이다. 주어진 직선(초록색 실선)에 대하여 모든 데이터는 오차 $\epsilon$ 범위 내에 있고 여백은 빨간 선과 같다.
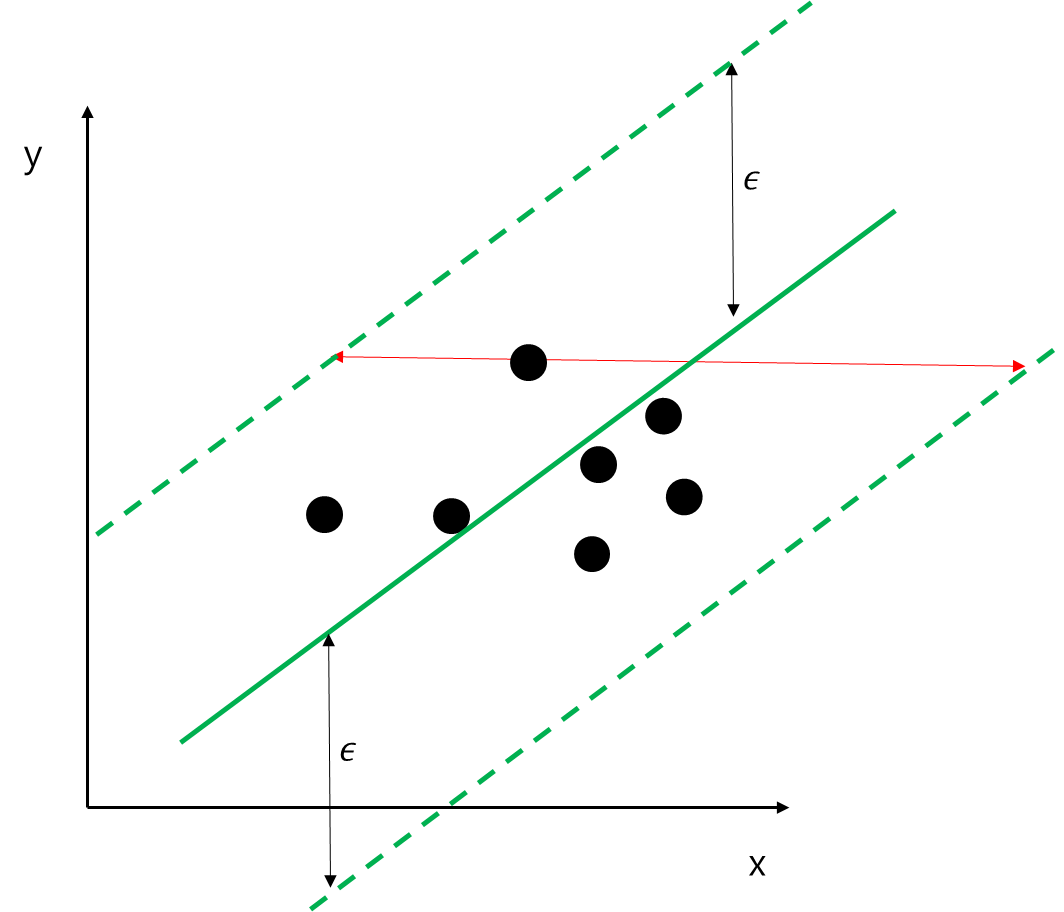
여백을 $w, b$로 표현해보자. 먼저 빨간색 화살표와 양쪽 점선이 만나는 좌표를 각각 $(x_1, y), (x_2, y)$라 하자($y$좌표는 같다는 것에 주목하자). 그렇다면 여백은 $|x_1-x_2|$가 된다.

이를 다르게 표현하면
$$\begin{align} |x_1-y_1| &= |y-b+\epsilon - (y-b-\epsilon)|/|w| \\ &= 2\epsilon/|w| \end{align}$$
이다.
이때 여백(Margin)을 최대화하는 것은 $\frac{1}{2}|w|^2$을 최소화하는 것과 같다. 또한 모든 데이터는 $y_i-wx_i-b\leq \epsilon$ 또는 $wx_i+b-y_i\leq \epsilon$이어야 한다.
이를 일반화하면 Hard-Margin Linear SVM은 다음과 같은 최적화 문제를 풀게 된다.
$$\begin{align} \text{Find } w, b \;\;\text{ s.t Minimize }\;\; \frac{1}{2}\|w\|^2 \\ \text{Subject to }\;\;\begin{cases} y_i-w^tx_i-b \leq \epsilon \\ w^tx_i+b-y_i \leq \epsilon \end{cases} \end{align}\tag{13}$$
위 문제는 Quadratic Programming을 이용하여 풀 수 있다. (13)의 해를 $w, b$라 하면 예측값은 다음과 같이 계산한다.
$$w^tx+b$$
b. Soft-Margin Linear SVM
앞에서 살펴본 Hard-Margin Linear SVM에서 모든 데이터가 초평면으로부터 $\epsilon$ 내에 있어야 한다는 것은 꽤나 비현실적이다. 현실에서는 $\epsilon$을 초과하는 데이터가 있기 마련이다. 아래 그림처럼 말이다.

이런 경우에는 오차범위 $\epsilon$을 초과하는 데이터를 어느 정도 허용하는 Soft 한 방법을 생각할 수 있다. 이를 위해 모든 데이터 포인트들에 대해서 다음을 계산한다.
$$\xi_i = \begin{cases} 0 & \text{ if }\; y_i-wx_i-b \leq \epsilon \\ y_i-wx_i-b-\epsilon & \text{ otherwise.} \end{cases}$$
$$\xi_i^* = \begin{cases} 0 & \text{ if }\; wx_i+b-y_i \leq \epsilon \\ wx_i+b-y_i - \epsilon & \text{ otherwise.} \end{cases}$$
그림에서 모든 데이터에 대하여 위를 계산하면 다음과 같다. 이때 $\xi_i^{(*)}$는 $\xi_i, \xi_i^*$를 통틀어 지칭한 것이다(앞으로 위 첨자에 (*)가 있다면 문맥에 따라서 이해하면 된다).

$\xi_i, \xi_i^*$를 이용하면 모든 데이터들은 다음과 같은 제약 조건을 갖고 있다는 것을 알 수 있다.
$$y_i-wx_i-b\leq \epsilon+\xi_i, \;\; wx_i+b-y_i \leq \epsilon+\xi_i^* $$
오차 범위를 넘어가는 데이터를 허용한다고 하지만 이를 너무 많이 그리고 너무 큰 오차는 허용할 순 없을 것이다. 따라서 목적함수에 벌점항을 고려해야 한다. 이를 종합하고 $x$가 1차원이 아닌 $p$차원으로 확장하여 (13)을 다음과 같이 변환한다.
$$\begin{align} \text{Find } w, b \;\;\text{ s.t Minimize }\;\; \frac{1}{2}\|w\|^2 + C\sum_{i=1}^n(\xi_i+\xi_i^*) \\ \text{Subject to }\;\;\begin{cases} y_i-w^tx_i-b \leq \epsilon + \xi_i \\ w^tx_i+b-y_i \leq \epsilon+\xi_i^* \end{cases} \end{align}\tag{14}$$
여기서 $C>0$으로 우리가 설정하는 상수이다.
(14)는 Quadratic Programming을 이용하여 풀 수 있으나 Dual 문제로 바꿔서 풀 수 있다. 이를 위해 (14)를 이용하여 Lagrange 함수를 계산해야 한다.
$$L = \frac{1}{2}\|w\|^2+C\sum_{i=1}^n(\xi_i+\xi_i^*)-\sum_{i=1}^n(\eta_i\xi_i+\eta_i^*\xi_i^*)\\-\sum_{i=1}^n\alpha_i(\epsilon+\xi_i-y_i+w^tx_i+b)\\-\sum_{i=1}^n\alpha_i^*(\epsilon+\xi_i+y_i-w^tx_i-b) \tag{15}$$
여기서 $\alpha^{(*)}\geq 0, \eta^{(*)} \geq 0$이다. 이제 KKT 조건을 구하면 다음과 같다.
(Stationary)
$$\begin{align}\frac{\partial L}{\partial b} &= \sum_{i=1}^n(\alpha_i^*-\alpha_i)= 0 \tag{K.6}\\ \frac{\partial L}{\partial w} &= w-\sum_{i=1}^n(\alpha_i^*-\alpha_i) x_i = 0 \Rightarrow w = \sum_{i=1}^n(\alpha_i^*-\alpha_i) x_i \tag{K.7} \\ \frac{\partial L}{\partial \xi_i^{(*)}} &= C-\alpha_i^{(*)}-\eta_i^{(*)} = 0, \;\; \forall i \tag{K.8} \end{align}$$
(Complementary Slackness)
$$\begin{align} \alpha_i(\epsilon+\xi_i-y_i+w^tx_i+b) &= 0 \\ \alpha_i^*(\epsilon+\xi_i+y_i-w^tx_i-b) &= 0 \tag{K.9} \\ (C-\alpha_i^{(*)})\xi_i^{(*)} = 0, \;\; \forall i \tag{K.10} \end{align}$$
(K.6)~(K.8)을 (15)에 적용하면 다음과 같다.
$$\begin{align} \text{Maximize}\;\; &\begin{cases} -\frac{1}{2}\sum_{i, j=1}^n(\alpha_i-\alpha_i^*)(\alpha_j-\alpha_j^*)x_i^tx_j \\ -\epsilon\sum_{i=1}^n(\alpha_i+\alpha_i^*)+\sum_{i=1}^ny_i(\alpha_i-\alpha_i^*) \end{cases} \\ \text{subject to}\;\; & \sum_{i=1}^n(\alpha_i-\alpha_i^*)=0 \;\text{ and }\; \alpha_i^{(*)} \in [0, C] \end{align}\tag{16}$$
$w$는 (K.7)을 이용하여 구할 수 있다. $b$를 구하기 위해 (K.9), (K.10)을 이용하면 다음을 알 수 있다.
$$\begin{align} & \epsilon-y_i+w^tx_i+b \geq 0 \;\text{ if }\; \alpha_i<C \\ & \epsilon-y_i+w^tx_i+b \leq 0 \;\text{ if }\; \alpha_i>0 \end{align}$$
$\alpha_i^*$에 대해서도 비슷한 결과를 얻을 수 있고 이를 이용하여 다음을 알 수 있다.
$$\max \{-\epsilon+y_i-w^tx_i | \alpha_i<C \text{ or } \alpha_i^*>0 \} \\ \leq b \leq \\ \min\{ -\epsilon+y_i-w^tx_i | \alpha > 0 \text{ or } \alpha_i^*<C \} $$
따라서 위 부등식의 상한과 하한의 중간값을 $b$로 한다.
참고로 $\alpha_i-\alpha_i^*$가 0이 아닌 경우 $x_i$를 서포트 벡터(Support Vector)라고 하며 모든 예측은 결국 서포트 벡터만 가지고 이루어진다. 즉, 모든 데이터가 필요하지 않다.
(K.7)을 이용하면 $x$가 주어졌을 때 예측값을 다음과 같이 계산할 수 있다.
$$f(x) = \sum_{i=1}^n(\alpha-\alpha^*)x_i^tx+b$$
c. Soft-Margin Nonlinear SVM
입력 변수와 출력 변수간 복잡한 관계를 표현하기 위하여 선형 모형은 한계가 있다. 이때 변환 $\phi$를 이용하면 입력 변수와 출력 변수간 복잡한 관계를 표현하는 함수를 만들어 낼 수 있다.
Soft-Margin Nonlinear SVM은 $x$가 아닌 $\phi (x)$를 새로운 입력 변수로 하여 Soft-Margin Linear SVM을 적용한다. 즉, 다음의 최적화 문제를 풀게 된다.
$$\begin{align} \text{Maximize}\;\; &\begin{cases} -\frac{1}{2}\sum_{i, j=1}^n(\alpha_i-\alpha_i^*)(\alpha_j-\alpha_j^*)\phi(x_i)^t\phi(x_j) \\ -\epsilon\sum_{i=1}^n(\alpha_i+\alpha_i^*)+\sum_{i=1}^ny_i(\alpha_i-\alpha_i^*) \end{cases} \\ \text{subject to}\;\; & \sum_{i=1}^n(\alpha_i-\alpha_i^*)=0 \;\text{ and }\; \alpha_i^{(*)} \in [0, C] \end{align}\tag{17}$$
Soft-Margin Linear SVM에서 했던 방식과 비슷하게 $w, b$를 얻을 수 있고 새로운 데이터 $x$가 들어왔을 때 다음과 같이 예측값을 계산한다.
$$f(x) = \sum_{i=1}^n(\alpha-\alpha^*)\phi(x_i)^t\phi(x)+b$$
d. Nonlinear SVM with Kernels
분류 문제에서 언급했듯이 여기에서도 커널을 써서 고차원 맵 $\phi$을 사용한 것과 같은 효과를 낼 수 있다. 커널을 쓰면 불필요한 내적 계산이 없어진다. 커널 $k$에 대하여 다음의 최적화 문제를 풀게 된다.
$$\begin{align} \text{Maximize}\;\; &\begin{cases} -\frac{1}{2}\sum_{i, j=1}^n(\alpha_i-\alpha_i^*)(\alpha_j-\alpha_j^*)k(x_i, x_j) \\ -\epsilon\sum_{i=1}^n(\alpha_i+\alpha_i^*)+\sum_{i=1}^ny_i(\alpha_i-\alpha_i^*) \end{cases} \\ \text{subject to}\;\; & \sum_{i=1}^n(\alpha_i-\alpha_i^*)=0 \;\text{ and }\; \alpha_i^{(*)} \in [0, C] \end{align}\tag{17}$$
이때 $b$는 아래의 상한과 하한의 중간 지점을 선택하면 된다.
$$\max \{-\epsilon+y_i-\sum_{j=1}^n(\alpha_j-\alpha_j^*)k(x_j, x_i) | \alpha_i<C \text{ or } \alpha_i^*>0 \} \\ \leq b \leq \\ \min\{ -\epsilon+y_i-\sum_{j=1}^n(\alpha_j-\alpha_j^*)k(x_j, x_i) | \alpha > 0 \text{ or } \alpha_i^*<C \} \tag{18}$$
새로운 데이터 $x$에 대하여 예측값을 다음과 같이 계산한다.
$$f(x) = \sum_{i=1}^n(\alpha-\alpha^*)k(x_i, x)+b$$
커널을 이용하면 $w$를 구하지 않아도 예측할 수 있다.
e. 고려 사항
$\epsilon$은 보통 0.1 근방의 값을 사용하며 상수 $C$는 교차 검증을 통하여 선정한다. 커널의 선택은 사전 지식이 없다면 기본적으로 RBF 커널을 쓰는 것이 좋다고 한다. 그리고 커널에 포함된 모수(예: Polynomial Kernel의 경우 $d$)는 교차 검증을 통하여 선정한다.
3. 서포트 벡터 머신(Support Vector Machine) 장단점
- 장점 -
a. 회귀와 분류 문제에 모두 적용할 수 있다.
로지스틱 회귀는 분류만 적용이 가능하나 서포트 벡터 머신은 분류뿐 아니라 회귀에도 적용 가능하다.
b. 예측력이 좋다.
로지스틱 회귀나 판별 분석은 데이터가 주어졌을 때 출력 라벨의 대한 조건부 확률을 예측한다. 따라서 실제 라벨링을 할 때에는 조건부확률을 예측하고 임계값을 정해야 한다(2번의 추정이 필요한 것이다). 하지만 서포트 벡터 머신은 확률이 아닌 라벨을 직접 추정하기 때문에 로지스틱 회귀나 판별 분석보다는 예측력이 높다.
c. 입력 변수와 출력 변수 간의 복잡한 관계를 모델링할 수 있다.
변환 $\phi$나 커널 $k$를 이용하면 입력 변수와 출력 변수간 복잡한 관계를 모형화할 수 있다.
d. 계산량의 이점과 입력 변수 차원의 덜 영향을 받는다.
데이터가 많아도 결국엔 서포트 벡터만 이용해도 모수를 완벽하게 추정할 수 있어서 계산량의 이점이 있다. 또한 커널을 이용하면 $\phi$의 차원이 높더라도 예측값을 쉽게 계산할 수 있다.
- 단점 -
a. 확률을 추정하지 못한다.
서포트 벡터 머신은 분류 문제에서 일반적으로 확률을 추정하지 못한다. 따라서 확률 추정값을 요구하는 분야에서는 큰 힘을 발휘하지 못한다. 이러한 단점을 극복하고자 분류 문제에서 Wu가 2004년 "Probability estimates for multi-class classification by pairwise coupling"이라는 논문에서 확률을 추정하는 방법을 제안하기도 했다.
b. 해석이 어렵다.
커널이나 변환 $\phi$를 사용하는 경우 입력 변수와 출력 변수간 해석이 어려워진다.
4. 파이썬 구현
이제 파이썬으로 구현해볼 시간이다. 구현은 직접 구현을 먼저 해보고 Scikit-Learn에서 제공하는 것과 비교해보려고 한다.
- 직접 구현 -
1) 코드 설명
사실 직접 구현이라고 했지만 완전 밑바닥에서부터 구현한 것은 아니다. 서포트 벡터 머신 알고리즘으로 초평면을 얻기 위해서 Quadratic Programming 알고리즘이 필요한데 이 부분은 Convex 최적화 알고리즘을 제공하는 모듈인 cvxopt을 사용했다. pip을 이용하여 설치할 수 있다.
pip install cvxopt
cvxopt에서 Quadratic Programming 알고리즘은 아래와 같은 표준화된 형식의 문제를 풀게 된다.
$$\begin{align} \;\;\text{Minimize }\;\; \frac{1}{2}x^tPx+q^tx \\ \text{Subject to } Gx \leq h \\ \;\; Ax = b \end{align}\tag{19}$$
따라서 서포트 벡터 머신 알고리즘을 위 형식에 맞게 설정만 해주면 되는 것이다.
서포트 벡터 머신을 구현한 주피터 노트북 파일은 아래에 첨부해두었다. 이에 대해서 하나씩 설명하려고 한다.
먼저 필요한 모듈을 불러오자.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from itertools import combinations
from collections import Counter
from cvxopt import matrix as cvxopt_matrix
from cvxopt import solvers as cvxopt_solvers
다음으로 이진 분류를 위한 BinarySVC 클래스를 만들어 준다. 커널 타입과 Polynomial, Sigmoid Kernel에서 $\theta$를 초기값으로 지정할 수 있다. 커널을 지정하지 않으면 자동으로 Soft-Margin Linear SVM 알고리즘이 작동된다.
class BinarySVC():
def __init__(self, kernel=None, coef0=0):
self.labels_map = None
self.kernel = kernel
self.X = None
self.y = None
self.alphas = None
self.w = None
self.b = None
self.coef0 = coef0
if kernel is not None:
assert kernel in ['poly', 'rbf', 'sigmoid']
다음으로 전처리를 위한 여러 가지 함수를 정의한다. 원 데이터의 라벨을 1, -1로 매핑하기 위한 맵을 생성하는 make_label_map 함수, 원 데이터의 라벨을 실제로 1, -1로 변환하는 transform_label 함수, 1과 -1을 원 데이터의 라벨로 바꿔주는 inverse_label 함수 그리고 마지막으로 두 벡터의 커널 값을 계산하는 get_kernel_val 함수를 만들어주었다.
class BinarySVC():
'''중략'''
def make_label_map(self, uniq_labels):
labels_map = list(zip([-1, 1], uniq_labels))
self.labels_map = labels_map
return
def transform_label(self, label, labels_map):
res = [l[0] for l in labels_map if l[1] == label][0]
return res
def inverse_label(self, svm_label, labels_map):
try:
res = [l[1] for l in labels_map if l[0] == svm_label][0]
except:
print(svm_label)
print(labels_map)
raise
return res
def get_kernel_val(self, x, y):
X = self.X
coef0 = self.coef0
gamma = 1/(X.shape[1]*X.var())
if self.kernel == 'poly':
return (gamma*np.dot(x,y)+coef0)**2
elif self.kernel == 'rbf':
return np.exp(-gamma*np.square(np.linalg.norm(x-y)))
else:
return np.tanh(gamma*np.dot(x,y)+coef0)
이제 주인공이라 할 수 있는 서포트 벡터 모형 적합 함수이다. 적합한다는 것을 알고리즘을 통하여 초평면의 모수를 얻는다는 것을 말한다.
(10)을 이용하여 cvxopt가 계산하는 Quadratic Programming 표준 형식을 맞춰준다.
$$\begin{align} x &=\alpha\;\; (n \times 1 \; \text{vector}), \\ P&=Q \;\;(n\times n \; \text{matrix}), \\ q &= -e \;\; (n \times 1 \; \text{vector}), \\ G &=\begin{pmatrix} -I \\ I \end{pmatrix} \;\; (2n \times n \; \text{matrix}), \\ h &= (0, \ldots, 0, C, \ldots, C)^t \;\; (2n \times 1 \;\text{vector}), \\ A &= y^t \;\;(1\times n \;\text{matrix}), \\ b &= 0 \;\;(\text{scalar}) \end{align}$$
여기서 $I$는 $n\times n$ 단위행렬($n$은 데이터 개수이다), $e$는 1로 이루어진 $n$차원 벡터이다. 이때 $Q$는 커널을 사용할 때와 안 할 때로 나누어 만들어주었다.
$w$은 커널을 사용하지 않는 경우에만 계산한다. $b$는 우리가 찾은 해에서 $\alpha$가 특정 값 이상인 인덱스를 구하고 이에 해당하는 $y_i$와 $x_i$를 이용하여 계산한다.
class BinarySVC():
'''중략'''
def fit(self, X, y, C):
assert C >= 0, 'constant C must be non-negative'
uniq_labels = np.unique(y)
assert len(uniq_labels) == 2, 'the number of labels is 2'
self.make_label_map(uniq_labels)
self.X = X
y = [self.transform_label(label, self.labels_map) for label in y] ## 1, -1로 변환
y = np.array(y)
## formulating standard form
m, n = X.shape
y = y.reshape(-1,1)*1.
self.y = y
if self.kernel is not None:
Q = np.zeros((m,m))
for i in range(m):
for j in range(m):
Q[i][j] = y[i]*y[j]*self.get_kernel_val(X[i], X[j])
else:
yX = y*X
Q = np.dot(yX,yX.T)
P = cvxopt_matrix(Q)
q = cvxopt_matrix(-np.ones((m, 1)))
G = cvxopt_matrix(np.vstack((np.eye(m)*-1,np.eye(m))))
h = cvxopt_matrix(np.hstack((np.zeros(m), np.ones(m) * C)))
A = cvxopt_matrix(y.reshape(1, -1))
b = cvxopt_matrix(np.zeros(1))
## cvxopt configuration
cvxopt_solvers.options['show_progress'] = False ## 결과 출력 표시 X
sol = cvxopt_solvers.qp(P, q, G, h, A, b)
alphas = np.array(sol['x'])
S = (alphas>1e-4).flatten()
if self.kernel is not None:
sum_val = 0
S_index = np.where(S==True)[0]
for s in S_index:
temp_vec = np.array([self.get_kernel_val(z, X[s]) for z in X])
temp_vec = np.expand_dims(temp_vec, axis=1)
sum_val += np.sum(y[s] - np.sum(y*alphas*temp_vec))
b = sum_val/len(S)
self.b = b
else:
w = ((y*alphas).T@X).reshape(-1,1)
b = np.mean(y[S] - np.dot(X[S],w))
self.w = w
self.b = b
self.alphas = alphas
return
다음으로 예측을 위한 함수를 만들어 주었다.
class BinarySVC():
'''중략'''
def predict(self, X):
predictions = [self._predict(x) for x in X]
return predictions
def _predict(self, x):
if self.kernel:
temp_vec = np.array([self.get_kernel_val(x, y) for y in self.X])
temp_vec = np.expand_dims(temp_vec, axis=1)
S = (self.alphas>1e-4).flatten()
res = np.sign(np.sum(self.y[S]*self.alphas[S]*temp_vec[S])+self.b)
else:
res = np.sign(self.w.T.dot(x)+self.b)
res = self.inverse_label(res, self.labels_map)
return res
이제 큰 형님이 나올 차례이다. mySVM 클래스는 분류와 회귀를 위한 서포트 벡터 머신을 구현한 클래스이다. 하나씩 살펴보자. 이 클래스는 초기값으로 서포트 벡터 머신을 회귀에 적용할지 분류에 적용하리 결정하는 변수 svm_type를 지정하고 커널과 커널에 대한 $\theta$ 값을 설정한다.
class mySVM():
def __init__(self, svm_type='classification', kernel=None, coef0=0):
assert svm_type in ['classification', 'regression']
self.svm_type = svm_type
self.kernel=kernel
self.X = None
self.y = None
self.coef0 = coef0
self.model_list = None
if kernel is not None:
assert kernel in ['poly', 'rbf', 'sigmoid']
여기서도 두 벡터에 대한 커널 값을 계산하는 함수가 필요하다. 회귀를 위한 서포트 벡터 머신에서 사용하려고 한다.
class mySVM():
'''중략'''
def get_kernel_val(self, x, y):
X = self.X
coef0 = self.coef0
gamma = 1/(X.shape[1]*X.var())
if self.kernel == 'poly':
return (gamma*np.dot(x,y)+coef0)**2
elif self.kernel == 'rbf':
return np.exp(-gamma*np.square(np.linalg.norm(x-y)))
else:
return np.tanh(gamma*np.dot(x,y)+coef0)
mySVM 클래스에서 적합은 svm_type에 따라서 이루어진다.
class mySVM():
'''중략'''
def fit(self, X, y, C, epsilon=0.1):
if self.svm_type == 'classification':
self._fit_svc(X, y, C)
else:
self._fit_svr(X, y, C, epsilon)
_fit_svc 함수는 분류를 위한 SVM 알고리즘을 수행한다. 다중 클래스인 경우 2 분류 문제로 바꾸어 One vs One 방식을 이용한다. 각 라벨의 조합에 대하여 데이터를 필터링하고 BinarySVC 클래스를 이용하여 SVM 모형을 적합한 뒤 이를 model_list에 저장한다.
class mySVM():
'''중략'''
def _fit_svc(self, X, y, C):
uniq_labels = np.unique(y)
label_combinations = list(combinations(uniq_labels, 2))
model_list = []
for lc in label_combinations:
target_idx = np.array([x in lc for x in y])
y_restricted = y[target_idx]
X_restricted = X[target_idx]
clf = BinarySVC(kernel=self.kernel, coef0=self.coef0)
clf.fit(X_restricted, y_restricted, C)
model_list.append(clf)
self.model_list = model_list
return
다음은 회귀를 위한 SVM을 적합하는 함수이다. 이때에도 (16)을 이용하여 cvxopt가 계산하는 Quadratic Programming 표준 형식을 맞춰준다.
$$\begin{align} x &=(\alpha^t, \alpha^{*t})^t \;\; (2n \times 1 \; \text{vector}), \\ P&=(I -I)^tQ(I -I) \;\;(2n\times 2n \; \text{matrix}), \\ q &= \epsilon e_{2n} - (y^t, -y^t)^t \;\; (2n \times 1 \; \text{vector}), \\ G &=\begin{pmatrix} -I & O \\ I & O \\ O & -I \\ O & I \end{pmatrix} \;\; (4n \times 2n \; \text{matrix}), \\ h &= (0, \ldots, 0, C, \ldots, C, 0, \ldots, 0, C, \ldots, C)^t \;\; (4n \times 1 \;\text{vector}), \\ A &= e_n^t(I -I) \;\;(1\times 2n \;\text{matrix}), \\ b &= 0 \;\;(\text{scalar}) \end{align}$$
여기서 $I$는 $n\times n$ 단위행렬, $O$ = $n\times n$ 영행렬($n$은 데이터 개수이다), $e_k$는 1로 이루어진 $k$차원 벡터이다. 또한 $Q$는 $Q_{ij} = x_i^tx_j$인 $n\times n$ 행렬이다(이는 변환 $\phi$나 커널 적용 여부에 따라 적절하게 변환하면 된다). 나머지는 BinarySVC에서 본 것과 동일하므로 추가 설명은 생략한다.
class mySVM():
'''중략'''
def _fit_svr(self, X, y, C, epsilon):
assert C >= 0, 'constant C must be non-negative'
assert epsilon > 0, 'epsilon C must be positive'
self.X = X
m, n = X.shape
y = y.reshape(-1,1)*1.
self.y = y
if self.kernel is not None:
Q = np.zeros((m,m))
for i in range(m):
for j in range(m):
Q[i][j] = self.get_kernel_val(X[i], X[j])
else:
Q = X.dot(X.T)
I = np.eye(m)
O = np.zeros((m, m))
sub_Q = np.hstack([I, -I])
main_Q = sub_Q.T.dot(Q.dot(sub_Q))
P = cvxopt_matrix(main_Q)
q = cvxopt_matrix(epsilon*np.ones((2*m, 1)) - np.vstack([y, -y]))
G = np.vstack([np.hstack([-I, O]), np.hstack([I, O]), np.hstack([O, -I]), np.hstack([O, I])])
G = cvxopt_matrix(G)
h = cvxopt_matrix(np.hstack([np.zeros(m), C*np.ones(m)]*2))
A = cvxopt_matrix(np.ones((m,1)).T.dot(sub_Q))
b = cvxopt_matrix(np.zeros(1))
cvxopt_solvers.options['show_progress'] = False
sol = cvxopt_solvers.qp(P, q, G, h, A, b)
sol_root = np.array(sol['x'])
alphas = sol_root[:m]
alphas_star = sol_root[m:]
S = (alphas>1e-4).flatten()
if self.kernel is not None:
sum_val = []
S_index = np.where(S==True)[0]
for s in S_index:
temp_vec = np.array([self.get_kernel_val(z, X[s]) for z in X])
temp_vec = np.expand_dims(temp_vec, axis=1)
sum_val.append(-epsilon + np.sum(y[s] - np.sum((alphas-alphas_star)*temp_vec)))
b = min(sum_val)
self.b = b
else:
w = alphas.T.dot(X)-alphas_star.T.dot(X)
w = w.reshape(-1,1)
b = -epsilon+np.min(y[S] - np.dot(X[S],w))
self.w = w
self.b = b
self.alphas = sol_root
return
마지막으로 예측해주는 함수를 만들어 주었다.
class mySVM():
'''중략'''
def predict(self, X):
if self.svm_type =='classification':
model_list = self.model_list
prediction = [model.predict(X) for model in model_list]
prediction = [Counter(pred).most_common(1)[0][0] for pred in list(zip(*prediction))]
else:
prediction = [self._predict_reg(x) for x in X]
return prediction
def _predict_reg(self, x):
if self.kernel is not None:
m, _ = self.X.shape
sol_root = self.alphas
alphas = sol_root[:m]
alphas_star = sol_root[m:]
temp_vec = np.array([self.get_kernel_val(z, x) for z in X])
temp_vec = np.expand_dims(temp_vec, axis=1)
pred = np.sum((alphas-alphas_star)*temp_vec)+self.b
else:
w = self.w
b = self.b
pred = w.dot(x)+b
pred = pred[0]
return pred2) 예제
a. 분류 문제
먼저 분류를 위한 붓꽃 데이터를 이용해서 내가 구현한 클래스가 잘 동작하는지 확인해보자.
from sklearn.datasets import load_iris
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['species'] = [iris.target_names[x] for x in iris.target]
species_to_labels = dict(zip(df['species'].unique(), range(len(df['species'].unique()))))
df['species'] = df['species'].map(species_to_labels)
df = df.rename(columns={'species':'label'})
X = df.drop('label', axis=1).values
y = df['label'].values
mySVM 클래스를 생성하고 fit을 이용하여 모형을 적합한다.
clf = mySVM(svm_type='classification')
clf.fit(X, y, C=10)
이제 학습 정확도를 계산해보자.
pred = clf.predict(X)
np.mean(y == pred)

98%가 나왔다.
이번엔 커널을 사용하여 분류 결과를 예측해보자.
for kernel in ['poly', 'rbf', 'sigmoid']:
clf = mySVM(svm_type='classification', kernel=kernel)
clf.fit(X, y, C=10)
pred = clf.predict(X)
print('커널 :', kernel, '정확도 :', np.mean(y == pred))
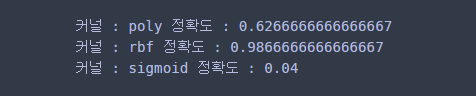
학습 정확도는 rbf를 사용했을 때 가장 높았다.
b. 회귀 문제
이번엔 보스턴 데이터를 이용하여 회귀 SVM 모형을 만들어보자.
from sklearn.datasets import load_boston
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['y'] = boston.target
X = df[['LSTAT']].values
y = df['y'].values
회귀를 적용할 땐 svm_type를 'regression'으로 바꾸어 준다. SVM 모형을 적합하고 평균 잔차 제곱을 계산해보자.
reg = mySVM(svm_type='regression')
reg.fit(X, y, C=10)
np.mean(np.square(y-reg.predict(X)))

갑자기 최종적으로 계산된 직선이 어떤 모양인지 시각화해보고 싶었다.
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(X.flatten(), y)
plt.scatter(X.flatten(), reg.predict(X))
plt.show()

파란 점이 데이터이고 주황색 선이 서포트 벡터 머신으로 추정한 곡선이다. 어느 정도 잘 적합된 거 같다 ㅎㅎ;;
이번엔 여러 가지 커널을 사용하여 서포트 벡터 머신을 적용해보았다. 여기서는 sigmoid는 제외하였다. 랭크 문제가 발생하여 에러가 나서 그렇다 ㅠㅠ
for kernel in ['poly', 'rbf']:
reg = mySVM(svm_type='regression', kernel=kernel)
reg.fit(X, y, C=10)
pred = reg.predict(X)
mse = np.mean(np.square(y-pred))
print('커널 :', kernel, 'MSE :', mse)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(X.flatten(), y)
plt.scatter(X.flatten(), pred)
plt.title(kernel)
plt.show()




확인해보니 rbf 커널이 가장 좋은 학습 성능을 보여주었다.
- Scikit-Learn -
이번엔 Scikit-Learn을 이용하여 서포트 벡터 머신을 적용해보자.
a. 분류 문제
분류는 SVC 클래스를 이용하여 수행할 수 있다. Scikit-Learn에서 제공하는 커널에 대하여 학습 정확도를 계산해보았다. 참고로 kernel이 'linear'인 경우는 mySVM 클래스에서 커널은 지정하지 않은 경우와 같다.
from sklearn.datasets import load_iris
from sklearn.svm import SVC
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['species'] = [iris.target_names[x] for x in iris.target]
species_to_labels = dict(zip(df['species'].unique(), range(len(df['species'].unique()))))
df['species'] = df['species'].map(species_to_labels)
df = df.rename(columns={'species':'label'})
X = df.drop('label', axis=1).values
y = df['label'].values
for kernel in ['linear', 'poly', 'rbf', 'sigmoid']:
clf = SVC(C=10, kernel=kernel)
clf.fit(X, y)
pred = clf.predict(X)
print('커널 :', kernel, '정확도 :', np.mean(y == pred))

확인해보니 poly인 경우를 제외하고 결과가 동일했다.
b. 회귀 문제
이번엔 보스턴 데이터를 이용하여 회귀를 위한 서포트 벡터 머신을 적용했다. Scikit-Learn에서는 SVR을 이용하여 회귀 SVM을 적용할 수 있다. 이때 mySVM과의 비교를 위하여 Polynomial 커널인 경우에는 차수를 2로 해주었다. 시각화 결과도 추가했다.
from sklearn.datasets import load_boston
from sklearn.svm import SVR
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['y'] = boston.target
X = df[['LSTAT']].values
y = df['y'].values
for kernel in ['linear', 'poly', 'rbf']:
if kernel == 'poly':
reg = SVR(kernel=kernel, C=10, degree=2)
else:
reg = SVR(kernel=kernel, C=10)
reg.fit(X, y)
pred = reg.predict(X)
mse = np.mean(np.square(y-pred))
print('커널 :', kernel, 'MSE :', mse)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(X.flatten(), y)
plt.scatter(X.flatten(), pred)
plt.title(kernel)
plt.show()
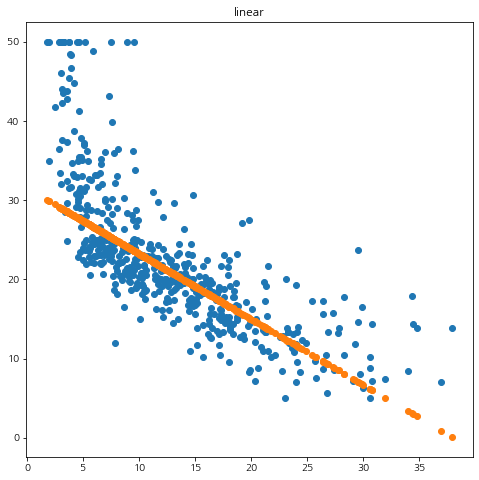

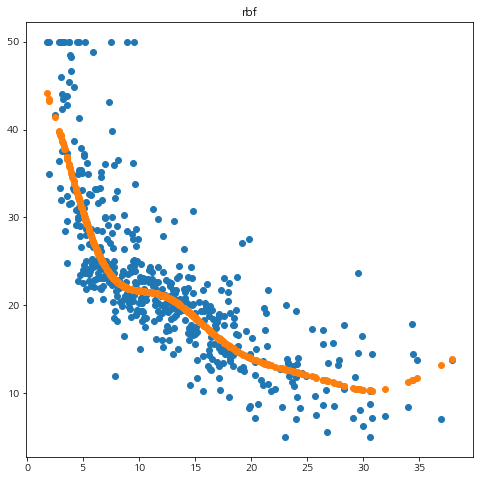
결과는 앞에서 구현한 mySVM과 거의 동일했다. 짝짝~!!
하지만 속도는 Scikit-Learn이 훨씬 빠르다. Scikit-Learn을 쓰자~!!
서포트 벡터 머신 관련 포스팅을 준비하는 것이 의사결정나무를 준비했던 것 다음으로 힘들었다. 구현은 쉬웠으나 수식이 많아서 그렇다. ㄷㄷ;;
그래도 이번 기회를 통해 서포트 벡터 머신에 대한 내용을 가슴 깊이 새긴 거 같아 기분이 좋았다.
참고자료
LIBSVM : A Library for Support Vector Machines
A, J. Smola, B, Scholkopf - A Tutorial on Support Vector Machine
문일철 - 인공지능 및 기계학습 개론 1
Support Vector Machine : Python implementation using CVXOPT

'통계 > 머신러닝' 카테고리의 다른 글
| 21. XGBoost에 대해서 알아보자 (402) | 2022.06.26 |
|---|---|
| 20. Gradient Boosting 알고리즘에 대해서 알아보자 with Python (408) | 2022.06.13 |
| 18. 다중 클래스(Multi-Class) 분류를 위한 One vs Rest, One vs One 방법을 알아보자. (397) | 2022.05.09 |
| 17. Dunn Index와 실루엣(Silhouette) 계수를 이용하여 최적 클러스터(군집, Cluster)개수 정하기 with Python (388) | 2022.05.07 |
| 16. 선형 회귀(Linear Regression) 모형에 대해서 알아보자 with Python (416) | 2022.05.06 |





댓글