이번 포스팅에서는 지도 학습 알고리즘을 통해 만들어진 예측 모형의 성능을 평가하는 지표에 대해서 알아보려고 한다. 성능 지표는 크게 분류 모형과 회귀 모형에 대한 지표로 나눌 수 있다. 여기에서는 분류 모형에 대한 성능 지표로 정분류율(Accuracy), 정밀도(Precision), 민감도(Sensitivity 또는 재현율 Recall)와 특이도(Specificity) 그리고 F1-Score를 알아볼 것이다. 그리고 회귀 모형에 대한 지표는 결정계수(Coefficient of Determination 또는 R Square), 평균 제곱 오차(Mean Square Error : MSE) 그리고 평균 절대 오차(Mean Absolute Error : MAE)에 대해서 알아본다. 그리고 각 성능 지표를 파이썬을 이용하여 구현하는 방법도 소개한다.
- 목차 -
1. 분류 모형 성능 지표
성능 지표를 이야기하기 전에 먼저 학습된 모형 $f$와 정답을 알고 있는 평가 데이터 $(x_i, c_i), i=1, \ldots, n$이라고 해보자. 여기서 $x_i \in \mathbb{R}^p$인 설명 변수 벡터이고 $c_i \in \{ 1, 2, \ldots, K \}$는 범주형 반응 변수이다. 학습된 모형은 $f : \mathbb{R}^p \rightarrow \{ 1, 2, \ldots, K \}$인 함수이다.
1) 정분류율(Accuracy)
a. 정의
정분류율 예측하고자 하는 데이터에서 실제 라벨과 예측 라벨이 일치하는 비율을 의미하며 다음과 같이 계산된다.
$$\text{Accuracy} = \frac{ \text{#}\{ i : f(x_i) = c_i, i = 1, \ldots, n \} }{n}$$
여기서 $\text{#} (A) $은 집합 $A$의 원소 개수이다.
사실 많은 사람들이 정확도라고도 얘기하는데 정분류율이 맞는 표현 같다. 회귀 모형에서도 정확도를 측정할 수 있는 지표가 있으므로 정확도라는 말 자체는 상위 개념이라고 생각한다.
b. 파이썬 구현
위 식을 바탕으로 파이썬으로 정분류율을 계산해보자. 여기서는 분류 데이터에 얼굴 마담이라 할 수 있는 붓꽃데이터를 사용한다. 먼저 데이터를 불러오고 의사결정나무로 학습하고 예측을 수행했다.
import numpy as np
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
## 데이터
iris = load_iris()
X = iris.data
y = iris.target
clf = DecisionTreeClassifier(max_depth=3).fit(X, y) ## 의사결정나무 학습
y_pred = clf.predict(X) ## 예측 라벨
이제 정분류율을 계산하는 함수를 만들어보자. 아래 get_accuracy 함수는 정분류율을 계산한다. 실제 라벨과 예측 라벨이 numpy.array 이므로 논리 연산자를 이용하여 비교한 뒤 평균을 취하면 된다.
def get_accuracy(y_true, y_pred):
acc = np.mean(y_true==y_pred)
return acc
이제 정분류율을 계산해보자.
get_accuracy(y, y_pred)

c. 장단점
정분류율은 라벨(또는 범주)이 어느 정도 균형 있게 분포되어 있을 때 유용하며 범주의 개수와 상관없이 사용할 수 있다. 하지만 불균형 라벨인 경우 정분류율의 사용은 문제가 될 수 있다. 예를 들어 2 분류 문제에서 데이터 100개 중에 95개의 범주는 0 나머지 5개의 범주는 1이라고 할 때 모형의 학습 이런 거 필요 없이 범주를 0으로 예측한다는 규칙을 만든다면 그 성능은 95%가 된다. 따라서 여기에서 1% 올리기 위해 모형을 학습하는 것이 비효율적일 수 있으며 이는 성능 지표를 정분류율로 정했기 때문에 발생할 수 있는 문제이다.
이 경우 정분류율 뿐만 아니라 소수의 범주를 얼마나 잘 맞췄는지도 함께 살펴보는 게 더 합리적일 것이다. 이것이 바로 다음에서 다룰 정밀도(Precision)이다.
2) 정밀도(Precision)
여기서부터 아래에 소개하는 다른 지표들의 경우 2 분류 문제로 가정하며 라벨은 0과 1로 이루어져 있다고 하자. 앞에서 정분류율의 단점을 소개할 때 불균형 범주(Imbalanced Class) 문제에서는 소수의 범주를 얼마나 잘 맞추는 척도가 필요하다고 했다. 이러한 필요에 의해서 나온 것이 바로 정밀도이다.
a. 정의
혼동 행렬
정밀도의 정의를 알아보기 전에 혼동 행렬(Confusion Matrix)을 알아보자. 혼동 행렬은 평가 데이터(정답이 있는 데이터)에 대하여 실제 범주와 예측 범주를 각 카테고리 별로 나누고 해당 카테고리에 들어가는 데이터의 수를 나타낸 행렬이다. 만약 라벨이 총 $K$개라면 혼동 행렬은 $K\times K$가 된다. 여기서는 2 분류 문제를 다룰 것이므로 2 분류 문제에 대한 혼동 행렬을 만들어보는 방법을 알아보자. 먼저 아래와 같이 7개 데이터에 대하여 실제 라벨과 예측 라벨을 얻었다고 해보자.

이제 2개의 칼럼을 각각 예측 라벨 1, 0으로 설정하고 2개의 행을 각각 실제 라벨 1, 0으로 설정한다. 그렇게 되면 4(=2x2)개의 카테고리가 만들어지는데 각 카테고리에 해당하는 데이터 개수를 적는다.

이때 다음을 정의한다.
$$\begin{align} TP &= \text{#} \{ i : f(x_i) = 1 \cap c_i = 1 \} \\ FN &= \text{#} \{ i : f(x_i) = 0 \cap c_i = 1 \} \\
FP &= \text{#} \{ i : f(x_i) = 1 \cap c_i = 0 \} \\
TN &= \text{#} \{ i : f(x_i) = 0 \cap c_i = 0 \} \end{align}$$
정밀도(Precision)는 라벨 1로 예측한 것들 중에서 실제 라벨이 1인 비율을 말하며 다음과 같이 계산할 수 있다.
$$\text{Precision} = \frac{TP}{TP+FP}$$
정밀도는 1에 가까울수록 좋은 분류 모형이라고 판단한다.
b. 파이썬 구현
이제 정밀도를 파이썬으로 구현해 보자. 아래 함수는 정밀도를 계산한다. 예측 라벨이 1인 것들 중에서 실제 라벨도 1인 것들의 비율을 계산한 것이다.
def get_precision(y_true, y_pred):
denom = np.sum(y_pred == 1)
num = np.sum((y_pred == 1)&(y_true==1))
return num/denom
여기서는 2 분류 문제를 다루기 위하여 Scikit-Learn에서 제공하는 유방암 데이터를 갖고 왔다. 이번에도 의사결정나무로 학습시킨 뒤 정밀도를 계산했다.
from sklearn.datasets import load_breast_cancer
# 유방암 데이터
bc = load_breast_cancer()
X = bc.data
y = bc.target
clf = DecisionTreeClassifier(max_depth=5).fit(X, y) ## 의사결정나무 학습
y_pred = clf.predict(X) ## 예측
print(get_precision(y, y_pred)) ## 정밀도 계산

정밀도가 0.99가 나왔다.
c. 장단점
일반적으로 예측이 잘되어야 하는 클래스를 보통 라벨 1로 아닌 것을 0으로 설정하는데 정밀도는 아닌 것(라벨 0)을 맞다고 예측할 때 큰 문제가 발생되는 경우에 사용할 수 있는 지표이다. 예를 들어 스팸이 아닌 것을 스팸이라고 한다면 정말 중요한 메일을 스팸처리하여 읽지 못하게 되고 이는 당사자 입장에서 큰 손실을 야기시킨다. 따라서 스팸 메일을 분류해야 하는 작업(Task)에서는 정밀도가 중요한 성능 지표가 된다. 하지만 정밀도는 맞춰야 하는 것들 중에서 틀린 것이 얼마나 되는지에 대한 정보(TN)를 주지는 않는다.
3) 민감도(Sensitivity)와 특이도(Specificity)
a. 정의
민감도(Sensitivity)는 실제 라벨이 1인 것들 중에서 예측 라벨이 1인 것의 비율을 말한다. 보통 중요하게 생각하는 클래스 라벨을 1로 두는 관행 때문에 민감도는 중요한 클래스를 예측 모형이 중요한 클래스를 얼마나 잘 재현해냈는가 볼 수 있다. 이 때문에 민감도를 재현율(Recall)이라고도 한다. 특이도(Specificity)는 실제 라벨이 0인 것들 중에서 예측 라벨이 0인 것의 비율을 말한다.
민감도와 특이도는 다음과 같이 계산한다.
$$\begin{align} \text{Sensitivity} &= \frac{TP}{TP+FN} \\ \text{Specificity} &= \frac{TN}{TN+FP} \end{align}$$
민감도와 특이도는 모두 클수록 좋은 분류 모형이라고 판단한다.
b. 파이썬 예제
아래 코드는 민감도(get_sensitivity)와 특이도(get_specificity)를 계산하는 함수이다.
def get_sensitivity(y_true, y_pred):
denom = np.sum(y_true == 1)
num = np.sum((y_pred == 1)&(y_true==1))
return num/denom
def get_specificity(y_true, y_pred):
denom = np.sum(y_true == 0)
num = np.sum((y_pred == 0)&(y_true==0))
return num/denom
앞에서 다룬 유방암 데이터를 이용한 예측 모형의 민감도와 특이도를 계산해 보자.
print('민감도', get_sensitivity(y, y_pred))
print('특이도', get_specificity(y, y_pred))

민감도는 1, 특이도는 0.986이 나왔다.
c. 장단점
일반적으로 실제로 맞춰야 하는 클래스(라벨 1)를 맞추지 못할 때 큰 문제가 발생할 수 있는 경우에 사용할 수 있는 지표이다. 예를 들어 암에 걸린 환자(라벨 1)를 아니라고 한 경우 즉, 예측 모형이 맞추지 못한 경우 인명 피해로 이어질 수 있다. 따라서 암환자를 분류해야 하는 작업(Task)에서는 민감도(재현율)가 중요한 성능 지표가 된다. 하지만 민감도(재현율)는 아닌 것(라벨 0)을 맞다고 하는 비율에 대한 정보는 제공하지 않는다.
민감도(재현율)와 정밀도 차이
민감도(재현율)와 정밀도 모두 분자에 TP가 들어가지만 분모가 다르다는 차이가 있다. 이는 보고자 하는 것이 다르기 때문이다. 예를 들어 스팸 메일을 분류하는 것에서는 정밀도가 좋다고 했다. 그 이유는 스팸이 아닌 것을 스팸이라고 예측하는 경우와 스팸인 것을 스팸이라고 예측 하는 경우를 비교해보면 알 수 있다. 전자에 대한 대가는 (사람들은 보통 스팸 메일을 읽어볼 시도조차 안한다는 점을 감안하면) 해당 메일이 중요한 사업에 대한 메일인 경우 개인적으로는 회사에서 짤리는 것과 회사 입장에서 큰 영업 손실이다. 후자는 메일 몇줄 읽어보는 시간과 클릭을 좀 더하는 수고일 것이다. 당연히 전자가 더 큰 손실이며 스팸 메일 분류 문제에서는 스팸이 아닌 것을 스팸이라고 예측 하는 경우를 줄이고자 민감도보다는 정밀도를 성능 지표로 사용한다.
반대로 암 환자 분류의 경우 암 환자를 아니라고 한 경우가 암이 아닌 환자를 암이라고 진단하는 경우보다 더 큰 손실이므로 암 환자 분류 문제에서는 정밀도보다는 민감도를 성능 지표로 사용한다.
4) F1-Score
a. 정의
F1-Score는 정밀도(Precision)와 재현율(Recall, 민감도)의 조화 평균으로 다음과 같이 계산한다.
$$\text{F1-Score} = \frac{2\cdot \text{Precision} \cdot \text{Recall}}{\text{Precision} + \text{Recall}}$$
F1-Score는 0과 1사이의 값을 가지며 1에 가까울수록 좋은 분류 모형이라고 판단한다.
F1-Score의 고찰
불균형 클래스(Imbalanced Class) 자료에 대해서 머신러닝 분류 모형의 성능을 측정하는 데에는 정분류율보다는 정밀도 또는 재현율이 더 좋은 지표가 될 수 있다. 그렇다면 정밀도와 재현율을 각 문제에 대해서 따로 사용할 것인가에 대한 의문이 든다. 둘 다 좋은 지표이므로 분류 모형 성능을 체크할 때 정밀도, 재현율 모두 계산해서 값을 비교해 볼 수도 있겠지만 이는 두 가지 지표를 매번 봐야 하므로 귀찮은 일이다.
그래서 사람들은 생각했다.
하나의 값을 이용하여 정밀도와 재현율을 컨트롤할 수는 없는지..
있다!!
그것이 바로 F1-Score이다. F1-Score는 0과 1 사이 값을 갖는데 1에 가까울수록 정밀도와 재현율이 일반적으로 모두 높아진다. 즉, F1-Score 값이 높은 모형이 정밀도와 재현율이 모두 높아지게 하는 모형이라는 것이다. 그 이유를 살펴보자. $0\leq x \leq 1, 0\leq, y \leq 1$일 때 $x, y$의 조화평균 $z$는 다음과 같다.
$$z = 2xy/(x+y) \tag{1}$$
아래 그림은 $z$에 대한 등고선도를 그린 것이다.
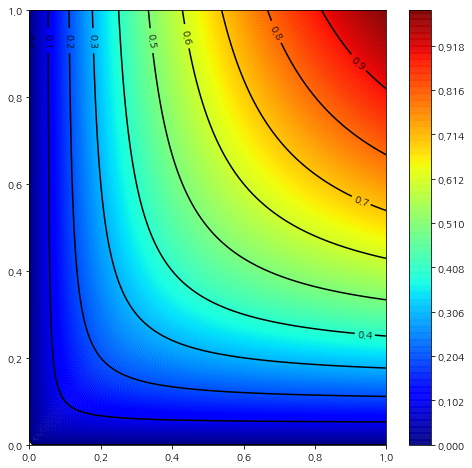
위 그림에서 $z$값이 커질수록 이에 대응하는 $x, y$의 최소값이 동시에 커지는 것을 알 수 있다. 예를 들어 아래 그림과 같이 $z=0.6$인 경우의 $x, y$가 가질 수 있는 최소값은 대략 0.4인 반면 $z=0.9$에서 $x, y$의 최소값은 대략 0.8인 것을 알 수 있다.

이는 수식으로도 증명할 수 있다. 먼저 $z$를 상수로 간주하고 (1)을 $x$에 대해서 정리하면 다음과 같다.
$$x = \frac{yz}{2y-z}$$
이때 $dx/dy = -z^2/(2y-z)^2$이므로 $x$는 $y$에 대한 감소함수가 되고 $x$의 $y$의 최대값인 1일 때 최소값을 갖는다. 따라서
$$x_{\text{min}} = \frac{z}{2-z}\tag{2}$$
이다. (2)는 $x_{\text{min}}$은 $(0, 1)$에서 $z$에 대한 증가함수이므로 $z$가 커질 수록 $x_{\text{min}}$은 증가한다. $y$의 최소값이 증가하는 것도 위와 비슷하게 증명할 수 있다.
결론적으로 F1-Score($z$)가 커지면 정밀도($x$)와 재현율($y$)이 모두 커질 가능성이 높다는 것을 알 수 있다.
반대로 어떤 분류 모형의 F1-Score가 0에 가까워지면 정밀도 또는 재현율 값이 낮다. 따라서 정밀도, 재현율이 모두 높은 상황이 아니므로 해당 모형은 그다지 좋지는 않은 것이다.
b. 파이썬 예제
아래 코드는 F1-Score를 이용하여 계산하는 함수이다. 앞에서 소개한 정밀도와 재현율을 계산하는 함수를 사용했다.
def get_f1_score(y_true, y_pred):
precision = get_precision(y_true, y_pred)
sensitivity = get_sensitivity(y_true, y_pred)
value = 2*precision*sensitivity/(precision+sensitivity)
return value
앞에서 다룬 유방암 데이터를 이용한 예측 모형의 F1-Score를 계산해 보자.
print(get_f1_score(y, y_pred))

0.9958이 나왔다.
c. 장단점
F1-Score는 정밀도와 재현율처럼 불균형 클래스 자료에 대해서 사용해 볼 수 있는 지표이며 하나의 값으로 정밀도와 재현율 두 가지 값을 컨트롤할 수 있다는 장점이 있다. 하지만 F1-Score는 그 값이 높다면 정밀도와 재현율이 높을 수 있다는 해석을 할 수 있는데 그 값이 낮다면 정밀도만 낮은지 재현율만 낮은지 아니면 둘 다 낮은지에 대한 해석이 어렵다는 단점이 있다.
2. 회귀 모형 성능 지표
학습된 모형 $f$와 정답을 알고 있는 평가 데이터 $(x_i, y_i), i=1, \ldots, n$이라고 해보자. 여기서 $x_i \in \mathbb{R}^p$인 설명 변수 벡터이고 $y_i \in \mathbb{R}$은 실수이다. 학습된 모형은 $f : \mathbb{R}^p \rightarrow \mathbb{R}$인 함수이다.
1) 결정계수(Coeffcient of Determination, R Square)
a. 정의
결정계수(Coeffcient of Determination, R Square) $R^2$는 다음과 같이 계산된다.
$$R^2 = 1-\frac{SSE}{SST}\tag{3}$$
여기서
$$SSE = \sum_{i=1}^n (y_i-f(x_i))^2, SST = \sum_{i=1}^n(y_i-\bar{y})^2, \bar{y} = \sum_{i=1}^ny_i/n$$
결정 계수는 항상 1보다 작거나 같다.
결정계수는 $f$가 어떤 모형인지에 따라서 그 의미가 달라진다. $f$가 절편이 있는 선형 회귀 모형인 경우에는 결정계수를 총 변동 대비 모형이 설명할 수 있는 변동 비율로 해석한다. 왜 그런지 살펴보자.
먼저 $SSR=\sum_{i=1}^n(f(x_i)-\bar{y})^2$이라 하자. 절편이 있는 회귀 모형인 경우에는 다음과 같이 총 변동 $SST$가 모형으로 설명할 수 없는 변동 $SSE$와 모형으로 설명할 수 있는 변동 $SSR$로 정확하게 분해가 된다(증명은 여기를 참고하기 바란다).
$$SST = SSR+SSE$$
따라서 (3)은 다음과 같이 쓸 수 있다.
$$R^2 = \frac{SST-SSE}{SST} = \frac{SSR}{SST}\tag{4}$$
$SST$의 분해 성질과 각각의 제곱합은 양수이므로 (4)는 0보다 작아질 수 없으며 그에 따라 결정계수는 0과 1 사이에 값을 갖게 된다. 따라서 비율로 해석할 수 있는 것이다.
만약 $f$가 비선형 모형(의사결정 나무, 서포트 벡터 머신 등)이거나 절편이 없는 회귀 모형의 경우에는 결정계수를 위와 같은 비율로 해석할 수 없다(왜냐하면 음수가 될 수도 있기 때문이다). 이때 결정 계수는 기본(Base) 모형인 $g(x_i) = \bar{y}, i=1, \ldots, n$의 오차 제곱 대비 모형 $f$의 잔차 제곱 비를 1에서 빼준 것이며 그 값이 클수록 좋고 작을수록 안 좋다. 이때에는 $R^2$보다는 $1-R^2 = SSE/SST$를 지표로 쓰는 게 더 자연스러워 보인다. 이렇게 쓰면 그 값이 작을수록 좋은 것이며 기본 모형의 오차 제곱대비 학습한 모형의 오차제곱 비로 바로 해석할 수 있기 때문이다.
b. 파이썬 예제
아래 코드는 결정계수를 계산하는 함수이다.
def get_r_square(y_true, y_pred):
denominator = np.sum(np.square(y_true-np.mean(y_true)))
numerator = np.sum(np.square(y_true-y_pred))
return numerator/denominator
이번엔 실제 데이터를 이용하여 회귀모형을 학습하고 결정계수를 계산해 보자. 여기서는 보스턴 집값 데이터를 이용했으며 회귀 모형으로는 의사결정나무를 사용했다.
from sklearn.datasets import load_boston
from sklearn.tree import DecisionTreeRegressor
boston = load_boston()
X = boston.data
y = boston.target
reg = DecisionTreeRegressor(max_depth=3).fit(X, y)
y_pred = reg.predict(X)
print(get_r_square(y, y_pred))

결정계수가 0.8178 정도가 나왔다.
c. 장단점
결정계수는 그 자체로 모형의 성능을 나타낼 수 있을 뿐 아니라 기본 모형(평균으로 예측하는 것) 대비 학습 모형의 성능을 비교할 수 있다는 점에서 유용하다. 하지만 선형 회귀 모형의 경우 설명 변수를 추가하면 결정계수가 커지므로 아무 변수가 막 들어간 모형을 선택할 수 있게 된다. 이를 보정하기 위해 수정된 결정계수(Adjusted R Sqaure)를 사용하기도 한다.
2) 평균 제곱 오차(Mean Squared Error : MSE)
a. 정의
평균 제곱 오차(Mean Squared Error : MSE)는 실제값 $y_i$와 모형 예측값 $f(x_i)$간의 차이 즉, 오차를 측정하는 방법이며 다음과 같이 계산한다.
$$\text{MSE} = \frac{1}{n} \sum_{i=1}^n(y_i-f(x_i))^2$$
평균 제곱 오차는 실제값과 모형 예측값 사이의 거리로 볼 수 있는데 그 값이 작을수록 모형의 성능이 좋다고 할 수 있다.
b. 파이썬 예제
아래 코드는 MSE를 계산하는 코드이다.
def get_mse(y_true, y_pred):
value = np.mean(np.square(y_true-y_pred))
return value
앞에서 다룬 보스턴 집값 데이터에 대한 의사결정나무의 MSE는 다음과 같다.
print(get_mse(y, y_pred))

c. 장단점
평균 제곱 오차(MSE)는 실제값과 예측값 사이의 거리라는 기하학적 해석이 가능하다. 또한 평균 제곱 오차를 비용함수로 사용한다면 최적화 문제를 쉽게 풀 수 있다. 하지만 평균 제곱 오차는 이상치에 민감하게 반응하므로 이상치에 과도하게 쏠리는 모형을 선택할 수 있다는 단점이 있다.
3) 평균 절대 오차(Mean Absolute Error : MAE)
a. 정의
평균 절대 오차(Mean Absolute Error) 또한 평균 제곱 오차와 마찬가지로 오차를 측정하는 하나의 방법이며 다음과 같이 계산한다.
$$\text{MAE} = \frac{1}{n}\sum_{i=1}^n|y_i-f(x_i)|$$
b. 파이썬 예제
아래 코드는 평균 절대 오차(MAE)를 계산하는 코드이다.
def get_mae(y_true, y_pred):
value = np.mean(np.abs(y_true-y_pred))
return value
보스턴 집값 데이터를 이용한 의사결정나무의 평균 절대 오차를 계산해 보자.
print(get_mae(y, y_pred))

c. 장단점
평균 절대 오차(MAE) 또한 평균 제곱 오차와 마찬가지로 실제값과 예측값 사이의 거리라는 기하학적인 해석이 가능하며 이상치에 민감하지 않은 모형을 선택할 수 있다는 장점이 있다. 하지만 비용 함수(또는 목적 함수)로 사용할 경우 최적화하기가 어렵다.
'통계 > 머신러닝' 카테고리의 다른 글
| 33. 클러스터링(군집화) 평가 지표 Calinski-Harabasz index, Davies-Bouldin index, Rand Index에 대해서 알아보자 with Python (1) | 2023.01.22 |
|---|---|
| 32. Gain Chart와 Lift Chart에 대해서 알아보자 with Python (0) | 2023.01.17 |
| 30. DBSCAN에 대해서 알아보자 with Python (0) | 2022.11.03 |
| 29. Piecewise Polynomial(Constant, Linear) Regression에 대해서 알아보자 with Python (6) | 2022.10.20 |
| 28. K-Modes Clustering(클러스터링, 군집화)에 대해서 알아보자 with Python (383) | 2022.09.04 |





댓글