안녕하세요~ 꽁냥이에요!!
선형 회귀 모형의 가정 중에는 오차의 등분산성이 있어요. 오차의 등분산성이란 오차의 분산이 회귀 모형에 포함된 설명 변수의 값과 상관없이 일정하다는 뜻입니다.
오차의 등분산성을 확인해보는 방법은 설명 변수와 잔차의 산포를 나타내는 잔차도를 그려서 시각적으로 확인해보는 방법이 있는데요. 통계적 검정방법을 이용하는 방법도 있습니다. 잔차도를 그리는 방법은 여기를 참고하세요.
이번 포스팅에서는 통계적인 검정 방법을 이용하여 오차의 등분산성을 확인하는 방법을 소개합니다. 여기서는 아래의 2가지 검정 방법을 소개합니다.
1. Brown-Forsythe 검정
오차(Error)의 등분산성을 확인한다는 것은 (모형에 사용된) 설명 변수 값에 따라 오차의 분산이 변하지 않는다는 가정을 확인한다는 것입니다. 잔차(Residual)는 오차의 정보를 갖고 있는데요. 특히 오차의 분산에 대한 정보는 잔차의 제곱 또는 잔차의 절대값을 이용하여 확인합니다. 이때 설명 변수를 기준으로 데이터를 두개(샘플 수가 많다면 세개 이상)의 그룹으로 나누고 각 그룹별로 잔차 편차(잔차 - 그룹별 잔차 중앙값)의 평균을 구합니다. 이 때 그룹별로 평균의 차이가 없다면 이는 설명 변수에 따라 오차의 분산이 변하지 않는다고 할 수 있을 것입니다. 이것이 Brown-Forsythe 검정의 아이디어입니다.
지금 꽁냥이에게 서로 독립인 데이터 $(x_i, y_i), \:\: i=1, 2, \cdots, n$ 가 있다고 해볼게요. 즉, 반응 변수 한 개, 설명 변수 한 개이고 데이터는 $n$개가 있는 상황이지요. Brown-Fosythe의 검정 방법은 다음과 같습니다.
1) 선형 모형을 적합한다.
2) 적합한 선형 모형을 이용하여 잔차를 구한다.
3) 적합에 사용한 설명 변수를 이용하여 잔차를 두 그룹으로 나눈다.
4) 각 그룹에서 잔차의 중간값을 구하고 잔차와 중간값 차이의 평균을 구한다.
5) 두 그룹에서 계산한 차이를 이용하여 이 표본(Two sample) t 테스트를 수행한다.
위의 과정을 좀 더 구체적으로 살펴보겠습니다.
1) 선형 모형을 적합한다.
설명 변수와 반응 변수의 기대값이 다음과 같은 관계를 갖는다고 한다면
$$E(y_i) = \beta_0+\beta_1 x_i, \:\: i=1, 2, \cdots, n$$
최소제곱법을 이용하여 $\beta_0$와 $\beta_1$를 추정합니다. $\beta_0$와 $\beta_1$의 최소제곱추정량을 각각 $b_0$, $b_1$ 라고 하겠습니다.
2) 적합한 선형 모형을 이용하여 잔차를 구한다.
추정된 회귀 직선을 이용하여 잔차를 구합니다. 잔차 $e_i\:(i=1, \cdots, n)$는 다음과 같이 구합니다.
$$e_i=y_i-\hat{y}_i$$
여기서 $\hat{y}_i=b_0+b_1x_i$입니다.
3) 적합에 사용한 설명 변수를 이용하여 잔차를 두 그룹으로 나눈다.
예를 들어 $x_i$가 사람의 키라면 160cm를 기준으로 두 그룹으로 나누거나 성별이라면 남자 여자를 기준으로 두 그룹을 나누는 것을 말합니다. 여기서 두 그룹의 데이터 개수가 서로 비슷하도록 기준을 나누도록 합니다.
4) 각 그룹에서 잔차의 중간값을 구하고 잔차와 중간값 차이의 평균을 구한다.
첫 번째 그룹의 잔차를 $e_{i1}, (i=1, \cdots, n_1)$, 잔차의 중간값을 $\tilde{e}_1$, 그리고 두 번째 그룹의 잔차를 $e_{i2}, (i=1, \cdots, n_2)$, 잔차의 중간값을 $\tilde{e}_2$라 하겠습니다. 여기서 $n_1, n_2$는 각각 첫 번째, 두 번째 그룹의 데이터 개수입니다. 잔차의 평균이 아닌 중간값을 사용한 이유는 이상치에 영향을 받지 않기 위함입니다.
그러고 나서 다음과 같이 각 그룹별로 잔차와 중간값의 차이를 계산합니다.
$$d_{i1} = |e_{i1}-\tilde{e}_1|, d_{i2} = |e_{i2}-\tilde{e}_2|$$
여기서 $d_{i1}, d_{i2}$는 각각 첫 번째, 두 번째 그룹의 잔차와 중간값의 차이입니다.
마지막으로 그룹별로 차이의 평균을 다음과 같이 구합니다.
$$\bar{d}_j=\frac{1}{n_j}\sum_{i=1}^{n_j}d_{ij}, \:\: j=1,2$$
5) 두 그룹에서 계산한 차이를 이용하여 이 표본(Two sample) t 테스트를 수행한다.
테스트를 수행하기 위해서 다음과 같이 검정 통계량 $t_{BF}$을 구합니다.
$$t_{BF}=\frac{\bar{d}_1-\bar{d}_2}{s\sqrt{\frac{1}{n_1}+\frac{1}{n_2}}}$$
여기서
$$s^2=\frac{\sum(d_{i1}-\bar{d}_1)^2+\sum(d_{i2}-\bar{d}_2)^2}{n-2}$$
이렇게 구한 $t_{BF}$가 근사적으로 자유도가 $n-2$인 t 분포를 따른다는 사실을 이용하여 테스트를 수행합니다. 두 그룹에서 계산한 $t_{BF}$의 값이 유의미하게 작다면 두 그룹의 차이는 없다고 판단할 수 있고 이는 다시 오차의 등분산성이 위배되지 않는다고 판단할 수 있습니다.
이제 파이썬을 이용하여 Brown-Forsythe 검정을 수행하겠습니다. 여기에서 사용할 데이터를 첨부할 테니 다운받아 주세요.
먼저 필요한 모듈을 임포트하고 데이터를 불러옵니다.
import pandas as pd
import numpy as np
from scipy.stats import t
from statsmodels.formula.api import ols
df = pd.read_csv('toluca_company_dataset.csv') ## 데이터 불러오기

이제 검정 통계량을 계산할 차례입니다.
fit = ols('Work_hours ~ Lot_size',data=df).fit() ## 단순선형회귀모형 적합
## 그룹별 잔차를 구한다.
def get_median(x):
## 중간값을 계산하는 함수
x = sorted(x)
mid_index = len(x)//2
return (x[mid_index]+x[~mid_index])/2
median_lot_size = get_median(df['Lot_size']) ## Lot_size의 중앙값
g1 = [i for i in df['Lot_size'].index if df['Lot_size'][i] <= median_lot_size] ## 중간값이하의 데이터는 그룹 1로 한다.
g2 = [i for i in df['Lot_size'].index if df['Lot_size'][i] > median_lot_size] ## 중간값을 초과하는 데이터는 값은 그룹 2로한다.
e1 = [] ## 그룹 1의 잔차
e2 = [] ## 그룹 2의 잔차
for i in df['Lot_size'].index:
fitted_value = fit.params.Intercept + fit.params.Lot_size*df['Lot_size'][i] ## 해당 Lot_size에 대한 Work_hours의 추정값
resid = df['Work_hours'][i] - fitted_value ## 잔차
if i in g1:
e1.append(resid)
else:
e2.append(resid)
median_e1 = get_median(e1) ## 그룹 1 잔차 중앙값
median_e2 = get_median(e2) ## 그룹 2 잔차 중앙값
d1 = [] ## 그룹 1 잔차와 잔차 중앙값의 차이
d2 = [] ## 그룹 2 잔차와 잔차 중앙값의 차이
for e in e1:
d1.append(abs(e-median_e1))
for e in e2:
d2.append(abs(e-median_e2))
## 검정통계량 계산
pooled_var_num = sum([(x-np.mean(d1))**2 for x in d1]) + sum([(x-np.mean(d2))**2 for x in d2])
pooled_var_denom = len(df)-2 ## 자유도
pooled_var = pooled_var_num/pooled_var_denom ## pooled variance
s = np.sqrt(pooled_var) ## standard deviation of pooled variance
t_bf = (np.mean(d1)-np.mean(d2))/(s*np.sqrt(1/len(d1)+1/len(d2))) ## 검정 통계량
line 1
설명 변수를 Lot_size, 반응 변수를 Work_hours로 하는 단순 선형 회귀모형을 적합시켜줍니다. 이에 대한 설명은 여기를 참고하세요.
line 5~9
중앙값을 자주 사용하기 때문에 중앙값을 구해주는 함수를 따로 만들어주었습니다.
line 13~14
Lot_size 데이터를 Lot_size의 중앙값 보다 작거나 같은쪽은 그룹1에 큰쪽은 그룹2에 할당하였습니다.
line 16~24
적합한 모형의 회귀계수를 이용하여 각 그룹별 잔차를 구해줍니다.
line 26~27
그룹별 잔차들의 중앙값을 구합니다.
line 29~34
그룹별 잔차와 중앙값의 차이를 구합니다.
line 37~42
검정 통계량을 구합니다.
위 코드를 실행하고 검정 통계량의 값이 얼마인지 확인합니다.
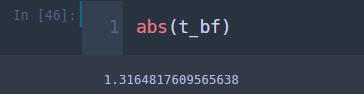
양측 검정을 수행할 것이므로 검정 통계량의 절대값을 보아야합니다. 그리고 유의수준 5%에서 자유도가 23(=25-2)인 t 분포의 왼쪽 꼬리확률이 0.025에 해당하는 값(절대값)을 구합니다.
## 기각역
alpha = 0.05 ## 유의수준
critical_value = t.ppf(1-alpha/2,len(df)-2) ## 2.069
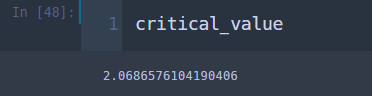
검정 통계량 값 1.316이 꼬리 값 2.069보다 작으므로 귀무가설을 기각할 수 없습니다. 즉, 두 그룹의 평균의 차이가 없다고 할 수 있으며 이는 설명 변수에 따라 분산이 변하지 않는다는 뜻입니다. 즉, 오차의 등분산성을 위배하지 않는다고 결론을 내릴 수 있습니다.
2. Breusch-Pagan 검정
잔차와 설명 변수 또는 잔차의 절대값과 설명변수의 산포도를 그려보았더니 다음과 같은 형태가 나왔다고 해볼게요.

보시는 바와 같이 설명 변수의 값이 증가함에 따라 잔차의 변동성도 증가하는 것을 확인할 수 있습니다. 여기서 잔차의 제곱 값 $e_i^2$을 반응 변수로 두고 설명 변수는 그대로 $x_i$로 하여 선형 모형을 적합하는 것을 생각해볼 수 있습니다. 다음과 같이 말이죠.
$$e_i^2=\gamma_0+\gamma_1x_i, \:\:i=1, 2, \cdots, n\tag{1}$$
여기서 귀무가설 $H_0 : \gamma_1 = 0$을 테스트하여 기각할 수 있다면 이는 오차의 분산이 설명 변수에 따라 증가(또는 감소)한다고 말할 수 있고 이는 오차의 등분산성에 위배된다고 말할 수 있지요. 이것이 Breusch-Pagan 검정의 기본 아이디어입니다.
Breusch-Pagan 검정을 위하여 다음과 같은 가정을 하고 있습니다.
1) 샘플 수가 많아야 할 것
2) 오차항은 독립이고 정규분포를 따라야 할 것
3) 오차의 분산은 설명 변수와 연관이 있어야 할 것
다음으로 Breusch-Pagan 검정 과정을 알아보겠습니다. 먼저 (1)식에 대한 회귀제곱합을 $SSR^*$라고 합시다. 즉,
$$SSR^*=\sum_{i=1}^{n}(\hat{\gamma}_0+\hat{\gamma}_1x_i-\overline{e_i^2} )^2$$
그리고 $SSE$는 잔차제곱합으로 아래와 같습니다.
$$SSE=\sum_{i=1}^{n}e_i^2$$
이제 Breusch-Pagan 검정 통계량 $\chi_{BF}^2$은 다음과 같이 정의합니다.
$$\chi_{BF}^2=\frac{SSR^*}{2}\div\left(\frac{SSE}{n}\right)^2$$
이때 샘플의 개수가 충분(보통 20개 이상)하고 귀무가설 $H_0 : \gamma_1 = 0$이 참일 때 $\chi_{BF}^2$은 근사적으로 자유도가 1인 카이제곱 분포를 따른다고 알려져 있습니다. $\chi_{BF}^2$ 값이 유의미하게 크다면 귀무가설을 기각하게 되고 이는 오차의 등분산성 가정이 위배된다고 결론 내릴 수 있습니다.
이제 말로만 하면 슬슬 지겨울 것 같으니 코드로 구현해볼까요? 데이터와 필요한 모듈을 임포트 하겠습니다.
import pandas as pd
import numpy as np
from scipy.stats import chi2
from statsmodels.formula.api import ols
df = pd.read_csv('toluca_company_dataset.csv') ## 데이터 불러오기
다음으로 Breusch-Pagan 검정을 수행하는 코드를 살펴볼게요.
fit = ols('Work_hours ~ Lot_size',data=df).fit() ## 단순선형회귀모형 적합
sse = sum(np.square(fit.resid)) ## 잔차 제곱합
res_square = np.square(fit.resid) ## 잔차 제곱
## 잔차 제곱과 Lot_size사이의 회귀적합을 위한 데이터프래임 생성
df_res = pd.DataFrame()
df_res['Lot_size'] = df['Lot_size']
df_res['Res_square'] = res_square
fit_res = ols('Res_square ~ Lot_size',data=df_res).fit() ## 잔차 제곱과 Lot_size 단순선형회귀모형 적합
mean_rs = np.mean(res_square) ## 잔차 제곱의 평균
fitted_val = fit_res.params.Intercept + fit_res.params.Lot_size * df_res['Lot_size']
ssr_star = sum(np.square(fitted_val-mean_lrs)) ## 회귀제곱합
## 검정통계량
num = ssr_star/2
denom = np.square(sse/len(df))
chi_bp = num/denom ## 검정통계량
line 1
설명 변수를 Lot_size, 반응 변수를 Work_hours로 하는 단순선형회귀모형을 적합시켜줍니다.
line 3~4
잔차 제곱합과 잔차 제곱 벡터를 만들어줍니다.
line 7~9
잔차 제곱과 Lot_size을 열로 갖는 데이터프래임을 생성합니다.
line 11
잔차 제곱을 반응 변수로 Lot_size를 설명 변수로 하는 단순선형회귀모형을 적합합니다.
line 13~15
잔차 제곱의 평균과 line 11에 구한 회귀계수를 이용하여 회귀제곱합을 계산합니다.
line 18~21
검정 통계량을 계산합니다.
위 코드를 실행하고 검정 통계량의 값을 확인합니다.

검정 통계량의 값이 약 0.821입니다. 다음으로 유의수준을 5%로 설정하고 오른쪽 꼬리 확률 0.05에 해당하는 값을 구합니다.
## 기각역
alpha = 0.05 ## 유의수준
critical_value = chi2.ppf(1-alpha,1) ## 기각값

검정 통계량 값 0.821은 유의수준 5%에 해당하는 기각값 3.841 보다 작으므로 귀무가설 $H_0$를 채택합니다. 따라서 설명 변수가 증가함에 따라 오차의 분산이 증가한다고 할 수 없으며 이는 오차의 등분산성 가정을 위배하지 않는다라고 결론 내리게 됩니다.
Brown-Forsythe 검정의 장점은 오차의 정규성에 크게 영향을 받지 않는(Robustness) 장점이 있지만 그룹별 샘플의 수가 충분히 크지 않다면 테스트의 결과를 신뢰할 수 없다고 알려져 있습니다.
Breusch-Pagan 검정의 경우 여기서는 설명 변수와 잔차의 제곱의 관계를 선형으로 한정했지만 다른 여러 모형으로 확장할 수 있으므로 다양하게 오차의 등분산성을 확인할 수 있습니다. 하지만 오차의 정규성에 민감하다고 알려져 있습니다.
그래서 어떤 걸 써야 할까?
오차의 등분산성 가정을 테스트하는 방법은 우선 잔차도와 앞에서 소개한 2가지 테스트를 사용하여 다각적으로 확인해보시기 바랍니다. 만약 2가지 테스트 중에서 하나를 골라야 한다면 꽁냥이는 개인적으로 Brown-Forsythe 검정 방법을 추천합니다. 왜냐하면 Breusch-Pagan 검정의 경우 오차의 분포가 정규분포가 아니면 사용하기 어렵기 때문입니다.
앞에서 소개한 방법 이외에도 오차의 등분산성 가정을 테스트하는 방법이 많이 있는데요. 여기를 참고하시면 되겠습니다.
'데이터 분석 > 데이터 분석' 카테고리의 다른 글
| [회귀 분석] 6. 변수 선택법(Variable Selection) with Python (10) | 2020.10.01 |
|---|---|
| [회귀 분석] 5. 최적 모형 선택(All possible search 또는 Best subsets algorithm) with Python (7) | 2020.09.26 |
| [회귀 분석] 3. 정규분포에 대한 가정 검정하기 with Python (2) | 2020.09.19 |
| [회귀 분석] 2. 잔차도(Residual plot)와 QQ plot 그리기 (0) | 2020.09.18 |
| [회귀 분석] 1. Python을 이용하여 단순 선형 회귀 모형 적합해보기! (0) | 2020.09.14 |





댓글