안녕하세요~ 꽁냥이에요!
수많은 변수 중에서 관심의 대상이 되는 변수(반응 변수)를 잘 설명하는 변수를 골라서 회귀 모형을 구축한다면 좋은 모형이 될 수 있을 거예요. 이번 포스팅에서는 변수 선택 방법에 대해서 소개하고 파이썬을 이용하여 구현해보겠습니다. 여기서 다루는 내용은 다음과 같습니다.
3. 후진 소거법(Backward Elimination)
4. 단계별 선택법(Forward Stepwise Selection)
1. 데이터 준비
이번 포스팅에서 사용할 데이터를 다운받아주세요.
필요한 모듈을 임포트하고 데이터를 불러옵시다~!!
import pandas as pd
import statsmodels.api as sm
import matplotlib.pyplot as plt
df = pd.read_csv('./surgical_unit.csv') ## 데이터 불러오기
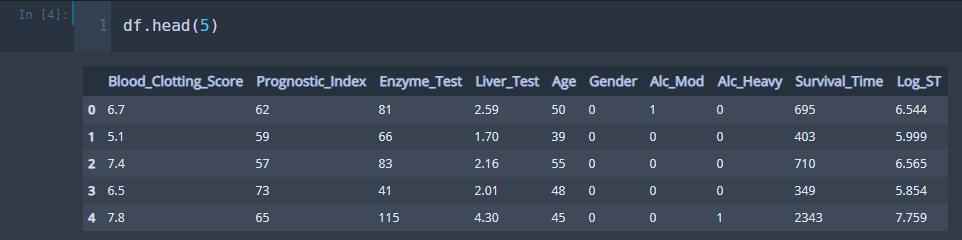
여기서 Log_ST 변수는 쓰지 않습니다.
2. 전진 선택법(Forward Selection)
전진 선택법은 기존 모형에 가장 설명력이 좋은 변수를 하나씩 추가하는 방법입니다. 전진 선택법에서는 변수를 추가할지 말지 결정하는 유의수준을 정하는데요. 가장 설명력이 좋은 변수라 하더라도 이 유의수준을 만족하지 못하면 선택이 되지 않고 전진 선택 알고리즘은 끝나게 됩니다. 구체적으로 살펴보겠습니다.
먼저 $S$는 기존 모형에 포함된 변수들의 집합, $\tilde{S}$를 모형에 포함되지 않은 변수들의 집합이라고 하겠습니다. 그리고 유의수준을 $\alpha$라 하겠습니다.
1 단계) 아직 모형의 적합시키지 않은 변수 $X_k \in \tilde{S}$를 기존 모형에 추가하여 적합합니다. 기존 모형에 추가하여 적합한다는 말은 기존 모형의 있었던 변수와 추가된 변수 $X_k$를 이용하여 선형 모형을 적합한다는 뜻입니다.
2 단계) 변수 $X_k$에 대한 회귀 계수 $b_k$를 구하고 $b_k$에 대한 $t$ 통계량을 계산합니다. 그리고 $t$ 통계량에 대응하는 p-value를 구합니다. 이 작업을 $\tilde{X}$에 있는 모든 변수에 대해서 수행합니다.
이때 $t$ 통계량은 다음과 같이 계산합니다.
$$t = \left(\frac{SSR(X_k \cup S) - SSR(S)}{1} \div \frac{SSE(X_k \cup S)}{n-card (S)-1} \right)^{\frac{1}{2}}$$
여기서 $SSR(A)$, $SSE(A)$는 각각 집합 $A$에 포함된 모든 변수를 포함한 선형 모형의 회귀 제곱합, 잔차 제곱합이며 $card(A)$는 집합 $A$의 변수 개수입니다. 또한 $t$ 통계량은 자유도가 $n-card (S)-1$인 $t$ 분포를 따르므로 $p$-value는 다음과 같이 구합니다.
$p$-value $= P(T > t)$
여기서 $T$는 자유도가 $n-card (S)-1$인 $t$ 분포를 따르는 확률 변수입니다.
3 단계) 이때 최소 $p$-value 값과 미리 정해둔 유의수준 $\alpha$와 비교합니다. 만약 최소 $p$-value < $\alpha$이면 최소 $p$-value에 해당하는 변수를 $S$에 포함시키고 1~2단계를 수행합니다. 그렇지 않은 경우에는 알고리즘을 종료합니다.
아래 코드는 전진 선택법을 구현한 코드입니다.
## 전진 선택법
variables = df.columns[:-2].tolist() ## 설명 변수 리스트
y = df['Survival_Time'] ## 반응 변수
selected_variables = [] ## 선택된 변수들
sl_enter = 0.05
sv_per_step = [] ## 각 스텝별로 선택된 변수들
adjusted_r_squared = [] ## 각 스텝별 수정된 결정계수
steps = [] ## 스텝
step = 0
while len(variables) > 0:
remainder = list(set(variables) - set(selected_variables))
pval = pd.Series(index=remainder) ## 변수의 p-value
## 기존에 포함된 변수와 새로운 변수 하나씩 돌아가면서
## 선형 모형을 적합한다.
for col in remainder:
X = df[selected_variables+[col]]
X = sm.add_constant(X)
model = sm.OLS(y,X).fit()
pval[col] = model.pvalues[col]
min_pval = pval.min()
if min_pval < sl_enter: ## 최소 p-value 값이 기준 값보다 작으면 포함
selected_variables.append(pval.idxmin())
step += 1
steps.append(step)
adj_r_squared = sm.OLS(y,sm.add_constant(df[selected_variables])).fit().rsquared_adj
adjusted_r_squared.append(adj_r_squared)
sv_per_step.append(selected_variables.copy())
else:
break
line 20~21
전진 선택법을 구현할 때에는 $t$ 통계량을 직접 구하지 않고 statsmodels에서 제공하는 pvalues를 이용하여 $p$-value만 구하면 됩니다.
위 코드를 실행하고 최종적으로 선택된 변수들이 어떤 것이 있는지 살펴보겠습니다.

전진 선택법을 적용한 결과 'Liver_Test', 'Alc_Heavy', 'Enzyme_Test', 'Prognostic_Index', 'Blood_Clotting_Score'가 최종 변수로 선택되었습니다. 꽁냥이는 각 스텝별로 모형의 적합 정도를 확인하기 위한 그래프를 그려보았습니다.
fig = plt.figure(figsize=(10,10))
fig.set_facecolor('white')
font_size = 15
plt.xticks(steps,[f'step {s}\n'+'\n'.join(sv_per_step[i]) for i,s in enumerate(steps)], fontsize=12)
plt.plot(steps,adjusted_r_squared, marker='o')
plt.ylabel('Adjusted R Squared',fontsize=font_size)
plt.grid(True)
plt.show()

전진 선택법은 구현 과정이 간단하고 변수가 많은 상황에서도 사용할 수 있다는 장점이 있지만, 한번 선택된 변수는 계속 모형에 존재하며, 일치성(샘플수가 많아질수록 실제 모형에 수렴하는 성질)이 만족되지 않는다는 단점이 있습니다.
3. 후진 소거법(Backward Elimination)
후진 소거법은 전진 선택법과는 반대로 모든 변수가 포함된 모형에서 설명력이 가정 적은 변수를 제거해나가는 방법입니다.
후진 소거법의 과정은 다음과 같습니다.
1 단계) 현재 모형에 포함된 변수를 이용하여 선형 모형을 적합합니다.
2 단계) 추정된 (절편항을 제외한) 회귀 계수에 대하여 가장 큰 $p$-value를 값을 구합니다.
3 단계) 만약 $p$-value에 최대값이 사전에 정의한 유의수준 $\alpha$ 보다 크다면 최대 $p$-value에 대응하는 변수를 기존 모형에서 제외합니다. 그렇지 않다면 후진 소거법 알고리즘을 종료합니다.
$p$-value를 구하는 방법은 앞서 살펴본 전진 선택법에서 구하는 방법과 같습니다. 다음의 코드는 후진 소거법을 구현한 코드입니다.
## 후진 소거법
variables = df.columns[:-2].tolist() ## 설명 변수 리스트
y = df['Survival_Time'] ## 반응 변수
selected_variables = variables ## 초기에는 모든 변수가 선택된 상태
sl_remove = 0.05
sv_per_step = [] ## 각 스텝별로 선택된 변수들
adjusted_r_squared = [] ## 각 스텝별 수정된 결정계수
steps = [] ## 스텝
step = 0
while len(selected_variables) > 0:
X = sm.add_constant(df[selected_variables])
p_vals = sm.OLS(y,X).fit().pvalues[1:] ## 절편항의 p-value는 뺀다
max_pval = p_vals.max() ## 최대 p-value
if max_pval >= sl_remove: ## 최대 p-value값이 기준값보다 크거나 같으면 제외
remove_variable = p_vals.idxmax()
selected_variables.remove(remove_variable)
step += 1
steps.append(step)
adj_r_squared = sm.OLS(y,sm.add_constant(df[selected_variables])).fit().rsquared_adj
adjusted_r_squared.append(adj_r_squared)
sv_per_step.append(selected_variables.copy())
else:
break

후진 소거법을 이용하여 최종 선택된 변수는 'Blood_Clotting_Score', 'Prognostic_Index', 'Enzyme_Test', 'Alc_Heavy'입니다. 전진 선택법에서는 'Liver_Test'가 포함되었지만 여기서는 포함되지 않았습니다. 즉, 후진 소거법과 전진 선택법을 이용한 결과는 다를 수 있습니다. 다음으로 단계별로 수정된 결정계수가 어떻게 변하는지 확인해보겠습니다.
fig = plt.figure(figsize=(10,10))
fig.set_facecolor('white')
font_size = 15
plt.xticks(steps,[f'step {s}\n'+'\n'.join(sv_per_step[i]) for i,s in enumerate(steps)], fontsize=12)
plt.plot(steps,adjusted_r_squared, marker='o')
plt.ylabel('Adjusted R Squared',fontsize=font_size)
plt.grid(True)
plt.show()

변수의 개수가 줄어들어도 수정 결정계수는 증가할 수 있습니다.
후진 소거법 또한 전진 선택법과 마찬가지로 구현 과정이 간단하고 변수가 많은 데이터에 적용 가능하다는 장점이 있습니다. 하지만 한번 제외된 변수는 다시는 모형에 포함될 수 없으며, 일치성을 만족하지 않는 단점이 있습니다.
4. 단계별 선택법(Forward Stepwise Selection)
단계별 선택법은 전진 선택법에서 후진 소거법을 추가한 방법입니다. 단계별 선택법의 과정은 다음과 같습니다.
1 단계) ~ 2 단계)는 전진 선택법과 동일합니다.
3 단계) 최소 $p$-value 값과 미리 정해둔 유의수준 $\alpha$와 비교합니다. 만약 최소 $p$-value < $\alpha$이면 최소 $p$-value에 해당하는 변수를 $S$에 포함시키고 4단계로 넘어갑니다. 그렇지 않은 경우에는 알고리즘을 종료합니다.
4 단계) 추가된 변수를 포함하여 현재 $S$에 있는 모든 변수를 이용하여 선형 모형을 적합합니다. 그리고 추정된 회귀 변수(절편항 제외)에 대하여 가장 큰 $p$-value 값을 구합니다.
5 단계) 최대 $p$-value 값이 사전에 정의된 유의 수준보다 크거나 같으면 해당 변수를 제외하고 1단계로 넘어갑니다. 그렇지 않은 경우에는 제외하는 변수 없이 바로 1단계로 넘어갑니다.
아래 코드는 단계별 선택법을 구현한 코드입니다.
## 전진 단계별 선택법
variables = df.columns[:-2].tolist() ## 설명 변수 리스트
y = df['Survival_Time'] ## 반응 변수
selected_variables = [] ## 선택된 변수들
sl_enter = 0.05
sl_remove = 0.05
sv_per_step = [] ## 각 스텝별로 선택된 변수들
adjusted_r_squared = [] ## 각 스텝별 수정된 결정계수
steps = [] ## 스텝
step = 0
while len(variables) > 0:
remainder = list(set(variables) - set(selected_variables))
pval = pd.Series(index=remainder) ## 변수의 p-value
## 기존에 포함된 변수와 새로운 변수 하나씩 돌아가면서
## 선형 모형을 적합한다.
for col in remainder:
X = df[selected_variables+[col]]
X = sm.add_constant(X)
model = sm.OLS(y,X).fit()
pval[col] = model.pvalues[col]
min_pval = pval.min()
if min_pval < sl_enter: ## 최소 p-value 값이 기준 값보다 작으면 포함
selected_variables.append(pval.idxmin())
## 선택된 변수들에대해서
## 어떤 변수를 제거할지 고른다.
while len(selected_variables) > 0:
selected_X = df[selected_variables]
selected_X = sm.add_constant(selected_X)
selected_pval = sm.OLS(y,selected_X).fit().pvalues[1:] ## 절편항의 p-value는 뺀다
max_pval = selected_pval.max()
if max_pval >= sl_remove: ## 최대 p-value값이 기준값보다 크거나 같으면 제외
remove_variable = selected_pval.idxmax()
selected_variables.remove(remove_variable)
else:
break
step += 1
steps.append(step)
adj_r_squared = sm.OLS(y,sm.add_constant(df[selected_variables])).fit().rsquared_adj
adjusted_r_squared.append(adj_r_squared)
sv_per_step.append(selected_variables.copy())
else:
break

단계별 선택법에서 최종 변수는 'Alc_Heavy', 'Enzyme_Test', 'Prognostic_Index', 'Blood_Clotting_Score'입니다. 후진 소거법에서의 결과와 똑같네요. 단계별 모형 적합 정도를 확인해보겠습니다.
fig = plt.figure(figsize=(10,10))
fig.set_facecolor('white')
font_size = 15
plt.xticks(steps,[f'step {s}\n'+'\n'.join(sv_per_step[i]) for i,s in enumerate(steps)], fontsize=12)
plt.plot(steps,adjusted_r_squared, marker='o')
plt.ylabel('Adjusted R Squared',fontsize=font_size)
plt.grid(True)
plt.show()
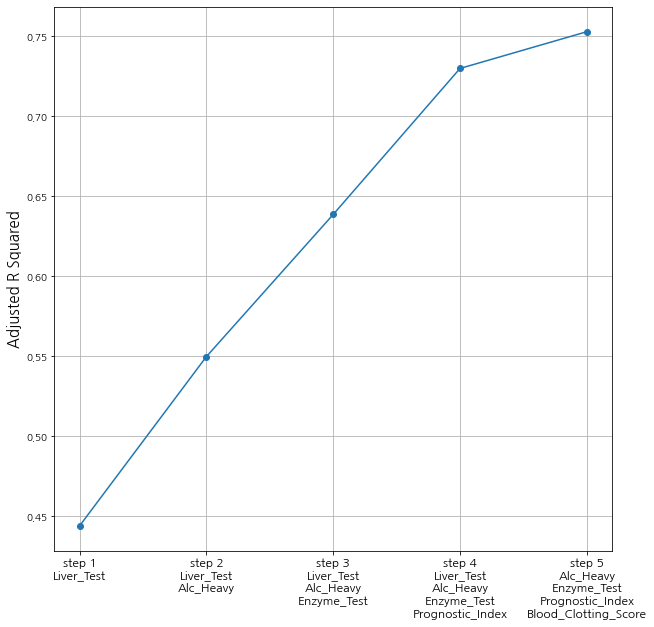
적합 정도가 점점 좋아지는 것을 알 수 있습니다.
단계별 선택법은 구현 과정이 간단하고 한번 들어간 변수는 계속 포함된다는 전진 선택법의 단점을 일부 보완했다는 장점이 있습니다. 하지만 변수가 많아지면 계산량이 늘어난다는 것, 일치성을 만족하지 않는다는 단점이 있지요. 만약 변수 선택법을 수행해야 한다면 전진 선택법, 후진 소거법 보다는 단계별 선택법을 사용하시길 추천드립니다.
지금까지 변수 선택법에 대해서 알아보았습니다. 변수를 선택하는 것은 객관적인 이론은 없고 단순히 경험과 분석자의 판단에 많이 의존하는 경우가 많습니다. 예를 들면 전진 선택법에서의 유의수준은 단순히 분석자의 주관에 따라 결정하는 것처럼 말이죠. 판단이 잘 서지 않는 경우에는 변수 선택법에만 의존하기보다는 관련 분야의 전문가와 상의를 하는 등 다양한 지식을 활용하여 변수를 선택하는 것이 바람직할 거예요.
지금까지 꽁냥이의 글 읽어주셔서 감사합니다~ 안녕히 계세요!!
이번 포스팅에서는 아래의 자료를 참고하였습니다.
Feature selection using Wrapper methods in Python :
Feature selection using Wrapper methods in Python
In today’s era of Big data and IoT, we are easily loaded with rich datasets having extremely high dimensions. In order to perform any…
towardsdatascience.com
'데이터 분석 > 데이터 분석' 카테고리의 다른 글
| [회귀 분석] 8. 이상치(Outlier), 영향점(Influential Point) 탐지 with Python (0) | 2020.11.02 |
|---|---|
| [회귀 분석] 7. 다중공선성 확인하기 - 분산 팽창 인자 with Python (10) | 2020.10.05 |
| [회귀 분석] 5. 최적 모형 선택(All possible search 또는 Best subsets algorithm) with Python (7) | 2020.09.26 |
| [회귀 분석] 4. 오차의 등분산성 검정(테스트)하기 with Python (4) | 2020.09.22 |
| [회귀 분석] 3. 정규분포에 대한 가정 검정하기 with Python (2) | 2020.09.19 |





댓글