안녕하세요~ 꽁냥이에요!
회귀 분석은 관심이 대상이 되는 변수와 설명 변수들 간의 연관성을 파악하기 위한 분석으로써 많이 활용되고 있어요.
이번 포스팅에서는 Python을 이용하여 단순 선형 회귀 모형을 적합하는 방법에 대해서 소개합니다. 회귀 분석에 대한 개념은 아래 포스팅에 정리했어요~.
16. 선형 회귀(Linear Regression) 모형에 대해서 알아보자 with Python
16. 선형 회귀(Linear Regression) 모형에 대해서 알아보자 with Python
머신러닝 관련 포스팅을 하면서 아주 기본적이지만 이론적으로 강력한 선형 회귀 관련 내용을 포스팅하지 않았다는 것에 매우 놀랐다. 이번 포스팅에서는 선형 회귀 모형에 대해서 알아보고 파
zephyrus1111.tistory.com
단순 선형 회귀 모형은 scikit-learn(sklearn) 라이브러리와 statsmodels 라이브러리를 2가지를 이용하여 적합할 수 있어요. 하나씩 살펴볼게요.
2. statsmodels 라이브러리를 이용하여 적합해보기
3. scikit-learn(sklearn)을 이용하여 적합하기
1. 데이터 살펴보기
이번 포스팅에서 다룰 데이터는 회귀분석 예제로 많이 쓰이는 Toluca Company dataset입니다. 데이터를 첨부할 테니 필요하신 분은 다운받아주세요.
변수는 다음과 같습니다.
Lot_size : 제품 크기
Work_hours : 작업 시간
데이터를 살펴볼게요~
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['axes.unicode_minus'] = False ## 마이나스 '-' 표시 제대로 출력
from statsmodels.formula.api import ols
from sklearn.linear_model import LinearRegression
df = pd.read_csv('./toluca_company_dataset.csv') ## 데이터 불러오기line 1~7
이번 포스팅에서 필요한 모듈을 임포트 합니다.
line 9
Pandas에서 제공하는 read_csv 함수를 이용해서 데이터를 불러옵니다.

이번에는 데이터의 분포를 살펴볼게요.
## 시각화
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
font_size = 15
plt.scatter(df['Lot_size'],df['Work_hours']) ## 원 데이터 산포도
plt.xlabel('Lot Size', fontsize=font_size)
plt.ylabel('Work Hours',fontsize=font_size)
plt.show()
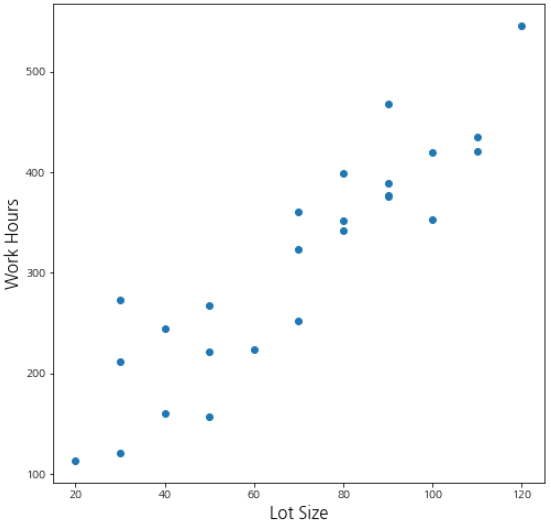
데이터의 분포는 제품 크기가 증가할수록 작업 시간도 증가하는 우상향 패턴을 보이고 있어요.
2. statsmodels 라이브러리를 이용하여 적합해보기
데이터를 보았으니 이제 회귀 모형을 적합시켜 볼게요. 꽁냥이는 작업 시간을 반응 변수로 제품 크기를 설명 변수로 하여 회귀 모형을 적합할 거예요.
statsmodel의 api가 제공하는 ols의 fit 메서드를 통하여 쉽게 적합할 수 있어요. 기본적인 사용법은 다음과 같아요.
ols( ' 반응 변수 ~ 설명 변수 1 + 설명 변수 2 + . . . ', data=데이터).fit( )
아래 코드를 보면 쉽게 이해할 수 있어요.
## states model 사용
fit = ols('Work_hours ~ Lot_size',data=df).fit() ## 단순선형회귀모형 적합
이제 적합 결과를 확인해볼게요. statsmodels 라이브러리는 summary 함수를 제공하는데 이는 적합 결과를 요약해서 보여주는 아주 강력한 기능을 제공합니다.
fit.summary()

위 그림을 보시면 결정계수(R-squared)와 수정 결정계수(Adj. R-squared) 등을 제공하고 회귀계수 추정값, 검정 통계량과 p-value도 제공합니다.
ols는 기본적으로 절편항을 추정합니다. 만약 절편항을 제외하고 싶다면 아래와 같이 모델 표현 문자열에 '-1'을 추가해주세요.
## states model 사용
fit = ols('Work_hours ~ Lot_size - 1',data=df).fit() ## 단순선형회귀모형 적합
회귀 계수 값 자체는 summary 함수를 통해서 볼 수 있지만 직접가져와서 계산을 해야할 때도 있을거예요. 이때 절편이랑 기울기 추정값은 어떻게 얻을 수 있을까요?
## 회귀 계수
print(fit.params.Intercept) ## 절편
print(fit.params.Lot_size) ## 기울기
절편항은 Intercept를 통하여 기울기는 해당 변수 이름으로 접근하여 얻을 수 있습니다.

절편은 약 62.37, 기울기는 약 3.57으로 추정되었습니다.
그리고 학습에 사용된 설명변수에 대응하는 작업시간의 추정치는 다음과 같이 fittedvalues 필드를 통하여 얻을 수 있습니다.
## 추정값
fit.fittedvalues
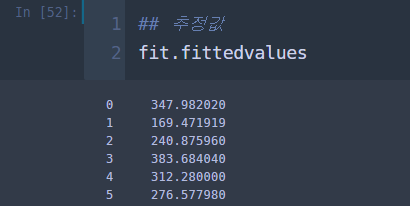
또한 모델 검증에 필요한 잔차는 resid 필드를 이용하여 구할 수 있습니다.
## 잔차
fit.resid

그리고 새로운 데이터 즉, 새로운 제품 크기에 대한 작업 시간의 예측값을 얻고 싶다면 다음과 같이 해주세요.
## 예측값
fit.predict(exog=dict(Lot_size=[80]))
위 코드와 같이 predict 함수의 exog인자에 설명 변수 이름과 해당 값을 딕셔너리로 넘겨주셔야 합니다.

제품 크기가 80이라면 작업 시간은 약 348시간이 걸린다고 예측할 수 있어요.
이제 회귀 직선을 그려볼까요? 아래 코드를 실행해주세요.
## 시각화
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
font_size = 15
plt.scatter(df['Lot_size'],df['Work_hours']) ## 원 데이터 산포도
plt.plot(df['Lot_size'],fit.fittedvalues,color='red') ## 회귀직선 추가
plt.xlabel('Lot Size', fontsize=font_size)
plt.ylabel('Work Hours',fontsize=font_size)
plt.show()
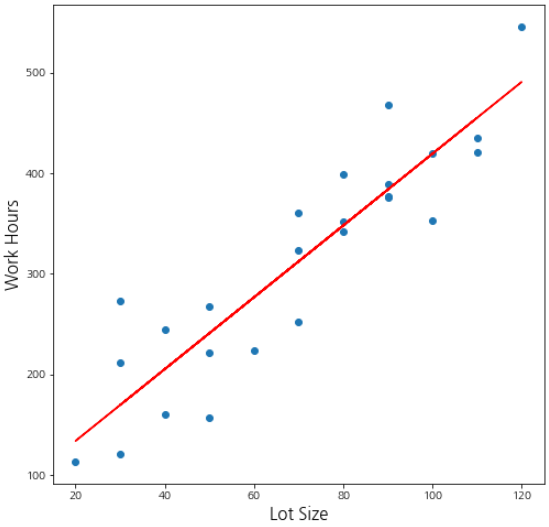
이번에는 제품 크기에 대한 잔차도를 그려보겠습니다. 잔차도는 모형이 잘 적합되었는지를 시각적으로 확인하기 위해 필요한 그래프예요.
## 잔차도 Residual Plot
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
font_size = 15
plt.scatter(df['Lot_size'],fit.resid) ## 잔차도 출력
plt.xlabel('Lot Size', fontsize=font_size)
plt.ylabel('Residual', fontsize=font_size)
plt.show()

잔차도를 보니 특별히 잔차에 패턴은 보이지 않네요.
3. scikit-learn(sklearn)을 이용하여 적합하기
이번에는 scikit-learn(sklearn)을 이용하여 단순 선형 회귀 모형을 적합해보도록 하겠습니다. 적합은 LinearRegression 클래스의 fit 메서드를 이용합니다. 기본적인 사용법은 다음과 같아요.
LinearRegression( ).fit(설명 변수 2차원 어레이, 반응 변수)
## sklearn linear regression 사용
x = df['Lot_size'].values.reshape(-1,1) ## 차원 증가 시켜준다.
y = df['Work_hours']
fit = LinearRegression().fit(x,y) ## 단순선형회귀모형 적합line 2
statsmodels과 달리 설명변수의 차원을 하나 증가시켜주어야 해요.
line 5
LinearRegression 클래스의 fit 메서드를 이용하여 모형을 적합합니다.
회귀 계수 추정값을 살펴볼까요?
## 회귀 계수
print(fit.intercept_) ## 절편
print(fit.coef_) ## 기울기

절편은 약 62.37, 기울기는 약 3.57으로 추정되었습니다. 이는 앞서 본 것과 동일합니다.
statsmodels에서는 fittedvalues를 통하여 학습 데이터의 설명 변수에 대응하는 작업 시간의 추정값을 일괄적으로 구할 수 있었지만 sklearn에서는 다음과 같이 predict 함수를 사용합니다.
## 추정값
fit.predict(x)

앞서 본 것과 동일한 추정값을 얻을 수 있습니다.
sklearn에서는 잔차를 따로 제공하지 않아서 직접 계산을 해주어야 합니다.
## 잔차
residual = y - fit.predict(x)
print(residual)

잔차 또한 앞서 본 것과 동일합니다.
이번에는 예측값을 계산해보겠습니다. predict함수에 이중 각괄호를 이용하여 값을 넘겨주면 됩니다.
## 예측값
fit.predict([[80]])

제품 크기가 80이라면 작업 시간은 약 348시간이 걸린다고 예측할 수 있어요. 이는 앞서 본 것과 동일한 결과입니다.
꽁냥이는 회귀 모형을 적합할 때 scikit-learn보다는 statsmodel을 이용할 것을 강력히 추천합니다.
왜냐하면 statsmodels는 1) summary 함수를 통해 요약정보를 확인할 수 있고요. 2) 잔차와 학습 데이터에 대한 반응 변수의 추정 값을 따로 계산하지 않아도 되고요. 여기서는 다루지 않았지만 범주형 데이터의 경우 scikit-learn은 데이터를 전처리해주어야 하는 불편함이 있는 반면 statsmodels의 경우 3) 전처리가 필요 없이 범주형 데이터를 바로 모형에 적합할 수 있어요.
이번 포스팅에서는 단순 선형 회귀 모형을 적합하는 방법에 대해서 알아보았어요. 지금까지 꽁냥이의 글 읽어주셔서 감사합니다. 더 좋은 내용으로 찾아뵐게요. 안녕히 계세요~!!
'데이터 분석 > 데이터 분석' 카테고리의 다른 글
| [회귀 분석] 3. 정규분포에 대한 가정 검정하기 with Python (2) | 2020.09.19 |
|---|---|
| [회귀 분석] 2. 잔차도(Residual plot)와 QQ plot 그리기 (0) | 2020.09.18 |
| [A/B 테스트] 2. A/B 테스트 사례에 대하여 알아볼까요?! (0) | 2020.08.09 |
| [A/B 테스트] 1. A/B 테스트란 무엇일까요? (0) | 2020.07.24 |
| [RFM 고객 분석] 3. Python을 이용한 RFM 분석 - RFM 가중치 계산 (420) | 2020.06.28 |





댓글