이번 포스팅에서는 클러스터링 알고리즘 중 하나인 DBSCAN(Density-Based Spatial Clustering of Applications with Noise)에 대해서 알아보고자 한다.
- 목차 -
1. DBSCAN이란 무엇인가?
1) 정의
DBSCAN은 Density-Based Spatial Clustering of Applications with Noise의 준말로 그 정의는 다음과 같다.
DBSCAN은 서로 인접한 데이터들은 같은 클러스터일 것이라는 아이디어에 착안하여 만들어졌으며 특정 데이터를 중심으로 밀도가 높은 곳에 포함된 데이터에는 클러스터를 할당하고 밀도가 낮으면 그 데이터를 노이즈로 취급하는 알고리즘이다.
2) 파헤치기
위의 정의를 하나하나 살펴보자.
a. DBSCAN은 서로 인접한 데이터들은 같은 클러스터 내에 있다는 것을 가정한 알고리즘이다.
이 말이 어찌 보면 당연한 것 같아서 기존 클러스터링 알고리즘(예 : K-means)과 무엇이 다르냐고 할 수 있다. DBSCAN과 K-Means의 차이점은 DBSCAN은 서로 인접한 데이터들을 같은 클러스터에 할당하는 것이고 K-Means는 클러스터 중심치와 가까운 데이터를 해당 클러스터로 할당한다는 차이가 있다. 아래 그림을 살펴보자.
다음과 같은 데이터가 있다고 할 때 두개의 클러스터를 각 데이터에 할당한다고 생각해보자.

K-means 알고리즘은 중심과 데이터의 거리 기반에 따른 클러스터링 알고리즘이다. 이에 따라 아래 그림에서 빨간 점이 두 클러스터의 중심으로 주어진 경우 각 데이터들은 중심과 가까운 쪽의 클러스터로 할당될 것이다. 2차원의 경우 두 중심을 이은 선분의 수직 이등분선이 클러스터를 나누는 경계가 된다.

하지만 K-Means 클러스터링 알고리즘의 결과는 뭔가 어색하다.
위 클러스터링 결과에서 문제가 되는 부분은 아래 그림에서 회색 점인데 왼쪽은 그 회색점을 초록색으로 클러스터링 한 경우이고 오른쪽은 보라색으로 클러스터링 한 경우이다(K-Means 알고리즘의 결과와 동일).

왼쪽 그림의 경우 회색점이 초록색 점들과 촘촘하게 이어진(밀도가 높은) 클러스터이며 굉장히 자연스럽다. 하지만 오른쪽의 경우 보라색 점들 사이에는 촘촘하게 이어져있지만 회색 점들을 포함시키면 중간에 빈 공간(밀도가 낮은 공간)이 생겨 어색하다.
K-Means 알고리즘이 어색한 클러스터링 결과를 보여주는 이유는 앞에서 살펴보았듯이 데이터들끼리 촘촘하게 이어지는 정도 즉, 밀도(Density)를 제대로 반영하지 못하기 때문이다. K-Means는 밀도가 높으나 낮으나 중심치와의 거리만 가까우면 같은 클러스터라고 생각하기 때문에 어색한 클러스터링 결과를 보여준 것이다.
DBSCAN은 이러한 K-Means 알고리즘의 약점을 극복한 것으로 서로 촘촘하게 연결된 달리 표현하면 가깝게 인접해있는 데이터들은 같은 클러스터라 가정하고 인접한 데이터를 잘 찾아서 클러스터를 할당하는 알고리즘인 것이다.
b. DBSCAN은 특정 데이터를 중심으로 밀도가 높은 곳에 포함된 데이터에는 클러스터를 할당하고 밀도가 낮으면 그 데이터를 노이즈로 취급하는 알고리즘이다.
DBSCAN은 인접한 데이터끼리는 같은 클러스터라고 가정한다고 했다. 그렇다면 이제 인접한 데이터인지 아닌지 어떻게 판단하고 클러스터를 어떻게 할당하는지 알아보자.
1 단계) 핵심 데이터와 비 핵심 데이터 나누기
DBSCAN은 데이터를 2가지 타입으로 분류하는데 하나는 핵심 데이터(Core Point)와 비 핵심 데이터(Non-Core Point)로 나눈다. 핵심 데이터와 비 핵심 데이터로 나누는 기준은 밀도가 높은 데이터 집합에 속해있는지를 여부로 판단한다(이러한 의미에서 DBSCAN은 Density-Based Spatial 클러스터링 알고리즘이다). 이때 밀도가 높은 데이터 집합에 속한다면 핵심 데이터 아니면 비 핵심 데이터로 나뉜다.
그렇다면
밀도가 높은 데이터 집합의 포함되는지 여부는 어떻게 판단할까?
DBSCAN은 2가지 파라미터를 사전에 설정하는데 반경(epsilon)과 반경 안에 있어야할 최소 샘플수이다. 반경, 최소 샘플수와 밀도와의 관계를 살펴보자.
당연하게도 한 데이터가 밀도가 높은 데이터 집합에 속한다면 그 데이터를 중심으로 (작은) 사전에 정해둔 반경 내에 데이터가 포함되어 있어야 할 것이다.

그렇다면 위의 빨간 점은 핵심 데이터인가? 반경만 가지고는 충분하지 않다. 왜냐하면 아래의 경우를 살펴보자. 아래 그림은 빨간 점을 중심으로 특정 반경 내에 데이터를 포함하고 있지만 빨간 경계 속 밀도가 높은 데이터에 비해서는 그 데이터가 충분하지 않다.
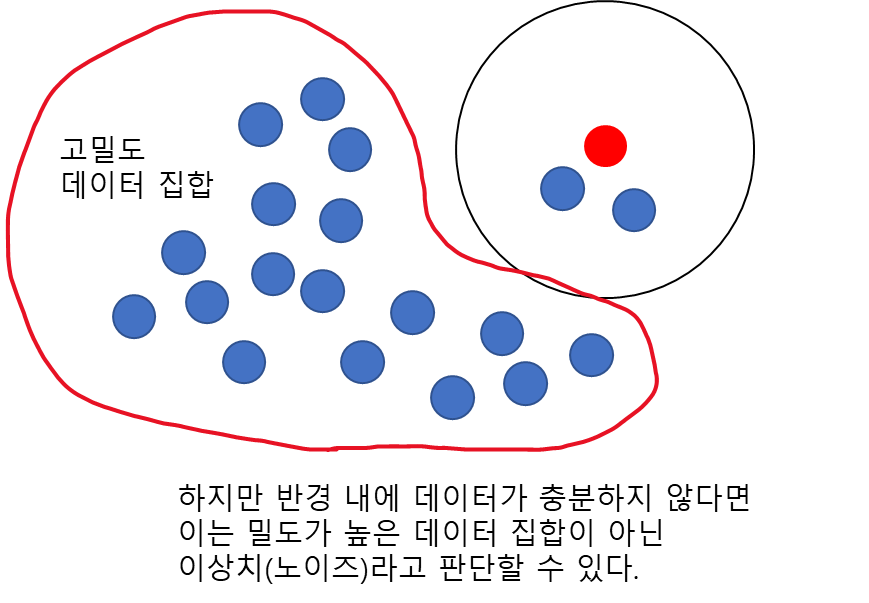
이런 경우는 대세에서 벗어나 돌발 행동하는 데이터, 즉 노이즈로 생각할 수 있다. 이러한 노이즈는 일반적으로 그 주변에 샘플 수가 적다. 따라서 반경 뿐만 아니라 그 반경 내에 들어오는 최소 샘플 수를 같이 고려해야 한다. 이때 위의 빨간 점은 비핵심 데이터가 된다.
반경 내 최소 샘플 수를 5개로 설정하면 아래의 빨간 점은 최소 샘플 수 이상을 반경 내에 포함하고 있으므로 핵심 데이터가 된다.
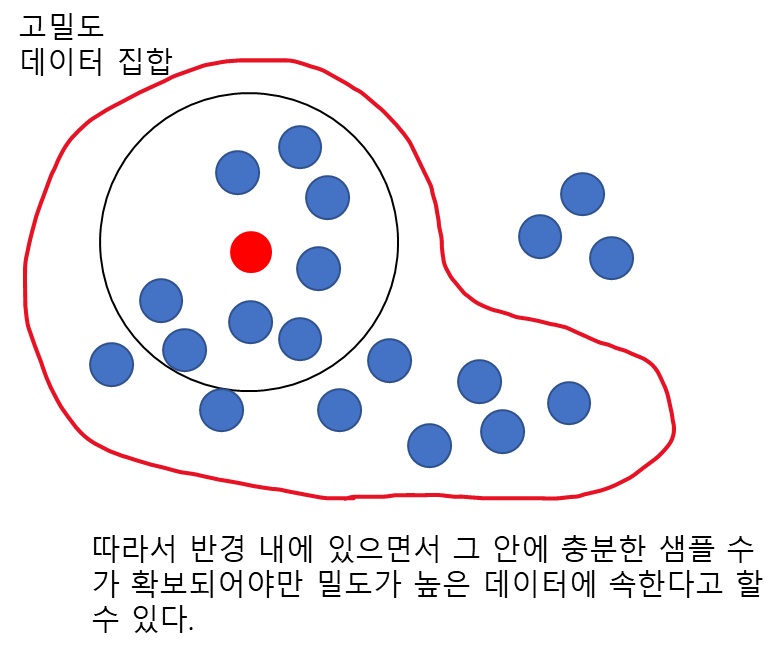
종합하면 특정 데이터가 밀도가 높은 데이터인지 아닌지는 그 데이터 반경 안에 데이터가 충분히 포함되어야 밀도가 높다고 판단하는 것이다. 이때 충분하다는 것은 반경 내 최소 샘플 수 이상인 것으로 판단한다.
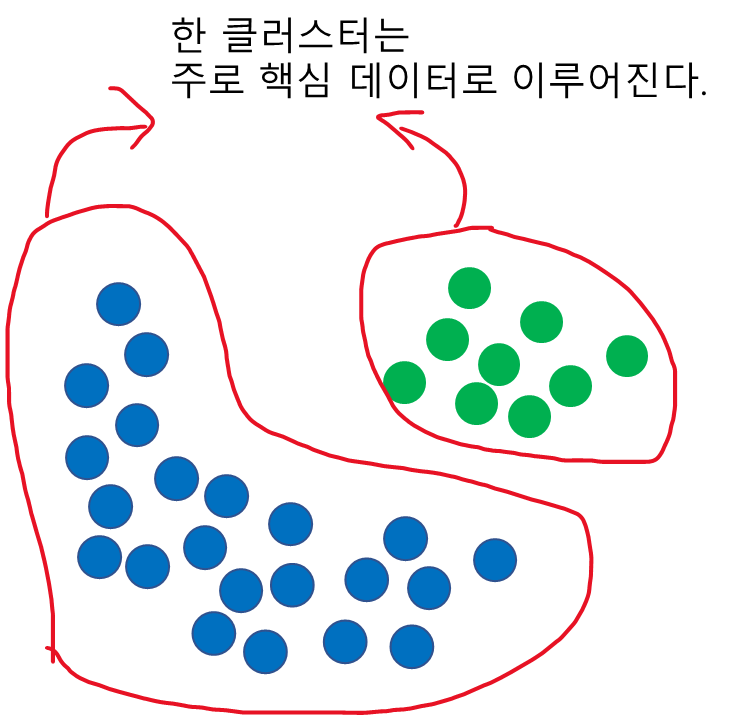
DBSCAN 알고리즘이 데이터를 핵심, 비 핵심 데이터로 나누는 이유는 클러스터를 구성하는 주요 데이터는 핵심 데이터라고 판단하기 때문이다.
2 단계) 핵심 데이터 클러스터링 할당하기
이제 DBSCAN 알고리즘이 클러스터를 할당하는 방법을 알아보자. 먼저 아래와 같은 데이터가 있다고 해보자.

반경이 다음과 같고 최소 샘플 수는 4라고 설정했다고 해보자. 이를 통해 모든 데이터를 핵심 데이터와 비 핵심 데이터를 나눈다.
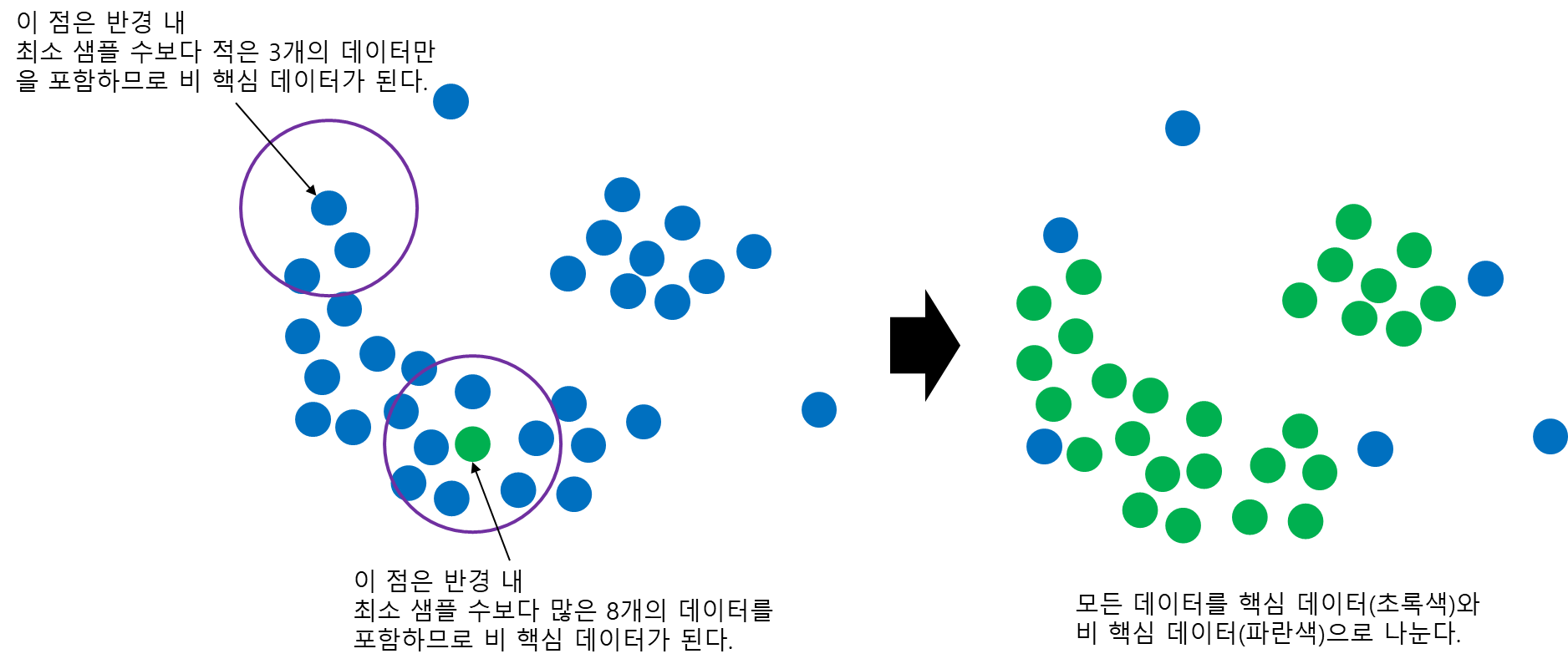
이제 핵심 데이터를 하나 랜덤하게 선택하고 반경 내 핵심 데이터(Core Point)들을 같은 클러스터로 할당한다. 이때 반경 내 비 핵심 데이터(Non-core Point)는 클러스터를 아직 할당하지 않는다. 다음으로 자기 자신을 제외한 나머지 핵심 데이터(Core Point)에 대해서 이전 과정을 반복한다. 이는 더 이상 같은 클러스터를 할당할 수 없을 때까지 반복한다. 이렇게 되면 핵심 데이터에 대한 첫 번째 클러스터 할당이 완료된 것이다.
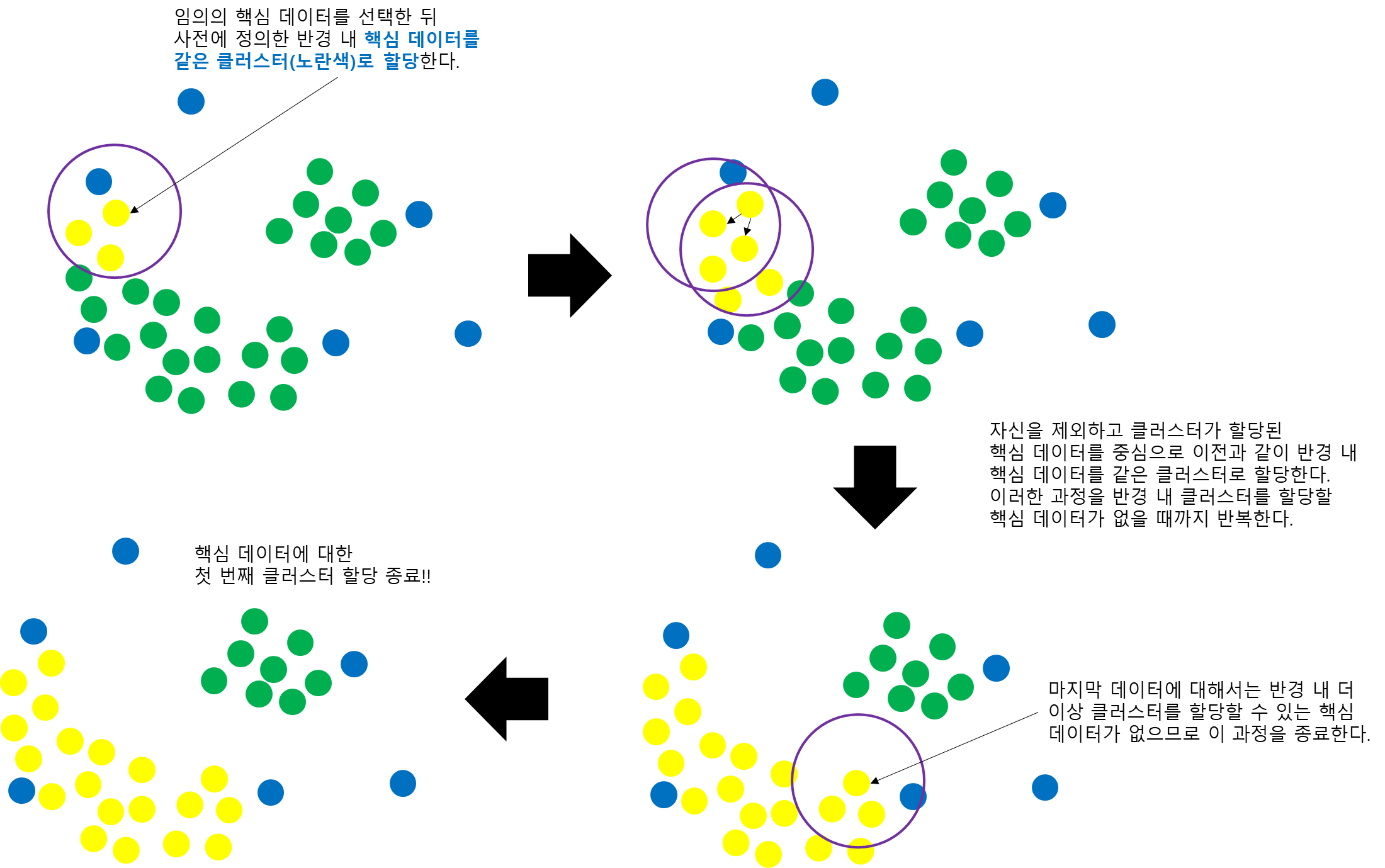
3 단계) 비 핵심 데이터 클러스터링 할당하기
아직 끝나지 않았다. 비 핵심 데이터 중에서 핵심 데이터로 이루어진 클러스터에 가까운 것들은 클러스터에 포함시키는 것이다.
먼저 비 핵심 데이터를 하나 선택하고 반경 내 가장 가까운 핵심 데이터를 찾는다. 이 핵심 데이터에 대응하는 클러스터로 비 핵심 데이터를 포함시킨다.
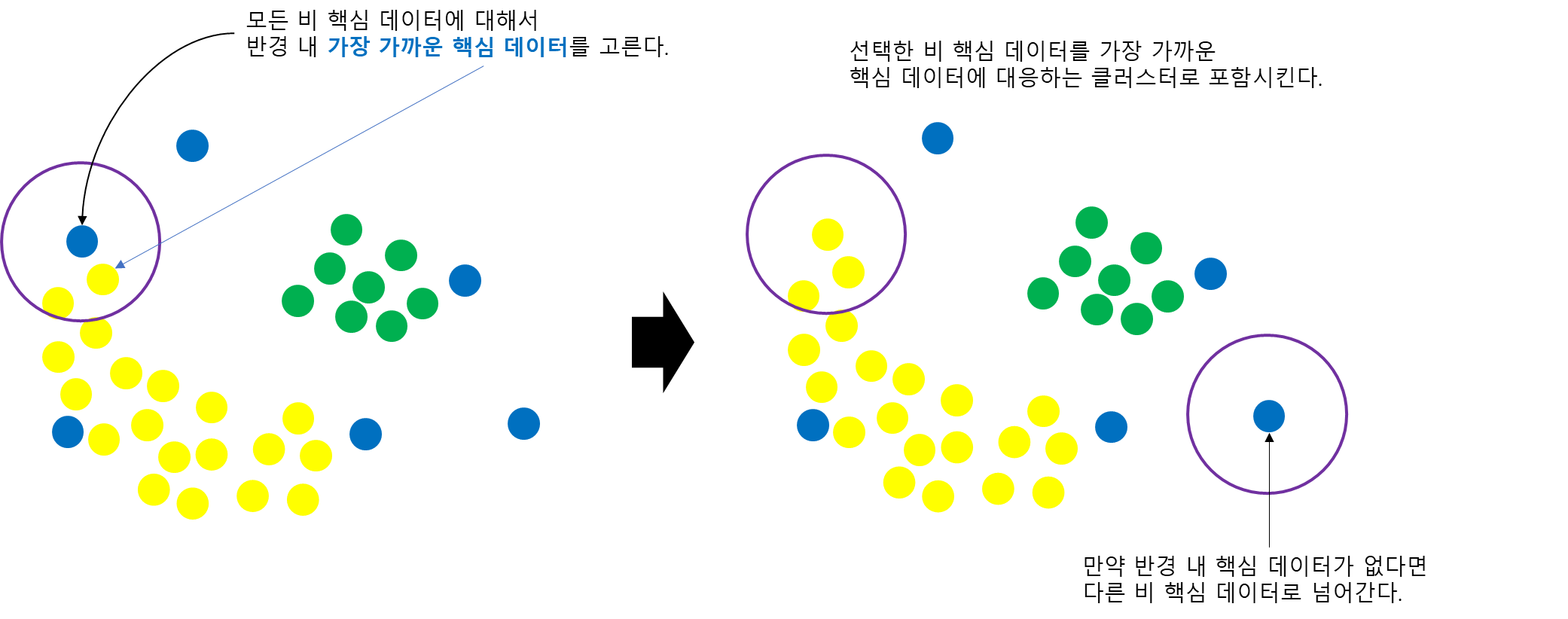
이 과정이 끝나면 첫 번째 클러스터 할당이 완전히 종료된다. 즉, DBSCAN은 핵심 데이터로 이루어진 클러스터와 가까운 비 핵심 데이터도 클러스터에 포함시켜준다.
이제 남은 핵심 데이터에 대해서 2~3 단계 과정을 반복하며 더 이상 할당할 핵심 데이터가 없으면 종료된다.
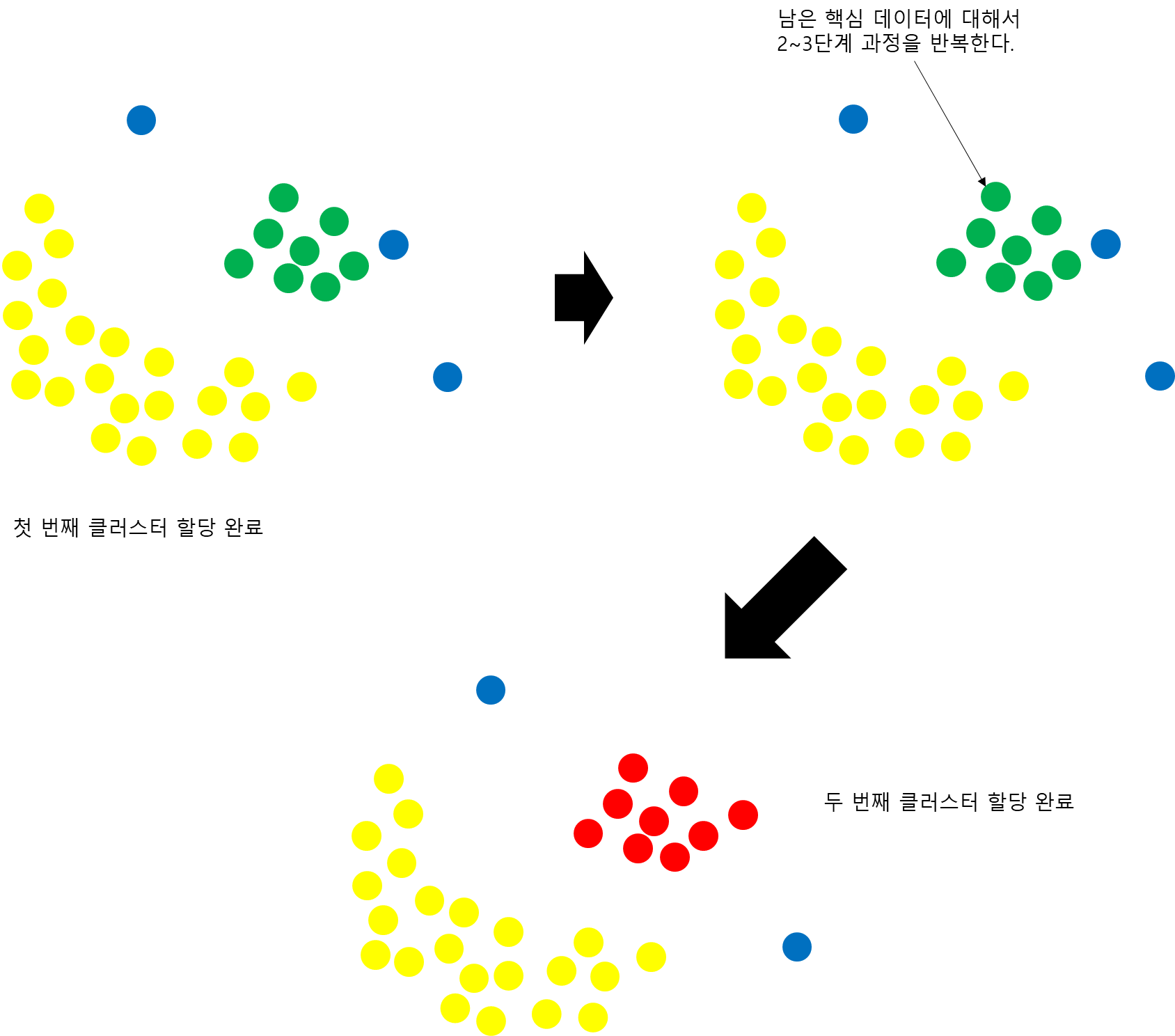
이때 주목할 점이 2가지가 있는데 첫 번째는 DBSCAN은 모든 데이터에 대해서 클러스터를 할당하는 것이 아니라는 것이다. 위 그림에서 2개의 파란 점은 마지막까지 클러스터를 할당받지 못한다. DBSCAN은 이 파란 점들을 비핵심 데이터들 중에서 노이즈라고 판단한 것이다. 정리하면 DBSCAN은 비 핵심 데이터를 두 가지로 판단하는데 하나는 클러스터 내에서 조금 떨어져 있는 데이터, 다른 하나는 노이즈라고 판단한다. 이때 클러스터 내에서 조금 떨어져 있는 비 핵심 데이터는 같은 클러스터라 생각하여 클러스터를 할당하고 노이즈는 그 어떤 클러스터에서도 생성되지 않은 것이라 여겨 클러스터를 할당하지 않는 것이다.
두 번째는 DBSCAN의 결과로 얻어진 클러스터의 개수는 사전에 설정하는 것이 아닌 자동으로 결정된다는 것이다. K-Means나 Gaussian Mixture 클러스터링과 달리 DBSCAN은 사전에 클러스터 개수를 설정하지 않고 알고리즘 수행 과정에서 자동으로 결정된다.
3) 특징
DBSCAN의 특징은 다음과 같다.
첫째, 모든 데이터에 클러스터를 할당하는 것은 아니다.
DBSCAN은 주어진 반경 내에 최소 샘플 수이상 데이터가 없고 반경 내 클러스터가 할당된 데이터가 없다면 노이즈로 판단하여 클러스터를 할당하지 않는다.
둘째, DBSCAN은 반경과 최소 샘플 수를 조절하여 여러 형태의 클러스터 패턴을 잡아낼 수 있다.
DBSCAN 알고리즘으로 만들어진 클러스터링 결과를 반경과 최소 샘플 수의 변화에 따라서 어떻게 변하는지 살펴보자.
먼저 최소 샘플 수를 고정시키고 반경을 변화시킨다고 해보자. 아래 그림과 같이 반경이 작아질수록 듬성 듬성한 클러스터에서 촘촘한 패턴을 갖는 클러스터를 구성하게 된다.
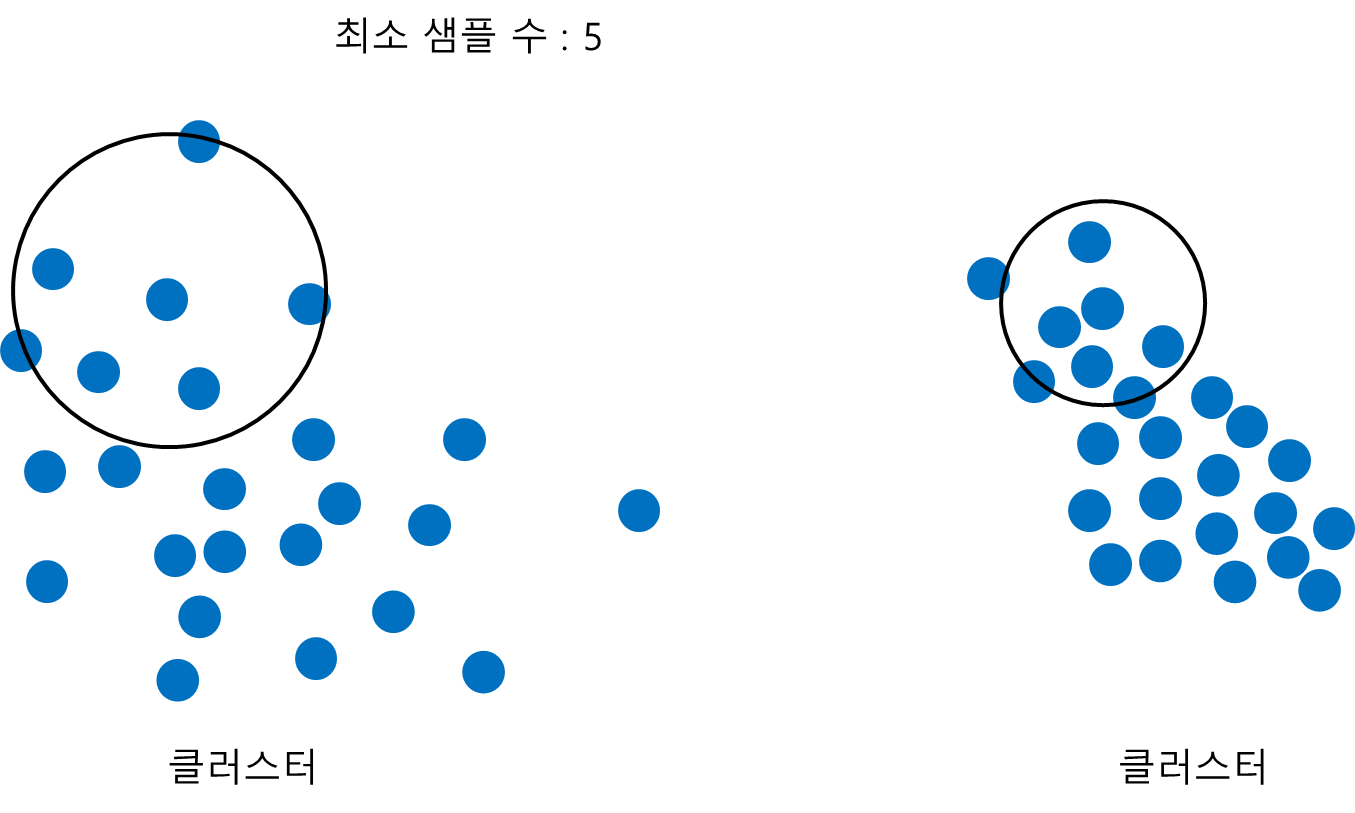
반대로 반경을 고정시키고 최소 샘플 수를 변화시킨다고 해보자. 아래 그림과 같이 반경 내에 들어가야하는 최소 샘플 수가 커질수록 더욱 촘촘한 패턴을 갖는 클러스터를 구성하게 된다.
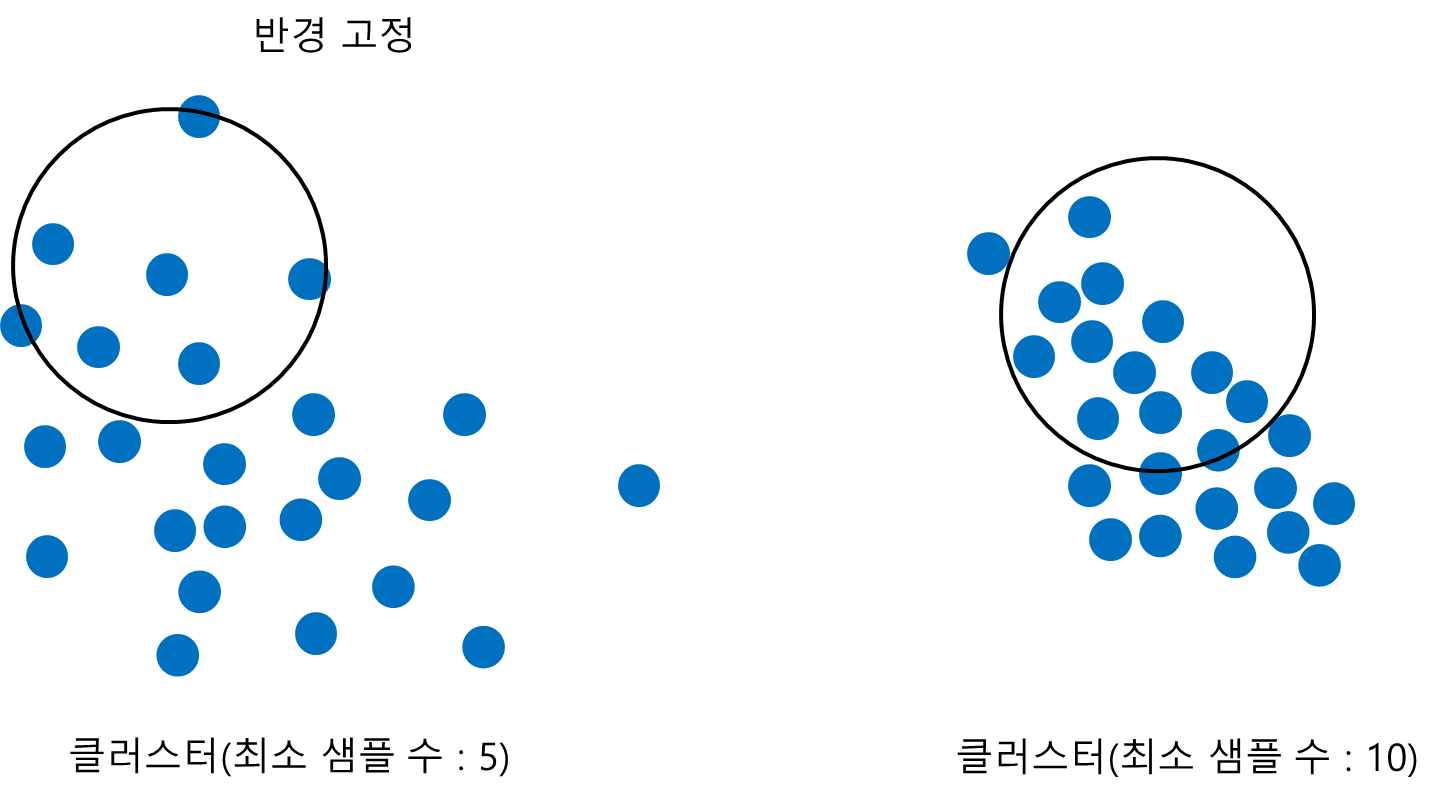
종합하면 반경과 최소 샘플 수를 이용하여 데이터의 밀도가 높거나 낮은 클러스터 패턴을 잡아낼 수 있다.
셋째 DBSCAN의 결과로 얻어진 클러스터의 개수는 자동으로 결정된다는 것이다.
DBSCAN은 더 이상 할당할 핵심 데이터(Core Point)가 없다면 알고리즘을 종료함과 동시에 자연스럽게 클러스터 개수가 결정된다.
2. DBSCAN 알고리즘
DBSCAN 알고리즘을 정리해보자.
DBSCAN Algorithm
주어진 데이터 $S = \{x_1, \ldots, x_n\}, x_i\in \mathbb{R}^p$가 있다고 하자. 반경 $\epsilon >0$과 최소 샘플 수 $N$, 클러스터 라벨 $k=0$으로 설정한다. DBSCAN은 다음의 단계를 반복한다.
1 단계) 모든 데이터 $x_i$를 핵심 데이터(Core Point)와 비 핵심 데이터(Non-Core Point)로 나눈다. 핵심 데이터 집합 $C$은 다음을 만족한다.
$$C = \{ x \in S : \text{#}\{z \in S : d(x, z) < \epsilon \} \geq N \}$$
여기서 $\text{#}A$는 $A$ 집합의 원소 개수이다. 그리고 비 핵심 데이터 집합은 $NC = S-C$ 이다.
2 단계) 핵심 데이터 클러스터 할당
2-1) 핵심 데이터 $x' \in C$를 선택하여 클러스터 $k$를 할당한다.
2-2) 그다음 $x'$를 중심으로 $\epsilon$ 내에 있는 핵심 데이터 또한 클러스터 $k$를 할당한다.
2-3) $x'$를 제외하고 클러스터를 할당받은 핵심 데이터에 대하여 더 이상 클러스터를 할당할 핵심 데이터가 없을 때까지 2-2)를 반복한다.
3 단계) 비 핵심 데이터 클러스터 할당
모든 비 핵심 데이터 $z' \in NC$에 대하여 $z'$을 중심으로 반경 내 핵심 데이터가 있는 경우 클러스터 $k$를 할당한다.
4 단계) 클러스터를 할당받지 못한 핵심 데이터가 있는 경우 클러스터 라벨을 $k=k+1$로 세팅하고 핵심 데이터 하나를 선택하여 2~3 단계)를 반복한다. 클러스터를 할당받지 못한 핵심 데이터가 없는 경우 알고리즘을 종료한다.
3. DBSCAN 장단점
- 장점 -
a. 사전에 클러스터 개수를 설정할 필요가 없다.
b. DBSCAN을 이용하여 이상치를 발견할 수 있다.
DBSCAN은 비 핵심 데이터 중에서도 클러스터와 인접하지 않으면 노이즈라 판단하여 클러스터를 할당하지 않는다. 이러한 노이즈를 이상치로 생각한다면 이상치를 탐지하는데 DBSCAN을 활용할 수 있다.
c. DBSCAN은 클러스터 결과가 이상치에 영향을 받지 않는다.
DBSCAN은 반경 내에 있는 인접한 핵심 데이터를 이동하면서 클러스터를 할당하므로 이상치에 영향을 받지 않게 된다.
d. 웬만한 클러스터 패턴을 잡아낼 수 있다.
e. 구현이 쉽다.
?? 재귀적으로 클러스터를 할당하는 부분과 비 핵심 데이터 중에서 클러스터를 할당하는 부분과 안 하는 부분을 구현하는 게 꽤나 까다로웠다. 사람들은 쉽다고 하는데 난 어려웠다 ㅠ.
- 단점 -
a. 고차원 데이터에 대해서는 잘 작동하지 않는다.
b. 듬성 듬성한 데이터(Sparse Data)에 대해선 클러스터 결과가 썩 좋지 않다.
4. 파이썬(Python) 구현
이제 알고리즘을 알았으니 파이썬으로 구현해보자. 아래 코드는 DBSCAN 알고리즘을 통하여 주어진 데이터에 클러스터를 할당한다.
class myDBSCAN():
def __init__(self, eps=5, min_samples=5):
self.eps = eps
self.min_samples = min_samples
self.is_core = None
self.labels = None
self.X = None
def get_neighbor(self, point, data, eps):
## eps 반경에 들어오는 데이터 여부
return np.linalg.norm(data-point, axis=1)<eps
def get_closest(self, target_idx, others_idx, X, eps):
## 자신을 제외한 가장 가까운 데이터 인덱스 반환
point = X[target_idx]
data = X[others_idx]
return others_idx[np.argmin(np.linalg.norm(data-point, axis=1))]
def fit(self, X):
def assign_cluster(core_idx, X, is_core, eps):
if core_idx in visited_idx:
return
visited_idx.append(core_idx)
neighbor_idx = np.where(self.get_neighbor(X[core_idx], X, eps) == True)[0]
neighbor_idx = set(neighbor_idx)-set(non_core_idx)
if len(neighbor_idx) == 0:
return
for ni in neighbor_idx:
if labels[ni] == -1:
labels[ni] = cluster_label
other_idx = np.array(list(set(neighbor_idx)-set(visited_idx)))
for ci in other_idx:
assign_cluster(ci, X, is_core, eps)
## Assign core and non-core
is_core = []
for i in range(X.shape[0]):
target_data = X[i]
if np.sum(self.get_neighbor(target_data, X, eps)) >= min_samples:
is_core.append(1)
else:
is_core.append(-1)
is_core = np.array(is_core)
self.is_core = is_core
## Assign Cluster
labels = np.array([-1]*X.shape[0])
core_indice = np.where(is_core == 1)[0]
init_core_idx = core_indice[0] ## initial core point
cluster_label = 0
labels = np.array([-1]*X.shape[0])
non_core_idx = np.where(is_core == -1)[0]
visited_idx = [] ## 클러스터 할당된 core point
prev_cluster_list = [] ## 이전 클래스 라벨 리스트
while True:
assign_cluster(init_core_idx, X, is_core, eps) ## Assign core point cluster
temp_labels = labels.copy()
temp_not_assign_cluster_idx = np.where(labels == -1)[0]
assign_cluster_idx = [i for i, x in enumerate(labels) if x != -1 and x in prev_cluster_list]
## Assign non core point cluster
for nci in non_core_idx:
others_idx = np.array(list(set(range(X.shape[0]))-set([nci])))
neighbor_idx = np.where(self.get_neighbor(X[nci], X, eps) == True)[0]
if len(neighbor_idx) == 0:
continue
others_idx = set(neighbor_idx) - set(temp_not_assign_cluster_idx)-set([nci])-set(assign_cluster_idx)
if len(others_idx) == 0:
continue
others_idx = np.array(list(others_idx))
closest_neighbor_idx = self.get_closest(nci, others_idx, X, eps)
labels[nci] = labels[closest_neighbor_idx]
not_assign_cluster_idx = np.where(labels == -1)[0]
if len(set(core_indice).intersection(not_assign_cluster_idx)) == 0:
break
core_indice = np.array(list(set(core_indice).intersection(not_assign_cluster_idx)))
non_core_idx = np.array(list(set(non_core_idx).intersection(not_assign_cluster_idx)))
init_core_idx = core_indice[0] ## initial core point
prev_cluster_list.append(cluster_label)
cluster_label += 1
visited_idx = np.where(labels != -1)[0].tolist()
self.labels = labels
return self
line 1~7
myDBSCAN 클래스는 반경과 최소 샘플 수를 받게 했다.
line 9~17
특정 포인트를 중심으로 반경 내에 데이터가 들어오는지 여부를 반환하는 get_neighbor, 특정 데이터를 중심으로 가장 가까운 다른 데이터의 인덱스를 반환하는 get_closest 메서드를 정의했다.
line 19~83
제일 중요한 fit 메서드이다. 우선 핵심 데이터에 클러스터를 할당하는 함수 assign_cluster를 내부에 정의했다(line 20~33). assign_cluster는 재귀적으로 핵심 데이터에 클러스터를 할당하며 반경 내 클러스터를 할당받지 못한 데이터 또는 반경 내 데이터가 없다면 종료한다.
다음으로 모든 데이터를 핵심 데이터와 비 핵심 데이터로 나눈다(line 35~44). 다음으로 클러스터를 할당한다. 이때 핵심 데이터에 대해서 클러스터를 할당한 뒤(line 56), 비 핵심 데이터를 클러스터로 할당한다(line 61~72). 이제 클러스터를 할당받지 못한 핵심 데이터가 없다면 종료하고 아니면 클러스터 할당 과정을 반복하게 된다.
5. 예제
구현을 했으니 테스트를 해볼 시간이다. 여기에서는 내가 구현한 것과 Scikit-Learn에서 제공하는 DBSCAN 클래스를 사용하여 클러스터링 한 후 그 결과를 비교해보고자 한다.
데이터는 아래의 지출 점수 관련 데이터를 사용했으며 아래에 첨부해 두었다.
여기서는 지출 점수(Spending_Score)와 연 수입(Annual_Income)만 고려했다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
df = pd.read_excel('./dbscan_test.xlsx')
fig = plt.figure()
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(df['Spending_Score'], df['Annual_Income'])
plt.show()
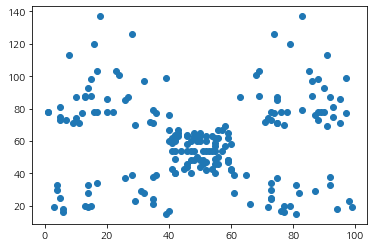
이제 내가 만든 myDBSCAN을 이용하여 클러스터를 할당하고 그 결과를 시각화해보았다.
eps = 10
min_samples = 5
X = df[['Spending_Score','Annual_Income']].values
my_cluster = myDBSCAN(eps=eps, min_samples=min_samples).fit(X)
fig = plt.figure()
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(df['Spending_Score'], df['Annual_Income'], c=my_cluster.labels)
plt.show()
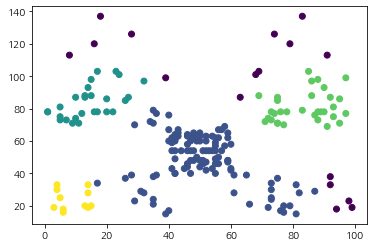
보라색 점들은 노이즈이며 총 4개의 클러스터가 생성된 것을 알 수 있다. 꽤나 합리적인 결과가 나왔다. 이러한 클러스터가 생기기까지의 과정을 순차적으로 살펴보기 위해 시각화해보자. 먼저 핵심 데이터(노라색)와 비 핵심 데이터(보라색)은 아래 그림과 같다.
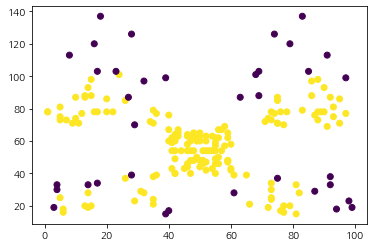
그 다음 4개의 클러스터를 할당하는 과정은 다음과 같다.
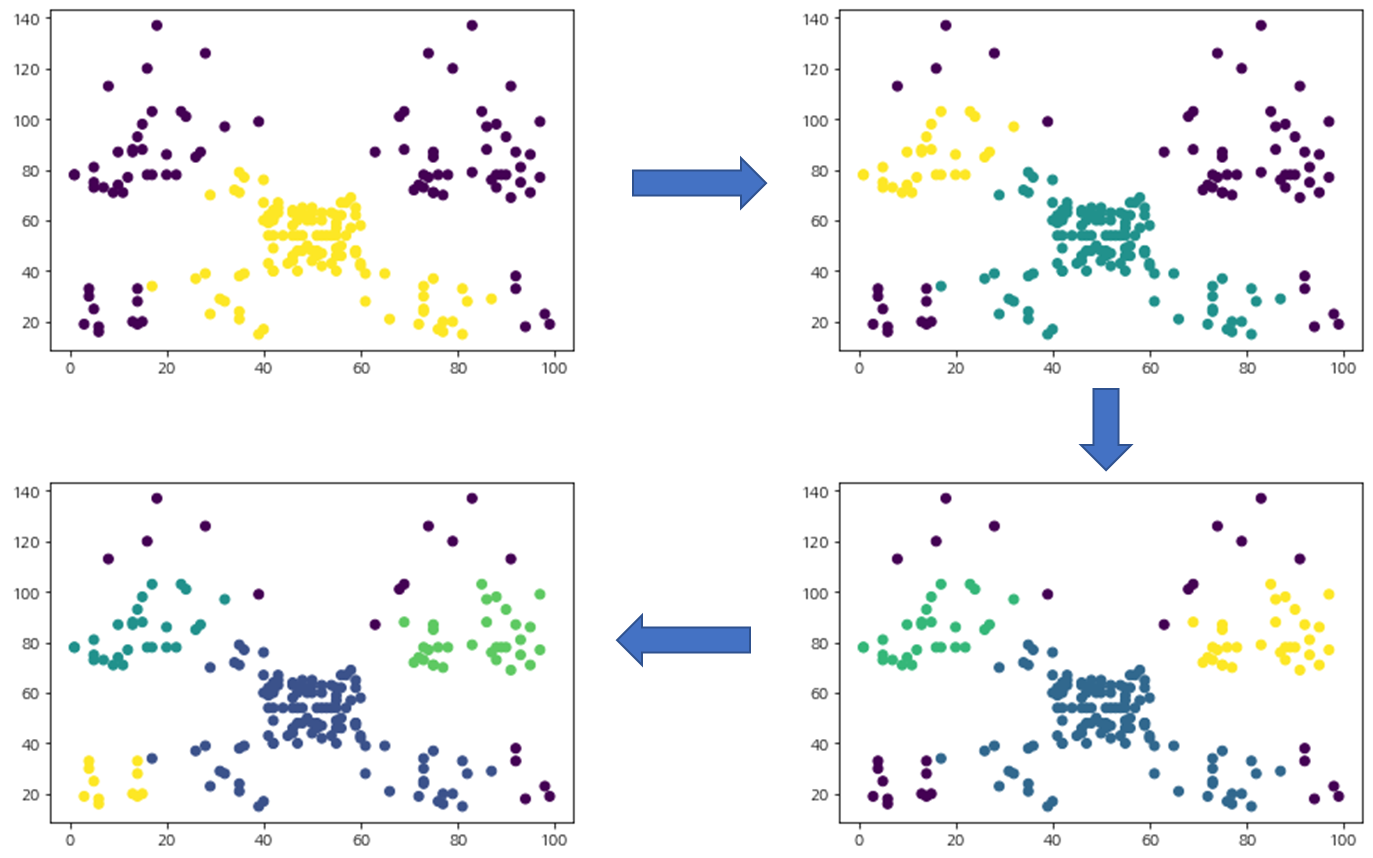
다음으로 Scikit-Learn에서 제공하는 DBSCAN 클래스를 이용하여 클러스터를 할당해보았다. DBSCAN 클래스를 초기화할 때 반경 eps, 최소 샘플 수 min_samples를 설정한 뒤 fit 메서드를 호출하여 클러스터링을 수행한다.
from sklearn.cluster import DBSCAN
clustering = DBSCAN(eps=10, min_samples=5).fit(X)
fig = plt.figure()
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(df['Spending_Score'], df['Annual_Income'], c=clustering.labels_)
plt.show()
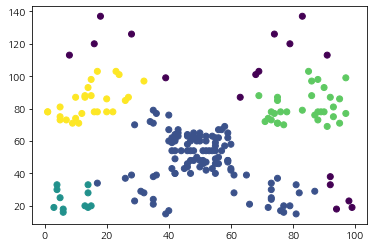
결과가 일치했다. 근데 이상한 건 클러스터링 속도가 내 것이 더 빨랐다. 내가 구현한 것의 실행 속도는 117ms이고 DBSCAN은 4.62초가 걸렸다. 아무래도 DBSCAN은 좀 더 일반적인 데이터까지 클러스터링을 잘할 수 있게 설계되어서 그럴 수도 있다.
이번 포스팅에서는 DBSCAN 알고리즘에 대한 개념을 알아보고 파이썬(Python)으로 구현하는 방법까지 알아보았다. 이번 기회를 통해 DBSCAN 알고리즘이라는 것을 알게 되었고 이를 통해 이상치까지 감지할 수 있음을 알게 되어 그 활용성이 뛰어나다는 점에서 감명받았다. 세상은 넓고 좋은 것은 많으며 공부는 끝이 없음을 다시 한번 느낀다.





댓글