오늘은 기존 연속형 변수에서만 작동하는 K-Means 클러스터링이나 Gaussian Mixture Model 클러스터링과는 달리 범주형 변수에 대한 군집화 기법인 K-Modes Clustering(클러스터링, 군집화)에 대해서 알아보려고 한다. 또한 파이썬(Python) 구현 방법을 알아보고 클러스터링(군집화) 알고리즘을 실제 데이터에 적용해보자.
이번 포스팅에서 다루는 내용은 다음과 같다.
- 목차 -
1. K-Modes Clustering(클러스터링, 군집화) 정의
2. K-Modes Clustering(클러스터링, 군집화) 알고리즘
3. K-Modes Clustering(클러스터링, 군집화) 장단점
K-Means 클러스터링에 대한 내용이 궁금한 분들은 아래 포스팅을 참고하기 바란다. K-Modes 클러스터링을 이해하는데도 어느 정도 도움이 된다.
11. K-Means 클러스터링(Clustering, 군집화)에 대해서 알아보자 with Python
11. K-Means 클러스터링(Clustering, 군집화)에 대해서 알아보자 with Python
이번 포스팅에서는 클러스터링(Clustering, 군집화)의 대표적인 알고리즘 중에 하나로 K-Means 클러스터링에 대해서 알아보려고 한다. 여기서 다루는 내용은 다음과 같다. 1. K-Means 클러스터링(Clusterin
zephyrus1111.tistory.com
이곳은 꽁냥이가 머신러닝을 공부한 내용을 정리하는 곳입니다.
이 포스팅에서는 수식을 포함하고 있습니다. 티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니 웹브라우저 또는 모바일 웹브라우저로 보시길 바랍니다.
1. K-Modes Clustering(클러스터링, 군집화) 정의
K-Modes Clustering(클러스터링, 군집화)는 K-Means 클러스터링과 같은 비지도 학습 알고리즘으로 사전에 클러스터 개수 $k$와 초기값을 입력하면 각 데이터의 그룹을 할당해 나가는 Hard Clustering 알고리즘이다.
다만 K-Means 클러스터링은 연속형 변수를 다루는 반면 K-Modes 클러스터링은 범주형 변수에 대한 군집화 기법이며 클러스터(Cluster)의 중심치를 평균이 아닌 Mode로 계산한다는 차이가 있다.
2. K-Modes Clustering(클러스터링, 군집화) 알고리즘
1) 알고리즘
범주형 데이터 $x_i = (x_{i1}, x_{i2}, \ldots, x_{ip}), i=1, \ldots, n$가 있다고 할 때, K-Modes Clustering(클러스터링, 군집화) 알고리즘은 다음과 같다.
Algorithm
1 단계) 먼저 최대 스텝 수 $M$과 클러스터 개수 $k(<n)$ 를 설정한다.
2 단계) (a)~(b) 단계를 반복한다.
(a) 초기 단계에서는 각 클러스터의 중심치를 데이터에서 $k$개를 랜덤하게 선택한다. 초기 단계가 아닌 경우에는 각 클러스터의 중심치를 Mode(최빈값)을 사용하여 업데이트한다. 동률 발생 시에는 랜덤하게 선택한다.
(b) 모든 데이터 $x_i(i=1, \ldots, n)$에 대하여 클러스터를 할당한다. 이때 유사도가 가장 높은 반대로 말하면 비유사도가 가장 작은 클러스터에 할당한다. 동률 발생 시에는 랜덤하게 선택하여 클러스터를 할당한다. 이때 이전 클러스터링 할당 결과와 일치한다면 알고리즘을 종료한다.
비유사도를 측정하는 기본적인 측도 $d$는 다음과 같다.
$$d(x, y) = \sum_{j=1}^pI(x_j\neq y_j)$$
(c) 최대 스텝 수 $M$에 도달했으면 알고리즘을 종료하고 아닌 경우에는 (a)로 돌아간다.
2) 예제
예를 통하여 K-Modes 클러스터링 알고리즘을 이해해보자.
먼저 다음과 같이 8명 학생에 대한 취미, 좋아하는 과목, 성별 데이터가 있다고 하자.

1 단계) 먼저 최대 스텝 수 $M$과 클러스터 개수 $k(<n)$ 를 설정한다.
먼저 최대 스텝 수는 $M$은 10, 클러스터 개수 $k$를 3개로 설정한다.
2 단계) (a)~(b) 단계를 반복한다.
(a) 초기 단계에서는 각 클러스터의 중심치를 데이터에서 $k$개를 랜덤하게 선택한다. 초기 단계가 아닌 경우에는 각 클러스터의 중심치를 Mode(최빈값)을 사용하여 업데이트한다. 동률 발생 시에는 랜덤하게 선택한다.
여기서 학생 1, 7, 8을 랜덤하게 선택했다.

(b) 모든 데이터 $x_i(i=1, \ldots, n)$에 대하여 클러스터를 할당한다. 이때 유사도가 가장 높은 반대로 말하면 비 유사도가 가장 작은 클러스터에 할당한다. 동률 발생 시에는 랜덤하게 선택하여 클러스터를 할당한다. 이때 이전 클러스터링 할당 결과와 일치한다면 알고리즘을 종료한다.
먼저 첫 번째 학생과 첫 번째 클러스터 중심과의 비 유사도를 계산해보자.
이때 클러스터 중심 $c_1=$(게임, 수학, 남자)과 첫 번째 학생 데이터 $x_1=$(게임, 수학, 남자)의 비유사도를 계산하면 다음과 같다.

$$d(x_1, c_1) = \sum_{j=1}^3I(x_{1j}=c_{1j}) = 0+0+0=0$$
이번엔 클러스터 첫 번째 중심 $c_1=$(게임, 수학, 남자)과 두 번째 학생 $x_2=$(영화, 국어, 여자)의 비유사도를 계산해보자.
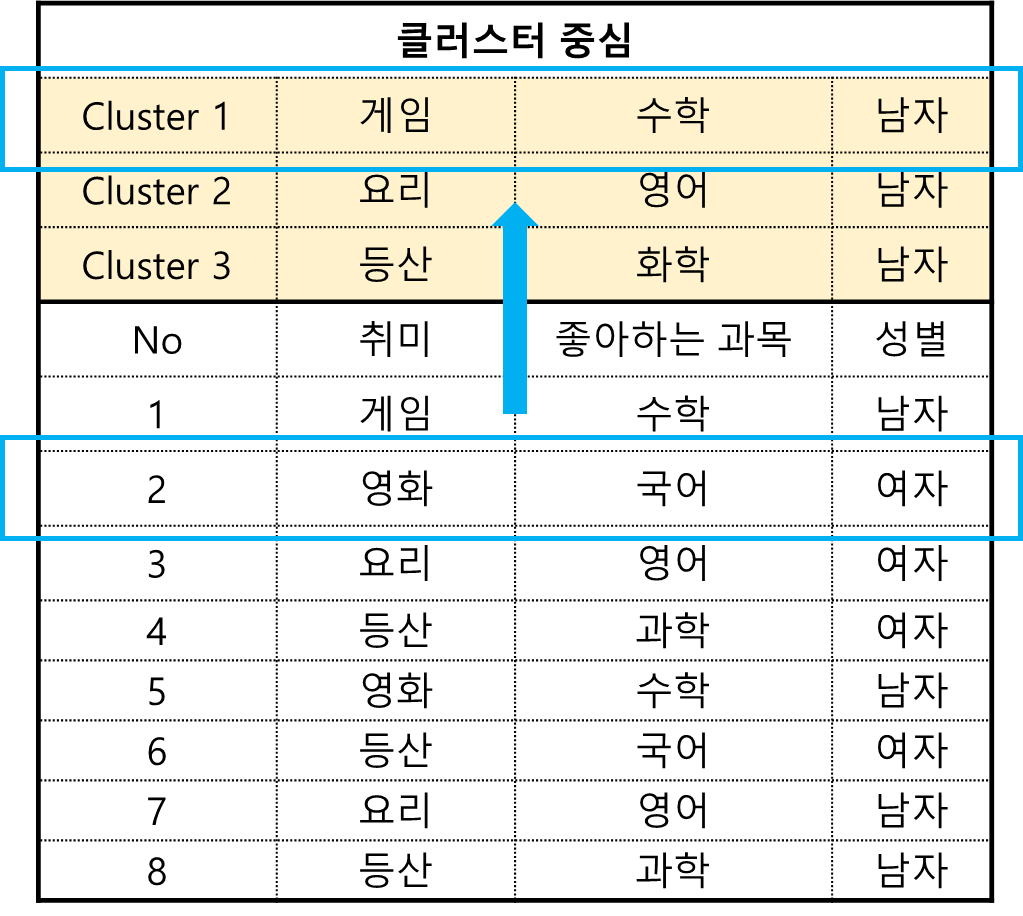
$$d(x_2, c_1) = \sum_{j=1}^3I(x_{2j}=c_{1j}) = 1+1+1=3$$
이제 모든 데이터와 모든 클러스터 중심에 대해서 비 유사도를 계산했으면 각 데이터에 클러스터를 할당한다. 이때 비유사도가 가장 적은 클러스터를 할당한다. 다음은 데이터와 클러스터 중심 간 비 유사도를 계산한 것이며 색칠된 칸은 각 데이터에 대하여 비 유사도가 가장 작은 클러스터를 나타낸 것이다. 이때 두 번째 학생의 경우에는 비 유사도가 모두 3이므로 이 중 랜덤하게 Cluster 1을 선택하였다.

(c) 최대 스텝 수 $M$에 도달 하거나 클러스터링 결과가 달라지지 않았다면 알고리즘을 종료하고 그렇지 않으면 (a)로 돌아간다.
아직 최대 스텝 수에 도달하지 않았으므로 다시 (a) 단계로 돌아간다. 초기 단계가 아니므로 Mode를 사용하여 클러스터 중심치를 업데이트 한다. 아래 그림은 할당된 클러스터를 바탕으로 중심치를 업데이트 한 것이다.

이제 (b) 단계로 가서 클러스터링을 비유사도 기반으로 클러스터링을 할당한다.

이전 클러스터 할당 결과와 동일하므로 알고리즘을 종료한다.
3. K-Modes Clustering(클러스터링, 군집화) 장단점
- 장점 -
a. 범주형 변수를 다룰 수 있다.
b. 구현이 쉽다.
K-Modes 클러스터링 알고리즘은 K-Means와 같이 클러스터 할당 그리고 중심치 업데이트로 이루어진 단순한 구조이므로 구현하기 쉽다.
- 단점 -
a. 초기 중심치에 민감하다.
초기 중심치에 따라 결과가 매우 달라질 수 있고 초기 중심치를 랜덤으로 뽑다 보니 바로 다음 스텝에서 알고리즘이 조기 종료될 가능성이 있다. 따라서 이를 방지하기 위해 초기 중심치 후보를 여러 개 뽑고 이 중에서 가장 작은 비용 함수를 갖는 중심치를 최초 클러스터 중심으로 설정하게 된다. 이때 비용 함수는 보통 각 클러스터의 비 유사도 합을 사용한다.
b. Global한 최적 클러스터 결과를 보장하지 않는다.
모든 클러스터 중심치 후보군 $nC_k$를 고려하는 것이 아니므로 Global한 최적 클러스터 결과를 보장하지 않는다.
c. 이상치에 민감하다.
여기서 말하는 이상치는 클러스터 중심치와의 비 유사도가 큰 데이터를 말한다. 이는 보통 빈도수가 적은 범주형 변수가 포함된 경우의 이상치가 될 가능성이 많으며 K-Modes 클러스터링 알고리즘은 이러한 이상치 데이터로 인하여 예상치 못한 클러스터링 결과가 발생할 수 있다.
4. 파이썬(Python) 구현
먼저 K-Modes 클러스터링 알고리즘을 적용할 데이터를 만들어주었다.
import pandas as pd
import numpy as np
df = pd.DataFrame()
df['취미'] = ['게임', '영화', '요리', '등산', '영화', '등산', '요리', '등산']
df['과목'] = ['수학', '국어', '영어', '과학', '수학', '국어', '영어', '과학']
df['성별'] = ['남자', '여자', '여자', '여자', '남자', '여자', '남자', '남자']
df
이제 K-Modes 클러스터링 알고리즘을 구현해보자. 여기서는 파이썬(Python)으로 직접 구현하는 방법과 kmodes 모듈을 이용한 방법을 알아보자.
1) 직접 구현
아래 코드는 K-Modes 클러스터링 알고리즘을 수행하는 KModesAlgorithm 클래스를 정의한 것이다. 이 클래스는 클러스터 개수 k, 최대 스텝 수 max_step, 초기 클러스터 도출 횟수 n_iter, 랜덤 재생성을 위한 시드 숫자 random_state, 초기 클러스터 중심 인덱스 init_cci를 인자로 받는다.
그리고 매트릭스에서 칼럼별로 최빈값(Mode)을 계산하는 get_mode, 범주를 숫자로 바꾸는데 필요한 cat_to_num, 비 유사도를 계산하는 dissimilarity, 실제로 클러스터링을 수행하는 fit, 클러스터를 할당하는 predict 함수를 정의했다.
class KModesAlgorithm():
def __init__(self, k, max_step=5, n_iter=5, random_state=100, init_cci=None):
self.k = k ## 클러스터 개수
self.max_step = max_step ## 최대 스텝 수
self.n_iter = n_iter ## 초기 클러스터 중심 샘플링 횟수
self.random_state = random_state ## 랜덤 시드
self.X_categorized = None ## 숫자로 범주화된 데이터
self.cluster_center = None ## 최종 클러스터 중심
self.cat_map_dict = None ## 범주를 숫자로 바꾸기 위한 딕셔너리
self.predicted_cluster = None ## 최종 할당 클러스터
self.init_cci = init_cci ## 초기 클러스터 인덱스
def get_mode(self, x):
return np.bincount(x).argmax()
def cat_to_num(self, X):
num_feature = X.shape[1]
cat_map_dict = dict()
for i in range(num_feature):
uniq_val = np.unique(X[:,i])
cat_to_num = dict()
num_to_cat = dict()
for j, uv in enumerate(uniq_val):
cat_to_num[uv] = j
num_to_cat[j] = uv
cat_map_dict[i] = [cat_to_num, num_to_cat]
self.cat_map_dict = cat_map_dict
def dissimilarity(self, x, y):
return np.sum(x!=y)
def fit(self, X):
is_fitting = True
X = X.copy()
self.cat_to_num(X)
k = self.k
## category to num
for i in range(X.shape[1]):
col_cat_map = self.cat_map_dict[i][0]
X[:, i] = list(map(lambda x: col_cat_map[x], X[:, i]))
X = X.astype(np.int64)
self.X_categorized = X
## choose initial cluster center
if self.init_cci is None:
np.random.seed(self.random_state)
obj_val = np.infty
for _ in range(self.n_iter):
cluster_center_idx = np.random.choice(range(X.shape[0]), size=k, replace=False)
## Assign Cluster
cluster_center = X[cluster_center_idx, :]
predicted_cluster = self.predict(X, cluster_center, is_fitting)
cur_val = 0
for i, pc in enumerate(predicted_cluster):
cur_val += self.dissimilarity(X[i:], cluster_center[pc])
if cur_val < obj_val:
obj_val = cur_val
opt_cci = cluster_center_idx
self.init_cci = cluster_center_idx
## Apply Algorithm
step = 1
cur_cluster_center = X[self.init_cci, :]
cur_predicted_cluster = self.predict(X, cur_cluster_center, is_fitting)
while step <= self.max_step:
## Update Center
next_cluster_center = []
for c in np.unique(cur_predicted_cluster):
c_idx = np.where(cur_predicted_cluster == c)[0]
temp_cluster_center = np.apply_along_axis(self.get_mode, 0, X[c_idx,:])
temp_cluster_center = temp_cluster_center.tolist()
next_cluster_center.append(temp_cluster_center)
next_cluster_center = np.array(next_cluster_center)
## Assign Cluster
next_predicted_cluster = self.predict(X, next_cluster_center, is_fitting)
## Stop Criterion
if len(np.unique(next_predicted_cluster)) != k:
self.predicted_cluster = cur_predicted_cluster
self.cluster_center = cur_cluster_center
break
if all(cur_predicted_cluster == next_predicted_cluster):
self.predicted_cluster = cur_predicted_cluster
self.cluster_center = cur_cluster_center
break
else:
cur_cluster_center = next_cluster_center
cur_predicted_cluster = next_predicted_cluster
step += 1
self.predicted_cluster = next_predicted_cluster
self.cluster_center = next_cluster_center
return self
## Assign Clusters
def predict(self, X, cluster_center=None, is_fitting=False):
if is_fitting:
return np.array([self._predict(x, cluster_center) for x in X])
else:
for i in range(X.shape[1]):
col_cat_map = self.cat_map_dict[i][0]
X[:, i] = list(map(lambda x: col_cat_map[x], X[:, i]))
X = X.astype(np.int64)
return np.array([self._predict(x, cluster_center) for x in X])
def _predict(self, x, cluster_center=None, is_fitting=False):
if cluster_center is None:
cluster_center = self.cluster_center
return np.argmin([self.dissimilarity(x, cc) for cc in cluster_center])
이제 코드를 구현했으니 테스트를 해보자. 이때 앞의 예제에서 살펴보았던 것과 동일한 결과를 얻는지 살펴보기 위해 초기 클러스터를 1, 7, 8 데이터로 사용했다.
X = df.values ## 데이터
my_kmodes = KModesAlgorithm(k=3, init_cci=[0, 6, 7]).fit(X) ## 클래스 초기화 및 클러스터링
print(my_kmodes.predict(X)) ## 최종 클러스터

예제에서 살펴보았던 결과와 동일한 결과를 얻었다.
2) kmodes 모듈
이번엔 kmodes 모듈을 사용하여 클러스터링을 해보자.
kmodes에서 제공하는 KModes는 클러스터 개수 n_clusters를 설정한다. 또한 위와 동일한 결과를 확인하기 위해 init 인자에 초기 클러스터 중심치를 설정하였다. 이때 원 데이터는 문자형이므로 이를 숫자로 코딩한 데이터를 사용하여 초기 중심치를 설정했다.
KModes 클래스 초기화후 fit을 통해 클러스터링을 수행하며 predict를 통해 클러스터를 할당한다.
from kmodes.kmodes import KModes
X_categorized = my_kmodes.X_categorized ## 숫자화된 데이터
kmodes = KModes(n_clusters=3, init=X_categorized[[0,6,7],:]) ## 클래스 초기화
kmodes.fit(X) ## 클러스터링 수행
print(kmodes.predict(X)) ## 클러스터 할당

내가 구현한 것과 동일한 결과를 얻을 수 있었다. 짝짝~!!
이번 포스팅에서는 범주형 변수의 특화된 K-Modes 클러스터링 알고리즘의 개념과 구현 방법을 알아보았다. 구현은 단순했지만 복잡했으나 그래도 잘 완성돼서 뿌듯했다.
- 참고자료 -
KModes Clustering Algorithm for Categorical Data - https://www.analyticsvidhya.com/blog/2021/06/kmodes-clustering-algorithm-for-categorical-data/

'통계 > 머신러닝' 카테고리의 다른 글
| 30. DBSCAN에 대해서 알아보자 with Python (0) | 2022.11.03 |
|---|---|
| 29. Piecewise Polynomial(Constant, Linear) Regression에 대해서 알아보자 with Python (6) | 2022.10.20 |
| 27. Partial Dependence Plot (부분 의존도 그림), Individual Conditional Expectation Plot (개별 조건부 평균 그림)에 대해서 알아보자 with Python (0) | 2022.09.02 |
| 26. 변수 중요도(Variable Importance) with Python (0) | 2022.08.27 |
| 25. Shapley Value와 SHAP에 대해서 알아보자 with Python (19) | 2022.08.25 |





댓글