이번 포스팅에서는 머신러닝 예측 모형의 해석을 도와주는 시각화 방법인 Partial Dependence Plot (부분 의존도 그림), Individual Conditional Plot (개별 조건부 평균 그림)에 대해서 소개한다. 또한 파이썬을 이용한 구현 방법을 소개한다.
- 목차 -
2. Individual Conditional Expectation Plot
1. Partial Dependence Plot(부분 의존도 그림)
1) 정의
Partial Dependence Plot (부분 의존도 그림)은 학습된 예측 모형과 (예측에 사용된) 개별 변수의 관계를 시각화한 그림이다.
위의 말을 자세히 뜯어보자.
부분 의존성? 그게 뭐야?
부분 의존성은 다변수 함수에서 관심의 대상이 되는 변수 외에 다른 변수들은 모두 고정시켜놓고 관심 변수에 따른 다변수 함수의 영향성을 말한다. 다시 말해 전체 변수에 의존하는 다변수 함수를 관심의 대상이 되는 부분 변수에 의존하는 함수, 즉 부분 의존 함수로 바꾸었을때 그 영향성이라고 생각하면 된다. 그리고 부분 의존성 그림(Partial Dependence Plot)은 관심 변수에 대한 부분 의존 함수의 부분 의존성을 시각화한 그림인 것이다.
수식을 덧붙여보자. 먼저 설명 변수 벡터 $x = (x_1, \ldots, x_p)$와 예측 모형 $f$가 있다고 하자. $f$는 $x$의 함수이다. 이제 관심 대상 변수를 $x_j$라 해보자. 그리고 $f$를 $x$가 아닌 $x_j$에만 의존하는 부분 의존 함수 $f_j(x_j)$를 만들었다고 해보자. 부분 의존성 그림은 $x_j$에 따른 $f_j(x_j)$의 변화를 나타내는 그림이라는 것이다.
부분 의존성 그거 어떻게 구해?
관심의 대상이 되는 변수 인덱스 집합을 $S$, 나머지는 $S^c$라 하자. 그렇다면
$$f(x) = f(x_S, x_{S^c})$$
로 표현할 수 있다. 부분 의존성 그림을 그리기 위해선 $f$를 $x_S$에 의존하는 부분 의존 함수로 바꿔줘야한다. 이때 사용하는 것이 $x_S$가 주어졌을 때 $f$의 조건부 기대값이다.
이제 $f_S(x_S)$는 다음과 같이 $x_S$가 주어진 경우의 $f(x)$의 조건부 기대값을 고려한다.
$$f(x_S) = E(f(x_S, X_{S^c})|x_S) = \int f(x_S, x_{S^c})p(x_{S^c}|x_S) dx_{S^c} \tag{1}$$
(1)에서 중요한 건 조건부 확률 밀도 함수 $p(x_{S^c}|x_S)$를 모른다는 것이다. 이때 데이터 샘플을 이용하여 $p(x_{S^c}|x_S)$를 근사하는 방법이 있다. 근사를 위한 데이터는 보통 학습 데이터나 검증 데이터를 사용한다.
학습 데이터 $(x_i, y_i), i=1, \ldots, n$이 있고 이를 이용하여 학습된 예측 모형을 $f$라 하자. 여기서 $x_i = (x_{i1}, \ldots, x_{ip})$는 $p$ 차원 벡터이고 $y_i$는 숫자 또는 범주형 변수이다.
여기서 문제는 학습 데이터를 이용해도 조건부 확률 밀도 함수를 근사하기 어렵다는 것이다. 왜냐하면 $x_S$가 데이터에 포함되어 있을지도 미지수이며(연속형이 포함되어 있는 경우를 생각해보자) 설령 있다고 하더라도 $x_S$로 한정시키게 되면 조건부 확률 밀도 함수를 계산할 수 있는 샘플수가 급격히 감소하여 제대로 근사를 할 수 없기 때문이다(아래 그림 참고).
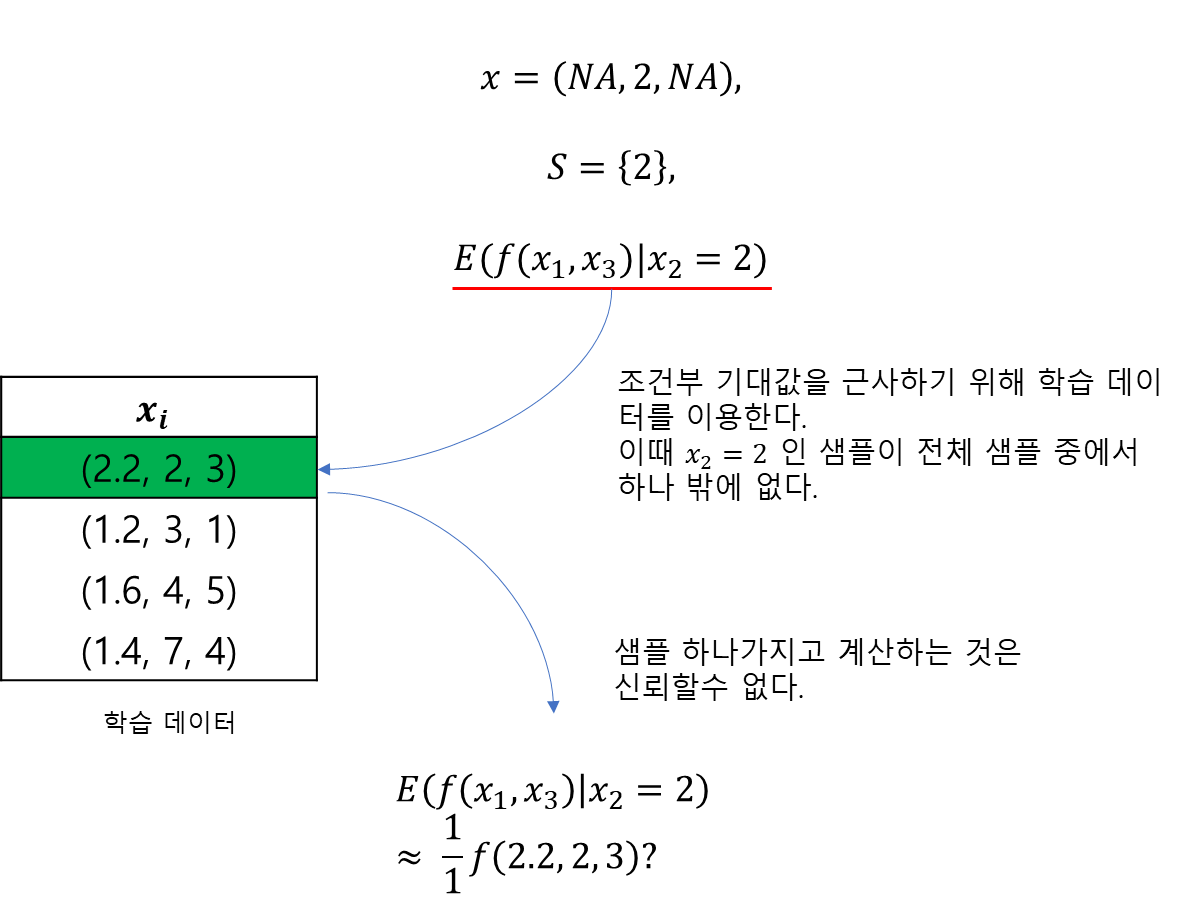
따라서 근사의 신뢰성을 확보하기 위하여 변수 간의 독립성을 가정하게 된다. 즉,
$$p(x_{S^c}|x_S) = p(x_{S^c})$$
이 된다. 이것이 Marginalization인 것이다. 이를 (1)에 적용하면 다음과 같다.
$$f_S(x_S) = \int f(x_S, x_{S^c})p(x_{S^c}) dx_{S^c} (\approx E(f(x_S, X_{S^c})|x_S)) \tag{2}$$
물론 정확한 $ p(x_{S^c})$를 모르지만 대신 샘플 수를 데이터의 개수까지 사용할 수 있다는 것이다. 만약 학습 데이터를 통해 (2)를 근사한다고 해보자. 전체 데이터에서 랜덤 추출(샘플링)된 $k$개 행(row)들을 $x_{r_1}, \ldots, x_{r_k}$라 하자. 그렇다면 $x_{r_i}$에 있는 변수들은 $S$에 포함되거나 안되거가 둘 중 하나일 것이다. 즉,
$$x_{r_i} = (x_{r_i, S}, x_{r_i, S^c})$$
이제 주어진 $x_S$에 대하여 $x_{S^c}$를 학습 데이터에서 샘플링된 것으로 대체한 뒤 (2)를 다음과 같이 계산한다(정확히 말하면 학습 데이터로 근사하는 것이다).
$$ f_S(x_S) = \frac{1}{k}\sum_{i=1}^kf(x_S, x_{r_i, S^c}) (\approx \int f(x_S, x_{S^c})p(x_{S^c}) dx_{S^c}) \tag{3}$$
다음은 부분 의존 함수 $f_S(x_S)$를 계산하는 과정이다.

부분 의존성 그림(Partial Dependence Plot)은 보통 하나 또는 두 개 변수 $x_j(j=1, \ldots, p)$에 대한 부분 의존 함수 $f_{j}(x_j)$의 변화를 보는 것이다. 이제 다음 섹션에서 구현하는 방법을 알아보자.
2) 파이썬 구현
a. 직접 구현
먼저 필요한 모듈을 임포트하고 데이터는 보스턴 집값 데이터를 사용한다. 예측 모형은 랜덤 포레스트로 정했고 이를 학습해주었다.
import pandas as pd
import numpy as np
from sklearn.inspection import PartialDependenceDisplay
from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor
## 보스턴 데이터
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['MEDV'] = boston.target
X = df[['AGE', 'RAD', 'TAX', 'DIS', 'RM', 'LSTAT', 'B', 'INDUS', 'CHAS']].values
y = df['MEDV'].values
## 예측 모형 모형 적합
model = RandomForestRegressor(max_depth=4, random_state=0).fit(X, y)
다음은 부분 의존 그림(Partial Dependence Plot)을 그리는 함수이다. 이 함수는 학습된 모델(model), 부분 의존 함수 값을 계산할 데이터(data), 관심 대상 변수 인덱스(feature_idx) 그리고 변수 이름(feature_names)으로 받는다.
먼저 특정 변수 칼럼을 선택(x)하고 해당 칼럼의 모든 값(val)을 돌면서 나머지 칼럼은 data와 같고 해당 칼럼은 모두 val로 바꿔준다. 그러고 나서 학습된 모형(model)을 이용하여 예측값의 평균을 계산하고 이를 avg_predicted_value에 모아준다.
def partial_depedence_plot(model, data, feature_idx, feature_names):
import matplotlib.pyplot as plt
x = sorted(data[:, feature_idx]) ## 관심 대상 변수 칼럼 추출
avg_predicted_value = []
for val in x:
data_rep = data.copy()
data_rep[:, feature_idx] = val
avg_predicted_value.append(np.mean(model.predict(data_rep))) ## 부분 의존 함수 값
## 시각화
fig = plt.figure(figsize=(8, 8))
fig.set_facecolor('white')
ax = fig.add_subplot()
plt.plot(x, avg_predicted_value)
plt.xlabel(feature_names[feature_idx])
plt.ylabel('Partial Dependency')
plt.show()
함수를 만들었으니 테스트를 해보자.
data = X
feature_idx = 1
partial_depedence_plot(model, data, feature_idx, boston.feature_names)
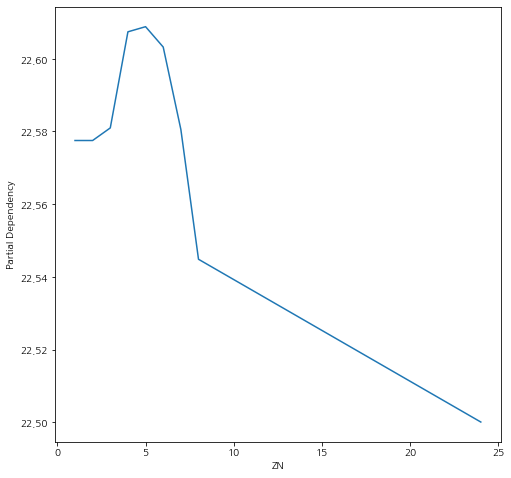
b. Scikit-Learn 사용
Scikit-Learn에서는 PartialDependenceDisplay을 사용하여 부분 의존 그림(Partial Dependence Plot)을 그릴 수 있다.
fig = plt.figure(figsize=(8, 8))
fig.set_facecolor('white')
ax = fig.add_subplot()
PartialDependenceDisplay.from_estimator(model, X, [1], ax=ax)
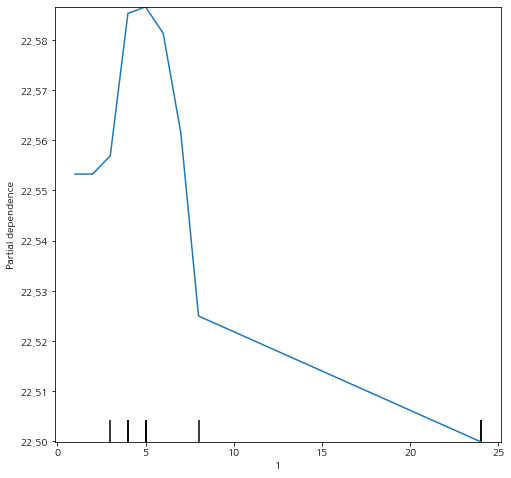
앞서 구현한 것과 동일한 결과를 얻을 수 있다. 다만 속도는 PartialDependenceDisplay가 훨씬 빠르다. ㄷㄷ;;
3) 장단점
- 장점 -
a. 구현이 매우 쉽다.
특정 변수에 대한 부분 의존 값을 계산만 하면 끝난다. 그 계산 또한 평균을 이용하면 되므로 구현이 매우 쉽다.
b. 직관적인 해석을 제공한다.
특정 변수에 대한 예측 모형의 변화를 직관적으로 알 수 있다.
c. 모형 클래스의 상관없이(Model-Agnostic) 적용할 수 있다.
- 단점 -
a. 계산량은 많다.
변수 자체가 많고 또한 변수 내 유니크한 값이 많아질수록 계산량은 증가한다.
b. 특정 변수값에 사실 부분 의존 함수 계산을 위한 데이터 개수만큼의 예측값이 하나의 평균으로 대체되므로 그 분포를 알 수없어 신뢰도가 저하된다.
c. 시각화할 수 있는 변수의 최대 개수는 2개로 한정된다.
2. Individual Conditional Expectation Plot(개별 조건부 평균 그림)
1) 정의
Individual Conditional Expectation Plot(ICE, 개별 조건부 평균 그림)은 특정 변수에 대한 의존도를 개별 예측치로 시각화한 것이다.
먼저 학습 데이터 $(x_i, y_i), i=1, \ldots, n$이 있고 이를 이용한 예측 모형을 $f$라 하자. 여기서 $x_i = (x_{i1}, \ldots, x_{ip})$는 $p$ 차원 벡터이고 $y_i$는 숫자 또는 범주형 변수이다. 이때 ICE는 관심의 대상이 되는 변수 집합 $x_S$에 대하여 다음을 계산한다.
$$f_S(x_S)^i = f(x_S, x_{S^c}^i), i=1, \ldots, n$$
여기서 $x_{S^c}^i$는 $S$에 포함되지 않는 칼럼으로 이루어진 행렬에서 $i$번째 행을 의미한다.
ICE Plot은 $x_S$에 대한 $f_S(x_S)^i$를 모든 $i$에 대해서 그린 것이다.
ICE Plot은 부분 의존성 그림(Partial Dependence Plot)의 단점인 개별 예측값의 분포를 고려하지 못한다는 점을 보완하기 위해 제안된 것이다. ICE는 학습 데이터를 이용하여 의존도를 계산한다면 그 개수만큼의 선이 그려진다는 특징이 있으며 이러한 선의 평균을 그리면 부분 의존성 그림과 같아진다.
2) 파이썬 구현
a. 직접 구현
아래 코드는 ICE 그림을 그려주는 함수이다. 이 함수의 실행 과정은 부분 의존성 그림에서 구현했던 것과 비슷하다. 다만 예측값의 평균을 사용했던 부분 의존성 그림과는 달리 ICE는 개별 예측값 전체를 사용한다는 차이점이 있다(line 5~10).
def ice_plot(model, data, feature_idx, feature_names):
import matplotlib.pyplot as plt
x = sorted(data[:, feature_idx]) ## 관심 대상 변수 칼럼 추출
individual_dependence = []
for val in x:
data_rep = data.copy()
data_rep[:, feature_idx] = val
individual_dependence.append(model.predict(data_rep)) ## 개별 부분 의존 함수 값
individual_dependence = np.column_stack(individual_dependence)
## 시각화
fig = plt.figure(figsize=(8, 8))
fig.set_facecolor('white')
ax = fig.add_subplot()
for i in range(individual_dependence.shape[0]):
ice = individual_dependence[i]
plt.plot(x, ice, color='k', alpha=0.5)
## 평균선 추가
avg_ice = np.mean(individual_dependence, axis=0)
plt.plot(x, avg_ice, color='r', linewidth = 4)
plt.xlabel(feature_names[feature_idx])
plt.ylabel('ICE')
plt.show()
이제 함수를 테스트해보자.
feature_idx = 3
data = X
ice_plot(model, data, feature_idx, feature_names)
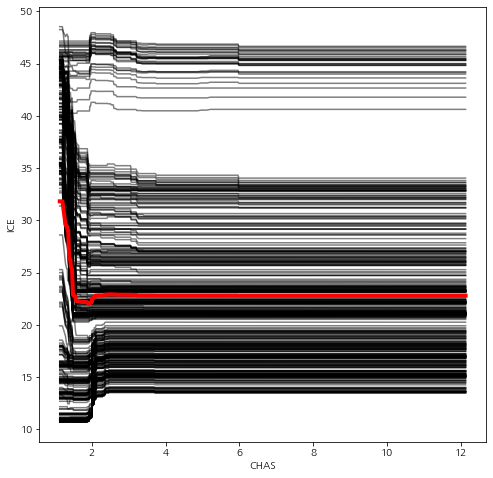
데이터 개수가 500개가 넘어서 그림이 좀 조잡하다. ㄷㄷ;;
b. Scikit-Learn 사용
이번엔 Scikit-Learn에서 제공하는 PartialDependenceDisplay을 사용하여 ICE 그림을 그려보자.
fig = plt.figure(figsize=(8, 8))
fig.set_facecolor('white')
ax = fig.add_subplot()
PartialDependenceDisplay.from_estimator(model, X, [feature_idx], ax=ax, kind='both',
ice_lines_kw = {'color':'k', 'alpha':0.5}, ## ice 선 스타일
pd_line_kw = {'color':'r', 'linewidth':4}, ## 평균선 스타일
)
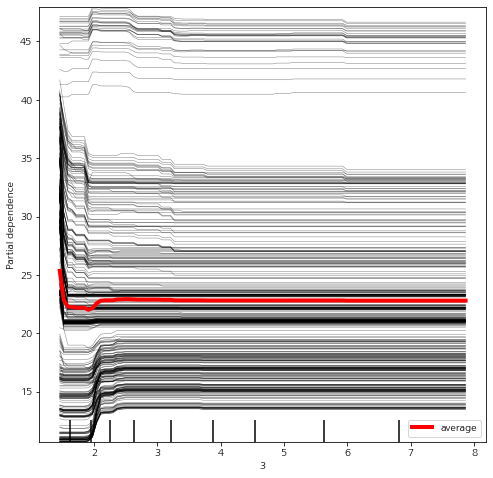
앞부분이 조금 잘렸지만 구현했던 것과 동일하다. 속도는 역시 PartialDependenceDisplay이 빠르다.
3) 장단점
- 장점 -
a. 직관적인 해석 가능
관심 변수에 대한 예측 모형의 변화를 직관적으로 알 수 있다.
b. 예측 모형의 변화를 개별 관측치 별로 볼 수 있으므로 좀 더 신뢰성 있는 해석이 가능하다.
c. 부분 의존성 그림과 마찬가지로 모형 클래스의 상관없이(Model-Agnostic) 적용할 수 있다.
- 단점 -
a. 데이터 수가 많을 경우 그림이 난잡해져서 예측 모형의 변화를 제대로 파악하기 어려움
b. 시각화할 수 있는 관심 대상 변수의 개수가 한정적이다(1개 또는 2개).
이번 포스팅에서는 Partial Dependence Plot (부분 의존도 그림), Individual Conditional Expectation Plot (개별 조건부 평균 그림)에 대한 개념과 파이썬 구현 방법을 알아보았다. 이게 잘 사용되지는 않지만 블랙박스라 일컬어지는 머신러닝 모형에 대한 해석을 시각적으로 표현했다는 점에서 큰 의의가 있는 그림들이다. 특히 부분 의존성 계산 방법은 SHAP과 같은 최신 해석 방법에서 사용되는 것이므로 알아두면 좋다.
- 참고 자료 -
8.1 Partial Dependence Plot (PDP) - https://christophm.github.io/interpretable-ml-book/pdp.html
9.1 Individual Conditional Expectation (ICE) - https://christophm.github.io/interpretable-ml-book/ice.html
An Overview of Model-Agnostic Interpretation Methods - 고려대 DMQA 세미나
'통계 > 머신러닝' 카테고리의 다른 글
| 29. Piecewise Polynomial(Constant, Linear) Regression에 대해서 알아보자 with Python (6) | 2022.10.20 |
|---|---|
| 28. K-Modes Clustering(클러스터링, 군집화)에 대해서 알아보자 with Python (383) | 2022.09.04 |
| 26. 변수 중요도(Variable Importance) with Python (0) | 2022.08.27 |
| 25. Shapley Value와 SHAP에 대해서 알아보자 with Python (19) | 2022.08.25 |
| 24. 랜덤 포레스트(Random Forest)에 대해서 알아보자 (3) | 2022.08.05 |





댓글