이번 포스팅에서는 Gradient Boosting의 개념과 알고리즘을 소개하며 이를 응용한 Gradient Tree Boosting의 개념과 알고리즘도 소개한다. 그리고 Gradient Tree Boosting 알고리즘을 파이썬으로 직접 구현하는 방법을 소개한다. 이렇게 구현한 것을 실제 데이터에 적용하는 예제를 살펴보고 Scikit-Learn에서 제공하는 결과와 비교해보고자 한다.
이 글을 읽기 전에 의사결정나무와 AdaBoosting 관련 내용을 보고 오기 바란다.
9. 의사결정나무(Decision Tree)에 대해서 알아보자 with Python
15. AdaBoost(Adaptive Boost) 알고리즘에 대해서 알아보자 with Python
- 목차 -
3. Gradient Tree Boosting 알고리즘
본 포스팅에서는 수식을 포함하고 있습니다.
티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니
PC 웹 브라우저 또는 모바일 웹 브라우저에서 보시기 바랍니다.
1. Gradient Boosting이란?
먼저 Gradient Boosting의 정의는 다음과 같다.
Gradient Boosting는 Gradient(또는 잔차(Residual))를 이용하여 이전 모형의 약점을 보완하는 새로운 모형을 순차적으로 적합한 뒤 이들을 선형 결합하여 얻어진 모형을 생성하는 지도 학습 알고리즘이다.
이 말의 의미를 하나하나 살펴보자.
a. Gradient Boosting은 잔차를 이용하여 이전 모형의 약점을 보완한다.
먼저 우리들에게 데이터 $(x_i, y_i), i=1, \ldots, n$가 있다. $x_i$는 $p$차원 벡터, $y_i$는 실수이다(범주형은 정수로 표현될 수 있으므로 여기에 포함된다).
먼저 이전 모형(예측 함수)을 $F_{\text{prev}}$라 하고 개별 입력 변수 $x_i$에 대한 예측값을 $F_{\text{prev}}(x_i)$라 하자. 이전 모형의 약점이라함은 이전 모형이 실제값 $y_i$를 정확하게 예측하지 못한 정도라고 생각하면 된다. 즉, 예측값과 실제값의 차이가 커지면 이전 모형의 약점은 치명적이 된다는 것이다. 이것은 실제값과 예측값의 차이, 즉 잔차와 연결된다.
이전 모형의 약점을 보완하는 것이 Gradient Boosting이라고 했다. 그렇다면 어떻게 보완한다는 것일까? 그것은 바로 실제값과 예측값의 차이를 줄여주는 함수 $h$를 찾는 것이다. 다시말해
$$\begin{align} y_1 &= F_{\text{prev}}(x_1) + h(x_1) \\ y_2 &= F_{\text{prev}}(x_1) + h(x_1) \\ &\vdots \\ y_n &= F_{\text{prev}}(x_n) + h(x_n) \end{align}$$
이렇게 $h$를 찾으면 새로운 예측 함수값은 $F_{\text{new}}(x) = F_{\text{new}}(x)+l h(x)$가 된다. $0< l < 1$이다.
즉, $h(x)$를 그대로 더하는 것이 아니라 상수 $l$을 곱하여 더하게 된다. 이 $l$을 학습률이라고 한다. $l$을 곱해주지 않으면 학습 데이터에 지나치게 적합되므로 과적합 현상이 발생하게 된다. 따라서 $l$을 곱해주어 과적합을 방지한다.
아래에서 이전 모형의 예측값을 빨간 선이라고 해보자(좌측 상단). 그러고 나서 실제값과 예측값의 차이를 줄여주는 $h$를 학습하게 된다.(우측 상단). 이때 새로운 예측값을 $F_{\text{prev}}(x)+h(x)$을 할 수도 있다(우측 하단). 하지만 이 경우 학습 데이터를 과도하게 적합할 수 있기 때문에, 즉 과적합이 발생할 수 있어서 잔차를 많이 줄이는 대신(하지만 이전 모형보다는 잔차는 작아진다) 학습률 $l$을 $h(x)$에 곱한 값을 이전 모형의 예측값에 더하여 새로운 예측값 $F_{\text{new}}(x) = F_{\text{prev}}(x)+l h(x)$를 얻게 된다(좌측 하단 그림).

그렇다면 최적 $h$를 어떻게 찾을까? 이는 뒤에서 설명한다.
b. Gradient Boosting은 순차적으로 적합한 뒤 이들을 선형 결합한 모형을 생성한다.
앞에서 Gradient Boosting은 순차적으로 이전 모형의 약점을 보완하는 모형을 만들게 된다. 순차적으로 적합할 모형 개수를 $m$이라 하자. 첫 번째(시작) 모형의 예측값을 $F_0(x) = h_0(x)$라 하면 최종 모형 $F_m$은 다음과 같이 $h_j$들의 선형 결합으로 만들어진다.
$$F_m(x) = h_0(x)+l h_1(x)+\cdots +lh_m(x)\tag{1}$$
c. Gradient Boosting은 지도 학습 알고리즘이다.
Gradient Boosting은 라벨(또는 종속변수가) 있는 데이터를 학습하고 이를 통해 새로운 데이터의 라벨(또는 종속변수)을 예측하는 지도 학습 알고리즘이다.
2. Gradient Boosting 알고리즘
먼저 Gradient Boosting의 알고리즘을 소개한다. 그러고 나서 회귀 문제에서 적용방법을 알아본 뒤 분류 문제에 적용하는 방법을 예제를 통해 알아본다.
1) 알고리즘
먼저 우리에게 데이터 $(x_i, y_i), i=1, \ldots, n$이 있다. 그리고 미분 가능한 손실 함수 $L(y, F(x))$가 있다고 하자. 실제값($y$)과 예측값($F(x)$)의 차이가 작으면 $L$도 작고 크면 커진다. 개별 모형의 최대 개수를 $M$, 학습률 $l$을 설정한다.
Gradient Boosting 알고리즘은 다음과 같다.
Gradient Boosting Algorithm
1. 초기 모형은 상수로 설정하며 다음과 같이 찾는다.
$$\DeclareMathOperator*{\argminA}{arg\,min} F_0(x) = \argminA_{\gamma} \sum_{i=1}^nL(y_i, \gamma)$$
2. $m=1, \ldots, M$에 대하여 (a)~(d)를 반복한다.
(a) 다음과 같이 유사 잔차(Pseudo Residual)를 계산한다. $$r_{im} = -\left [ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right ]_{F(x)=F_{m-1}(x)} \;\; \text{for}\;\; i=1, \ldots, n$$
(b) 앞에서 구한 잔차를 새로운 종속변수로 하여 기본 학습기(Base Learner, 예: 의사결정나무) $g_m$을 학습한다. 즉, $(x_i, r_{im}), i=1, \ldots, n$을 이용하여 학습하게 된다.
(c) 상수 $\gamma_m$을 다음과 같이 계산한다. $$\DeclareMathOperator*{\argminA}{arg\,min} \gamma_m = \argminA_{\gamma} \sum_{i=1}^nL(y_i, F_{m-1}(x_i)+\gamma g_m(x_i))$$
(d) 모형을 업데이트한다. $$F_m(x) = F_{m-1}(x)+l\cdot \gamma_m\cdot g_m(x) $$
3. 최종 모형은 다음과 같다.
$$F_M(x)$$
2) 알고리즘 고찰
여기서는 Gradient Boosting 알고리즘에서 가정이 필요한 이유와 알고리즘 유도 과정을 설명하려고 한다.
수식만 보면 토가 나오는 사람들은 넘어가도 좋다.
Gradient Boosting 알고리즘이 해결하고자 하는 문제를 일반화시켜보자. 우리는 출력 (확률) 변수 $y$와 $p$차원 입력 변수 벡터 $x$ 손실 함수 $L$에 대하여 다음의 기대손실 함수를 최소화하는 함수 $\hat{F}\in\mathcal{H}$를 찾고 싶은 것이다. 여기서 $\mathcal{H} = \{ F \;|\; F : \mathbb{R}^p \longrightarrow \mathbb{R} \}$이다.
$$\DeclareMathOperator*{\argminA}{arg\,min} \hat{F} = \argminA_{F\in\mathcal{H}}E_{x, y}[L(y, F(x))]$$
근데 $\hat{F}$을 그냥 찾으려고 하면 또 어려운 게 $\mathcal{H}$가 너무 큰 집합이다. 따라서 적절하게 제약을 가해주는데 여기서 말하는 제약은 주어진 자연수 $M$에 대하여 $\mathcal{H}$를 다음과 같이 제약한다는 것이다.
$$H^* = \{F \;|\; F : \mathbb{R}^p \longrightarrow \mathbb{R}, \\ F = \text{const.} + \gamma_1f_1+\cdots+\gamma_Mf_M, \;f_j\in \mathcal{H},\; \gamma_j\in \mathbb{R},\; j=1, \ldots, M \}$$
즉, 일반 함수가 아닌 상수와 여러 함수의 선형 결합으로 표현되는 구조를 추가한 것이다.
또한 우리는 $x, y$의 분포를 모르므로 기대손실을 알 수 없고 유한개의 데이터 $(x_i, y_i), i=1, \ldots, n$를 이용한 경험 손실 함수를 최소화하는 $\hat{F}$를 찾게 된다.
$$\DeclareMathOperator*{\argminA}{arg\,min} \hat{F} = \argminA_{F\in\mathcal{H^*}}\frac{1}{n}\sum_{i=1}^nL(y_i, F(x_i)) \tag{1}$$
(1)은 순차적인 방법을 이용하여 찾게 된다.
$$\DeclareMathOperator*{\argminA}{arg\,min} F_0 = \argminA_{\gamma} \sum_{i=1}^nL(y_i, \gamma)$$
$$\DeclareMathOperator*{\argminA}{arg\,min} F_m = F_{m-1} + \argminA_{f_m\in\mathcal{H}} \sum_{i=1}^nL(y_i,F_{m-1}(x_i)+f_m(x_i))$$
여기서 $1/n$은 최소화하는데 필요 없으므로 지웠다. (위 첫 번째 식은 Algorithm 1.)
이때 Gradient Boosting은 위의 두 번째식을 변형하게 된다. 위에 두 번째식에서 최소화하는 부분은 경사 하강법(Gradient Descent)을 이용한다. 즉, $F_m$을 양수 $\gamma$에 대하여
$$F_m(x) = F_{m-1}(x) - \gamma \sum_{i=1}^n\nabla L(y_i, F_{m-1}(x_i)+f_m(x_i))\tag{2}$$
으로 근사하게 된다. 이 알고리즘의 명칭에 Gradient가 포함되는 이유가 바로 이 부분이다.
여기서
$$\nabla L(y_i, F_{m-1}(x_i)+f_m(x_i)) = \frac{\partial L(y_i, F_{m-1}(x_i)+f_m(x_i))}{\partial f_m(x_i)}\tag{3}$$
하지만 대부분의 경우(제곱 손실 함수를 제외하고) (3)를 직접 계산하기가 까다롭다. 따라서 다음과 같이 1차 Taylor 근사를 $f_m$에 대하여 미분하게 된다. 손실 함수의 미분 가능성이 필요한 이유이다.
$$L(y_i, F_{m-1}(x_i)+f_m(x_i)) \\ \approx L(y_i, F_{m-1}(x_i))+f_m(x_i) \left[ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]_{F(x)=F_{m-1}(x)} \tag{4}$$
(4)의 오른쪽을 $f_m(x_i)$에 대하여 미분하면 (3)의 왼쪽을 다음과 같이 근사할 수 있다.
$$ \frac{\partial L(y_i, F_{m-1}(x_i)+f_m(x_i))}{\partial f_m(x_i)} \approx \left[ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]_{F(x)=F_{m-1}(x)}$$
이를 식(2)에 집어넣으면 다음과 같다.
$$F_m(x) = F_{m-1}(x) - \gamma \sum_{i=1}^n\left[ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]_{F(x)=F_{m-1}(x)}\tag{5}$$
또한 $\gamma$를 다음과 같이 잔차가 작아지도록 최적화할 수 있다.
$$\DeclareMathOperator*{\argminA}{arg\,min} \begin{align} \gamma_m = \argminA_{\gamma >0}\sum_{i=1}^n L \left(y_i, F_{m-1}(x_i) - \gamma \left[ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)}\right]_{F(x)=F_{m-1}(x)}\right) \end{align}\tag{6}$$
이때 다음을 정의한다. (Algorithm 2-(a))
$$r_{im} = -\left [ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right ]_{F(x)=F_{m-1}(x)} \;\; \text{for}\;\; i=1, \ldots, n$$
이를 (6)에 집어넣으면 다음과 같다.
$$\DeclareMathOperator*{\argminA}{arg\,min} \begin{align} \gamma_m = \argminA_{\gamma >0}\sum_{i=1}^n L (y_i, F_{m-1}(x_i) + \gamma r_{im}) \end{align}\tag{7}$$
여기서 한번 더 근사를 하게 되는데 바로 $r_{im}$을 입력 변수 벡터 $x_i$로 잘 근사하는 것이다. 즉, $r_{im}$을 출력 변수로, $x_i$를 입력 변수 벡터로 하여 새로운 함수 $g_m$을 학습하는 것이다(Algorithm 2-(b)). $r_{im}$은 유사 잔차라고 한다(유사 잔차인 이유는 아래에서 설명한다).
이제 $g_m$을 (7)에 집어넣으면 다음과 같다(Algorithm 2-(c)).
$$\DeclareMathOperator*{\argminA}{arg\,min} \begin{align} \gamma_m = \argminA_{\gamma >0}\sum_{i=1}^n L (y_i, F_{m-1}(x_i) + \gamma g_m(x_i)) \end{align}\tag{8}$$
이제 $F_m$은 (5) 대신 과적합 방지를 위한 $l$을 도입하여 다음과 같이 세팅된다(Algorithm 2-(d)).
$$F_m(x) = F_{m-1}(x) + l\cdot \gamma_m\cdot g_m(x)\tag{9}$$
앞에 예에서 $h_j(x), j=1, \ldots, M$는 결국 $\gamma_j\cdot g_j(x)$라고 보면 된다.
3) 생각해볼 점
여기서는 Gradient Boosting 알고리즘에서 생각해볼 점을 몇 자 적어보았다.
(1) 왜 $r_{im}$을 쓰지 않고 이를 근사하여 $g_m(x_i)$를 쓰는가?
$r_{im}$는 학습 데이터에서 $x_i$에 대해서만 계산된 값이다. 하지만 $x_i$ 이외에 다른 값에 대해도 예측해야 하는데 $r_{im}$가지고는 안되니 $r_{im}$과는 비슷하면서 임의의 $x$에 대해서도 유사 잔차를 계산할 수 있는 $g_m$을 도입한 것이다. $r_{im}$과는 비슷해야 하므로 $x_i$를 입력 변수, $r_{im}$을 출력 변수로 하여 $g_m$을 학습하는 것이다.
(2) 왜 수렴 조건을 고려하지 않는가?
Gradient Boosting 알고리즘도 결국 Newton-Raphson 알고리즘처럼 수렴할 때까지 반복할 수 있을 것이다.
즉, 오차한계 $\epsilon >0$을 설정하여
$$ \| F_m-F_{m-1}\| < \epsilon$$
와 같은 수렴조건을 고려할 수 있다. 즉, 위 조건이 만족되면 알고리즘을 종료한다는 것이다. 하지만 이 또한 과적합이 발생할 수 있고 따라서 수렴조건 대신 반복 수 $M$을 정하게 된 것이다.
3. Gradient Tree Boosting 알고리즘
Gradient Boosting 알고리즘에서 각 단계별로 학습하는 $g_m$은 특별한 제약이 없다. 즉, 분류 문제에서는 로지스틱 회귀 모형을 써도 되고 회귀 문제에서는 선형 회귀 모형을 써도 상관없다.
여기서는 $g_m$을 의사결정나무로 학습하는 Gradient Tree Boosting 알고리즘에 대하여 알아보자.
1) 알고리즘
Gradient Tree Boosting 알고리즘은 ($m$번째 스텝에서) 유사 잔차 $r_{im}$을 의사결정나무로 학습한다. 학습을 완료하고 나서 총 끝마디에 개수를 $J_m$라 할때 $j$번째 끝마디에 대한 영역을 $R_{jm}$이라 하자($j=1, \ldots, J_m$).
$(x_i, r_{im}), i=1, \ldots, n$을 이용하여 학습한 의사결정나무 $g_m$은 다음과 같다.
$$g_m(x) = \sum_{j=1}^{J_m}b_{jm}I(x\in R_{jm})$$
여기서 $I$는 지시 함수(Indicator Function)이다.
이를 이용하여 위에서 언급한 Gradient Boosting Algorithm을 수행하게 된다. 위에서 $g_m$을 학습하고 다음 스텝은 상수 $\gamma_m$을 다음과 같이 계산하게 된다.
$$\DeclareMathOperator*{\argminA}{arg\,min} \gamma_m = \argminA_{\gamma} \sum_{i=1}^nL(y_i, F_{m-1}(x_i)+\gamma g_m(x_i))$$
그런 다음 모형을 다음과 같이 업데이트한다.
$$F_m(x) = F_{m-1}(x)+l\cdot \gamma_m\cdot g_m(x) $$
Friedman은 업데이트 방식을 다음과 같이 수정했다.
$$\DeclareMathOperator*{\argminA}{arg\,min} F_m(x) = F_{m-1}(x)+l\sum_{j=1}^{J_m}\gamma_{jm}I(x\in R_{jm}) \\ \gamma_{jm} = \argminA_\gamma \sum_{x_i\in R_{jm}}L(y_i, F_{m-1}(x_i)+\gamma)$$
Friedman이 제안한 Gradient Tree Boosting 알고리즘은 다음과 같다.
Gradient Tree Boosting Algorithm
데이터 $\{(x_i, y_i)\}_{i=1}^n$과 미분 가능한 손실 함수 $L$, 반복수 $M$에 대하여
1. 초기 모형은 상수로 설정하며 다음과 같이 찾는다.
$$\DeclareMathOperator*{\argminA}{arg\,min} F_0(x) = \argminA_{\gamma} \sum_{i=1}^nL(y_i, \gamma)$$
2. $m=1, \ldots, M$에 대하여 (a)~(d)를 반복한다.
(a) 다음과 같이 유사 잔차(Pseudo Residual)를 계산한다. $$r_{im} = -\left [ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right ]_{F(x)=F_{m-1}(x)} \;\; \text{for}\;\; i=1, \ldots, n$$
(b) 앞에서 구한 잔차를 새로운 종속변수로 하여 회귀 의사결정나무(Regression Tree) $g_m$을 학습한다. 즉, $(x_i, r_{im}), i=1, \ldots, n$을 이용하여 학습하게 된다. 이를 통해 $J_m$개 끝마디와, 영역 $R_{jm}, j=1, \ldots, J_m$을 얻게 된다.
(c) 상수 $\gamma_{jm}$을 다음과 같이 계산한다. $$\DeclareMathOperator*{\argminA}{arg\,min} \gamma_{jm} = \argminA_\gamma \sum_{x_i\in R_{jm}}L(y_i, F_{m-1}(x_i)+\gamma)$$
(d) 모형을 업데이트한다. $$F_m(x) = F_{m-1}(x)+l\sum_{j=1}^{J_m}\gamma_{jm}I(x\in R_{jm})$$
3. 최종 모형은 다음과 같다.
$$F_M(x)$$
2) 예제
여기서는 간단한 데이터를 통해 위 알고리즘이 어떻게 돌아가는지 회귀 문제, 분류 문제로 나누어 보려고 한다.
a. 회귀 문제
연간 독서량, 하루 컴퓨터 사용시간을 이용하여 수학 점수를 예측하는 문제가 있다고 하자. 데이터는 아래와 같다.

회귀 문제 하면 손실 함수는 자연스럽게 제곱손실함수를 떠오르기 마련이다.
$$L(y, F(x)) = \frac{1}{2}(y-F(x))^2$$
이제 Gradient Tree Boosting 알고리즘을 돌려보자.
1. 초기 모형은 상수로 설정하며 다음과 같이 찾는다.
$$\DeclareMathOperator*{\argminA}{arg\,min} F_0(x) = \argminA_{\gamma} \sum_{i=1}^nL(y_i, \gamma)$$
여기서 $\{y_i\}_{i=1}^5 $는 수학 성적이다. 이때에는 의사결정나무를 적합하는 것이 아니라 우리에게 익숙한 선형 회귀 모형을 상수로 적합시키는 경우이다. 이때 $\sum_{i=1}^5L(y_i, \gamma)$을 최소화하는 $\gamma$는 다음과 같다(계산은 미분값을 0으로 놓고 풀면 된다).
$$\gamma = \frac{1}{5} \sum_{i=1}^5y_i=78.8$$

2. $m=1, \ldots, M$에 대하여 (a)~(d)를 반복한다.
(a) 다음과 같이 유사 잔차(Pseudo Residual)를 계산한다. $$r_{im} = -\left [ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right ]_{F(x)=F_{m-1}(x)} \;\; \text{for}\;\; i=1, \ldots, n$$
여기서 $m=1$이다. 즉 첫 번째 스텝이라는 얘기다. 제곱 손실 함수 $L$에 대하여 유사 잔차는 다음과 같다.
$$r_{i1} = -\left [ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right ]_{F(x)=F_{0}(x)} = y_i-F_{0}(x)$$
왜 $r_{im}$이 유사 잔차라고 불리는지 알 수 있는 대목이다. 사실 여기에서 $r_{im}$는 유사 잔차가 아닌 회귀 분석에서 보았던 '진짜' 잔차이다. 왜 '유사'라는 말이 들어갔는지는 분류 문제에서 알 수 있다.

(b) 앞에서 구한 잔차를 새로운 종속변수로 하여 회귀 의사결정나무(Regression Tree) $g_m$을 학습한다. 즉, $(x_i, r_{im}), i=1, \ldots, n$을 이용하여 학습하게 된다. 이를 통해 $J_m$개 끝마디와, 영역 $R_{jm}, j=1, \ldots, J_m$을 얻게 된다.
예시를 위해 의사결정나무의 깊이는 1로 설정했고 $(x_i, r_{i1}), i=1, \ldots, 5$를 이용하여 의사결정나무를 학습한다. 이렇게 학습한 나무가 $g_1(x)$이 된다. $g_1(x)$의 끝마디 개수는 $J_1=2$이며
$$R_{11} = \{ x | \text{연 독서량} \leq 16\}, R_{21} = \{ x | \text{연 독서량} > 16\}$$
이다. 그리고 아래 그림과 같이 잔차들이 두 개 끝마디에 나뉘어 들어간다.

(c) 상수 $\gamma_{jm}$을 다음과 같이 계산한다. $$\DeclareMathOperator*{\argminA}{arg\,min} \gamma_{jm} = \argminA_\gamma \sum_{x_i\in R_{jm}}L(y_i, F_{m-1}(x_i)+\gamma)$$
$L$이 제곱 손실 함수이므로 다음과 같음을 알 수 있다.
$$\begin{align} \sum_{x_i\in R_{j1}}L(y_i, F_{0}(x_i)+\gamma) &= \frac{1}{2}\sum_{x_i\in R_{j1}}(y_i - F_{0}(x_i)-\gamma)^2 \\ &= \frac{1}{2}\sum_{x_i\in R_{j1}}(r_{i1}-\gamma)^2 \end{align}$$
따라서 $\gamma_{j1}, j=1, 2$는 각 끝마디에 속하는 잔차들의 평균임을 알 수 있다(계산은 미분값을 0으로 놓고 풀면 된다).
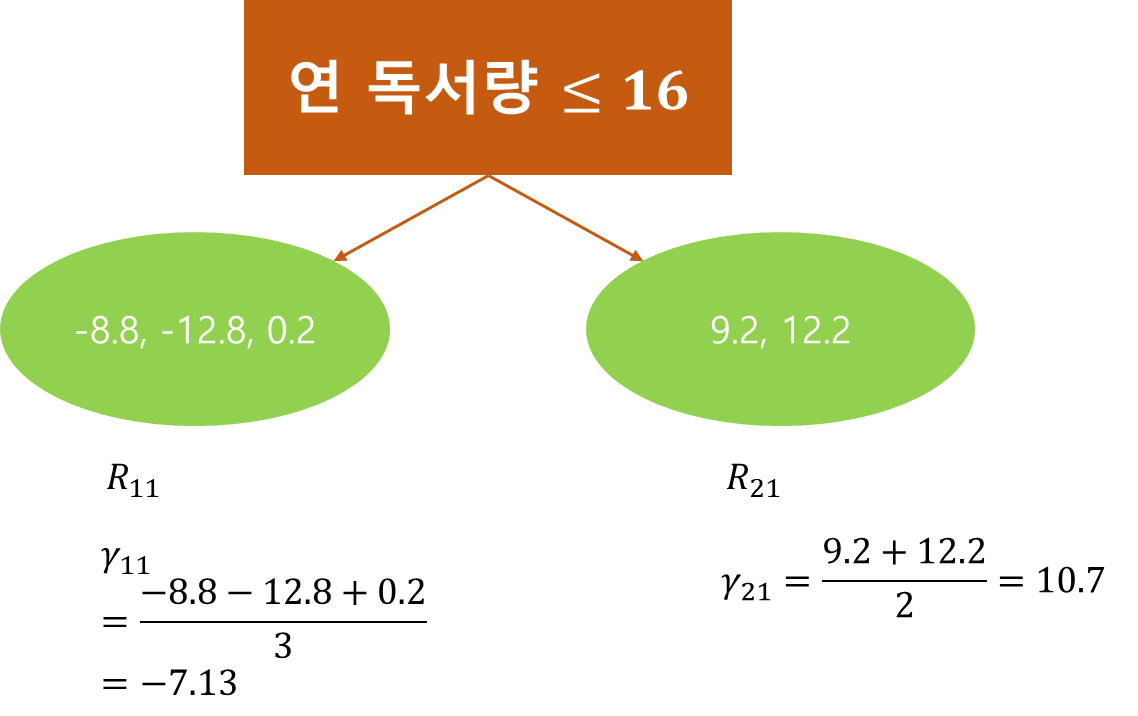
(d) 모형을 업데이트한다. $$F_m(x) = F_{m-1}(x)+l\sum_{j=1}^{J_m}\gamma_{jm}I(x\in R_{jm})$$
편의를 위해 $l=0.1$이라고 하자. 그렇다면 $F_1$은 다음과 같이 업데이트된다.
$$F_1(x) = F_{0}(x)+0.1\sum_{j=1}^{J_1}\gamma_{j1}I(x\in R_{j1}) = 78.8+0.1\sum_{j=1}^{2}\gamma_{j1}I(x\in R_{j1})$$
이제 이 과정을 미리 정해둔 반복수 $M$만큼 반복하게 된다.
3. 최종 모형은 다음과 같다.
$$F_M(x)$$
만약 $M=1$이고 연 독서량이 13, 하루 컴퓨터 사용시간이 2인 데이터에 대하여 수학 평균을 예측해보자.
해당 데이터는 연 독서량이 16보다 작거나 같으므로 영역 $R_{11}$에 속한다. 따라서 수학 평균을 예측하면 다음과 같다.
$$78.8+0.1\cdot \gamma_{11} = 78.8+0.1\cdot(-7.13) = 77.29$$
b. 분류 문제
이번엔 분류 문제에 Gradient Boosting Tree 알고리즘을 적용해보자. 여기에서는 2 분류 문제를 다룬다. 다중 클래스 분류는 One vs One, One vs All를 이용하여 풀 수 있다.
18. 다중 클래스(Multi-Class) 분류를 위한 One vs Rest, One vs One 방법을 알아보자.
연간 독서량, 하루 컴퓨터 사용시간을 이용하여 안경을 썼는지 여부를 예측한다고 해보자. 데이터는 다음과 같다. 안경 여부에서 1은 안경을 쓴다는 것이고 0은 안 쓴다는 것이다.

이제 알고리즘을 돌려보자.
1. 초기 모형은 상수로 설정하며 다음과 같이 찾는다.
$$\DeclareMathOperator*{\argminA}{arg\,min} F_0(x) = \argminA_{\gamma} \sum_{i=1}^nL(y_i, \gamma)$$
분류 문제에서는 손실 함수를 음의 로그 우도(Log Likelihood)를 사용한다.
$$L = -\sum_{i=1}^n[y_i\log(p_i)+(1-y_i)\log(1-p_i)]\tag{10}$$
여기서 $p_i$는 $P(y_i=1|x_i)$이다.
$\text{odd}_i = p_i/(1-p_i)$라 하자. 이를 이용하여 (10)을 변형하면 다음과 같다.
$$L = \sum_{i=1}^n[-y_i\log \text{odd}_i+\log (1+e^{\log \text{odd}_i})]$$
Gradient Tree Boosting은 로그 오즈를 이용하여 손실 함수를 다음과 같이 정의한다.
$$L(y_i, \gamma) = -y_i\gamma+\log(1+e^\gamma)$$
미분을 이용하면
$$F_0(x) = \argminA_{\gamma} \sum_{i=1}^nL(y_i, \gamma) = \log \left( \frac{\sum_{i=1}^ny_i}{n}/\left(1-\frac{\sum_{i=1}^ny_i}{n}\right) \right)$$
라는 것을 알 수 있다.
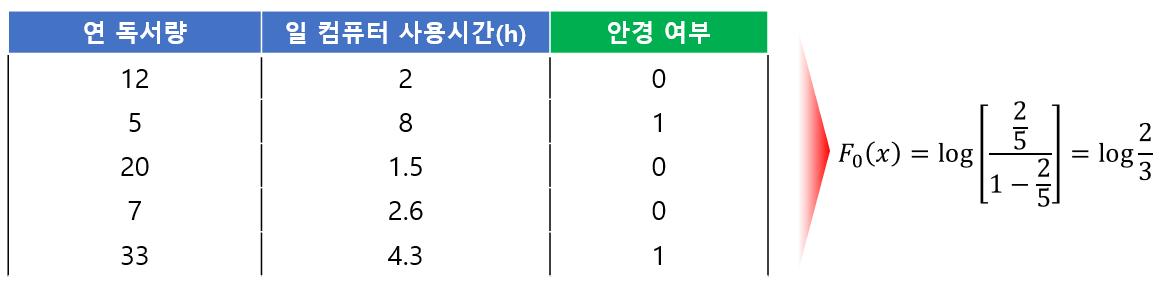
2. $m=1, \ldots, M$에 대하여 (a)~(d)를 반복한다.
(a) 다음과 같이 유사 잔차(Pseudo Residual)를 계산한다. $$r_{im} = -\left [ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right ]_{F(x)=F_{m-1}(x)} \;\; \text{for}\;\; i=1, \ldots, n$$
여기서 $m=1$이다. 이때 다음을 계산해야 한다.
$$\begin{align} -\left [ \frac{\partial L(y_i, F(x_i))}{\partial F(x_i)} \right ]_{F(x)=F_{0}(x)} &= \left [ \frac{\partial [y_iF(x_i)-\log (1+e^{F(x_i)})] }{\partial F(x_i)} \right ]_{F(x)=F_{0}(x)} \\ &= y_i-\frac{e^{F_0(x_i)}}{1+e^{F_0(x_i)}} \\ &= y_i- \hat{P}(y_i=1|x_i) \end{align}$$
위 결과를 통해 $r_{i1}$은 관측된 확률값에서 예측된 확률값을 뺀 값이 된다. 이는 관측치와 예측치를 뺀다는 관점에서 잔차와 유사한 역할을 한다고 할 수 있다. 이렇게 해서 $r_{im}$이 유사 잔차라고 불리게 된 것이다.

(b) 앞에서 구한 잔차를 새로운 종속변수로 하여 회귀 의사결정나무(Regression Tree) $g_m$을 학습한다. 즉, $(x_i, r_{im}), i=1, \ldots, n$을 이용하여 학습하게 된다. 이를 통해 $J_m$개 끝마디와, 영역 $R_{jm}, j=1, \ldots, J_m$을 얻게 된다.
이번에도 의사결정나무의 깊이는 1로 설정했고 $(x_i, r_{i1}), i=1, \ldots, 5$를 이용하여 의사결정나무를 학습한다. 이렇게 학습한 나무가 $g_1(x)$이 된다. $g_1(x)$의 끝마디 개수는 $J_1=2$이며
$$R_{11} = \{ x | \text{일 컴퓨터 사용시간} \leq 3.45\}, \\ R_{21} = \{ x | \text{일 컴퓨터 사용시간} > 3.45\}$$
이다.
그리고 아래 그림과 같이 잔차들이 두 개 끝마디에 나뉘어 들어간다.

(c) 상수 $\gamma_{jm}$을 다음과 같이 계산한다. $$\DeclareMathOperator*{\argminA}{arg\,min} \gamma_{jm} = \argminA_\gamma \sum_{x_i\in R_{jm}}L(y_i, F_{m-1}(x_i)+\gamma)$$
여기가 좀 복잡하다. 왜냐하면
$$\sum_{x_i\in R_{jm}}L(y_i, F_{m-1}(x_i)+\gamma)$$
을 $\gamma$에 대하여 미분하고 이를 0으로 놓고 풀어야 되는데 저 Summation($\sum$) 때문에 $\gamma$에 대하여 표현이 안된다. 따라서 여기서는 Talyor 2차 근사를 이용한다.
$$L(y_i, F_{m-1}(x_i)+\gamma)\\ \approx L(y_i, F_{m-1}(x_i)) +\frac{d}{d F}L(y_i, F_{m-1}(x_i))\gamma + \frac{1}{2}\frac{d^2}{dF^2}L(y_i, F_{m-1}(x_i))\gamma^2$$
양변을 $\gamma$에 대하여 미분하자.
$$\frac{d}{d\gamma}L(y_i, F_{m-1}(x_i)+\gamma) \\ \approx \frac{d}{d F}L(y_i, F_{m-1}(x_i)) + \frac{d^2}{dF^2}L(y_i, F_{m-1}(x_i))\gamma$$
이제 양변에 Summation을 취하고 $\gamma$에 대해서 정리해보자.
$$\gamma = \frac{-\sum_{x_i\in R_{jm}}\frac{d}{d F}L(y_i, F_{m-1}(x_i))}{\sum_{x_i\in R_{jm}}\frac{d^2}{dF^2}L(y_i, F_{m-1}(x_i))}$$
분모 분자는 다음과 같고
$$\begin{align} -\sum_{x_i\in R_{jm}}\frac{d}{d F}L(y_i, F_{m-1}(x_i)) &= \sum_{x_i\in R_{jm}}[y_i- \hat{P}(y_i=1|x_i)] \\ \sum_{x_i\in R_{jm}}\frac{d^2}{dF^2}L(y_i, F_{m-1}(x_i)) &= \sum_{x_i\in R_{jm}}[\hat{P}(y_i=1|x_i)(1-\hat{P}(y_i=1|x_i)) ]\end{align}$$
이를 종합하면
$$\gamma_{jm} = \frac{\sum_{x_i\in R_{jm}}[y_i- \hat{P}(y_i=1|x_i)]}{\sum_{x_i\in R_{jm}}[\hat{P}(y_i=1|x_i)(1-\hat{P}(y_i=1|x_i)) ]}$$
샘플 데이터에 대하여 위 식을 계산하면 다음 그림과 같다.

(d) 모형을 업데이트한다. $$F_m(x) = F_{m-1}(x)+l\sum_{j=1}^{J_m}\gamma_{jm}I(x\in R_{jm})$$
이는 회귀 문제에서와 동일하므로 패스~
3. 최종 모형은 다음과 같다.
$$F_M(x)$$
Gradient Tree Boosting을 분류 문제에 적용할 때 우리가 예측하는 것은 라벨 1에 대한 로그 오즈이다. 즉, 라벨을 예측하는 것이 아니라는 뜻이다.
따라서 새로운 데이터 $x$가 들어왔을 때 $F_M(x)>0$이면 $y=1$ 아닌 경우에는 $y=0$로 예측하게 된다.
4. 장단점 및 고려 사항
- 장점 -
a. 구현이 쉽다.
알고리즘 자체가 구현하기 어려운 것이 아니므로 기본 학습기(Base Learner)가 잘 구현되어 있다면 Gradient Boosting 알고리즘 구현은 쉬워진다.
b. 정확도가 좋다.
잔차를 계속해서 줄여나가는 방식으로 학습하기 때문에 정확도가 좋다.
c. 굉장히 유연하다.
여기서 유연하다는 것은 기본 학습기에 제한되지 않아 의사결정나무 이외에 다른 모형을 써도 된다는 것과 여러 가지 손실 함수를 적용할 수 있다는 뜻이다.
- 단점 -
a. 과적합이 발생할 가능성이 크다.
Gradient Boosting 자체가 잔차를 계속해서 줄여나가는 방식이라고 했다. 이는 장점이 될 수 있는 반면 Noise가 발생하는 경우 과적합이 발생할 수 있다.
b. 메모리 문제가 있다.
반복수 $M$만큼의 나무가 필요하므로 반복수가 커지면 나무도 많아져 많은 메모리를 사용해야 할 수 있다.
c. 해석이 어렵다.
각 입력 변수에 대하여 출력 변수가 어떻게 변하는지에 대한 해석이 어렵다.
- 고려 사항-
Gradient Boosting에서는 반복수 $M$과 축소 모수 $l$을 미리 지정해줘야한다. 이 값은 보통 교차 검증을 통하여 설정할 수 있다. 이때 두가지 값을 모두 교차 검증할 수 있지만 보통 $M$을 100정도로 설정하고 $l$만 교차 검증을 통해 선택한다.
5. 파이썬 구현
이제 Gradient Tree Boosting을 파이썬으로 구현해보려고 한다. 전체 노트북 파일은 아래 첨부해두었다.
먼저 Padnas와 Numpy를 임포트 해준다.
import pandas as pd
import numpy as np
그리고 지난 포스팅에서 다루었던 의사결정나무 코드가 있다. 여기에서는 Gradient Tree Boosting을 위해 조금 수정한 부분만 소개한다.
먼저 DecisionTree 클래스에서 createLeaf은 끝마디에서 출력 변수 y의 인덱스를 가져오게 했다. 그리고 예측을 수행하는 메서드 predict는 Gradient Tree Boosting 알고리즘에 맞게 수정해주었다. DecisionTree의 대한 구체적인 설명은 여기를 참고하기 바란다.
class DecisionTree:
'''중략'''
def createLeaf(self, y, tree_type):
return y.index
'''중략'''
def predict(self, X, gb_type='regression', pred_prob=None):
y = self.y
if gb_type=='regression':
pred = np.array([np.mean(y[self._traverse_tree(x, self.root)]) for _, x in X.iterrows()])
else:
pred = []
for _, x in X.iterrows():
numerator = np.sum(y[self._traverse_tree(x, self.root)])
target_prob = pred_prob[self._traverse_tree(x, self.root)]
denominator = np.sum(target_prob*(1-target_prob))
pred.append(numerator/denominator)
pred = np.array(pred)
return pred
이제 오늘의 주인공인 GradientTreeBoosting을 만나보자. 나는 초기 인자 gb_type로 분류(classification)와 회귀(regression)로 나누어 알고리즘을 적용시키게 했다.
class GradientTreeBoosting():
def __init__(self, gb_type='classification'):
assert gb_type in ['classification', 'regression']
self.gb_type = gb_type
self.trees = None ## 개별 트리 저장
self.constant = None ## 초기 예측값
self.predicted_prob = None ## 분류 문제인 경우 예측확률
self.learning_rate = None ## 학습률
return
다음으로 알고리즘을 수행하는 fit 메서드이다. 이 함수는 입력 변수 행렬 X, 출력 변수 y, 반복수 M, 학습률 learning_rate, 개별 트리의 최대 깊이 max_depth, 그리고 입력 변수 타입 type_of_col을 인자로 받는다. auto_determine_type_of_col는 신경 쓰지 않아도 된다. 처음에 gb_type에 따라서 초기값 $F_0(x)$를 계산한다. 그러고 나서 $M$번 반복마다 유사 잔차, 그리고 개별 트리 학습, 예측값 업데이트 순으로 알고리즘을 수행한다. 참고로 분류 문제의 경우 2 분류 문제만 다룰 수 있도록 했다. 다중 클래스까지 처리하려면 2 분류 GradientBoosting 클래스를 따로 만들어서 One vs One 또는 One vs All 방법을 적용해야 하는데 귀찮아서 만들지 않았다.
class GradientTreeBoosting():
'''중략'''
def fit(self, X, y, M=10, learning_rate=0.1, max_depth=3,
type_of_col=None, auto_determine_type_of_col=False):
self.learning_rate = learning_rate
## Initial F0
if self.gb_type == 'regression':
self.constant = np.mean(y)
pred_val = np.mean(y)
else:
n = len(y)
self.constant = np.log(np.sum(y)/n)
p_hat = np.sum(y)/n
cur_F = np.log(p_hat/(1-p_hat))
pred_val = p_hat
pred_val = pd.Series([pred_val]*len(y))
reg_tree = []
for m in range(M):
## pseudo residual
pseudo_residual = y-pred_val
## Fit Regression Tree
tree_model = DecisionTree(tree_type='regression')
tree_model.fit(X, pseudo_residual,
impurity_measure='mse',
min_sample=2,
max_depth=max_depth,
type_of_col=type_of_col,
auto_determine_type_of_col=auto_determine_type_of_col)
reg_tree.append(tree_model)
## get gamma and update predict value
if self.gb_type == 'regression':
pred_val += learning_rate*tree_model.predict(X, gb_type=self.gb_type)
else:
cur_F += learning_rate*tree_model.predict(X, gb_type=self.gb_type, pred_prob=pred_val)
pred_val = np.exp(cur_F)/(1+np.exp(cur_F))
self.trees = reg_tree
if self.gb_type == 'classification':
self.predicted_prob = pred_val
return
다음으로 예측을 수행하는 predict 메서드이다.
class GradientTreeBoosting():
'''중략'''
def predict(self, X):
l = self.learning_rate
trees = self.trees
pred = self.constant
for tree in trees:
if self.gb_type == 'regression':
pred += l*tree.predict(X, self.gb_type)
else:
pred += l*tree.predict(X, self.gb_type, self.predicted_prob)
if self.gb_type == 'classification':
pred = list(map(lambda x: 1 if x>0 else 0, pred))
pred = np.array(pred)
return pred
구현은 끝났다. 이제 실제 데이터를 이용해서 잘 구현되었는지 확인해보자.
6. 예제
여기서는 앞에서 구현한 GradientTreeBoosting을 실제 데이터에 적용하고 Scikit-learn에서 제공하는 것과 결과를 비교해보고자 한다.
1) 분류 문제
여기서는 붓꽃 데이터를 이용하여 분류를 해보고자 한다. 2 분류만 적용이 가능하므로 두 개의 라벨만을 고려했다.
from sklearn.datasets import load_iris
from sklearn.ensemble import GradientBoostingClassifier
iris = load_iris()
df = pd.DataFrame(iris.data, columns=iris.feature_names)
df['species'] = [iris.target_names[x] for x in iris.target]
df = df[df['species'].isin(['setosa', 'versicolor'])]
df['species'] = df['species'].map(lambda x: 1 if x == 'setosa' else 0)
df = df.reset_index(drop=True)
나는 반복수 20, 개별 트리 최대 깊이는 2, 학습률은 0.5로 설정하여 GradientTreeBoosting 알고리즘을 돌려보고 학습 데이터에 대한 정확도를 계산해보았다.
%%time
X = df[['petal length (cm)', 'petal width (cm)']]
y = df['species']
clf = GradientTreeBoosting()
clf.fit(X, y, M=20, max_depth=2,learning_rate=0.5, type_of_col=['continuous']*2)
print('정확도 : ', np.mean(y == clf.predict(X)))

정확도가 100% 였다. ㄷㄷ;;
이번엔 같은 조건으로 sklearn에서 제공하는 GradientBoostingClassifier를 사용해보았다.
%%time
sk_clf = GradientBoostingClassifier(n_estimators=20,learning_rate=0.5, max_depth=2).fit(X, y)
print('정확도 : ', np.mean(y == sk_clf.predict(X)))

정확도는 앞의 결과와 동일했다. 하지만 속도가 200배 가까이 차이 났다. ㄷㄷ;;
2) 회귀 문제
이번엔 회귀 문제에 적용시켜보자. 데이터는 보스턴 집값 데이터를 이용했다.
from sklearn.datasets import load_boston
from sklearn.ensemble import GradientBoostingRegressor
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['y'] = boston.target
X = df[['RM', 'LSTAT']]
y = df['y']
직접 구현한 GradientTreeBoosting을 적용해보고 잔차 제곱합을 계산했다. 세팅은 분류 문제에서와 동일하게 설정했다.
%%time
reg = GradientTreeBoosting(gb_type='regression')
reg.fit(X, y, M=20, max_depth=2,learning_rate=0.5, type_of_col=['continuous']*2)
print('잔차제곱합 : ', np.mean(np.square(y-reg.predict(X))))

잔차 제곱합은 10.31로 나왔다. 하지만 시간이 1분 가까이 걸렸다.
이번엔 sklearn에서 제공하는 GradientBoostingRegressor를 사용했다.
%%time
sk_reg = GradientBoostingRegressor(n_estimators=20,learning_rate=0.5, max_depth=2).fit(X, y)
print('잔차제곱합 : ', np.mean(np.square(y-sk_reg.predict(X))))

잔차제곱합은 동일하게 나왔다. 하지만 속도가 5000배 정도 빨랐다ㄷㄷ;; 오늘도 난 sklearn 개발자님들께 경의를 표하게 되었다.
이번 포스팅에서는 Gradient Boosting 알고리즘과 이를 변형한 Gradient Tree Boosting 알고리즘에 대해서 알아보고 파이썬으로 구현하는 방법까지 알아보았다. 구현하는 거 자체는 어렵지 않으나 속도를 생각하면 나처럼 고집부리지 말고 Scikit-Learn을 쓰면 된다.
이번 기회를 통해 Gradient Boosting에 대해 좀 더 정확하게 알게 되어 뿌듯하다.
참고자료
Gradient Boosting - Wiki
Yutube StatQuest - Gradient Boosting Part1~4
박창이, 김용대, 김진석, 송종우, 최호식 - R을 이용한 데이터마이닝

'통계 > 머신러닝' 카테고리의 다른 글
| 22. 로지스틱 회귀(Logistic Regression)에 대해서 알아보자. (364) | 2022.07.03 |
|---|---|
| 21. XGBoost에 대해서 알아보자 (402) | 2022.06.26 |
| 19. 서포트 벡터 머신(Support Vector Machine)에 대해서 알아보자 with Python (414) | 2022.05.16 |
| 18. 다중 클래스(Multi-Class) 분류를 위한 One vs Rest, One vs One 방법을 알아보자. (397) | 2022.05.09 |
| 17. Dunn Index와 실루엣(Silhouette) 계수를 이용하여 최적 클러스터(군집, Cluster)개수 정하기 with Python (388) | 2022.05.07 |





댓글