이번 포스팅에서는 로지스틱 회귀에 대한 개념과 적합 알고리즘에 대해서 소개한다.
- 목차 -
1. 로지스틱 회귀(Logistic Regression)란 무엇인가?
본 포스팅에서는 수식을 포함하고 있습니다.
티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니
PC 웹 브라우저 또는 모바일 웹 브라우저에서 보시기 바랍니다.
1. 로지스틱 회귀(Logistic Regression)란 무엇인가?
로지스틱 회귀는 분류 문제에서 활용되는 회귀 모형이며 그 정의는 다음과 같다.
로지스틱 회귀는 출력 변수의 조건부 확률을 Softmax 함수를 이용하여 모델링한 것이다.
이 말의 뜻을 살펴보자.
a. Softmax 함수란 무엇인가?
Softmax 함수는 $K$범주 분류 문제에 있어서 각 범주의 예측 확률을 추정할 때 많이 활용되는 함수로 다음과 같이 정의된다.
$$\sigma (z)_i = \frac{e^{z_i}}{\sum_{j=1}^Ke^{z_j}}, \;\;\text{for} \; i=1, \ldots, K, \; z=(z_1, \ldots, z_K)$$
b. 로지스틱 회귀는 출력 변수의 조건부 확률을 Softmax를 이용하여 모델링한 것이다.
먼저 데이터 $(x_i, y_i), i=1, \ldots, n$이 있다. 이때 $x_i=(x_{i1}, \ldots, x_{ip})^t, y_i\in \{1, \ldots, K\}$이다.
로지스틱 회귀는 개별 관측치에 대한 조건부 확률을 다음과 같이 모델링한다.
$$\begin{align}P(y_i=j|x_i) &= \frac{e^{b_{0j} + b_{1j}x_{i1}+\cdots+b_{pj}x_{ip}}} {1+\sum_{k=1}^{K-1}e^{b_{0k} + b_{1k}x_{i1}+\cdots+b_{pk}x_{ip}}} , i=1, \ldots, n, j=1, \ldots, K-1, \\ P(y_i=K|x_i) &= \frac{1} {1+\sum_{k=1}^{K-1}e^{b_{0k} + b_{1k}x_{i1}+\cdots+b_{pk}x_{ip}}} \end{align}$$
실제로 추정하는 것은 $K-1$개의 조건부 확률이며 나머지 하나는 확률의 합이 1이라는 것을 이용하면 자동적으로 구할 수 있는 것이다.
근데 왜 하필 Softmax를 이용하여 모델링하는 것일까?
로지스틱 회귀는 $y$가 범주형인 경우에 사용하는 회귀 모형이다. 예를 들어 $y_i\in \{0, 1\}$인 경우 로지스틱 회귀 모형은 주어진 $x$에 대하여 $y=0$ 또는 $y=1$로 예측해야 한다. 이를 예측하기 위해선 먼저 $P(y=1|x)$를 먼저 추정하고 이 값이 0.5보다 크면 $y=1$ 아니면 $y=0$으로 예측하게 된다. 다시 말해 우리는 $x$가 주어졌을 대 $y=1$인 조건부 확률을 추정해야 하는 것이다. 그렇다면 다음과 같은 질문을 할 수 있다.
그럼 조건부 확률 $P(y=1|x)$을 선형으로 모델링하면 안 되나요?
-> 안된다.
왜냐하면 선형 모형의 Range가 $(-\infty, \infty)$인 반면 확률은 Range가 $[0, 1]$이기 때문이다. 아래 그림과 같이 $y\in \{0,1 \}$인 데이터가 있는 상황에서 초록 직선과 같이 모델링하면 어느 순간부터는 0과 1을 벗어나기 때문에 직선은 확률을 추정하는 데 있어 적합하지 않다.
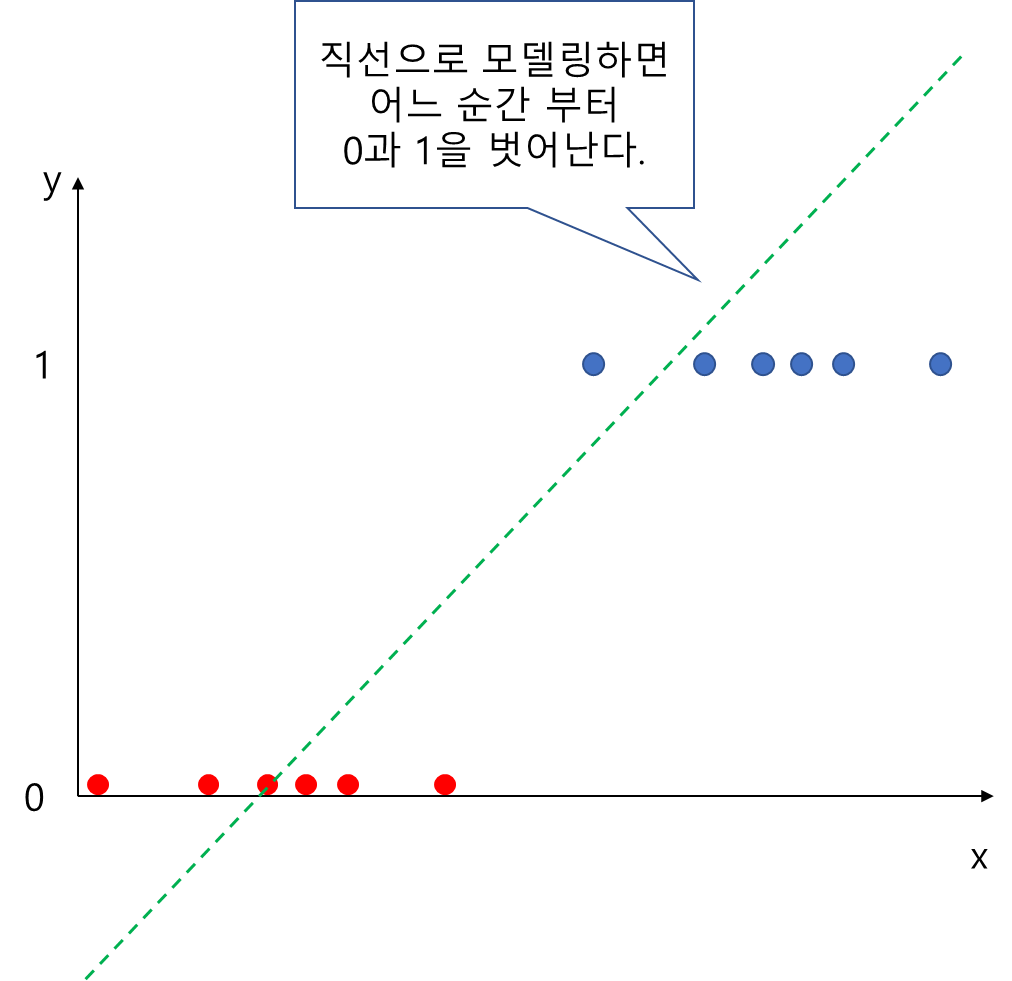
물론 어느 혹자는 다음과 같은 모형을 제안할 수 있다.
$$P(y=1|x) = \begin{cases} 1 &\text{if} \; b_0+b_1x_1+\cdots+b_px_p \geq 1 \\ 0 &\text{if}\; b_0+b_1x_1+\cdots+b_px_p \leq 0 \\ b_0+b_1x_1+\cdots+b_px_p &\text{o.w} \end{cases}$$
하지만 이 경우 $b_j, j=1, \ldots, p$에 대한 해석이 문제가 된다.
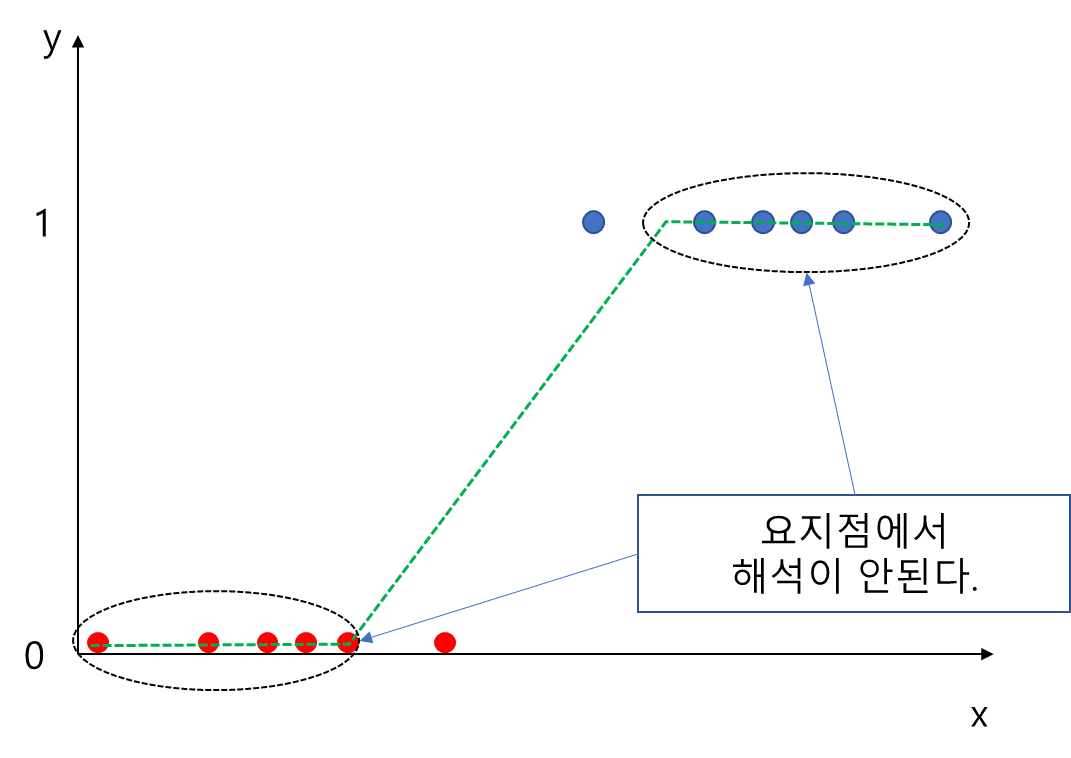
이러한 문제(Range, 해석)를 해결하기 위하여 Softmax를 도입하게 된다. Softmax는 Range가 $(0, 1)$이기 때문에 확률값의 범위와 일치하며 해석에 대한 일관성을 유지할 수 있다. 이러한 이유로 Softmax를 이용하여 모델링하게 된 것이다.
c. 회귀 계수의 해석?
편의상 이 분류 문제($y\in \{0,1\}$)를 다룬다고 해보자. 설명 변수가 하나 있다고 해보자. 그렇다면 로지스틱 회귀 모형은 다음과 같을 것이다.
$$P(y=1|x) = \frac{e^{b_0+b_1x}}{1+e^{b_0+b_1x}}$$
이때 $p = P(y=1|x)$라 하면 다음과 같다.
$$\log \frac{p}{1-p} = b_0+b_1x$$
이를 이용하여 $b_1$을 정리하면 다음과 같다.
$$\begin{align}b_1 &= b_0 + b_1(x+1) - [b_0+b_1x] \\ &= \log \frac{P(y=1|x+1)}{1-P(y=1|x+1)} - \log \frac{P(y=1|x)}{1-P(y=1|x)} \\ &= \log \frac{ \frac{P(y=1|x+1)}{1-P(y=1|x+1)} }{\frac{P(y=1|x)}{1-P(y=1|x)}} \end{align}$$
위 식을 통해 알 수 있는 것은 $b_1$은 설명 변수 $x$인 경우에 대한 설명 변수 $x+1$의 로그 오즈비라는 것이다.
하지만 로그 오즈비라는 해석은 이 분류(Binary Class) 문제에 대해서만 가능하고 다중 클래스(Multi Class) 문제에서는 그렇게 해석이 안된다.
$K$ 범주를 갖는 분류 문제에서 회귀 계수의 해석을 생각해보자. $y\in \{1, 2, \ldots, K\}$이다. 편의상 설명 변수는 한 개 있다고 해보자. 그렇다면 로지스틱 회귀(Logistic Regression)는 각 범주에 대한 조건부 확률을 다음과 같이 추정하게 된다.
$$\begin{align} P(Y=j | x) &= \frac{e^{b_{0j}+b_{1j}x}}{1+\sum_{k=1}^{K-1}e^{b_{0k}+b_{1k}x}}, j=1,\ldots, K-1 \\ P(Y=K|x) &= \frac{1}{1+\sum_{k=1}^{K-1}e^{b_{0k}+b_{1k}x}} \end{align}$$
이를 잘 정리하면 다음과 같다.
$$\log \frac{P(y=j|x)}{P(y=K|x)} = b_{0j}+b_{1j}x \tag{1}$$
이제 앞에서와 같이 정리하면 다음과 같다.
$$\begin{align}b_{1j} &= b_{0j} + b_{1j}(x+1) - [b_{0j}+b_{1j}x] \\ &= \log \frac{P(y=j|x+1)}{P(y=K|x+1)} - \log \frac{P(y=j|x)}{P(y=K|x)} \\ &= \log \frac{ \frac{P(y=j|x+1)}{P(y=K|x+1)} }{\frac{P(y=j|x)}{P(y=K|x)}} \end{align} \tag{2}$$
(2)를 통해 알 수 있는 것은 회귀 계수가 이 분류에서와 같이 로그 오즈비로 해석이 안된다는 것이다. 굳이 해석하자면 $x$가 한 단위 증가할 때 $K$ 범주에 대한 $j$의 조건부 확률 비의 로그 변화율 정도로 해석할 수 있겠다.
2. 로지스틱 회귀 적합 알고리즘
로지스틱 회귀 모형의 적합은 최대 우도 추정을 이용한다. 그렇다면 먼저 로그 우도 함수를 계산해보자. 먼저 데이터가 $(x_i, y_i), i=1, \ldots, n$이 있다. 이때 $x_i=(1, x_{1i}, x_{2i}, \ldots, x_{pi})$는 $p+1$차원 입력 변수 벡터이고 $y_i = (y_{i1}, \ldots, y_{iK})$으로 $y$가 $j$범주라면 $y_{ij}=1$이고 $y_{ih} = 0 , \text{for}\; h \neq j$이다.
이제 로그 우도 함수를 계산해보자.
$$\begin{align}L(b) &= \log \prod_{i=1}^n\prod_{j=1}^Kp_{ij}^{y_{ij}} \\ &=\sum_{i=1}^n \left \{ \sum_{j=1}^{K-1}y_{ij}x_i^tb_j -\log \left [ 1+\sum_{j=1}^{K-1}e^{x_i^tb_j} \right ] \right \} \\&= \sum_{j=1}^{K-1}\left [ \sum_{k=1}^pb_{jk} \left ( \sum_{i=1}^n x_{ik}y_{ij} \right ) \right ] - \sum_{i=1}^n\log \left [ 1 + \sum_{j=1}^{K-1}e^{x_i^tb_j} \right ] \end{align}$$
여기서 $$\begin{align}b_j &= (b_{0j}, b_{1j}, \ldots, b_{pj})^t, \\ p_{ij} &= \frac{e^{x_i^tb_j}}{1+\sum_{k=1}^{K-1}e^{x_i^tb_j}}, j=1, \ldots, K-1, \tag{3}\\ p_{iK} &= \frac{1}{1+\sum_{k=1}^{K-1}e^{x_i^tb_j}}\tag{4} \end{align}$$
이다.
이제 로그 우도 함수 $L$의 1차 미분과 2차 미분을 구해야 한다.
$$\frac{\partial L(b)}{\partial b_{jk}} = \sum_{i=1}^nx_{ik}(y_{ij}-p_{ij}), \;\; j=1, \ldots, K-1, k=0, \ldots, p \tag{5}$$ $$\frac{\partial^2 L(b)}{\partial b_j \partial b_{j'}} = -\sum_{i=1}^np_{ij}[I(j=j')-p_{ij'}]x_i^tx_i\;\; j, j' = 1, \ldots, K-1 \tag{6}$$
이를 이용한 로지스틱 회귀 모형 적합 알고리즘은 다음과 같다.
Algorithm
1. 오차 범위 $\epsilon$, 최대 반복수 $T$ 그리고 $(K-1)\times(p+1)$ 벡터 $b^{(0)}$의 초기값을 설정한다.
2. $b^{(t)}$에 대하여 $b^{(t+1)}$를 다음과 같이 업데이트한다.
$$ b^{(t+1)} = b^{(t)} - \left ( \frac{\partial^2 L(b)}{\partial b \partial b^t} \right )^{-1} \left [\frac{\partial L(b)}{\partial b}\right ]_{b = b^{(t)}} $$
여기서 $\frac{\partial^2 L(b)}{\partial b \partial b^t}$는 $j$행, $j'$열의 행렬이 (6)과 같이 주어지는 Block 행렬이며
$$\frac{\partial L(b)}{\partial b} = \left (\frac{\partial L(b)}{\partial b_1}^t, \ldots, \frac{\partial L(b)}{\partial b_{K-1}}^t \right )$$
이다. 이때 $j$번째 벡터에 $k$번째 원소 $\frac{\partial L(b)}{\partial b_{jk}}$는 (5)와 같이 주어진다.
3. 최대 반복수 $T$에 도달했거나 $\|b^{(t+1)} - b^{(t)} \| < \epsilon$이면 알고리즘을 종료하고 $b^{(t+1)}$을 최종 회귀 추정량으로 설정한다. 만약 아니라면 2단계로 돌아간다.
알고리즘을 이용하여 회귀 계수 추정량을 얻었으면 예측은 다음과 같이 수행한다.
$$\DeclareMathOperator*{\argmaxA}{arg\,max} \hat{y} = \argmaxA_{j}P(y=j|x) $$
이때
$$\begin{align}P(y=j|x) &= \frac{e^{b_{0j} + b_{1j}x_{1}+\cdots+b_{pj}x_{p}}} {1+\sum_{k=1}^{K-1}e^{b_{0k} + b_{1k}x_{1}+\cdots+b_{pk}x_{p}}} , j=1, \ldots, K-1, \\ P(y=K|x) &= \frac{1} {1+\sum_{k=1}^{K-1}e^{b_{0k} + b_{1k}x_{1}+\cdots+b_{pk}x_{p}}} \end{align}$$
이다.
3. 장단점
- 장점 -
a. 회귀 계수의 해석이 가능하다.
앞에서 살펴보았듯이 로지스틱에서 회귀 계수는 $x$가 한 단위 증가할 때 특정 범주의 조건부 확률의 로그 변화율로 해석할 수 있다.
b. 클래스에 속할 확률을 추정한다.
대부분의 분류 모형의 경우(예: 랜덤포레스트, 의사결정나무, 부스팅, 서포트 벡터 머신 등) 특정 클래스를 예측하지만 로지스틱 회귀는 클래스에 속할 확률을 계산해준다. 따라서 확률 자체에 관심이 있는 분야(예: 위험도 분석(Risk Analysis))에서는 로지스틱 회귀가 자주 활용된다.
c. 저차원에서 과적합 가능성이 적다고 한다.
저차원 자료에서 데이터 샘플 수가 충분하면 과적합이 덜 일어난다고 한다.
d. 분류 문제에서 베이스 모형으로 활용 가능하다.
특정 분류 모형의 성능을 비교 평가하고 싶을 때 비교 모형(베이스 모형)으로 로지스틱 회귀를 생각해볼 수 있다.
- 단점 -
a. 분류 경계가 선형이다.
설명 변수가 하나인 이 분류 로지스틱 회귀에서 $P(y=1|x)>c$이면 클래스 1로 분류하는 규칙을 생각해보자. 이는
$$ b_0 + b_1x = \log \frac{P(y=1|x)}{1-P(y=1|x)} > \log \frac{1+c}{c}$$
의 경우 클래스 1로 분류하는 것과 같다. 따라서 분류 경계는 선형이며 비선형 경계를 갖는 복잡한 패턴을 학습할 수 없다.
b. 이상치에 민감하다.
로지스틱 회귀 모형은 이상치에 민감하다고 한다.
원래 파이썬 구현까지 하려고 했으나 코드가 잘못된 탓인지 추정량이 수렴을 안 했다. 다시 살펴보고 나중에 기회가 되면 구현한 것도 추가해보겠다.

'통계 > 머신러닝' 카테고리의 다른 글
| 24. 랜덤 포레스트(Random Forest)에 대해서 알아보자 (3) | 2022.08.05 |
|---|---|
| 23. 배깅(Bagging)에 대해서 알아보자 (0) | 2022.07.20 |
| 21. XGBoost에 대해서 알아보자 (402) | 2022.06.26 |
| 20. Gradient Boosting 알고리즘에 대해서 알아보자 with Python (408) | 2022.06.13 |
| 19. 서포트 벡터 머신(Support Vector Machine)에 대해서 알아보자 with Python (414) | 2022.05.16 |





댓글