클러스터링 문제에서는 최적 클러스터(군집, Cluster) 개수를 정하는 것이 문제가 된다. 이번 포스팅에서는 Dunn Index와 실루엣(Silhouette) 계수를 이용하여 클러스터(군집, Cluster) 개수를 정하는 방법에 대해서 알아본다.
- 목차 -
이번 포스팅을 읽기에 앞서 Dunn Index와 실루엣(Silhouette) 계수에 대해서 생소하다면 아래 포스팅에 설명해 두었으니 참고하기 바란다.
12. 클러스터링(군집화) 평가 지표 Dunn Index with Python
12. 클러스터링(군집화) 평가 지표 Dunn Index with Python
이번 포스팅에서는 클러스터링(군집화)이 잘되었는지 정량적으로 확인할 수 있는 평가 지표로 Dunn Index를 소개하려고 한다. 또한 Dunn Index를 파이썬(Python)으로 구현해보고자 한다. 1. 클러스터링(
zephyrus1111.tistory.com
14. 클러스터링(군집화) 평가지표 Silhouette(실루엣) 지수(계수)에 대해서 알아보자 with Python
14. 클러스터링(군집화) 평가지표 Silhouette(실루엣) 지수(계수)에 대해서 알아보자 with Python
이번 포스팅에서는 클러스터링(군집화)이 잘되었는지 정량적으로 확인할 수 있는 Silhouette(실루엣) 지수(계수)에 대해서 알아보고 파이썬(Python)으로 구현하는 방법에 대해서 알아보려고 한다. 또
zephyrus1111.tistory.com
이 곳은 꽁냥이가 머신러닝을 공부한 내용을 정리하는 곳입니다.
이 포스팅에서는 수식을 포함하고 있습니다. 티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니 웹브라우저 또는 모바일 웹브라우저로 보시길 바랍니다.
1. 데이터 준비
먼저 이번 포스팅에서 사용할 모듈을 임포트하고 데이터를 만들어준다. 이때 아래 파이썬 파일이 필요하다. 이는 Dunn Index를 계산하는 함수를 포함하고 있다.
import numpy as np
import matplotlib.pyplot as plt
from cluster_eval import get_Dunn_index
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
np.random.seed(100)
num_data = 50
x11 = np.linspace(0.3,0.7,20)
label1 = [0]*len(x11)
x12 = np.linspace(1.3,1.8,15)
label2 = [1]*len(x12)
x13 = np.linspace(2.4,3,15)
label3 = [2]*len(x13)
x1 = np.concatenate((x11,x12,x13),axis=None)
error = np.random.normal(1,0.5,num_data)
x2 = 1.5*x1+2+error
X = np.stack((x1, x2), axis=1)
labels = np.array(label1+label2+label3)
데이터가 어떻게 생겼는지 시각화해보자~~!!
fig = plt.figure(figsize=(7,7))
fig.set_facecolor('white')
for i, x in enumerate(X):
plt.scatter(x[0], x[1], color='k')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
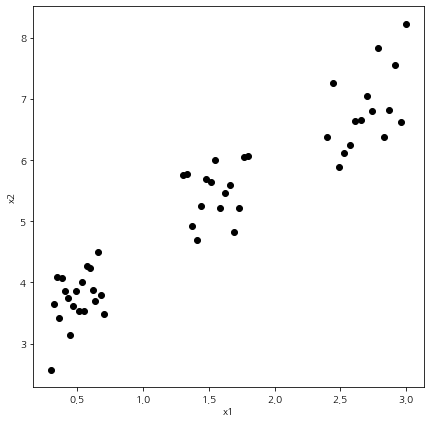
딱 보아도 최적 클러스터는 3개이다.
2. 최적 클러스터 개수 선정하기
이제 Dunn Index와 실루엣(Silhouette) 계수를 이용하여 최적 군집을 결정해보자. 두 지표 모두 값이 클수록 클러스터링(군집화)이 잘되었다는 뜻이며 이 값이 높은 클러스터 개수를 최적 개수로 정한다.
이때 클러스터 개수는 2개부터 10개까지 지정했고 클러스터링 알고리즘은 K-Means를 사용했다.
cluster_num_candidates = range(2,11)
Dunn_index_list = []
silhouette_list = []
for k in cluster_num_candidates:
kmeans = KMeans(n_clusters=k, random_state=100).fit(X)
kmeans_labels = kmeans.labels_
Dunn_index = get_Dunn_index(X, kmeans_labels)
ss = silhouette_score(X, kmeans_labels, metric='euclidean')
Dunn_index_list.append(Dunn_index)
silhouette_list.append(ss)
이제 결과를 눈으로 확인해보자.
fig = plt.figure(figsize=(9,6))
fig.set_facecolor('white')
plt.plot(cluster_num_candidates, silhouette_list, marker='o', label='Silhouette Index')
plt.plot(cluster_num_candidates, Dunn_index_list, marker='o', label='Dunn Index')
plt.legend()
plt.xlabel('The Number of Cluster')
plt.ylabel('Value')
plt.show()

Dunn Index는 클러스터(군집) 개수가 2일 때 최대값을 가졌고 실루엣(Silhouette) 계수는 3일 때 최대였다.
즉, Dunn Index 상으로는 최적 클러스터(군집) 개수가 2개이고 실루엣(Silhouette) 계수는 최적 클러스터(군집) 개수를 3으로 선택한다는 것이다.
일반화할 수 없겠지만 이번 결과만 놓고 보면 Dunn Index 보다 실루엣(Silhouette) 계수가 더 정확한 클러스터 개수를 선택하였다.
이번 포스팅에서는 최적 클러스터(군집) 개수를 찾아보는 방법에 대해서 알아보았다. 실험에서는 클러스터링 알고리즘으로 K-Means를 사용했지만 가우시안 혼합 모형(Gaussian Mixture Model) 클러스터링을 써도 좋다.
다음에는 비모수 베이지안 방법으로 자동적으로 최적 클러스터(군집) 개수를 찾아내는 방법을 알아보려고 한다.

'통계 > 머신러닝' 카테고리의 다른 글
| 19. 서포트 벡터 머신(Support Vector Machine)에 대해서 알아보자 with Python (414) | 2022.05.16 |
|---|---|
| 18. 다중 클래스(Multi-Class) 분류를 위한 One vs Rest, One vs One 방법을 알아보자. (397) | 2022.05.09 |
| 16. 선형 회귀(Linear Regression) 모형에 대해서 알아보자 with Python (416) | 2022.05.06 |
| 15. AdaBoost(Adaptive Boost) 알고리즘에 대해서 알아보자 with Python (382) | 2022.05.06 |
| 14. 클러스터링(군집화) 평가지표 Silhouette(실루엣) 지수(계수)에 대해서 알아보자 with Python (410) | 2022.05.01 |





댓글