이번 포스팅에서는 게임 이론에서 상금 분배 방법의 하나인 Shapley Value와 이를 머신러닝 예측 모형을 해석하는 데 활용한 SHAP에 대해서 알아보고자 한다. 그리고 SHAP Value를 계산하는 과정을 파이썬(Python)으로 구현해보고자 한다.
- 목차 -
1. Shapley Value란?
1) 배경
Shapley Value(SV)는 공정 분배 게임 이론에서 나온 개념으로 주어진 게임에 참여한 플레이어들에게 상금을 공정하게 배분하는 하나의 방법을 말한다.
SV에 대한 수학적 정의를 내리기 위해 기본적인 정의를 해보자. 먼저 주어진 게임에 참여한 총플레이어가 $n$명이라 하고 각 플레이어는 1번부터 $n$번까지 번호가 부여되어있다. 이를 집합으로 표현하면 다음과 같다.
$$N = \{1, 2, \ldots, n \}$$
이제 협력체(Coalition) $S$는 $N$의 부분집합이다. 총 $n$명의 플레이어가 게임에 다 참여하는 경우는 $S=N$이며 게임에 아무도 참여하지 않는 경우는 $S=\emptyset$이다. 즉, 협력체 $S$는 $n$명의 플레이어 중에서 일부만 게임에 참가하는 경우를 나타내는 일반적인 의미인 것이다.
그리고 협력체 $S$에 대하여 이 협력체가 얼마만큼의 상금을 만들어내는지 알려주는 가치함수 $v$를 정의한다. 즉, $v$는 다음과 같이 $N$의 모든 부분 집합을 모아놓은 집합 $\mathcal{P}(N)$(이를 $N$의 Power Set이라 한다)상에서 정의된 실수 값을 갖는 함수이다.
$$v : \mathcal{P}(N) \longrightarrow \mathbb{R}$$
이다.
가치 함수는 기본적으로 다음을 가정한다.
$$v(\emptyset) = 0$$
당연한 것이다.!! 아무도 참여하지 않으면 그 게임에서 얻을 수 있는 총상금은 0이 되어야 합리적이기 때문이다.
또한 가치 함수는 선형성을 가정한다.
$$(v+w)(S) = v(S)+w(S), \;\; \forall S\subset N$$
즉, 모든 협력체 $S$에 대한 가치 합의 함수는 각 가치 함수의 합을 더한 것과 같다고 가정하는 것이다. 자연스럽다. 왜냐하면 아래와 같이 어떤 협력체 $S$에 대하여
$$(v+w)(S) \neq v(S)+w(S)$$
이어야할 이유가 없기 때문이다.
이제 분배 과정 $\phi$를 정의할 수 있다. $\phi$는 가치 함수 $v$와 플레이어 총집합 $N$이 주어졌을 때 $n$명의 플레이어에게 상금을 분배하는 매핑이다. 즉,
$$\phi (v, N) = (\phi_1(v, N), \ldots, \phi_n(v, N)) \in \mathbb{R}^n \tag{1}$$
이라고 할 수 있다.
하지만 이러한 분배 과정은 정의하기에 따라서 무수히 많을 것이다. 따라서 어떤 성질을 정의하여 그 성질을 만족하는 분배 과정을 조사하는 것이 바람직할 것이다. 근데 아무 성질을 정의하면 안 되고 상식적으로 분배 과정이 공정하다는 것을 인간이 느낄 수 있는 성질이어야 할 것이다.
이때 상식적으로 공정한 분배 과정이 무엇인지를 생각해보자.
(1) 효율성(Efficiency)
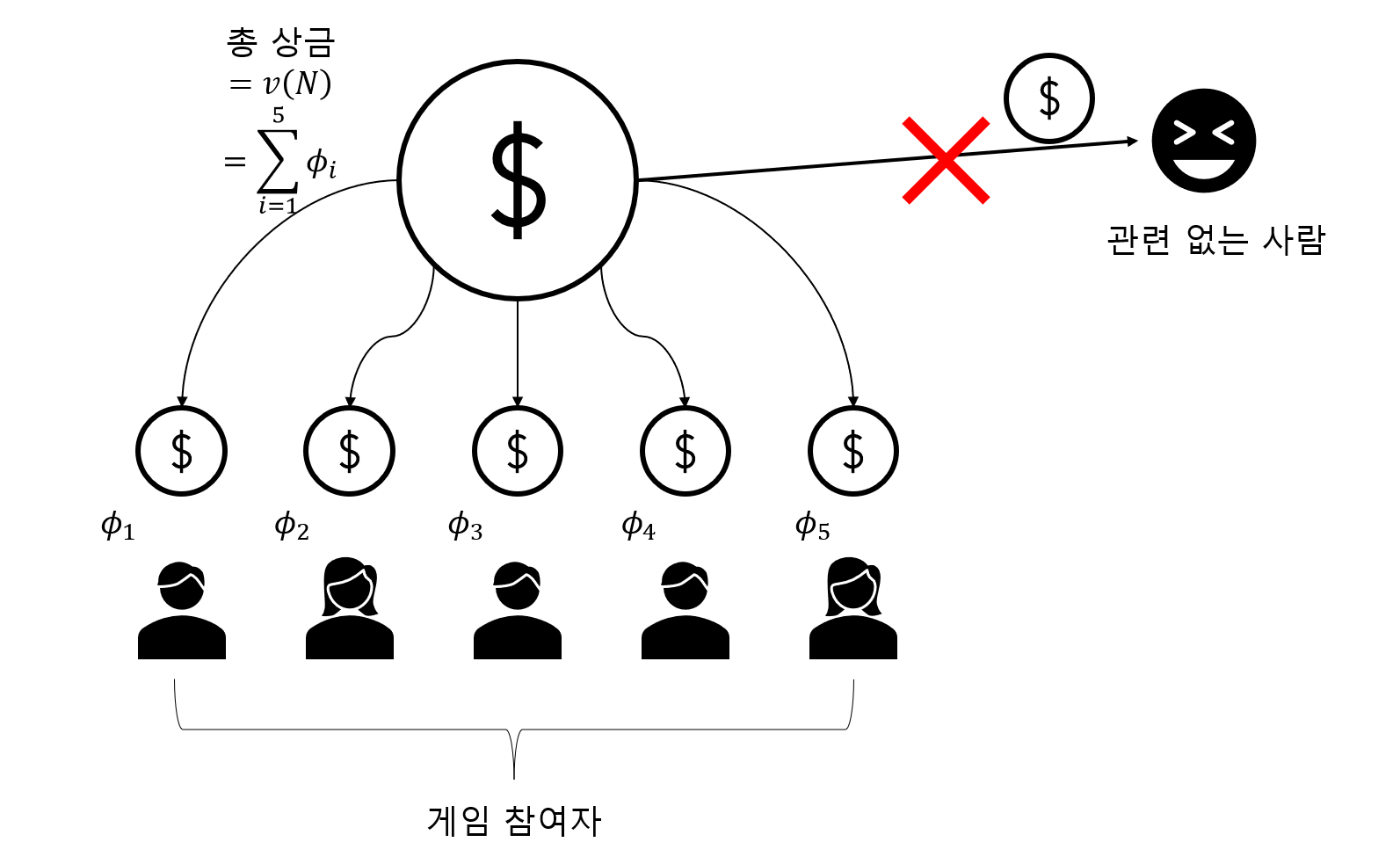
모든 플레이어가 게임에 참여한 경우에 받을 수 있는 총상금은 $v(N)$으로 표현할 수 있다. 그렇다면 분배 과정 $\phi$가 주어진 경우 각 플레이어에게 주는 상금의 합은 총 상금 $v(N)$과 같아야 공정할 것이다. 즉,
$$\sum_{i=1}^n\phi_i(v, N) = v(N) \tag{2}$$
이제부터는 $\phi_i = \phi_i(v, N)$이라 하겠다.
(2)를 다시 말하면 총상금이 해당 게임에 참여한 플레이어에게 남김없이 나눠줘야 한다는 것이다. 중간에 아무 상관없는 사람이 슬쩍하면 안 된다는 것이다. 이게 바로 공정한 분배 과정이 갖추어야 할 하나의 바람직한 성질인 것이다. 이러한 성질을 상금을 효율적으로 쓴다는 의미에서 분배 과정의 효율성이라 한다. 아래 그림은 효율성의 개념을 나타낸 것이다.
(2) 위장 플레이어(Dummy Player)
팀 플레이어에서 아무짝에도 쓸모없는 사람한테는 상금을 주지 않는 것이 공정하다고 할 수 있다(무임승차 방지). 여기서 질문이 나올 수 있다.
무임 승차 방지는 알겠는데
플레이어가 쓸모가 있는지 없는지 어떻게 판단하는가?
여기에서 각 플레이어의 기여도라는 개념이 필요하다(아직까지 기여도라는 개념이 없었음을 알아야 한다). 플레이어의 기여도는 해당 플레이어가 있고 없고에 따라서 생산해낼 수 있는 가치가 많이 달라지느냐 아니냐로 정의할 수 있다.
이때 $v$가 가치를 측정하는 함수이므로 이를 이용하여 플레이어 $i$의 가치 $v^i$를 정의할 수 있다.
$$v^i(S) =v(S\cup \{i\})-v(S) \;\;\text{for} \;\; S \subset N-\{i\} \tag{3}$$
이제 가짜 플레이어에 대한 정의를 할 수 있다.
$$v^i(S) =v(S\cup \{i\})-v(S)=0 \;\;\text{for all} \;\; S \subset N-\{i\} \\ \Rightarrow \phi_i=0 \tag{4}$$
즉, 기여도가 0인 플레이어(위장 플레이어)에게 줄 상금은 없다는 것이다(아래 그림 참고).

(3) 대칭성(Symmetry)
두 플레이어가 만들어내는 가치가 같다면 또는 두 플레이어의 기여도가 같다면 두 플레이어가 가져야 할 상금도 같아야 공정할 것이다. 아래 그림은 이러한 원리를 나타낸 것이다.

이를 수식으로 표현하면 다음과 같다.
$$ v^i(S) = v^j(S) \;\;\text{for all } \;\; S\subset N-\{i, j\} \Rightarrow \phi_i = \phi_j \tag{5}$$
위 성질을 만족하는 분배 과정 $\phi$를 대칭성(Symmetry)이 있다고 한다.
(4) 강한 단조성(Strong Monotonicity)
어떤 플레이어가 게임을 기존과는 다른 방식으로 하여 더 많은 가치(더 큰 기여)를 했다고 하자. 그렇다면 이 사람은 더 많은 상금을 받아야 할 것이다. 그래야 공정인 것이다.
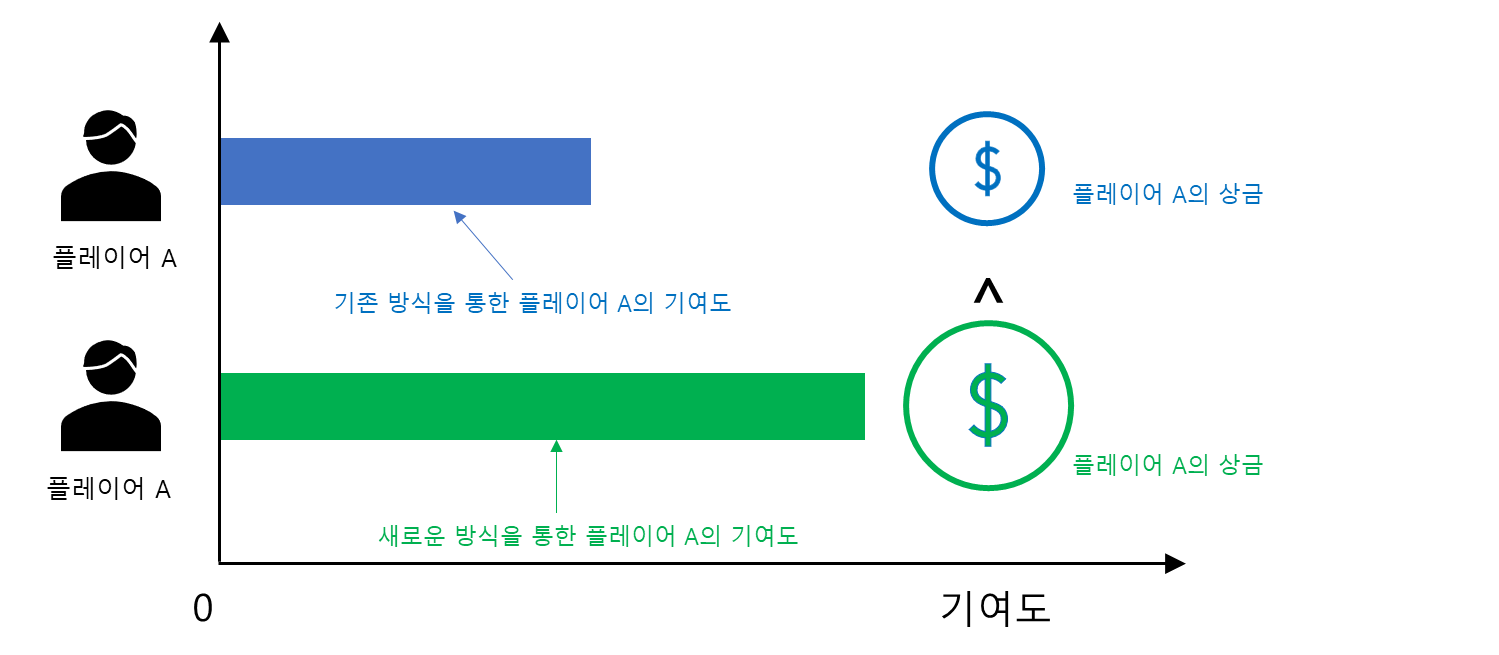
이를 수식으로 나타내면 다음과 같다.
$$v^i(S) \geq w^i(S) \;\; \text{for all}\;\; S \subset N \Rightarrow \phi_i(v, N) \geq \phi_i(w, N) \tag{6}$$
위 성질을 만족하는 분배 과정을 강한 단조성(Strong Monotonicity)을 갖는다고 한다.
(5) 가산성(Additivity)
만약 어떤 플레이어가 두 게임에 기여하여 얻은 총상금은 각 게임에서 기여함으로써 얻은 상금의 합과 일치해야 할 것이다.

이를 수식으로 나타내면 다음과 같다.
$$\phi_i(u+w, N) = \phi_i(u, N) + \phi_i(w, N)$$
2) Shapley Value의 수학적 정의
이제 Shapley Value를 소개할 시간이다.
먼저 $R$을 $N$이 가질 수 있는 임의의 순열이라고 하자. 그리고 $S^R_i$을 주어진 순열 $R$에 대하여 $i$ 앞에 있는 원소들의 집합이라고 하자. 이때 $i$에 대한 Shapley Value의 수학적 정의는 다음과 같다.
$$\phi_i = \frac{1}{|N|!}\sum_R \left [v(S^R_i \cup\{ i\}) - v(S^R_i)\right] \tag{7} $$
이때 $v(\emptyset) =0$이다. Summation(합)의 안쪽 부분이 $i$의 기여도임을 주목하자.
사실 분배 방법은 Shapley Value 말고도 다른 것들이 많이 있다. 예를 들어 $\phi_i = v(N)/|N|$, 즉 총상금을 기여도의 상관없이 모든 플레이어에게 $n$ 빵 하는 방법도 있다.
그렇다면 Shapley Value를 소개한 이유가 뭘까? 그것은 바로 앞에서 소개한 공정한 분배 성질을 즉, 효율성, 위장 플레이어, 대칭성, 강한 단조성을 Shapley Value는 모두 만족하기 때문이다. 증명은 섹션 4)에서 옵션으로 남겨둔다.
3) 예제를 통해 알아보는 Shapley Value
Shapley Value의 계산 원리를 알아보자. 먼저 5명의 플레이어가 있다고 하자. 즉, $N=\{1, 2, 3, 4, 5 \}$이다. 이때 Shapley Value는 모든 순열 $R$에 대해서 계산된다. 이때 $1$의 Shapley Value의 계산 과정을 살펴보자.
아래 그림은 $R = (1 \;\;2\;\; 3\;\; 4\;\; 5)$인 경우의 플레이어 $1$의 기여도를 계산하는 과정이다.

위와 같은 과정을 모든 순열 $R$에 대해서 계산한다. 그렇다면 총순열의 개수는 $|N|!$이 되고 Shapley Value는 이러한 기여도의 평균을 계산한 것이다.
(7)의 정의를 좀 더 단순화할 수 있다. $R = (1 \;\;2\;\; 3\;\; 4\;\; 5)$이라고 할 때 플레이어 $3$의 기여도를 계산한다고 해보자. 이때 (8)의 정의를 이용하면
$$v(S_3^R \cup {3}) - v(S_3^R) = v(\{1, 2, 3 \}) - v(\{ 1, 2\})$$
를 계산해야 할 것이다. 이때 $S = \{1, 2\}$라 하면 위 식은 다음과 같이 바꿔 쓸 수 있다.
$$v(S \cup \{3\}) - v(S)$$
그러면 $v(S \cup \{3\}) - v(S)$이 모든 순열 속에서 몇 번 나타나는지 살펴보자.

따라서 (7)은 다음과 같이 쓸 수 있다.
$$\phi_i = \frac{1}{|N|!}\sum_{S\subset N-\{i\}} |S|!(|N|-|S|-1)! \left [ v(S\cup \{i\}) - v(S) \right ] \tag{8}$$
보통 사람들은 (8)의 정의가 더 익숙할 것이다. 하지만 (7)의 정의를 알면 분모를 왜 $|N|!$으로 나누어주는지 직관적으로 알 수 있어서 좋다.
4) 증명
※주의※
수식만 보면 토가 나오는 사람들은 가던 길 가는 것이
정신건강에 좋다는 점을 미리 말씀드립니다.
(1) 효율성(Efficiency)
$$\begin{align} \sum_{i=1}^n\phi_i &= \sum_{i=1}^n\sum_R \left [ v(S_i^R \cup \{i\}) - v(S_i^R) \right]/|N|! \\ &= \sum_{R}\sum_{i=1}^n \left [ v(S_i^R \cup \{i\}) - v(S_i^R) \right]/|N|! \\ &= \sum_{R} \left [ v(N) - v(\emptyset) \right] /|N|! = \sum_R v(N)/|N|! = |N|! \frac{1}{|N|!}v(N) = v(N) \end{align}$$
(2) 위장 플레이어(Dummy Player)
$$\begin{align} v^i(S) &=v(S\cup \{i\})-v(S)=0 \;\;\text{for all} \;\; S \subset N-\{i\} \\ &\Rightarrow \phi_i = \frac{1}{|N|!}\sum_{S\subset N-\{i\}} |S|!(|N|-|S|-1)! \left [ v(S\cup \{i\}) - v(S) \right ] = 0 \end{align}$$
(3) 대칭성(Symmetry)
$v^i(S) = v^j(S) \;\;\text{for all } \;\; S\subset N-\{i, j\}$를 가정하고
$$c(S) = \frac{|S|!(|N|-|S|-1)! }{|N|!} $$
라고 하자.
$$\begin{align} \phi_i &= \sum_{S\subset N-\{i\}} c(S)\left [ v(S\cup \{i\}) - v(S) \right ] \\ &= \sum_{j\notin S\subset N-\{i\}} c(S)\left [ v(S\cup \{i\}) - v(S) \right ] + \sum_{j\in S\subset N-\{i\}} c(S)\left [ v(S\cup \{i\}) - v(S) \right ] \\ &= \sum_{i\notin S\subset N-\{j\}} c(S)\left [ v(S\cup \{j\}) - v(S) \right ] + \sum_{j\in S\subset N-\{i\}} c(S)\left [ v(S'_j\cup \{i, j\}) - v(S'_j \cup \{j\}) \right ] \\ &= \sum_{i\notin S\subset N-\{j\}} c(S)\left [ v(S\cup \{j\}) - v(S) \right ] + \sum_{i\in S\subset N-\{j\}} c(S)\left [ v(S'_i\cup \{j, i\}) - v(S'_i \cup \{i\}) \right ] \\ &= \sum_{i\notin S\subset N-\{j\}} c(S)\left [ v(S\cup \{j\}) - v(S) \right ] + \sum_{i\in S\subset N-\{j\}} c(S)\left [ v(S\cup \{j\}) - v(S) \right ] \\ &= \sum_{S\subset N-\{j\}} c(S)\left [ v(S\cup \{j\}) - v(S) \right ] = \phi_j \end{align}$$
여기서 $S'_j = S-\{j\}$이다.
(4) 강한 단조성(Strong Monotonicity)
$v^i(S) = v(S\cup \{i\}) - v(S)$라 하고 $v^i(S) \geq w^i(S) \;\; \text{for all}\;\; S \subset N$라고 가정하자.
$$\begin{align}\phi_i(v, N) = \sum_{S\subset N-\{i\}} c(S)v^i(S) \geq \sum_{S\subset N-\{i\}} c(S)w^i(S)= \phi_i(w, N) \end{align}$$
(5) 가산성(Additivity)
$$\begin{align}\phi_i(v+w, N) &= \sum_{S\subset N-\{i\}} c(S)(v+w)^i(S) \\ &= \sum_{S\subset N-\{i\}} c(S)\left [ v(S\cup \{i\}) - v(S) + w(S\cup \{i\}) - w(S) \right ] \\ &= \phi_i(v, N) + \phi_i(w, N) \end{align}$$
이때 두번째 등식에서 가치 함수의 선형성 성질을 사용했다.
2. SHAP란?
1) 정의
SHAP는 SHapley Additive exPlanation의 준말로 글로벌한 변수 중요도뿐만 아니라 개별 예측값에 대한 각 변수들의 영향력을 모형 클래스에 상관없이(Model-Agnostic) Additive 하게 배분하는 방식이다. 이때 영향력을 측정하는 값으로 Shapley Value를 사용한다. 또한 변수 중요도로써 가져야 할 바람직한 성질을 갖고 있어 인간이 생각하는 것과 유사한 해석을 제공한다.
이 말의 뜻을 하나하나 살펴보자.
(1) SHAP는 모형 클래스에 상관없이(Model-Agnostic) 개별 예측에 대한 Additive 한 해석 방법을 제공한다.
먼저 데이터 $(x_i, y_i)$가 있다고 하자. 여기서 $x_i=(x_{i1}, \ldots, x_{ip}) \in \mathbb{R}^p$인 $p$차원 입력 벡터이고 $y_i \in \mathbb{R}$인 실수 출력값이다.
위 데이터를 학습하여 얻은 예측 모형 $f$가 있다고 해보자. 이러한 $f$는 회귀 문제인 경우 선형 모형일 수도 있고 비선형인 복잡한 모형일 수도 있다. 또한 분류 문제인 경우는 특정 클래스에 속할 확률이 될 수도 있다. 이제 주어진 $x = (x_1, \ldots, x_p)$(학습 데이터에 포함된 것일 수도 있고 아닐 수도 있다)에 대하여 개별 예측값을 $f(x)$라 하자.
SHAP는 개별 예측값을 다음과 같은 선형 구조를 통해 직관적인 해석을 제공한다.
$$f(x) = \phi_0 + \phi_1 t(x)_1 + \cdots +\phi_p t(x)_p\tag{9}$$
여기서 $t : \mathbb{R}^p \rightarrow \mathbb{R}^p$로 주어진 $x$를 변환하는 매핑 함수이다. 즉,
$$t(x) = (x'_1, \ldots, x'_p), \;\; \text{where} \;\; x'_j = t(x)_j$$
그리고 $\phi_k, k=0, \ldots, p$는 실수이다.
이제 (9)의 구조를 확인해보자. 먼저 매핑 $t$의 정체가 궁금해질 것이다. 만약 $t(x) = x$라 해보자. 이는 결국 선형 회귀 모형을 학습한 것과 같으며 모형 클래스가 선형 회귀 모형에 한정된 구조가 된다. 따라서 모형에 상관없는(Model-Agnostic) 구조를 만들기 위하여 오리지날 변수 $x$가 아닌 $t(x)$를 도입하게 된 것이다.
다음으로 (9)가 $p$개의 변수로 이루어진 선형 모형인 것에 주목하자. 선형 모형을 도입한 이유는 개별 예측에 대한 해석을 쉽게 하기 위함이다.
그렇다면 왜 $p$개의 변수로 이루어진 것일까?
이에 대한 답이 SHAP의 핵심인 것이다. 먼저 다음과 같은 매핑 $t$를 생각해보자.
$$t(x)_j = \begin{cases} 1 & \text{if} \;\; x_j \text{ is not missing} \\ 0 & \text{if} \;\; x_j \text{ is missing} \end{cases} $$
즉, $x_j$가 결측이 아닌 관측된 값이 있다면 $t(x)_j = 1$이고 아닌 경우는 $t(x)_j=0$이다. 이제 $x'_j = t(x)_j$라 하고 (9)를 다음과 같이 바꿔보자.
$$f(x) = \phi_0 + \phi_1 x'_1 + \cdots +\phi_p x'_p\tag{10}$$
여기서 $\phi_j, j=1, \ldots, p$를 $x_j$가 개별 예측값 $f(x)$에 미치는 영향을 수치화한 것이라고 해보자. 그렇다면 주어진 $x$가 결측이 하나도 없는 경우에는
$$f(x) = \phi_0+\phi_1 +\cdots +\phi_p$$
가 되고 이는 개별 예측치가 각 변수의 영향력의 합으로 표현된다는 것이다. 즉, 각 변수의 영향력을 개별적인 합으로 표현하기 위하여 $p$개의 변수로 이루어진 선형 모형을 사용한다는 것이다.
이를 좀 더 일반화하면 SHAP은 특정 변수의 존재(결측) 유무에 따른 개별 예측값을 실제로 존재하는 변수만의 영향력의 합으로(Additive) 표현된다는 것이다.
예를 들어 설명 변수 4개를 이용하여 예측 모형 $f$를 학습했다고 하자. 이때 (학습 데이터가 아닌) 새롭게 주어진 입력 변수 벡터가 $x_\text{test} = (1.1, NA, NA, 3)$이라고 해보자($NA$는 결측을 의미한다). 이 경우 $x' = (1, 0, 0, 1)$이 되고
$$f(x) = \phi_0+\phi_1+\phi_4$$
가 되고 결국 $x$에서 존재하는 변수들의 영향력으로 표현된 것이다($\phi_0$는 어떤 상황에서든 기본적으로 깔고 가는 값이다). 이는 지극히 상식적이다. $x_{\text{test}, 2}, x_{\text{test}, 3}$가 개별 예측값을 계산하는 데 사용되지 않았으므로 $x_2, x_3$에 대한 영향력은 제거되는 것이 공정하기 때문이다.
주의해야 할 점은...
위 예제에서는 실제로 설명 변수 4개($x_i=(x_{i1}, \ldots , x_{i4})$)인 학습 데이터를 이용하여 예측 모형 $f$를 얻었지만 새로운 데이터에서는 2번째와 3번째 변수($x_{\text{test}, 2}, x_{\text{test}, 3}$)가 결측이 되었다는 점이다. 가령 이에 대해서 예측 모형 $f$에 $x_2=x_3=0$을 집어넣는 것과 헷갈리는 분들이 있는데 그게 아니라 결측, 즉 예측값을 구하는 데 사용할 수 없는 상태인 것이다(0을 집어넣는 행위가 이미 결측이 아닌 것이다). 결측이 존재하는 변수가 섞여 있는 경우 예측값을 구하는 방법은 다음 섹션에서 설명한다.
(2) SHAP는 영향력을 측정하는 값으로 Shapley Value를 사용한다.
SHAP는 영향력을 측정하는 값으로 Shapely Value를 사용한다고 했다. 이에 대한 설명을 위해서 예측 모형의 학습 문제를 상금 분배 문제로 표현해보자.
$x = (x_1, \ldots, x_p) \in \mathbb{R}^p$를 $p$명의 플레이어라고 하면 주어진 $x$에 대한 (학습된 예측 모형 $f$의) 예측값
$$f(x) = f(x_1, \ldots, x_p)$$
는 $p$명의 플레이어가 활약하여 얻은 상금이라고 할 수 있다. 여기서 $f$는 앞에서 살펴본 가치 함수 $v$와 비슷한 역할을 하는 것이다.
기억을 되살려야 할 때이다...
$v$는 모든 플레이어뿐만 아니라 일부 플레이어에 대해서도 정의가 되었다는 사실을 기억해야 한다. 그렇다면 $f$도 일부의 변수(결측 된 변수가 있다는 것이다)를 이용해서 값을 구할 수 있어야 한다. 극단적으로 $x$가 모두 결측이라고 해보자. 이 경우 예측값을 무엇으로 하는 것이 일반적이고 상식적일까?
우리가 $y_i$만 있고 $x_i$가 없는 경우의 회귀 모형을 생각한다고 하면 제곱 손실 관점에서 최적화된 추정치는 $y_i$의 평균인 $\bar{y} = \sum_{i=1}^ny_i/n$이 된다.
$$\DeclareMathOperator*{\argminA}{arg\,min} \bar{y} = \argminA_{c\in \mathbb{R}} \sum_{i=1}^n(y_i-c)^2$$
마찬가지로 $x$가 모두 결측인 경우 학습 데이터의 $y_i$의 평균을 생각해볼 수 있지만 다행스럽게도 학습 데이터 안에는 $x_i$들이 있다($x$는 학습 데이터에 포함되지 않은 데이터라고 생각하자). 이때 $n$개 모두 사용할 수도 있지만 학습 데이터에서 $k$개를 샘플링하여 사용할 수도 있다. 이때 붓스트랩 추출 또는 비 복원 추출 모두 가능할 것으로 판단된다(관련 자료를 찾지 못했으나 Marginalization 개념상 붓스트랩으로 하는 것이 자연스러워 보이며 학습 데이터에서 중복된 행이 있을 가능성이 보통은 작으므로 비복원 추출도 가능하다고 생각한다).
샘플링된 $k$개 데이터의 행 번호를 $r_1, \ldots, r_k(1\leq r_i \leq n, \;\forall i=1, \ldots, k)$라 할 때 $x$가 모두 결측인 경우에는 예측값을 다음과 같이 할당한다.
$$f(NA, \ldots, NA) = \frac{1}{k}\sum_{i=1}^kf(x_{r_i}) \tag{11}$$
(11)을 $f$의 Expected Value라고 하겠다(이 값은 $\phi_0$의 추정값과 동일하며 Base Value라고도 한다). 사실 엄밀한 의미에서의 기대값은 아니고 학습 데이터의 샘플로 근사한 기대값이 된다.
$P=\{ j \in \{1, 2, \ldots, p\} | x_j \text{ is not missing}\}$은 결측이 아닌 변수의 인덱스(플레이어) 총집합, $S \subset P$는 $P$의 임의의 부분 집합이라 하자. $S=\emptyset$도 포함된다.
하지만 $f$를 그 자체로 가치 함수 $v$로 두기에는 아직 불완전하다. 왜냐하면 $f(x) = v(S)$라 할 경우 일반적으로
$$ f(NA, \ldots, NA) = v(\emptyset) = \frac{1}{k}\sum_{i=1}^kf(x_{r_i}) \neq 0\tag{12}$$
즉, $v(\emptyset) \neq 0$이 되기 때문이다. 따라서 $v(\emptyset) = 0$을 만족시키기 위해 $v$를 다음과 같이 정의한다.
$$v(S) = f(x) - \frac{1}{k}\sum_{i=1}^kf(x_{r_i}) , \;S\subset P \tag{13}$$
이렇게 정의하면 $v(\emptyset) = 0$이 된다.
아직 끝나지 않았다...
$S=\emptyset$, 즉 $x$가 모두 결측인 경우에 대하여 예측값을 계산했지만 일부만 결측이 된 경우에는 어떻게 해야 할지 대책을 마련해야 한다.
이를 위해 사전에 몇 가지 정의를 해보자.
$S$에 대하여 $x_S$를 결측이 아닌 변수들의 집합이라 하고 $f_S$를 다음과 같이 정의한다.
$$f_S(x_S) = f(x_S, x_{S^c})$$
예를 들어 $x=(x_1, x_2, x_3)$이고 $S=\{2 , 3\}$이라 하면
$$f_S(x_S) = f(NA, x_2, x_3)$$
이 되는 것이다.
이제 $f_S(x_S)$는 다음과 같이 $x_S$가 주어진 경우의 $f(x)$의 조건부 기대값을 고려한다.
$$f_S(x_S) = E(f(x_S, X_{S^c})|x_S) = \int f(x_S, x_{S^c})p(x_{S^c}|x_S) dx_{S^c} \tag{14}$$
(14)에서 중요한 건 조건부 확률 밀도 함수 $p(x_{S^c}|x_S)$를 모른다는 것이며 학습 데이터를 통한 샘플을 통해서도 근사하기 어렵다. 왜냐하면 $x_S$가 학습 데이터에 포함되어 있을지도 미지수이며(연속형이 포함되어 있는 경우를 생각해보자) 설령 있다고 하더라도 $x_S$로 한정시키게 되면 조건부 확률 밀도 함수를 계산할 수 있는 샘플수가 급격히 감소하여 제대로 근사를 할 수 없기 때문이다(아래 그림 참고).

이에 변수 간의 독립성을 가정하게 된다. 즉,
$$p(x_{S^c}|x_S) = p(x_{S^c})$$
이 되고 이를 (14)에 적용하면 다음과 같다(Marginalization).
$$f_S(x_S) = \int f(x_S, x_{S^c})p(x_{S^c}) dx_{S^c} (\approx E(f(x_S, X_{S^c})|x_S)) \tag{15}$$
물론 정확한 $ p(x_{S^c})$를 모르지만 대신 샘플 수를 최대 $n$(학습 데이터 개수) 개까지 사용할 수 있다는 것이다. 학습 데이터에서 $k$개를 랜덤 추출(샘플링)된 행(row)들을 $x_{r_1}, \ldots, x_{r_k}$라 하자. 그렇다면 $x_{r_i}$에 있는 변수들은 $S$에 포함되거나 안되거가 둘 중 하나일 것이다. 즉,
$$x_{r_i} = (x_{r_i, S}, x_{r_i, S^c})$$
이제 주어진 $x_S$에 대하여 $x_{S^c}$를 학습 데이터에서 샘플링된 것으로 대체한 뒤 (15)를 다음과 같이 계산한다(정확히 말하면 학습 데이터로 근사하는 것이다).
$$ f_S(x_S) = \frac{1}{k}\sum_{i=1}^kf(x_S, x_{r_i, S^c}) (\approx \int f(x_S, x_{S^c})p(x_{S^c}) dx_{S^c}) \tag{16}$$
최종적으로 $f_S(x_S)$는 (16)으로 계산하게 된다. 이 계산을 위해 우리는 두 번의 근사를 수행했다. 하나는 독립 가정으로 인한 근사, 다른 하나는 학습 데이터를 통한 샘플링 근사이다.
아래 그림은 $f_S(x_S)$를 계산하는 예제이다.

이제 $f_S(x_S)$의 계산법을 확실히 알았으니 (8)과 (13)을 이용하여 Shapley Value를 다시 써보자.
$$\begin{align} \phi_i(f, x) &= \frac{1}{|P|!}\sum_{S\subset P-\{i\}} |S|!(|P|-|S|-1)! \left [ f_{S\cup \{i\}}(x_{S \cup \{ i \} }) - c - (f_S(x_S) - c) \right ] \\ &= \frac{1}{|P|!}\sum_{S\subset P-\{i\}} |S|!(|P|-|S|-1)! \left [ f_{S\cup \{i\}}(x_{S \cup \{ i \} }) - f_S(x_S) \right ] \\ &\text{for } \; i = 1,\ldots, p \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; (17) \end{align}$$
여기서
$$c = \frac{1}{k}\sum_{i=1}^kf(x_{r_i})$$
이며 $\phi_0 = c$이다.
기존 Shapley Value와 구분하기 위해 (17)에서 정의된 값을 SHAP Value라 한다.
아래 그림은 주어진 입력 벡터 $x = (NA, 4, 3, NA)$에 대하여 SHAP Values를 계산하는 과정이다.
이제 아래 그림을 통하여 SHAP Value 계산 과정을 이해할 수 있다. $\phi_1$은 Summation 안쪽에
$$f_{S\cup \{1\}}(x_{S\cup \{i\}}) - f_S(x_S)$$
가 모든 $S$에 대하여 0이 되므로 $\phi_1=0$이다. 마찬가지로 $\phi_4=0$이다. 이때 $x_j = NA$이면 $\phi_j = 0$임을 유추할 수 있는데 이에 대한 내용은 아래에서 다룬다(Missingness). 그리고 $\phi_2$에 대한 계산 과정도 그림에 포함되어 있다. 연습 삼아 $\phi_3$도 손으로 써서 계산해보자.

그런데...
SHAP를 제안한 Lundberg와 Su-In Lee는 오리지날 변수 $x$가 아닌 변수의 결측 유무를 나타내는 단순화된 변수(Simplified Input) $x'$을 이용하여 Shapley Value를 나타내었다. 이렇게 하는 이유는 개별 예측값에 대한 변수들의 총영향력을 변수들의 결측 유무로 표현하여 단순하고 직관적인 해석 모형을 제공하고 싶었기 때문이다.
논문에서는 $h_x : \{0, 1 \}^p \rightarrow \mathbb{R}^p$인 매핑을 통하여 $x'$과 $x$의 관계를 다음과 같이 설정하고 있다.
$$x = h_x(x')$$
(9)에서 $t = h_x^{-1}$라고 생각하면 된다($h_x$는 치역이 한 포인트 벡터 $x$이기 때문에 1대 1 대응 함수이므로 역함수가 존재한다).
사실 $h_x$의 명확한 수식이 있는 것은 아니고 단순화된 입력 값을 원래의 오리지날 변수로 변환해주는 것이라고만 이해하면 된다(사실 이 부분이 이해가 정말 안됐다). 예를 들어보자. $x = (x_1, NA, x_3, x_4)$에 대한 예측값을 구하는 문제에서 $x' = (1, 0, 1, 1)$로 표현된다. 그렇다면 $h_x$은 $x'$ 원소가 1인 인덱스에 대하여 원래의 값으로 다시 되돌려주는 매핑인 것이다.
또한 $z' = (z_1', \ldots, z_p') \in \{0, 1 \}^p$은 $z'_j\leq x'_j, j=1, 2, \ldots, p$인 임의의 벡터이다. 이때 $z'$를 $x'$의 협력체 벡터(Coalition Vector)라 하고 이를 $z'\subset x'$이라 표현하겠다.
$h_x$는 $z'$에 대해서도 오리지날 변수 공간으로 변환하는 데 그 과정은 아래 그림을 보면 이해할 수 있다.
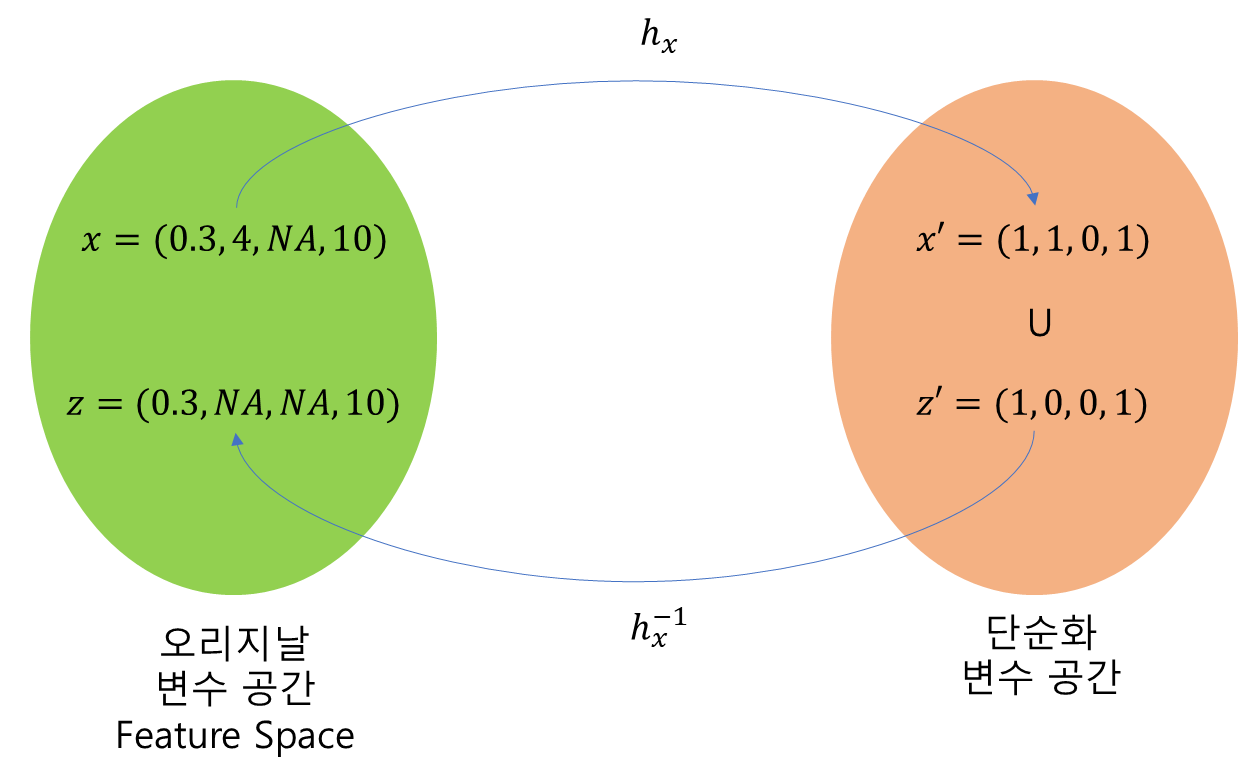
이러한 세팅을 이용하여 (17)의 SHAP Value를 다음과 같이 바꿔준다.
$$\phi_i(f, x) = \sum_{z'\subset x'}\frac{|z'|!(p-|z'|-1)!}{p!}[f_x(z')-f_x(z'-\{i\})] \tag{18}$$
여기서 $|z'|$은 $z'$에서 1인 원소의 개수, $f_x(z') = f(h_x(z'))$이고 $z'-\{i\}$는 $z'_j = 0$으로 세팅한다는 뜻이다.
이렇게 정의된 $\phi_j, j=1, \ldots, p$는 개별 예측값에 대한 $j$번째 변수의 영향력을 나타내게 된다.
(3) SHAP는 변수 중요도로써 가져야 할 바람직한 성질을 갖고 있다.
SHAP의 배분 방식을 통해 얻어진 변수 중요도는 Local Accuracy, Missingness, Consistency 성질을 만족한다. 이게 왜 바람직한 성질인지 알아보자.
Property 1. Local Accuracy
개별 예측값 $f(x)$을 단순화된 입력 $x'$으로 이루어진 해석이 쉬운 모형(Explanation Model : EM) $g(x')$를 도입하여 근사한다. 여기에 담긴 철학은 $f(x)$와는 조금 차이가 발생하더라도($f(x) \approx g(x')$) 해석을 쉽게 하자는 취지이다($g(x') = \phi_0 + \sum_{j=1}^p\phi_j x'_j$).
이때 $f(x) = g(x')$라면 $g$를 통해 해석력을 높이는 것뿐만 아니라 개별 예측값과도 정확히 일치하는 상황이 되므로 이는 변수 중요도로써 아주 이상적인 상황이 된다. 이러한 성질을 Local Accuracy라 하며 수학적 정의는 다음과 같다.
$$x = h_x(x') \Rightarrow f(x) = g(x') = \phi_0 + \sum_{j=1}^p\phi_j x'_j \tag{19}$$
여기서$\phi_0 = \frac{1}{k}\sum_{i=1}^kf(x_{r_i})$이다.
주의할 점은 $z' \subset x'$에 대해서는 위 성질을 만족하지 않을 수 있다. Local Accuracy는 Shapley Value의 성질인 효율성(Efficiency)과 비슷하다.
Property 2. Missingness
이는 앞에서 다룬 Shapley Value의 성질 위장 플레이어(Dummy Player)와 비슷한 개념이다. Missingness는 특정 변수가 결측 되었다면 해당 변수 영향력은 없다는 것이다. 이를 수식으로 표현하면 다음과 같다.
$$x'_j = 0 \Rightarrow \phi_j = 0 \tag{20}$$
사실 $x'_j = 0$이면 $\phi_j \cdot x'_j = \phi_j \cdot 0 = 0$이므로 $\phi_j$가 어떤 값을 가져도 개별 예측값에 영향을 주지 못한다. 하지만 그중에서 $\phi_j=0$을 만족한다면 소위 위장 플레이어(Dummy Player)와 같은 해석을 할 수 있어서 이는 인간의 상식에 비추어 볼 때 합리적이 되는 것이다.
Property 3. Consistency
이는 앞에서 다룬 Shapley Value의 강한 단조성(Strong Monotonicity)과 정확히 일치한다. Consistency는 하나의 예측 모형에서 더 큰 기여를 했다면 그 영향력이 적어도 줄어들진 않는다는 것이다.
$$f^1_x(z') - f^1_x(z'- \{i\}) \geq f^2_x(z') - f^2_x(z'-\{i\}) \;\;\text{ for all }\;\;z'\subset x' \\ \Rightarrow \phi_i(f^1, x) \geq \phi_i(f^2, x) \tag{21} $$
Property 1~3의 증명은 앞에서 Shapley Value의 성질을 증명했던 방법을 이용하면 쉽게 증명되므로 생략한다.
3. SHAP 종류
SHAP에도 여러 가지 종류가 있는데 이에 대해서 알아보자.
1) Linear SHAP
a. 정의
$f$가 선형 회귀 모형인 경우의 SHAP을 적용한 것이 Linear SHAP이다. 이 경우 굉장히 간단하게 SHAP Value를 구할 수 있다.
먼저 학습 데이터 $(x_i, y_i)$($x_i = (x_{i1}, \ldots, x_{ip})$)를 이용하여 얻어진 선형 회귀 모형이 다음과 같다고 하자.
$$f(x) = b_0 + b_1x_1 + \cdots + b_px_p$$
$x=(x_1, \ldots, x_p)$는 새로운 데이터를 포함하는 입력 벡터이다. $x_i$는 학습 데이터의 $i$번째 행(row)을 의미하므로 헷갈리지 말자.
이제 주어진 데이터 $x$에 대해서 SHAP Value는 다음과 같이 계산된다.
$$\phi_0(f, x) = \frac{1}{k}\sum_{i=1}^kf(x_{r_i}), \\ \phi_j(f, x) = \begin{cases} b_j\left(x_j-\frac{1}{k}\sum_{i=1}^nx_{r_i, j} \right ) & \;\; x_j \text{ is present} \\ 0 & \;\; x_j \text{ is missing}\end{cases} \tag{22}$$
여기서 $x_{r_i} = (x_{r_i, 1}, \ldots, x_{r_i, p})$이며 결측이 존재하는 경우에 조건부 표본 평균을 계산하기 위해 샘플링된 데이터이다.
b. 증명
(22)의 증명을 해보자. 먼저 $S \subset P-\{j\}$에 대하여 $S' = S\cup \{j\}$이라 하자. 이때 다음을 만족한다.
$$ f_{S'}(x_{S'}) - f_S(x_S) = \begin{cases} b_j\left ( x_j - \frac{1}{k}\sum_{i=1}^k {x_{r_i, j}} \right ) &\;\; x_j \text{ is present} \\ 0 &\;\; x_j \text{ is missing} \end{cases}$$
이는 모든 $S \subset P-\{j\}$에 대하여 성립한다. 또한 어느 경우도 $f_{S'}(x_{S'}) - f_S(x_S)$는 $S$에 의존하지 않으므로 이를 $f_{S'}(x_{S'}) - f_S(x_S)=c$라 하자. 그러면
$$\begin{align} \phi_j(f, x) &= \frac{1}{|P|!}\sum_{S\subset P-\{j\}} |S|!||P|-|S|-1|! \left [ f_{S\cup \{j\}}(x_{S \cup \{ j \} }) - f_S(x_S) \right ] \\ &= c \frac{1}{|P|!}\sum_{S\subset P-\{j\}}|S|!|P|-|S|-1|! \\ &= c\frac{1}{|P|!}|P|! = c \end{align} $$
c. Python 구현
이제 Linear SHAP을 구현해보자. 여기서는 내가 구현한 것과 SHAP 관련 패키지 shap의 결과와 비교해보고자 한다.
먼저 LinearShap 클래스를 정의한다. 초기화할 때 fit을 이용하여 적합을 이미 완료한 LinearRegression 클래스를 받도록 했고 $\phi_0$나 결측이 포함된 $x$에 대한 예측을 수행하기 위한 data를 넘겨줘야 한다. 그리고 SHAP value를 계산하는 shap_values 함수, 예측을 수행하는 predict 함수도 정의해주었다. 이때 predict 함수는 입력 벡터에 결측이 포함된 경우에도 계산 가능하도록 구현하였다.
import pandas as pd
import numpy as np
import shap
from sklearn.linear_model import LinearRegression
class LinearShap():
def __init__(self, lm, data):
self.lm = lm
self.data = data
self.phi_0 = None
self.phi_ = None
def shap_values(self, x):
lm = self.lm
data = self.data
self.phi_0 = np.mean(lm.predict(data))
phi_ = []
for i, val in enumerate(x):
if pd.isna(val):
phi_.append(0)
else:
phi_.append(lm.coef_[i]*(val - np.mean(data[:, i])))
self.phi_ = phi_
return (self.phi_0, self.phi_)
def predict(self, x):
data = self.data.copy()
if len(np.where(pd.isna(x))[0]) == 0:
return self.lm.predict(x)[0]
else:
x = x.flatten()
idx = np.where(~pd.isna(x))[0]
data[:, idx] = x[idx]
return np.mean(self.lm.predict(data))
다음으로 예제용 데이터를 만들고 이를 이용하여 선형 회귀 모형을 학습한다. 그리고 $\phi_0$나 결측이 포함된 $x$에 대한 예측을 수행하기 위해 학습 데이터로부터 데이터를 샘플링한다.
np.random.seed(10)
## 데이터 생성
x1 = np.array([3, 7, 3, 3, 6, 2, 9])
x2 = np.array([1, 9, -5, 7, 10, -2, 5])
y = 4*x1 + 2*x2 + 1
X = np.column_stack([x1, x2])
## 선형 회귀 모형 적합
linear_model = LinearRegression().fit(X, y)
## 결측 처리를 위한 데이터 샘플 추출
sampled_row = np.random.choice(range(len(y)), size=5)
data = X[sampled_row, :]
## LinearShap 클래스 초기화
linear_shape = LinearShap(linear_model, data)
- 결측 값이 포함되지 않은 경우 -
이제 SHAP Value를 구하고 이 값들의 합이 개별 예측값과 일치하는지도 살펴보자.
x = np.array([2, 1])
linear_shape.shap_values(x)
print('Expected Values :', linear_shape.phi_0)
print('Shap Values :', linear_shape.phi_)
print('Prediction Value : ', linear_shape.predict(np.expand_dims(x, axis=0)))
print('Sum Phi : ', linear_shape.phi_0+np.sum(linear_shape.phi_))

결과를 보니 $\phi_0 = 31.8, \phi_1 = -12, \phi_2 = -8.8$이고 이들의 합이 개별 예측값(Prediction Value)과 일치하였다.
$$f(x) - \phi_0 = 11 - 31.8 = -12 + (-8.8) = \phi_1 + \phi_2$$
이를 해석하자면 예측값 11과 $\phi_0 = 31.8$의 차이인 -20.8에 대하여 $x_1$가 -12만큼 기여를 했고 $x_2$가 -8.8만큼 기여했다는 뜻이 된다.
이번엔 shap 패키지를 이용하여 SHAP Value를 구해보자.
explainer = shap.LinearExplainer(linear_model, data)
shap_values = explainer.shap_values(x)
print('Expected Values :', explainer.expected_value)
print('Shap Values :', shap_values)

구현한 클래스가 결과와 정확하게 일치하였다.
- 결측값이 포함된 경우 -
이번엔 결측이 포함된 경우에 대하여 같은 작업을 반복해보자.
x = np.array([np.nan, 1])
linear_shape.shap_values(x)
print('Expected Values :', linear_shape.phi_0)
print('Shap Values :', linear_shape.phi_)
print('Prediction Value : ', linear_shape.predict(np.expand_dims(x, axis=0)))
print('Sum Phi : ', linear_shape.phi_0+np.sum(linear_shape.phi_))

$\phi_0 = 31.8, \phi_1 =0, \phi_2 = -8.8$이고 이들의 합과 개별 예측값이 일치했다(아주 작은 소수점 차이는 덧셈 과정에서 발생한듯하다).
그러나 결측이 포함된 경우는 shap 패키지에서는 해당 SHAP Value를 0이 아닌 NaN으로 표시되었다.
shap_values = explainer.shap_values(x)
print('Expected Values :', explainer.expected_value)
print('Shap Values :', shap_values)

2) Exact SHAP
지금까지는 예측 모형이 선형 회귀 모형인 경우 SHAP Value의 공식을 통해 쉽게 구했지만 일반적인 경우에 대해서 정의(17)를 이용한 정확한 SHAP Value를 계산하는 것을 구현해보고자 한다.
Python 구현
이제 Exact SHAP을 구현해보자. 여기서는 내가 구현한 것과 SHAP 관련 패키지 shap의 결과와 비교해보고자 한다.
먼저 ExactShap 클래스를 정의한다. 초기화할 때 fit을 이용하여 적합을 이미 완료한 sklearn에서 제공하는 model 클래스를 받도록 했다. 이 model 클래스는 반드시 predict 메서드가 구현되어 있어야 한다. 다음으로 $\phi_0$나 결측이 포함된 $x$에 대한 예측을 수행하기 위한 data를 넘겨줌으로써 초기화가 마무리된다.
그리고 SHAP value를 계산하는 shap_values 함수, 예측을 수행하는 predict 함수도 정의해주었다. 이때 predict 함수는 입력 벡터에 결측이 포함된 경우에도 계산 가능하도록 구현하였다. 이 밖에도 주어진 리스트의 모든 부분 집합을 계산하는 powerset, $f_S(x_S)$를 계산하는 get_f_s 함수도 SHAP Value 계산할 때 필요하므로 구현해주었다.
import pandas as pd
import numpy as np
import shap
from math import factorial
from sklearn.linear_model import LinearRegression
class ExactShap():
def __init__(self, model, data):
self.model = model
self.data = data
self.phi_0 = None
self.phi_ = None
def powerset(self, l):
x = len(l)
res = []
for i in range(1 << x):
temp = [l[j] for j in range(x) if (i & (1 << j))]
res.append(temp)
return res
def get_f_s(self, x, s, data):
data_rep = data.copy()
model = self.model
if len(s) == 0:
return np.mean(model.predict(data_rep))
elif len(s) == data_rep.shape[1]:
x = np.expand_dims(x, axis=0)
return np.mean(model.predict(x))
else:
data_rep[:, s] = x[s]
return np.mean(model.predict(data_rep))
def shap_values(self, x):
model = self.model
data = self.data
self.phi_0 = np.mean(model.predict(data))
phi_ = []
missing_idx_set = set(np.where(pd.isna(x))[0])
for i, val in enumerate(x):
if pd.isna(val):
phi_.append(0)
else:
p = data.shape[1]
target_set = set(range(p))-{i}
if missing_idx_set:
target_set = target_set - missing_idx_set
p = p-len(missing_idx_set)
target_set = list(target_set)
all_subset = self.powerset(target_set)
temp_phi = 0
for s in all_subset:
temp_val = self.get_f_s(x, s+[i], data) - self.get_f_s(x, s, data)
temp_val = factorial(len(s))*factorial(p-len(s)-1)/factorial(p)*temp_val
temp_phi += temp_val
phi_.append(temp_phi)
self.phi_ = phi_
return (self.phi_0, self.phi_)
def predict(self, x):
data = self.data.copy()
if len(np.where(pd.isna(x))[0]) == 0:
x = np.expand_dims(x, axis=0)
return self.model.predict(x)[0]
else:
idx = np.where(~pd.isna(x))[0]
data[:, idx] = x[idx]
return np.mean(self.model.predict(data))
간단한 테스트 데이터를 만들고 이를 이용하여 예측 모형을 학습한다. 그리고 $\phi_0$나 결측이 포함된 $x$에 대한 예측을 수행하기 위해 학습 데이터로부터 데이터를 추출한다.
np.random.seed(10)
## 데이터 생성
x1 = np.array([3, 7, 3, 3, 6, 2, 9])
x2 = np.array([1, 9, -5, 7, 10, -2, 5])
y = 4*x1 + 2*x2 + 1
X = np.column_stack([x1, x2])
## 선형 회귀 모형 적합
lm = LinearRegression().fit(X, y)
## 결측 처리를 위한 데이터 샘플 추출
sampled_row = np.random.choice(range(len(y)), size=5)
data = X[sampled_row, :]
## ExactShap 클래스 초기화
exact_shap = ExactShap(lm, data)
- 결측값이 포함되지 않은 경우 -
SHAP Value와 이 값들의 합이 개별 예측값과 일치하는지 확인해보자.
x = np.array([1, 2])
exact_shap.shap_values(x)
print('Expected Values :', exact_shap.phi_0)
print('Shap Values :', exact_shap.phi_)
print('Prediction Value :', exact_shap.predict(x))
print('Sum Phi :', exact_shap.phi_0+np.sum(exact_shap.phi_))

SHAP Value와 Expected Value의 합과 개별 예측값이 정확하게 일치하였다. 이번엔 shap 패키지를 이용하여 SHAP Value를 구해보자. 여기에서는 Explainer 클래스를 사용한다.
explainer = shap.Explainer(lm, data)
shap_values = explainer.shap_values(x)
print('Expected Values :', explainer.expected_value)
print('Shap Values :', shap_values)

내가 구현한 것과 정확하게 일치했다.
- 결측값이 포함된 경우 -
이번엔 입력 벡터에 결측이 있는 경우의 예측값과 SHAP Value 그리고 이들의 합이 개별 예측값과 일치하는지 살펴보자.
x = np.array([np.nan, 2])
exact_shap.shap_values(x)
print('Expected Values :', exact_shap.phi_0)
print('Shap Values :', exact_shap.phi_)
print('Prediction Value :', exact_shap.predict(x))
print('Sum Phi :', exact_shap.phi_0+np.sum(exact_shap.phi_))

예상대로 개별 예측값과 SHAP Value와 Expected Value의 합과 정확하게 일치했다. 마찬가지로 shap 패키지에서도 동일한 SHAP Value와 Expected Value를 얻을 수 있다. 다만 결측이 있는 변수에 대해서 0이 아닌 NaN으로 리턴된다는 것을 유념하자.
explainer = shap.Explainer(lm, data)
shap_values = explainer.shap_values(x)
print('Expected Values :', explainer.expected_value)
print('Shap Values :', shap_values)

3) Kernel SHAP
a. 정의
SHAP Value $\phi_i, i=1, \ldots, p$를 계산하기 위해선 $S$의 모든 부분 집합에 대하여 $f_{S\cup \{i\}}(x_{S \cup \{ i \} }) - f_S(x_S)$을 계산해야 한다. 설명 변수(입력 벡터)의 차원이 계산량이 많아서 느려진다.
Lundberg와 Su-in Lee는 LIME(Local Interpretable Model-agnostic Explanations) 프레임워크를 이용하여 (약간의 정확성을 잃을 수도 있지만) 좀 더 빠르게 계산하도록 만든 것이 Kernel SHAP이다.
LIME에 대해서 간략히 소개하면 먼저 해석 가능 모형(Interpretable Model)들의 집합 $G$를 생각한다.
$$G = \{ g : g(z') = c_0+c_1z'_1+\cdots+c_pz'_p \}$$
이때 주어진 입력 벡터 $x$, 학습된 예측 모형 $f$에 대하여 LIME은 다음의 목적 함수를 최소화하는 $g\in G$를 찾는다.
$$\DeclareMathOperator*{\argminA}{arg\,min} \argminA_{g\in G} \left [ L(f, g, \pi_{x'}) + \Omega(g) \right ] $$
여기서
$$L(f, g, \pi_{x'}) = \sum_{z'\in Z} \pi_{x'}(z')(f_x(z') - g(z'))^2\tag{23}$$
이고 $f_x(z') = f(h_x^{-1}(z'))$, $Z = \{ z'\in \{0, 1\}^p \}$, $\pi_{x'}(z')$는 $x$의 단순화 변수(Simplified Input) $x'$과 $z'$의 거리의 반비례하는 커널(Kernel) 함수이다. 따라서 $L$은 $f_x(z')$을 잘 설명하는 가중 최소 제곱 모형 $g$를 찾기 위한 목적함수(가중 최소 제곱)인 것이다.
그리고 $\Omega(g)$는 모형의 $g$의 복잡도를 나타내는 값이며 이 값이 작을수록 해석하기 좋은 단순한 모형이라 할 수 있다. 따라서 LIME은 $f(x)$를 잘 근사하면서 해석력이 좋은 모형을 찾는 방법이라 할 수 있다.
Lundberg와 Su-in Lee는 SHAP Value 계산을 위해 LIME 프레임워크를 가져왔으며 특정 $\Omega$와 $\pi_{x'}$에 (23)의 해가 SHAP Value로 이루어진 해석 가능 모형에 수렴한다는 것을 보였다.
정리 (Shapley Kernel)
$x$를 $p$차원 입력 벡터(설명 변수 벡터)라 하고 학습된 예측 모형 $f$이 있다고 가정하자. 이때 $x'$의 협력체 벡터(Coalition Vector) $z'$에 대한 선형 모형 $g^*$가 다음과 같다고 하자. $$g^* = \phi_0+\phi_1z_1'+\cdots+\phi_pz_p'$$
여기서 $\phi_0$는 $f$의 Expected Value이고 $\phi_j, j=1, \ldots, p$는 SHAP Value이다. 또한 다음과 같이 세팅하자.
$$\begin{align} \Omega(g)&=0 \\ \pi_{x'}(z') &= \frac{|x'|-1}{\begin{pmatrix} |x'| \\ |z'|\end{pmatrix}|z'|(p-|z'|)} \\ L(f, g, \pi_{x'}) &= \sum_{z'\subset x'}\pi_{x'}(z')(f_x(z') - g(z'))^2, \;\;g \in G \end{align}\tag{24}$$
이때 $|z'|, |x'|$은 1인 원소의 개수를 의미한다.
이 경우 $p \rightarrow \infty$일 때 (23)의 해는 $g^*$ 에 가까워진다.
여기서 $z' = (0, \ldots, 0)$ 또는 $z' = x'$인 경우 $\pi_{x'}(z')=\infty$가 된다. 하지만 이 두 가지 경우 모두 SHAP Value의 Missingness, Local Accuracy 성질에 의하여
$$\begin{align} f_x((0, \ldots, 0)) &= f(NA, \ldots, NA) = \phi_0 = g((0, \ldots, 0)) \\ f_x(x') &= g(x') \end{align}$$
이므로 $\infty \cdot 0 = 0$으로 정의한다면 Summation 안쪽이 0이 되어 계산엔 문제가 없게 된다.
$x'$의 모든 협력체 벡터(Coalition Vector) $z'(\subset x')$의 개수는 총 $2^{|x'|}$개가 된다.
(24)의 세팅을 (23)에 적용한 해는 $\tilde{z}_i' = (z_{i1}', \ldots, z_{ip}')$를 행으로 하는 $2^{|x'|}\times p$ 설계 행렬(Design Matrix) $X$는 다음과 같고(이때 순서상 $\tilde{z}_1' = (0, 0, \ldots, 0), \tilde{z}_{2^{|x'|}}' = x'$라고 설정하자)
$$X = \begin{pmatrix} \tilde{z}_1' \\ \tilde{z}_2' \\ \vdots \\ \tilde{z}_{2^{|x'|}}' \end{pmatrix}$$
반응 변수 벡터(출력 벡터) $y = (f_x(\tilde{z}_1')-\phi_0, f_x(\tilde{z}_2')-\phi_0, \ldots, f_x(\tilde{z}_{2^{|x'|}}')-\phi_0 )$ 그리고 가중치 행렬
$$W = \begin{pmatrix} \pi_{x'}(\tilde{z}_1') & 0 & \cdots &0 \\ 0 & \pi_{x'}(\tilde{z}_2') & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \pi_{x'}(\tilde{z}_{2^{|x'|}}') \end{pmatrix}$$
인 가중 최소 제곱 선형 회귀 모형과 같다. 그리고 그 해는 다음과 같다.
$$(X^tWX)^{-1}X^tWy$$
이때 $\tilde{\phi} = (\phi_1, \ldots, \phi_p)$는 위 정리에 의하면 다음을 알 수 있다.
$$\tilde{\phi} \approx (X^tWX)^{-1}X^tWy\tag{25}$$
엇 그런데 문제가 있다.
2가지 문제가 있다.
하나는 $W_{11} = W_{2^{|x'|}, 2^{|x'|}} = \infty$라는 것이다. 실제로 구현할 때 문제가 되는데 어떤 분들은 이를 충분히 큰 값(예 : $10^7$ 등)으로 설정하여 가중 최소 제곱법을 풀기도 한다.
다른 하나는 Local Accuracy 성질이 만족하지 못하게 되는 문제가 있다. 왜냐하면 (25)로 구한 해는 SHAP Value의 근사값이기 때문이다.
따라서 이러한 문제를 해결하기 위하여 (24)를 바꿔줘야 한다. 이때 Local Accuracy를 만족하도록 다음의 제약 조건을 추가한다.
$$f(x) = c_0 +c_1+\cdots +c_p$$
또한 $\phi_0$는 학습 데이터를 이용하여 계산할 수 있으므로 $c_0 = \phi_0$로 설정한다.
다음으로 $L$을 수정해야 한다. $M = |x'|$이라할 때
$$\begin{align} L(f, g, \pi_{x'}) &= \sum_{i=1}^{2^M}\pi_{x'}(\tilde{z}_i')(f_x(\tilde{z}_i') - g(\tilde{z}_i'))^2 \\ &= \sum_{i=2}^{2^{M}-1}\pi_{x'}(\tilde{z}_i')(f_x(\tilde{z}_i') - \phi_0-c_1z_{i1}' - \cdots - c_pz_{ip}')^2 \\ &= \sum_{i=2}^{2^{M}-1}\pi_{x'}(\tilde{z}_i')(f_x(\tilde{z}_i') - \phi_0-(f(x)-\phi_0)z_{ip}' -c_1 (z_{i1}'-z_{ip}') - \\ & \cdots - c_{p-1}(z_{i, p-1}'-z_{ip}'))^2 \end{align}\tag{26}$$
먼저 $(2^M-1)\times p$행렬 $X^*$를 정의하자.
$$X^* = \begin{pmatrix} \tilde{z}_2' \\ \tilde{z}_3' \\ \vdots \\ \tilde{z}_{2^{M}-1}' \end{pmatrix}$$
그러면 (26)은 $(2^M-2)\times (p-1)$인 설계 행렬
$$X_m = \begin{pmatrix} X^*_{. , 1} - X^*_{. , p} \;\; X^*_{. , 2} - X^*_{. , p} \;; \cdots \;; X^*_{. , p-1} - X^*_{. , p} \end{pmatrix}$$
이다. 여기서 $X^*_{., j}$는 $X^*$의 $j$번째 칼럼이다.
반응 변수 벡터(출력 벡터)
$$y = \begin{pmatrix} f_x(\tilde{z}_2')-\phi_0-(f(x)-\phi_0)X^*_{1, p} \\ f_x(\tilde{z}_3')-\phi_0-(f(x)-\phi_0)X^*_{2, p} \\ \vdots \\ f_x(\tilde{z}_{2^M-1}')-\phi_0-(f(x)-\phi_0)X^*_{2^M-2, p} \end{pmatrix}$$
그리고 $(2^M-2)\times (2^M-2)$ 가중치 행렬
$$W = \begin{pmatrix} \pi_{x'}(\tilde{z}_2') & 0 & \cdots &0 \\ 0 & \pi_{x'}(\tilde{z}_3') & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & \pi_{x'}(\tilde{z}_{2^{M}-1}') \end{pmatrix}$$
인 가중 최소 제곱 선형 회귀 모형과 같다. 이때 가중치 행렬에서 무한대를 갖는 원소를 자연스럽게 제거했음을 주목하자.
따라서 (26)의 해는 $(X_m^tWX_m)^{-1}X_m^tWy$이 되고 정리에 의하여 다음과 같이 SHAP Value $\tilde{\phi} = (\phi_1, \ldots, \phi_{p-1})$를 근사하게 된다.
$$\tilde{\phi} \approx (X_m^tWX_m)^{-1}X_m^tWy\tag{27}$$
(27)을 등호로 놓고 $\phi_p = f(x) - \phi_0 - \phi_1 - \cdots - \phi_{p-1}$이 되도록 설정하면 Local Accuracy를 만족하게 된다.
좀 더 생각해볼 점이 있다.
입력 벡터에 결측이 포함된 경우를 생각해보자. 예를 들어 입력 벡터 $x = (23, NA, 10, 4)$에 대한 SHAP Value를 Kernel SHAP으로 계산한다고 해보자. 그러면 $x$의 단순화 입력 벡터 $x' = (1, 0, 1, 1)$이 되고 모든 협력체 벡터 $z'$은 총 8개로 다음과 같다.
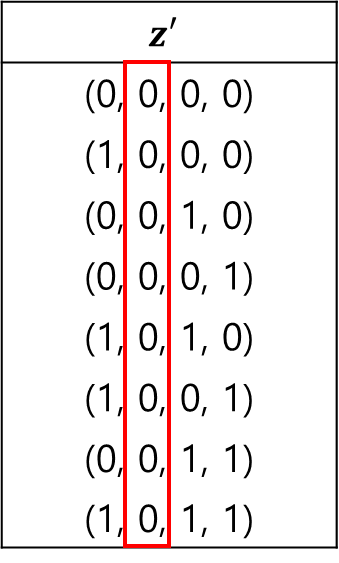
위 협력체 벡터를 이용하여 설계 행렬을 만드는 경우 2번째 칼럼($x$가 결측이 발생한 인덱스)이 모두 0이 되므로 Singular Matrix가 된다. 따라서 해당 칼럼을 지우고 $\phi_2=0$으로 설정한다. 즉, $x$의 결측이 발생한 곳의 칼럼을 모두 지우고 해당 SHAP Value를 0으로 설정한다는 것이다.
다음으로 $x$의 차원이 커지는 경우 설계 행렬의 행이 기하급수적으로 늘어난다는 것이다. 이에 따라 계산에 대한 문제가 생길 수 있다. 이때 모든 협력체 벡터에서 커널(가중치) $\pi_{x'}(z')$에 비례하여 복원 추출된 협력체 벡터만을 가지고 계산하는 방법이 있다. 예를 들어 전체 협력체 벡터에서 $D$개를 복원 추출했다고 해보자.
이때 $D \times p$ 행렬 $X^*$를 정의하자.
$$X^* = \begin{pmatrix} \tilde{z}_1' \\ \tilde{z}_2' \\ \vdots \\ \tilde{z}_{D}' \end{pmatrix}$$
이제 이를 이용하여 $X_m$, $y$, $W$를 만들어 가중 최소 제곱법으로 SHAP Value를 근사 시킨다.
b. Python 구현
이제 Kernel SHAP을 구현해보자. 여기서는 내가 구현한 것과 shap 패키지의 결과와 비교해보고자 한다.
먼저 KernelShap 클래스를 정의한다. 초기화할 때 fit을 이용하여 적합이 완료된 sklearn model 클래스를 받는다. 다음으로 $\phi_0$나 결측이 포함된 $x$에 대한 예측을 수행하기 위한 data를 넘겨줌으로써 초기화가 마무리된다.
내부 함수들을 살펴보자. 먼저 SHAP value를 계산하는 shap_values 함수를 구현하는데 이때 복원 추출 여부를 묻는 sampling 인자를 추가로 정의했다. 예측을 수행하는 predict 함수도 정의해주었다. 이때 predict 함수는 입력 벡터에 결측이 포함된 경우에도 계산할 수 있도록 구현하였다. 또한 주어진 입력 벡터에 대해서 모든 협력체 벡터로 이루어진 행렬을 만드는 generate_coalition_matrix 함수, generate_coalition_matrix 함수로 만든 행렬에 대해서 $\pi_{x'}(z')$을 계산하는 함수도 구현했다.
import pandas as pd
import numpy as np
import shap
from sklearn.datasets import load_boston
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
class KernelSHAP():
def __init__(self, model, data):
self.model = model
self.data = data
self.phi_0 = None
self.phi_ = None
def generate_coalition_matrix(self, x):
from itertools import combinations
x_simplified = np.where(pd.isna(x), 0, 1)
non_na_idx = np.where(x_simplified==1)[0]
num_features = len(non_na_idx)
coalition_matrix = [[0] * num_features]
for num_avaialable_features in range(1, num_features+1):
for comb in combinations(range(num_features), num_avaialable_features):
coalition_matrix.append([1 if i in comb else 0 for i in range(num_features)])
coalition_matrix = np.array(coalition_matrix)[1:-1]
return x_simplified, non_na_idx, coalition_matrix
def get_kernel_weights(self, mat, p):
from math import factorial
def ncr(n, r):
import operator as op
from functools import reduce
r = min(r, n-r)
numer = reduce(op.mul, range(n, n-r, -1), 1)
denom = reduce(op.mul, range(1, r+1), 1)
return numer // denom
kernel_weights = []
for row in mat:
z = np.sum(row)
p_c_z = ncr(p, int(z))
pi = (p-1)/(p_c_z*z*(p-z))
kernel_weights.append(pi)
return np.array(kernel_weights)
def shap_values(self, x, sample=None, random_state=100):
np.random.seed(random_state)
model = self.model
data = self.data
self.phi_0 = np.mean(model.predict(data))
phi_0 = self.phi_0
x_simplified, non_na_idx, coalition_matrix = self.generate_coalition_matrix(x)
X_star = np.zeros((coalition_matrix.shape[0], len(x)))
X_star[:, non_na_idx] = coalition_matrix
p = np.sum(x_simplified)
kernel_weights = self.get_kernel_weights(X_star, p)
if sample is not None:
k = int(sample*X_star.shape[0])
sampled_idx = np.random.choice(range(X_star.shape[0]), size=k, p = kernel_weights/np.sum(kernel_weights))
X_star = X_star[sampled_idx]
kernel_weights = kernel_weights[sampled_idx]
last_non_na_idx = np.max(non_na_idx)
temp_idx = sorted(set(non_na_idx) - {last_non_na_idx})
X_modified = np.column_stack([X_star[:, i]-X_star[:, last_non_na_idx] for i in temp_idx])
# predicted_val = model.predict(np.expand_dims(x, axis=0))[0] # f(x)
predicted_val = self.predict(x)
data = X
mat = X_star
# def get_original_vector_values(mat, x):
y_first_term = []
for row in mat:
z = np.array([np.nan]*len(x))
idx = np.where(row==1)[0]
z[idx] = x[idx]
data_copy = data.copy()
data_copy[:, idx] = z[idx]
temp_val = np.mean(model.predict(data_copy))
y_first_term.append(temp_val)
y_first_term = np.array(y_first_term)
y_modified = y_first_term - phi_0 -(predicted_val-phi_0)*X_star[:, last_non_na_idx]
weighted_reg = LinearRegression().fit(X_modified, y_modified, sample_weight=kernel_weights)
phi_ = []
na_idx = set(range(len(x))) -set(non_na_idx)
coef_idx = 0
for i in range(len(x)-1):
if i in na_idx:
phi_.append(0)
else:
phi_.append(weighted_reg.coef_[coef_idx])
coef_idx += 1
last_phi = predicted_val - phi_0 - np.sum(phi_)
phi_.append(last_phi)
self.phi_ = phi_
return self.phi_0, self.phi_
def predict(self, x):
data = self.data.copy()
if len(np.where(pd.isna(x))[0]) == 0:
x = np.expand_dims(x, axis=0)
return self.model.predict(x)[0]
else:
idx = np.where(~pd.isna(x))[0]
data[:, idx] = x[idx]
return np.mean(self.model.predict(data))
이번엔 보스턴 집값 데이터를 이용하여 SHAP Value를 계산하고자 한다.
데이터를 만들고 이를 이용하여 예측 모형을 학습한다. 여기선 랜덤 포레스트를 사용했다. 그리고 $\phi_0$나 결측이 포함된 $x$에 대한 예측을 수행하기 위해 학습 데이터를 사용했다.
## 보스턴 데이터
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['MEDV'] = boston.target
X = df[['AGE', 'RAD', 'TAX', 'DIS', 'RM', 'LSTAT', 'B', 'INDUS', 'CHAS']].values
y = df['MEDV'].values
## 예측 모형 모형 적합
model = RandomForestRegressor(max_depth=4,
random_state=0,
n_estimators=20).fit(X, y)
## 결측 처리를 위한 데이터 샘플
data = X
## KernelSHAP 클래스 초기화
kernel_shap = KernelSHAP(model, data)
- 결측값이 포함되지 않은 경우 -
이제 SHAP Value를 계산하고 개별 예측값과 SHAP Value의 합과 일치하는지 살펴보자.
explain_vector = X[0].copy()
kernel_shap.shap_values(explain_vector)
print('Expected Values :', kernel_shap.phi_0)
print('Shap Values :', kernel_shap.phi_)
print('Prediction Value :', kernel_shap.predict(explain_vector))
print('Sum Phi :', kernel_shap.phi_0+np.sum(kernel_shap.phi_))

이번엔 sampling 인자를 설정하여 결과를 살펴보았다.
kernel_shap.shap_values(explain_vector, sample=0.5)
print('Expected Values :', kernel_shap.phi_0)
print('Shap Values :', kernel_shap.phi_)
print('Prediction Value :', kernel_shap.predict(explain_vector))
print('Sum Phi :', kernel_shap.phi_0+np.sum(kernel_shap.phi_))

기존 SHAP Value와는 차이가 있었다. 심지어 부호가 바뀌는 경우도 있었다.
이번엔 shap 패키지를 이용하여 Kernel SHAP Value를 계산해보자. 여기서는 KernelExplainer를 사용하는데 기존과는 다르게 predict 함수를 첫 번째 인자로 넣어야 한다.
explainer = shap.KernelExplainer(model.predict, data)
k_shap_values = explainer.shap_values(explain_vector)
print('Expected Values :', explainer.expected_value)
print('Shap Values :', k_shap_values)
print('Sum Phi :', explainer.expected_value+np.sum(k_shap_values))

첫 번째 결과와 동일하게 출력되었다.
- 결측값이 포함된 경우 -
이번엔 의도적으로 첫 번째, 세 번째 값을 결측으로 바꾸고 SHAP Value를 계산해보았다.
explain_vector = X[0].copy()
explain_vector[0] = np.nan
explain_vector[3] = np.nan
kernel_shap.shap_values(explain_vector)
print('Expected Values :', kernel_shap.phi_0)
print('Shap Values :', kernel_shap.phi_)
print('Prediction Value :', kernel_shap.predict(explain_vector))
print('Sum Phi :', kernel_shap.phi_0+np.sum(kernel_shap.phi_))

이번엔 복원 추출을 이용한 SHAP Value를 구해보았다.
kernel_shap.shap_values(explain_vector, sample=0.5)
print('Expected Values :', kernel_shap.phi_0)
print('Shap Values :', kernel_shap.phi_)
print('Prediction Value :', kernel_shap.predict(explain_vector))
print('Sum Phi :', kernel_shap.phi_0+np.sum(kernel_shap.phi_))

이번엔 shap 패키지에서는 입력 벡터에 결측이 있으면 에러가 발생한다.
explainer = shap.KernelExplainer(model.predict, data)
k_shap_values = explainer.shap_values(explain_vector)
print('Expected Values :', explainer.expected_value)
print('Shap Values :', k_shap_values)
print('Sum Phi :', explainer.expected_value+np.sum(k_shap_values))
그래서 KernelExplainer이 아닌 앞에서 사용한 Explainer를 가지고 계산해보았다.
explainer = shap.Explainer(model, data)
shap_values = explainer.shap_values(explain_vector)
print('Expected Values :', explainer.expected_value)
print('Shap Values :', shap_values)
print('Sum Phi :', explainer.expected_value+np.sum(shap_values))

뭔가 나오긴 하는데 합이 맞지 않았다. 원래는 27.1이 나와줘야 하는데 보는 바와 같이 45가 넘는 값이 나왔다. ㄷㄷ;; 좀 이상하다.
또한 data 인자를 학습 데이터(X) 전체로 하는 경우에 대해서는 내가 구현한 것과 shap 패키지의 결과가 일치하였지만 학습 데이터에서 샘플링된 데이터로 한 경우에 대해서는 약간 차이가 났다. 내부 동작 과정에서 뭔가 다른 것 같은데 정확한 원인을 찾지 못했다.
4) Tree SHAP
a. 정의
만약 랜덤 포레스트나 기본 학습기를 의사결정나무(Decision Tree)를 사용하는 앙상블 모형의 경우 이러한 나무 구조를 이용하여 좀 더 쉽게 SHAP Value를 구할 수 있도록 개발된 것이 Tree SHAP이다.
Tree SHAP은 Exact SHAP, Kernel SHAP과는 달리 별도의 데이터 없이 $f_S(x_S)$를 계산할 수 있다. 그 방법을 예를 들어 소개한다.
원리는 랜덤 포레스트나 나무 기반 앙상블 모형에 모두 적용할 수 있으므로 먼저 설명의 편의를 위해 학습된 의사결정나무가 하나 있다고 하겠다.

이때 $x = (8, 10, NA, 7)$인 경우 $f_S(x_S)$를 구해보자. 첫 번째, 두 번째, 네 번째 변수가 결측이 아니므로 $$S = \{1, 2, 4 \}$$
가 된다.
주어진 $x$에 대하여 나무를 따라가 보자.

빨간색 화살표를 따라가 보면 빨간 박스에서 막히게 된다. 왜냐하면 $x_3 = NA$이기 때문이다. 이때 Tree SHAP은 해당 노드의 자식 노드(파랑 박스)를 샘플 비율에 따른 예측값의 가중 평균을 $f_S(x_S)$ 고려하게 된다.
$$f_S(x_S) = \frac{10}{80}\cdot 27 + \frac{70}{80}\cdot 39 = 37.5$$
이번엔 결측값이 두 개인 $x = (1, NA, NA, 7)$인 경우에 대해서 $f_S(x_S)$를 구해보자. 이번에도 의사결정나무를 잘 따라가다 보면 $x_2= NA$이므로 위에서 첫 번째 빨간 박스($\text{Node}$)에서 막히게 된다.

이때에는 자식 노드들의 샘플 비율에 따른 가중 평균 예측치를 계산해야 한다.
$$f_S(x_S) = \frac{25}{80}\cdot\text{Prediction Value of}\;\; \text{Node}_\text{left} + \frac{55}{80} \cdot \text{Prediction Value of}\;\; \text{Node}_\text{right}$$
이때 $\text{Node}_\text{left}$에서 또 막히는데 $x_3=NA$이기 때문이다. 따라서 앞의 예제에서 살펴본 계산 방식을 쓰면 다음과 같다.
$$\text{Prediction Value of}\;\; \text{Node}_\text{left} = \frac{10}{25}\cdot 15+\frac{15}{25}\cdot 28$$
반면 $x_4=7$이므로 맨 아래 파란 박스로 따라가면 예측값을 얻을 수 있다.
$$\text{Prediction Value of}\;\; \text{Node}_\text{right} = 12 $$
이를 종합하면
$$ f_S(x_S) = \frac{25}{80}\cdot \left ( \frac{10}{25}\cdot 15+\frac{15}{25}\cdot 28\right )+ \frac{55}{80} \cdot 12 = 15.375$$
$f_S(x_S)$를 계산할 때 특별한 데이터 셋을 사용하지 않았다는 점을 주목하자.
그리고 의사결정나무의 마디(노드)만 따라가면 되므로 계산 속도가 나무 깊이에 비례한다. 일반적으로 나무 깊이는 $f_S(x_S)$를 계산하기 위해 필요한 데이터 셋의 크기보다 작다. 따라서 계산 속도가 데이터 셋의 크기에 비례하는 Exact SHAP보다 Tree SHAP의 SHAP Value 계산 속도가 더 빠르다.
b. Python 구현
위 내용을 바탕으로 Tree SHAP을 구현해보자.
먼저 TreeSHAP 클래스를 정의한다. TreeSHAP은 ExactShap에서 get_f_s 함수를 바꾸고 data 인자를 쓰는 부분을 바꿔준 것 외에는 구조가 동일하다.
class TreeShap():
def __init__(self, model):
self.model = model
self.phi_0 = None
self.phi_ = None
def powerset(self, l):
x = len(l)
res = []
for i in range(1 << x):
temp = [l[j] for j in range(x) if (i & (1 << j))]
res.append(temp)
return res
def get_f_s(self, model, x, s):
def pv(node, w): ## get predicted value
left_child = model.tree_.children_left[node]
right_child = model.tree_.children_right[node]
if left_child == right_child: # node is a leaf
return w*model.tree_.value[node].squeeze()
else: # internal node
feature = model.tree_.feature[node]
if feature in s:
if x[feature] <= model.tree_.threshold[node]:
return pv(left_child, w)
else:
return pv(right_child, w)
else:
w_left = model.tree_.n_node_samples[left_child] / model.tree_.n_node_samples[node]
w_right = model.tree_.n_node_samples[right_child] / model.tree_.n_node_samples[node]
return pv(left_child, w * w_left) + pv(right_child, w * w_right)
return pv(0,1)
def shap_values(self, x):
model = self.model
self.phi_0 = self.get_f_s(model, x, [])
phi_ = []
missing_idx_set = set(np.where(pd.isna(x))[0])
for i, val in enumerate(x):
if pd.isna(val):
phi_.append(0)
else:
p = data.shape[1]
target_set = set(range(p))-{i}
if missing_idx_set:
target_set = target_set - missing_idx_set
p = p-len(missing_idx_set)
target_set = list(target_set)
all_subset = self.powerset(target_set)
temp_phi = 0
for s in all_subset:
temp_val = self.get_f_s(model, x, s+[i]) - self.get_f_s(model, x, s)
temp_val = factorial(len(s))*factorial(p-len(s)-1)/factorial(p)*temp_val
temp_phi += temp_val
phi_.append(temp_phi)
self.phi_ = phi_
return (self.phi_0, self.phi_)
def predict(self, x):
model = self.model
if len(np.where(pd.isna(x))[0]) == 0:
x = np.expand_dims(x, axis=0)
return self.model.predict(x)[0]
else:
idx = np.where(~pd.isna(x))[0]
return self.get_f_s(model, x, idx)
이번에도 보스턴 집값 데이터를 이용한다. 예측 모형으로는 의사결정나무를 사용했다. 그러고 나서 TreeSHAP 인스턴스를 생성해주었다.
## 보스턴 데이터
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['MEDV'] = boston.target
X = df[['AGE', 'RAD', 'TAX', 'DIS', 'RM', 'LSTAT', 'B', 'INDUS', 'CHAS']].values
y = df['MEDV'].values
## 예측 모형 모형 적합
model = DecisionTreeRegressor(max_depth=4, random_state=0).fit(X, y)
## TreeSHAP 클래스 초기화
tree_shap = TreeShap(model)
- 결측값이 포함되지 않은 경우 -
구현을 했으니 테스트를 해봐야 한다. SHAP Value를 계산하고 개별 예측값과 SHAP Value의 합과 일치하는지 살펴보자.
explain_vector = X[0].copy()
tree_shap.shap_values(explain_vector)
print('Expected Values :', tree_shap.phi_0)
print('Shap Values :', tree_shap.phi_)
print('Prediction Value :', tree_shap.predict(explain_vector))
print('Sum Phi :', tree_shap.phi_0+np.sum(tree_shap.phi_))

개별 예측값과 SHAP Value 합이 일치했다. 아직은 안심하기 이르다. shap 패키지와 동일한 결과가 나와줘야 한다. shap에서는 TreeExplainer를 통해서 Tree SHAP Value를 계산할 수 있다.
explainer = shap.TreeExplainer(model)
tree_shap_values = explainer.shap_values(explain_vector)
print('Expected Values :', explainer.expected_value[0])
print('Shap Values :', tree_shap_values)
print('Prediction Value :', tree_shap.predict(explain_vector))
print('Sum Phi :', explainer.expected_value[0]+np.sum(tree_shap_values))

내가 구현한 것과 결과가 똑같이 나왔다. 짝짝~!!
근데 이상한 것은 1, 8, 9번째 변수가 결측이 아닌데도 SHAP Value는 0이 나왔다. 이상해서 나무를 그려보았다.
import matplotlib.pyplot as plt
from sklearn.tree import plot_tree
print(explain_vector)
## [ 65.2 1. 296. 4.09 6.575 4.98 396.9 2.31 0. ]
fig = plt.figure(figsize=(25, 10))
fig.set_facecolor('white')
plot_tree(model, fontsize =16)
plt.show()

주어진 입력 벡터에 따라서 가보면 예측에 사용된 변수는 4, 5, 6번째 변수이고 1, 8, 9번째 변수는 안 쓰였으므로 1, 8, 9번째 변수에 해당하는 SHAP Value는 0이 나오는 것이 상식적이다.
하지만 이를 제외한 2, 3, 7번째 변수는 사용되지 않았음에도 불구하고 해당 SHAP Value가 0이 아니다. 이는 기여도 계산을 위한 두 값의 차이 $f_{S\cup \{i\}}(x_{S\cup \{i\}}) - f_{S}(x_S)$를 계산할 때 Exact SHAP(또는 Linear SHAP)의 경우 두 값을 같은 데이터 셋을 사용하여 계산하지만 Tree SHAP 그렇지 않기 때문이다.
즉, Tree SHAP은 Missingness를 만족하지 않는다는 것이다.
- 결측값이 포함된 경우 -
이번엔 의도적으로 결측값을 포함시키고 SHAP Value를 계산해보았다.
explain_vector = X[0].copy()
explain_vector[5] = np.nan
explain_vector[6] = np.nan
tree_shap.shap_values(explain_vector)
print('Expected Values :', tree_shap.phi_0)
print('Shap Values :', tree_shap.phi_)
print('Prediction Value :', tree_shap.predict(explain_vector))
print('Sum Phi :', tree_shap.phi_0+np.sum(tree_shap.phi_))

문제없이 잘 나왔다. 이때 6, 7 번째 변수는 결측이므로 해당 SHAP Value가 0으로 잘 나왔다. 이번엔 shap 패키지를 사용해보자.
explainer = shap.TreeExplainer(model)
tree_shap_values = explainer.shap_values(explain_vector)
print('Expected Values :', explainer.expected_value[0])
print('Shap Values :', tree_shap_values)
print('Prediction Value :', tree_shap.predict(explain_vector))
print('Sum Phi :', explainer.expected_value[0]+np.sum(tree_shap_values))

Kernel SHAP과 마찬가지로 shap 패키지는 결측이 포함된 입력 벡터에 대해서 예측값과 SHAP Value의 합이 일치하지 않는다. shap 패키지는 결측을 잘 처리 못하는 건가 싶다.
4. 장단점
- 장점 -
a. SHAP Value의 합리적인 성질 덕분에 개별 예측값에 대한 각 변수의 중요도를 상식적으로 제공한다.
b. Model Agnostic 한 방법이다.
SHAP은 예측 모형 클래스의 관계없이 적용할 수 있어서 유연하다.
c. 특정 모형 클래스에 대해서는 계산이 빠르다.
Model Agnostic이지만 예측 모형이 선형인 경우에는 공식이 있어서 SHAP Value를 굉장히 빠르게 계산할 수 있고 Tree 기반의 모형 또한 Tree의 구조를 사용하여 빠른 계산 속도를 보여준다.
d. 개별 예측값(Local)에 대한 변수 중요도뿐만 아니라 예측에 대한 전반적인 변수 중요도도 계산할 수 있다.
- 단점 -
a. Kernel SHAP은 계산이 느리다.
예측하고자 할 입력 벡터들이 많으면 계산 속도가 느려서 실용적이지 못하다고 한다.
b. Tree SHAP은 Missingness를 만족하지 않아서 때때로 해석이 직관적이지 않다.
특정 변수의 SHAP Value가 0이 아니지만 실제로 개별 예측값 계산 시 사용되지 않는 경우가 있다. 이 경우 SHAP Value의 해석이 직관적이지 않다.
요즘 회사에서 SHAP이 핫하다길래 한번 공부해봤다. 게임 이론에서 가져온 Shapley Value를 이용했다는 것이 신선했고 꽤나 쓸모 있어 보였다. 하지만 Lundberg, Su-In Lee의 원 논문만을 읽고 이해하기는 불가능했다(내가 머리가 나빠서 그런 듯하다). 그래서 여러 자료 찾아보고 공부하느라 애를 좀 먹었다. 그래도 SHAP Value를 심간에 새기는 계기가 되어 뿌듯했다.

- 참고자료 -
Introduction to SHAP Values and Their Application in Machine Learning
Shapley Value wiki - https://en.wikipedia.org/wiki/Shapley_value
SHAP - https://christophm.github.io/interpretable-ml-book/shap.html
'통계 > 머신러닝' 카테고리의 다른 글
| 27. Partial Dependence Plot (부분 의존도 그림), Individual Conditional Expectation Plot (개별 조건부 평균 그림)에 대해서 알아보자 with Python (0) | 2022.09.02 |
|---|---|
| 26. 변수 중요도(Variable Importance) with Python (0) | 2022.08.27 |
| 24. 랜덤 포레스트(Random Forest)에 대해서 알아보자 (3) | 2022.08.05 |
| 23. 배깅(Bagging)에 대해서 알아보자 (0) | 2022.07.20 |
| 22. 로지스틱 회귀(Logistic Regression)에 대해서 알아보자. (364) | 2022.07.03 |





댓글