이번 포스팅에서는 기존 최소 제곱법을 이용하여 시계열 데이터를 분석하는 방법과 파이썬(Python)으로 구현하는 방법에 대해서 알아보고자 한다.
여기서 다루는 내용은 다음과 같다.
1. 선형 추세 분석
시계열 데이터 $(Y_t : t=1, \ldots, n)$가 주어졌다고 하자. 이때 $y_t$에 대하여 다음과 같은 가정을 해보자. $$Y_t = \mu_t + X_t$$
여기서 $\mu_t$는 Deterministic Trend(시간 $t$에 대한 함수라고 생각하자)이고 $X_t$는 평균이 0이고 분산이 $\sigma^2$인 IID(Indepedent and Indentical Distributed) Process이다.
- 추정 방법 -
시계열 데이터에 선형 추세만 존재한다고 판단될 경우 $\mu_t = b_0 + b_1t$라 가정하고 최소 제곱법을 이용하여 $b_0와 b_1$을 추정한다. 즉, 다음과 같이 $Q$를 최소화하는 $b_0, b_1$을 찾는다.
$$Q(b_0, b_1) = \sum_{t=1}^N(Y_t - b_0 - b_1t)^2$$
미분을 이용하면 $Q$를 최소화하는 값은 아래와 같다.
$$\hat{b}_0 = \bar{Y} - \hat{b}_1\bar{t}, \;\;\; \hat{b}_1=\frac{\sum_{t=1}^n(Y_t-\bar{Y})(t-\bar{t})}{\sum_{t=1}^n(t-\bar{t})^2}$$
여기서 $\bar{Y} = \sum_{t=1}^nY_t/n, \;\; \bar{t} = (n+1)/2$이다.
- 예측 방법 -
시계열 데이터 분석에서는 미래 시점에 대한 예측값을 추정하는 것에 매우 큰 관심이 있다. $n+l$ 시점에서 예측값 $\hat{Y}_{n+l}$은 다음과 같다.
$$\hat{Y}_{n+l} = \hat{b}_0+\hat{b}_1(n+l)$$
$$X =
\begin{pmatrix}
1 & 1 \\
1 & 2 \\
\vdots & \vdots \\
1 & t
\end{pmatrix}, x_{n+l} = (1, n+l)^t$$
이고 $X_t$가 추가적으로 정규분포를 따른다고 가정하자. 예측값에 대한 (1-$\alpha$)% 예측 구간은 다음과 같이 구한다.
$$\hat{Y}_{n+l} \pm t_{\alpha/2}(n-2)s\sqrt{1+x_{n+l}^t(X^tX)^{-1}x_{n+l}}$$
여기서 $t_{\alpha/2}(n-2)$는 자유도가 $n-2$인 $t$분포에서 오른쪽 꼬리값이 $\alpha/2$가 되게 하는 값이고
$$s^2 = \frac{\sum_{t=1}^n(Y_t-\hat{b}_0-\hat{b}_1t)^2}{n-2}$$
이다.
- 실제 데이터 분석 -
이번엔 실제 데이터를 이용해서 선형 추세를 모델링해보자. 먼저 데이터를 다운받자. 이 데이터는 1980년부터 2015년까지 오스트레일리아 방문자 수를 나타낸 것이다.
필요한 모듈을 임포트한다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from scipy.stats import t
데이터를 불러온다.
df = pd.read_csv('./dataset/australia_visitor.csv')
데이터를 보면 알겠지만 날짜 정보가 포함되어있지 않다. 시계열 데이터를 분석할 때에는 날짜 정보가 추가되어야 시각화할 때도 좋다. 따라서 아래와 같이 날짜를 추가해줘야 한다. date_range 사용 예제는 여기를 참고하자.
start_date = '1980-01-01'
end_date = '2015-12-31'
df.index = pd.date_range(start_date,end_date,freq='y')
날짜가 잘 추가된 것을 확인할 수 있다.
데이터가 어떤 모양인지 확인해보기 위하여 시각화해보자.
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.plot(df['visitors'],marker='o',markerfacecolor='none')
plt.ylabel('Number of Visitors (millons)')
plt.xlabel('Time (year)')
plt.show()
증가하는 추세가 뚜렷해보인다.
이제 선형 모형을 적합시켜보자. 먼저 기존의 선형 회귀 모형을 적합할 때처럼 종속변수 $y$와 설명변수로 이루어진 행렬 $X$를 정해준다. $X$에 1로 이루어진 열 벡터를 추가하는 것을 잊지 말자.
df['time'] = range(1,len(df)+1) ## time 변수 생성
y = df['visitors']
X = df['time']
X = sm.add_constant(X)
이제 파라미터들을 추정한다.
time = df['time']
mean_t = time.mean()
mean_y = y.mean()
b1 = np.sum((y-mean_y)*(time-mean_t))/np.sum(np.square(time-mean_t))
b0 = mean_y-b1*mean_t
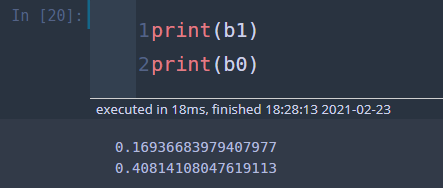
위 값은 statsmodels의 OLS를 이용하여 구할 수도 있다.
ols_fit = sm.OLS(y,X).fit()
b1 = ols_fit.params.time
b0 = ols_fit.params.const
이제 예측값과 예측구간을 구해본다. 난 향후 5년까지의 예측값과 95% 예측 구간을 구할 것이다.
future = [1,2,3,4,5]
n = len(df)
alpha = 0.05
X_tX_inv = np.linalg.inv(X.T.dot(X))
t_val = t.ppf(1-alpha/2,df=n-2)
predict_vals = []
upper_limit = []
lower_limit = []
for l in future:
predict_val = b0+b1*(n+l)
s2 = np.sum(np.square(y-b0-b1*time))/(n-2)
x = np.array([[1],[n+l]])
variance_factor = np.sqrt(1+x.T.dot(X_tX_inv.dot(x)))
limit = t_val*np.sqrt(s2)*variance_factor[0][0]
predict_vals.append(predict_val)
upper_limit.append(predict_val+limit)
lower_limit.append(predict_val-limit)
결과를 시각화해보자. 이를 위해서는 5년까지에 대응하는 날짜를 만들어줘야 한다.
start_date = '2016-01-01'
pred_data = {
'pred':predict_vals,
'ul':upper_limit,
'll':lower_limit
}
pred_df = pd.DataFrame(pred_data)
pred_df.index = pd.date_range(start_date,periods=future[-1],freq='Y')
fitted_val = b0+b1*time
vals = pd.concat([fitted_val,pred_df['pred']])
다음은 시각화 코드이다. fill_between을 사용하여 예측 구간 사이에 영역을 옅은 파란색으로 채웠다.
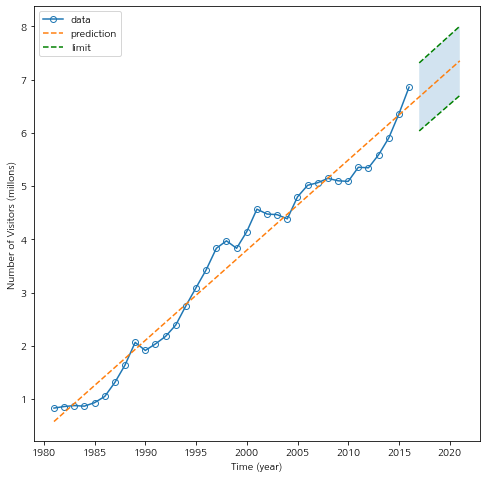
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
marker_config = dict()
marker_config['marker'] = 'o'
marker_config['markerfacecolor'] = 'none'
plt.plot(df['visitors'],label='data',**marker_config)
plt.plot(vals,label='prediction',linestyle='--')
plt.plot(pred_df['ll'],color='green',linestyle='--',label='limit')
plt.plot(pred_df['ul'],color='green',linestyle='--')
plt.fill_between(pred_df.index,pred_df['ll'],pred_df['ul'],alpha=0.2)
plt.legend(loc='upper left')
plt.ylabel('Number of Visitors (millons)')
plt.xlabel('Time (year)')
plt.show()
위 코드를 실행하면 아래와 같이 예측값과 예측 구간을 예쁘게 시각화할 수 있다.
2. 계절성을 가진 데이터 분석
이번엔 시계열 데이터에 계절성 패턴만 보인다고 했을 때 모형을 어떻게 적합하는지에 대하여 알아보자. 먼저 시계열 데이터 $(Y_t : t=1, \ldots, n)$에서 주기가 $s$인 계절성을 보인다고 하자. 예를 들어 데이터는 월 단위로 이루어져 있고 1년 주기의 계절성이 보인다고 한다면 $s=12$가 된다.
모형 적합 방법은 더미 변수를 이용한 방법과 삼각함수를 이용한 방법이 있다.
1) 더미 변수를 이용한 방법
- 추정 방법 -
시계열 데이터 $(Y_t : t=1, \ldots, n)$를 다음과 같이 모델링할 수 있다.
$$\mu_t = b_0 + b_1 + \cdots + b_{s-1}$$
여기서 $b_j = I(t = j (\text{mod } s)), \;j=0, 1, \ldots, s-1$이다. 즉, 계절성 패턴만 보이는 시계열 데이터의 경우 더미 변수를 이용하여 모델링할 수 있는 것이다. 참고로 나는 마지막 주기에 대한 파라미터 $b_s$를 제외하였다. 이에 제외하는 모수에 따라서 추정값이 달라질 수 있지만 적합값에는 변화가 없다.
각 모수는 최소 제곱법을 이용하여 추정할 수 있다. 먼저 $b = (b_0, b_1, \ldots, b_{s-1})$, $y=(Y_1, Y_2, \ldots, Y_n)$ 그리고 $n \times s$ 행렬 $X$의 $t$번째 행을 $x_t$라 하자. 또한 $j$를 아래 식을 만족한다고 하자.
$$t = j \;\;(\text{mod } s)$$
이때 앞서 가정한 모형으로 인하여 $x_t$의 첫 번째 원소와 $j$번째 원소는 1이고 나머지는 0이다. 따라서 최소 제곱 추정량 $\hat{b}$는 다음과 같이 구할 수 있다.
$$\hat{b} = (X^tX)^{-1}X^ty$$
- 예측 방법 -
시점 $t'$에 대해서 $Y_{t'}$의 예측값 $\hat{Y}_{t'}$은 다음과 같이 계산한다.
$$\hat{Y}_{t'} = \begin{cases} \hat{b}_0, & \text{if } t' = 0\;\;(\text{mod }s) \\ \hat{b}_0+\hat{b}_j, & \text{if } t' = j(\neq 0) \;\;(\text{mod }s)\end{cases}$$
($1-\alpha$)% 예측구간은 다음과 같이 구할 수 있다.
$$\hat{Y}_{t'} \pm t_{\alpha/2}(n-s)\hat{\sigma}\sqrt{1+\tilde{x}_j^t(X^tX)^{-1}\tilde{x}_j}$$
여기서 $t_{\alpha/2}(n-s)$는 자유도가 $n-s$인 $t$분포에서 오른쪽 꼬리값이 $\alpha/2$가 되게 하는 값이고 $\hat{\sigma}^2 = \sum_{t=1}^n(y_t-x_t^t\hat{b})^2/(n-s)$이며 $\tilde{x}_j$는 첫 번째 원소와 $j$번째 원소가 1이고 나머지는 0이며 길이가 $s$인 벡터이다(아래 첨자 $t$는 시간을 나타내며 위 첨자 $t$는 Transpose를 나타낸 것이며 $t = j \;\;\text{mod } s$이다).
- 장단점 -
더미 변수를 사용하는 방법은 해석이 좋다는 장점이 있지만 주기가 커질 경우, 즉 $s$가 커질 경우 추정해야 할 파라미터의 개수가 많아져 추정된 모형이 불안정할 수 있다.
2) 삼각함수를 이용한 방법
이번엔 삼각함수를 이용하여 계절성만을 갖는 시계열 데이터를 모델링하는 방법에 대해서 알아보자.
- 추정 방법 -
삼각함수를 이용하는 방법은 $\mu_t$를 다음과 같다고 가정하는 것에서 출발한다.
$$\mu_t = b_0+b\cos \left(\frac{2\pi t}{s}+\phi\right)\tag{1}$$
여기서 추정해야 할 파라미터는 $b$와 $\phi$이다. 하지만 식 (1)은 파라미터에 대해서 선형이 아니므로 적절하게 변형해줘야 한다. 삼각함수에 덧셈 정리를 이용하여 식 (1)을 변형해보자.
$$\begin{align}b\cos \left(\frac{2\pi t}{s}+\phi\right) &= b\left\{\cos \left(\frac{2\pi t}{s}\right)\cos \phi - \sin \left(\frac{2\pi t}{s}\right)\sin \phi\right\} \\ &= b_1\cos \left(\frac{2\pi t}{s}\right) + b_2 \sin \left(\frac{2\pi t}{s}\right)\end{align}$$
여기서 $b_1 = b\cos \phi, b_2 = -b \sin \phi$ 이다. 이제 추정해야 할 파라미터는 $b_1, b_2$이며 파라미터에 대하여 선형 식이 완성되었다. 참고로 $b_1, b_2$를 이용하여 식 (1)로 바꾸고 싶다면 $ b = \sqrt{b_1^2+b_2^2}$, $\phi = \tan ^{-1}(-b_2/b_1)$를 이용하자.
$n\times 3$ 행렬 $X$를 다음과 같이 설정하자.
$$X =
\begin{pmatrix}
1 & \sin \left(\frac{2\pi\cdot 1}{s}\right) & \cos \left(\frac{2\pi\cdot 1}{s}\right)\\
1 & \sin \left(\frac{2\pi\cdot 2}{s}\right) & \cos\left(\frac{2\pi\cdot 2}{s}\right)\\
\vdots & \vdots & \vdots \\
1 & \sin \left(\frac{2\pi\cdot n}{s}\right) & \cos\left(\frac{2\pi\cdot n}{s}\right)
\end{pmatrix}$$
여기서 $\mathbf{b} = (b_0, b_1, b_2)$, y = (Y_1, \ldots, Y_t) 최소 제곱 추정량 $\hat{\mathbf{b}}$는 다음과 같다.
$$\mathbf{b} = (X^tX)^{-1}X^ty$$
- 예측 방법 -
시점 $t'$에 대한 예측값 $\hat{Y}_{t'}$은 다음과 같이 구할 수 있다.
$$\hat{Y}_{t'} = x^t\mathbf{b}$$
여기서 $x = (1, \sin (2\pi t'/s), \cos (2\pi t'/s))^t$이다.
($1-\alpha$)% 예측구간은 다음과 같이 구할 수 있다.
$$\hat{Y}_{t'} \pm t_{\alpha/2}(n-s)\hat{\sigma}\sqrt{1+x^t(X^tX)^{-1}x}$$
- 장단점 -
앞서 살펴보았던 더미 변수를 사용하는 방법에 비해서 추정해야 할 파라미터의 수가 적다는 장점이 있다. 따라서 최종 모형이 안정적(stable)이다. 하지만 설명 변수에 삼각함수가 포함되어있어 모형의 해석이 어렵다는 단점이 있다.
3) 실제 데이터 분석
먼저 여기에서 사용할 데이터를 다운받자. 미국 아이오와주 더뷰크(Dubuque) 도시의 1964년 1월부터 1975년 12월까지 온도를 나타내는 데이터이다.
필요한 모듈을 임포트하고 데이터를 불러온다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
from scipy.stats import tdf = pd.read_csv('./dataset/dubuque_temperature.csv')
데이터를 보면 날짜 정보가 포함 안되어 있다.
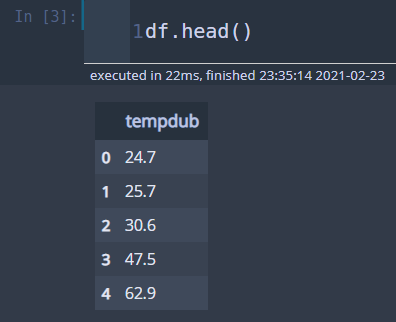
따라서 날짜를 인덱스로 넣어준다.
start_date = pd.to_datetime('1964-01-01')
end_date = pd.to_datetime('1975-12-31')
df.index = pd.date_range(start_date,end_date,freq='m')
인덱스에 날짜가 잘 들어갔다.
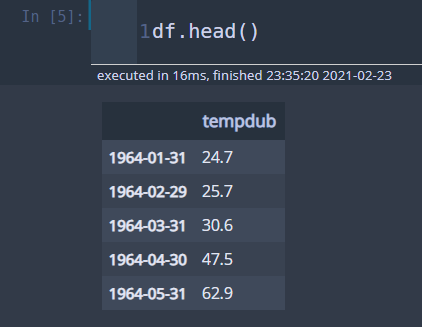
데이터가 어떤 모양을 갖고 있는지 시각화해보자.
fig = plt.figure(figsize=(8,4))
fig.set_facecolor('white')
plt.plot(df['tempdub'],marker='o',markerfacecolor='none')
plt.show()
계절성 패턴을 따르는 데이터의 표본이라 할 수 있다. 이제 앞서 살펴본 2가지 방법을 이용하여 모델링해보자. 먼저 더미 변수를 사용하여 모형을 만들어보자.
- 더미 변수를 사용한 모델링 -
난 time이라는 열을 만들고 1월부터 11월에 해당하는 더미 변수를 만들었다(선형 종속 문제로 인하여 12월은 제외하였다). 그리고 선형 회귀 모형에서처럼 종속 변수와 설명 변수 행렬을 지정해주었다. 설명 변수 행렬에는 1로 이루어진 열을 추가해줘야 한다.
df['time'] = range(1,len(df)+1) ## time 변수 생성
y = df['tempdub']
season = ['Jan', 'Feb', 'Mar', 'Apr', 'May', 'Jun',
'Jul', 'Aug', 'Set', 'Oct', 'Nov']
temp_data = dict()
period = 12
for i, s in enumerate(season):
temp = []
for time in df['time']:
if time%period == i+1:
temp_val = 1
else:
temp_val = 0
temp.append(temp_val)
temp_data[s] = temp
temp_df = pd.DataFrame(temp_data)
temp_df.index = pd.date_range(start_date,end_date,freq='m')
X = temp_df
X = sm.add_constant(X)
이제 파라미터를 추정한다. 추가적으로 1964년 1월부터 1975년 12월까지의 적합값도 추정하였다.
X_tX_inv = np.linalg.inv(X.T.dot(X))
bs = X_tX_inv.dot(X.T.dot(y.values)) ## estimated parameters
fitted_val = X.dot(bs) ## fitted values
다음으로 1976년 1월부터 12월까지의 예측값과 예측구간을 구해보자.
future = list(range(1,13))
n = len(df)
alpha = 0.05
t_val = t.ppf(1-alpha/2,df=n-len(bs))
predict_vals = []
upper_limit = []
lower_limit = []
s2 = np.sum(np.square(y-fitted_val))/(n-len(bs))
for l in future:
if l%period == 0:
predict_val = bs[0]
else:
predict_val = bs[l%period]+bs[0]
x = np.zeros(period)
x[0] = 1
if l%period != 0:
x[l%period] = 1
x = np.expand_dims(x,axis=1)
variance_factor = np.sqrt(1+x.T.dot(X_tX_inv.dot(x)))
limit = t_val*np.sqrt(s2)*variance_factor[0][0]
predict_vals.append(predict_val)
upper_limit.append(predict_val+limit)
lower_limit.append(predict_val-limit)
시각화를 위해 1976년 1월부터 12월에 해당하는 날짜를 인덱스로 하는 데이터 프레임을 만들었고 추가적으로 예측값과 적합값을 하나로 합쳤다.
strt_date = '1976-01-01'
pred_data = {
'pred':predict_vals,
'ul':upper_limit,
'll':lower_limit
}
pred_df = pd.DataFrame(pred_data)
pred_df.index = pd.date_range(strt_date,periods=future[-1],freq='m')
vals = pd.concat([fitted_val,pred_df['pred']])
이제 결과를 시각화해보자. 아래는 시각화 코드이다.
fig = plt.figure(figsize=(10,5))
fig.set_facecolor('white')
marker_config = dict()
marker_config['marker'] = 'o'
marker_config['markerfacecolor'] = 'none'
plt.plot(df['tempdub'],label='data',**marker_config)
plt.plot(vals,label='prediction',linestyle='--')
lineconfig = dict()
lineconfig['linestyle'] = '--'
lineconfig['linewidth'] = 1
plt.plot(pred_df['ll'],color='green',**lineconfig,label='limit')
plt.plot(pred_df['ul'],color='green',**lineconfig)
plt.fill_between(pred_df.index,pred_df['ll'],pred_df['ul'],alpha=0.2)
plt.legend(loc='upper left')
plt.ylabel('Number of Visitors (millons)')
plt.xlabel('Time (year)')
plt.show()
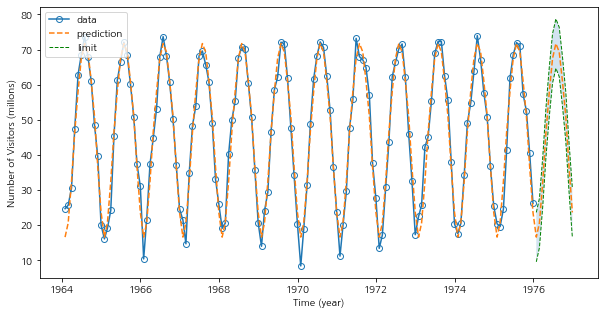
모형 적합이 꽤나 준수한 것 같다.
- 삼각함수를 사용한 모델링 -
이제 삼각함수를 이용하여 모델링해보자. 과정은 더미 변수를 사용한 모델링과 비슷하다. 먼저 time 열과 설명변수 행렬 $X$를 만들어준다. 이때 사인값과 코사인값이 정확히 0이 안되는 문제가 있어서 round 함수를 이용하여 소수 5째 자리만 구했다.
df['time'] = range(1,len(df)+1) ## time 변수 생성
f = 12
sin = []
cos = []
for time in df['time']:
angle = 2*np.pi*time/f
sin.append(round(np.sin(angle),5))
cos.append(round(np.cos(angle),5))
temp_data = {
'sin' : sin,
'cos' : cos
}
temp_df = pd.DataFrame(temp_data)
temp_df.index = pd.date_range(start_date,end_date,freq='m')
X = sm.add_constant(temp_df)
최소 제곱 추정량과 적합값을 구한다.
X_tX_inv = np.linalg.inv(X.T.dot(X))
bs = X_tX_inv.dot(X.T.dot(y.values)) ## estimated parameters
fitted_val = X.dot(bs) ## fitted values
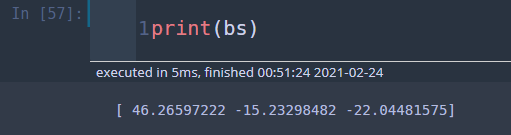
다음으로 1976년 1월부터 12월까지의 예측값과 예측구간을 구하고 시각화한다. 앞서 더미 변수를 이용한 모델링에서 했던 것과 거의 비슷하다.
future = list(range(1,13))
n = len(df)
alpha = 0.05
t_val = t.ppf(1-alpha/2,df=n-len(bs))
predict_vals = []
upper_limit = []
lower_limit = []
s2 = np.sum(np.square(y-fitted_val))/(n-len(bs))
for l in future:
sin_val = round(np.sin(2*np.pi*l/f),5)
cos_val = round(np.cos(2*np.pi*l/f),5)
x = np.array([1,sin_val,cos_val])
x = np.expand_dims(x,axis=1)
variance_factor = np.sqrt(1+x.T.dot(X_tX_inv.dot(x)))
limit = t_val*np.sqrt(s2)*variance_factor[0][0]
predict_val = x.T.dot(bs)[0]
predict_vals.append(predict_val)
upper_limit.append(predict_val+limit)
lower_limit.append(predict_val-limit)
strt_date = '1976-01-01'
pred_data = {
'pred':predict_vals,
'ul':upper_limit,
'll':lower_limit
}
pred_df = pd.DataFrame(pred_data)
pred_df.index = pd.date_range(strt_date,periods=future[-1],freq='m')
vals = pd.concat([fitted_val,pred_df['pred']])
fig = plt.figure(figsize=(10,5))
fig.set_facecolor('white')
marker_config = dict()
marker_config['marker'] = 'o'
marker_config['markerfacecolor'] = 'none'
plt.plot(df['tempdub'],label='data',**marker_config)
plt.plot(vals,label='prediction',linestyle='--')
lineconfig = dict()
lineconfig['linestyle'] = '--'
lineconfig['linewidth'] = 1
plt.plot(pred_df['ll'],color='green',**lineconfig,label='limit')
plt.plot(pred_df['ul'],color='green',**lineconfig)
plt.fill_between(pred_df.index,pred_df['ll'],pred_df['ul'],alpha=0.2)
plt.legend(loc='upper left')
plt.ylabel('Number of Visitors (millons)')
plt.xlabel('Time (year)')
plt.show()
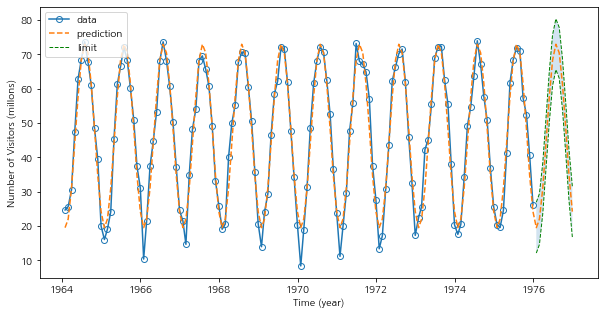
삼각함수를 이용한 모델링도 적합이 잘된 것 같다.
지금까지 최소 제곱법을 이용한 시계열 모델링 방법을 알아보았다. 시계열 데이터가 $Y_t = \mu_t + X_t$ 와 같은 구조를 따른다고 할 때 주의해야 할 점은 오차항에 해당하는 $X_t$가 반드시 독립이어야 한다는 것이다. 따라서 오차항이 독립성을 만족하지 않는다면 지금까지 살펴보았던 모델링 방법에 문제가 생길 소지가 있다. 따라서 모형을 적합한후 오차항이 독립인지 아닌지 확인해야한다. 특히 시계열 데이터에서는 오차항이 종속인 경우가 많은데 그러한 종속성 중에서 특히 자기 상관(Autocorrelation)성을 보이는 경우가 많이 있다. 다음 포스팅에서는 오차항이 자기 상관성을 보이는지 아닌지 검정하는 방법에 대해서 알아보고자 한다.
댓글