시계열 데이터가 무엇인지 정상 과정이 무엇인지 공부한 내용을 포스팅해보려고 한다. David Hitchcock 교수님 강의를 참고하였다. 이번 포스팅에서 다루는 내용은 다음과 같다.
1. 시계열 데이터란 무엇인가?
- 정의 -
시계열 데이터는 시간에 따라 같은 시간 간격(Equally Spaced)으로 또는 불규칙적(Unequally Spaced)으로 생산된 데이터를 말하며 데이터 속에 생성된 날짜, 시간 등이 포함된다.
- 특징 -
시계열 데이터는 그냥 데이터와 무엇이 다를까? 먼저 시계열 데이터는 일반적으로 이전 데이터와 종속 관계에 있다(Not independent). 또한 현시점에서 얻어진 데이터의 확률 분포는 다른 시점에서 얻어진 데이터의 확률 분포와 다를 수 있다(Not identitcal distributed). 또한 시계열 데이터에는 여러 패턴이 존재할 수 있는데 이를 실제 데이터를 통해서 알아보자. US Airline에서 1949년부터 1960년까지 비행기 이용 승객 수 데이터를 이용했다. 아래 그림은 데이터를 시각화해본 것이다.

1) 추세(Trend)
시계열 데이터에는 시간에 따라서 증가하거나 감소하는 패턴이 있을 수 있는데 이를 추세(Trend)라고 한다. 아래 그림은 US Airline 승객 수 데이터에서 일반적인 추세를 나타내는 직선을 추가하였다. 주황색 직선을 보면 승객 수는 시간이 지남에 따라 증가하는 추세가 있음을 알 수 있다.

2) 계절성(Seasonality)
계절성은 특정 주기를 기준으로 반복해서 나타나는 패턴이다. 아래의 데이터는 US Airline 승객 수에서 추세를 제외한 부분이다(추세를 제외하는 방법에 대해서는 추후 포스팅에서 다루겠다).

위 그림을 보면 대략 12개월 주기로 반복적인 패턴이 나타나는 것을 알 수 있다.
3) 순환성(Cyclicity)
순환성은 특정 데이터 값이 시간이 지나서 다시 나타나는 패턴을 말한다. 계절성 또한 특정 데이터 값이 시간이 지나서 다시 나타날 수 있으므로 다음과 같은 질문이 나올 수 있다.
그렇다면 계절성과 순환성의 차이가 무엇인가?
계절성은 데이터 값이 다시 나타나는 시기를 어느정도 특정할 수 있지만 순환성은 특정할 수 없다는 차이점이 있다. 예를 들어 특정 데이터 값이 4개월마다 다시 나타난다고 한다면 이는 계절성이지만 특정 데이터 값이 나타나는 시기가 3개월 후가 될 수도 있고 1년 이후가 될 수도 있다면 이는 순환성이다. 추가적으로 내 생각을 덧붙이면 순환성에서 다루는 패턴은 증가하다가 감소하는 패턴을 주로 다루는 데 반해 계절성은 좀 더 일반적인 패턴을 다루는 것 같다. 아래 데이터는 1821년부터 1934년까지 스라소니 트랩 수를 나타낸 것이며 순환성을 나타내는 데이터라 할 수 있다.

이때 trapping 개수가 1000인 경우를 살펴보자.

위 그림에서 알 수 있듯이 특정 지점에서 1000이 나타난 경우 다음 1000이 나타나기까지 걸리는 시간의 간격이 일정하지 않다(따라서 이 데이터는 순환성을 갖는다).
2. Stationary Process 란?
Stationary Process를 이야기 하기 위해 사전에 알아야 할 개념에 대해서 알아보자. 시계열 데이터 {Yt:t=…,−2,−1,0,1,2,…}가 있다고 하자. 그리고 다음과 같이 t에서의 평균을 μt=E(Yt), 자기 공분산 함수(Auto-covariance function)를 γt,s=cov(Yt,Ys) 그리고 자기 상관 함수(Auto-correlation function)를 ρt,s=corr(Yt,Ys)라 하자.
여기서
corr(Yt,Ys)=cov(Yt,Ys)[var(Yt)var(Ys)]1/2
이다.
Stationary Process에 대해서 알아보자. 먼저 Strict Stationary Process에 대해서 알아보자.
1) Strict Stationary Process(SSP)
Random Process {Yt:…,−2,−1,0,1,2,…}가 있다고 하자. 모든 양의 정수 k와 모든 정수 h에 대하여 (Yt1,…,Ytk)의 결합 확률 분포와 (Yt1+h,…,Ytk+h)의 결합 확률 분포가 같을 때 {Yt:…,−2,−1,0,1,2,…}을 Strict Stationary Process라 한다.
2) Weak Stationary Process(WSP)
Random Process {Yt:…,−2,−1,0,1,2,…}가 다음을 만족한다고 할 때 Xt는 Weak Stationary Process라고 한다.
(i) 모든 정수 t에 대하여 E|Yt|2<∞
(ii) 모든 정수 t에 대하여 E(Yt)=μ
(III) 모든 정수 t, r, s에 대하여 γr,s=γr+t,s+t
WSP의 조건 (ii)는 Yt의 기대값이 시간에 따라 변하지 않는다는 뜻이며 조건 (iii)에서 t=−s라 한다면 γr,s=γr−s,0이 되고 이는 WSP의 공분산 함수는 시간의 차이에만 의존한다는 것이다. Weak Stationary Process는 Covariance Stationary, Wide Sense Stationary, Second Order Stationary Process라고도 한다.
이름에서 알 수 있듯이 Yt가 SSP라면 E|Yt|2<∞인 경우 WSP가 된다. 그 이유를 살펴보자. Yt를 SSP라 하자. SSP의 정의에서 k=1,t1=t라 하자. 그렇다면 Yt는 모든 t에 대해서 같은 확률분포를 가지므로 E(Yt)는 시간에 따라서 변하지 않는다. 또한 k=2라 하고 t1=r,t2=s라 하면 (Yr,Ys)의 결합 분포는 (Yr+t,Ys+t)의 분포가 같다. 따라서 공분산 함수 또한 서로 같다.
하지만 역은 성립하지 않는다. 즉, WSP라고 해서 SSP인 것은 아니다. Yt를 독립인 Random Process라고 하고 t가 홀수인 경우 평균이 1인 지수 분포를 따르는 확률 변수, 짝수인 경우 평균이 1, 분산이 1인 정규분포를 따르는 확률 변수라 한다면 이는 WSP이지만 SSP는 아니다.
- 왜 Stationary Process가 필요한가?
시계열 데이터에서는 아래 그림과 같이 데이터를 생성하는 확률 분포가 매시점마다 다를 수 있다.
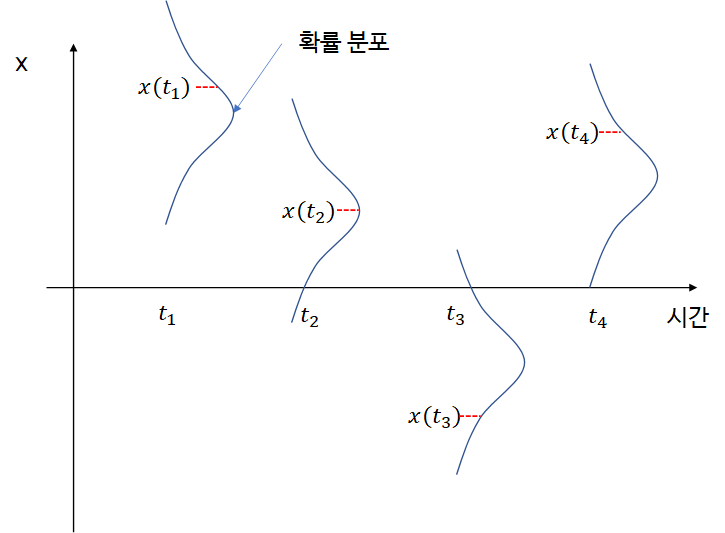
특히 데이터 분석에서는 평균을 구하는 것이 주된 관심사인데 이러한 경우 평균을 어떻게 구할 것인지에 대한 어려움이 생기게 된다. 매시점마다 확률 분포가 다른 상황에서 해당 확률 분포의 평균을 구한다고 한다면 매시점 하나의 데이터를 이용하여 평균을 추정해야 되니 추정의 정확성이 떨어진다. 그렇기 때문에 우리는 위 그림에서 4개의 데이터를 모두 이용하고 싶을 것이다. 이 경우 다음과 같은 값을 생각해볼 수 있다.
144∑i=1x(ti)
그렇다면 이 값은 의미가 있는 것일까? 그것도 아닐 것이다. 왜냐하면 각각의 데이터가 다른 확률 분포로부터 나온 샘플이기 때문에 이 값이 타게팅하는 모수가 무엇인지 명확하지 않기 때문이다.
이때 x(t)가 SSP라면 모든 문제는 해결된다. 즉, 시계열 데이터로부터 우리가 알고 있는 단순 표본 샘플을 구하면 이는 하나의 분포로부터 나온 샘플을 계산한 것이며 해당 확률 분포의 평균을 추정하게 된다. 즉, 우리가 기존 데이터 분석에서 사용하는 통계량을 시계열 데이터에서도 기본적으로 사용할 수 있게 하는 최소한의 조건이 Strict Stationarity인 것이다(실제 시계열 데이터에서 계산한 표본 평균이 모 평균으로 수렴하기 위한 조건은 Erogodicity인데 이는 Strict Stationarity보다 더 강한 조건이다). Weak Stationarity는 Strict Stationarity를 약화시킨 것이며 시계열 관련 수학적인 이론 전개에서 필요한 조건으로 활용된다.
참고자료
Brockwell, Davis - Time Series: Theory and Methods

'통계 > 시계열 모형' 카테고리의 다른 글
| [시계열 분석] 6. 이동 평균 모형(Moving Average Model) 적합하기 with Python (809) | 2021.08.20 |
|---|---|
| [시계열 분석] 5. 자기 상관 함수(Autocorrelation Function : ACF)과 부분 자기 상관 함수(Partial Autocorrelation : PACF) with Python (1038) | 2021.07.31 |
| [시계열 분석] 4. 자기 회귀 모형(Autoregressive Model) 적합하기 with Python (1434) | 2021.04.09 |
| [시계열 분석] 3. (General) Durbin-Watson 검정 with Python (1118) | 2021.03.21 |
| [시계열 분석] 2. 최소 제곱법을 이용한 시계열 분석 with Python (1) | 2021.02.24 |





댓글