이번 포스팅에서는 시계열 모형 중 하나인 자기 회귀 모형(Autoregressive Model : AR)에 대해서 알아보고 파이썬으로 구현해보고자 한다. 또한 statsmodels을 사용하여 자기 회귀 모형을 추정하거나 예측하는 방법에 대해서도 소개한다.
1. 자기 회귀 모형이란 무엇인가?
자기 회귀 모형을 정의하기 이전에 백색 잡음의 정의를 알아보자.
- 백색 잡음 -
정상성을 가지는 시계열 $Z_t , t=1, \ldots, n$ 에 대하여 $E(Z_t) = 0$, $\gamma_Z(h) = E(Z_tZ_{t-h})$라 하자. 이때 $\gamma_Z(h) = \sigma^2I(h=0)$을 만족하는 경우 $Z_t$를 백색 잡음(White Noise)이라 한다. 여기서 $I(h=0)$은 $h=0$ 인 경우 1, 그 외의 경우에는 0을 갖는 함수이다. 즉, 백색 잡음은 정상성을 만족하는 시계열 중에서 평균이 0이고 분산이 $\sigma^2$이며 자기 상관이 존재하지 않는 시계열을 말한다.
- 자기 회귀 모형 -
이제 정상성을 갖는 시계열 $X_t, t=1, \ldots, n$이 다음과 같은 관계가 있다고 하자.
$$X_t = c+\phi_1X_{t-1}+\phi_2X_{t-2}+\cdots+\phi_pX_{t-p}+Z_t\tag{1-1}$$
이때 $Z_t$는 평균이 0이고 분산이 $\sigma^2$인 백색 잡음이며 $X_{t-j} \;(j=1, 2, \ldots, p)$ 와 독립이다.
이러한 관계를 $p$차 자기 회귀 모형(Autoregressive Model : AR($p$))이라 하며 $X_t$는 $p$차 자기 회귀 과정을 따른다고 한다($X_t, Z_t$는 확률 변수이다). 즉, AR($p$)는 현재 시계열 값이 이전 시점 시계열 값들의 선형 결합과 백색 잡음의 합으로 이루어진 모형이다. 이는 현재 또는 이전 데이터로부터 미래 데이터를 예측하기 위한 모형이다.
식 (1-1)을 바꿔보자. $X_t$가 정상성을 가지므로 $\mu=E(X_t)=E(X_{t-1})=\cdots=E(X_{t-p})$이다. 식 (1-1) 양변에 기대값을 취하면 다음과 같음을 알 수 있다.
$$\mu = c+(\phi_1+\cdots+\phi_p)\mu$$
따라서 $c = (1-\phi_1-\cdots-\phi_p)\mu$이고 이를 식 (1-1)에 대입하면 아래의 식을 얻을 수 있다.
$$X_t-\mu = \phi_1(X_{t-1}-\mu)+\phi_2(X_{t-2}-\mu)+\cdots+\phi_p(X_{t-p}-\mu)+Z_t\tag{1-2}$$
2. 언제 사용하는가?
자기 회귀 모형은 다음과 같이 2가지 상황을 만족한다면 사용해볼 수 있다.
1. 시계열 데이터가 정상성을 가지는 경우
-> ADF Test, KPSS Test를 이용하여 해당 시계열 데이터가 정상 과정인지 검정할 수 있다.
2. 현재 데이터가 과거 데이터와 독립이 아닌 경우, 다시 말해서 과거 데이터가 현재 데이터에 영향을 미친다는 합리적인 판단이 드는 경우
-> ACF, PACF를 그려서 확인할 수 있다.
3. 모형 추정 방법
모형 추정이라는 말은 $\mu, \phi_1, \ldots, \phi_p$ 그리고 $\sigma^2$를 추정한다는 것이다. 모형을 추정하기 위해서는 차수$p$를 설정해야하는데 이는 부분 자기 상관 함수(Partial Autocorrelation Function : PACF)를 여러 차수(예 1~20)에 대해서 그려본 다음 특정 차수에서 그 값이 확 떨어진다면 바로 전 시점을 $p$로 설정한다. 예를 들어 3차 PACF 값이 확 떨어졌다면 차수를 2로 정한다.
자기 상관 함수와 부분 자기 상관 함수에 대한 설명은 아래에 포스팅 해놓았으니 참고하기 바란다.
[시계열 분석] 5. 자기 상관 함수(Autocorrelation Function : ACF)과 부분 자기 상관 함수(Partial Autocorrelatio
본 포스팅에서는 수식을 포함하고 있습니다. 티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니 PC 웹 브라우저 또는 모바일 웹 브라우저에서 보시기 바랍니다. 이번 포스팅에서는 자
zephyrus1111.tistory.com
AR($p$) 모형에서 $\mu, \phi_1, \ldots, \phi_p, \sigma^2$은 여러 가지 방법으로 추정할 수 있다. 여기서는 다루는 추정방법은 다음과 같다.
1) 최소 제곱 추정법
$X_t, \;t=1, \ldots, n$의 관측치를 $x_t$라 하자. 최소 제곱 추정법은 다음의 $S$를 최소화하는 $\mu, \phi_i, \;i=1, \ldots, p$를 찾는 방법이다.
$$S = \sum_{t=p+1}^n[x_t-\mu-\phi_1(x_{t-1}-\mu)-\cdots-\phi_p(x_{t-p}-\mu)]^2\tag{3-1}$$
최소 제곱 추정법에는 근사적인 방법을 이용하는 방법과 비선형 최소 제곱법을 이용하여 정확하게 추정하는 방법이 있다. 이에 대해서 알아보자.
(1) 근사적인 방법을 이용하는 방법
먼저 $n$이 $p$보다 충분히 크다고 하자.
$S$를 최소화하는 $\mu$는 다음의 식을 만족해야 한다.
$$\frac{\partial S}{\partial \mu} = -2\sum_{t=p+1}^n[x_t-\mu-\phi_1(x_{t-1}-\mu)-\cdots-\phi_p(x_{t-p}-\mu)] = 0\tag{3-2}$$
식 (3-2)을 만족하는 $\mu$를 $\hat{\mu}$라 하면 아래와 같이 구할 수 있다.
$$\hat{\mu} = \frac{1}{(n-p)(1-\phi_1-\cdots-\phi_p)}\sum_{t=p+1}^n(x_t-\phi_1x_{t-1}-\cdots-\phi_px_{t-p})\tag{3-3}$$
$n$이 $p$보다 충분히 큰 경우,
$$\bar{x}=\frac{1}{n}\sum_{t=1}^nx_t\approx \frac{1}{n-p}\sum_{t=p+1}^nx_{t-1}\approx \cdots \approx \frac{1}{n-p}\sum_{t=p+1}^nx_{t-p}$$
라고 할 수 있다. 이를 식 (3-3)에 적용하면 $\hat{\mu}\approx \bar{x}$이다. 즉, $\mu$는 일반적인 표본 평균으로 추정한다.
이제 나머지 파라미터를 추정하기 위하여 $\hat{\mu}$를 식 (3-1)의 $\mu$에 집어넣는다.
$$S = \sum_{t=p+1}^n[x_t-\bar{x}-\phi_1(x_{t-1}-\bar{x})-\cdots-\phi_p(x_{t-p}-\bar{x})]^2$$
이는 종속변수가 $x_t-\bar{x}$이고 설명변수가 $x_{t-1}-\bar{x}, \ldots, x_{t-p}-\bar{x}$인 선형 회귀 모형을 적합하는 것으로 볼 수 있다. 따라서 일반적인 최소 제곱법을 이용하여 $\phi_1, \ldots \phi_p$를 추정하면 된다.
(2) 비선형 최소 제곱법
비선형 최소 제곱법은 근사적인 방법을 이용했던 것과 달리 $S$를 최소화하는 파라미터를 직접 구하는 방법이다.
$y_i=x_i, \tilde{z}_i=(x_{i-1},\ldots,x_{i-p})^t, \tilde{\beta}=(\mu, \phi_1, \ldots, \phi_p)^t$라 하고 $$f(\tilde{z}_i, \tilde{\beta}) = \mu+\phi_1(x_{i-1}-\mu)+\cdots+\phi_p(x_{i-p}-\mu)$$
라 하자. 이 경우 식 (3-1)은 다음과 같이 쓸 수 있다($t$를 $i$로 바꿨다).
$$S = \sum_{i=p+1}^n[y_i-f(\tilde{z}_i, \tilde{\beta})]^2\tag{3-4}$$
식 (3-4)를 보면 최소 제곱법과 비슷해 보이지만 $f$가 $\mu, \phi_1, \ldots, \phi_p$에 대하여 비선형이므로 비선형 최소 제곱법이라 한다. 일반적인 최소 제곱 법과는 달리 비선형 최소 제곱법은 파라미터를 직접적으로 구할 수 없다. 따라서 수치적인 방법으로 구해야 한다.
비선형 최소 제곱법에 대한 구체적인 설명은 위키를 참고하자. 여기서는 비선형 최소 제곱법을 이용하여 AR($p$) 모형을 추정하는 알고리즘에 대해서 알아본다.
$k$ 번째 스텝에서 얻은 파라미터 값을 $\tilde{\beta}^k = (\beta_1^k, \beta_2^k, \ldots, \beta_{p+1}^k) = (\mu^k, \phi_1^k, \ldots, \phi_p^k)$라 하자. 이제 $k+1$ 번째 파라미터 값을 구하기 위하여 $\Delta\tilde{\beta}$를 구할 것이다. $\Delta\tilde{\beta}$를 구하기 위해선 자코비안 행렬 $J$을 구해야 한다. 여기서 $(n-p)\times (p+1)$ 행렬 $J$는 다음과 같다.
$$J_{ij} = \frac{\partial f(\tilde{z}_i, \tilde{\beta}^k)}{\partial \beta_j}, \; i=1, 2, \ldots, n-p, j=1, 2, \ldots, p+1$$
($\beta_1 = \mu, \beta_{j} = \phi_{j-1}, \;\;j=2, \ldots, p+1$ 이다.)
주어진 $i$에 대하여 $J_{ij}$를 계산하면 다음과 같다.
$$J_{i1} = \frac{\partial f(\tilde{z}_i, \tilde{\beta}^k)}{\partial \beta_1} = \frac{\partial f(\tilde{z}_i, \tilde{\beta}^k)}{\partial \mu} = 1-\phi_1^k-\cdots-\phi_p^k$$
$$J_{ij} = \frac{\partial f(\tilde{z}_i, \tilde{\beta}^k)}{\partial \beta_j} = \frac{\partial f(\tilde{z}_i, \tilde{\beta}^k)}{\partial \phi_{j-1}} = x_{i-j}-\mu^k, \;\;j = 2, \ldots, p+1$$
$\Delta \tilde{y}=(\Delta_{p+1}, \ldots, \Delta_{n})^t$, $\Delta_i = y_i-f(\tilde{z}_i, \tilde{\beta}^k)$라 할때 $\Delta\tilde{\beta}$는 다음을 만족하는 벡터이다.
$$J^tJ\Delta\tilde{\beta} = J^t\Delta\tilde{y}\tag{3-5}$$
AR($p$) 모형을 추정하는 알고리즘은 다음과 같다.
알고리즘
1 단계) 초기값 $\tilde{\beta}^0$과 오차범위 $\epsilon$ 설정한다. 초기값의 경우 앞서 살펴보았던 근사적인 방법을 이용한 추정값을 초기값으로 한다.
2 단계) $k$ 번째 스텝에서 얻은 파라미터 값을 $\tilde{\beta}^k$라 하면 식 (3-5)에서 구한 $\Delta\tilde{\beta}$을 이용하여 다음과 같이 업데이트한다.
$$\tilde{\beta}^{k+1} \leftarrow \tilde{\beta}^k + \Delta\tilde{\beta}$$
3 단계) 모든 $j$에 대하여 $\left |\frac{\beta_j^{k+1}-\beta_j^k}{\beta_j^k} \right |<\epsilon$ 이면 알고리즘을 종료하고 아니면 2 단계)로 돌아간다.
(3) 백색 잡음의 분산 추정
(1), (2)에서 추정한 모수를 식 (3-1) 또는 (3-4)에 집어넣어서 계산된 $S$를 $S^*$라 하자. 백색 잡음의 분산 $\sigma^2$은 다음과 같이 추정할 수 있다.
$$\hat{\sigma}^2 = \frac{1}{n-p}S^*$$
이 추정량은 사실 아래에서 다룰 Conditional MLE 방법으로 구한 분산 추정량과 같다.
2) 최대 우도 추정법
AR($p$) 모형의 파라미터 $\mu, \phi_1, \ldots, \phi_p$는 최대 우도 추정법(Maximum Likelihood Estimation : MLE)을 이용하여 추정할 수 있다. MLE를 이용한 추정방법에는 Unconditional MLE와 Conditional MLE가 있다. 여기서는 식 (1-2) 대신 식 (1-1)을 사용하며 백색 잡음 $Z_t$이 독립이고 동일한 정규분포 $N(0, \sigma^2)$를 따른다고 가정한다. 이제 각각의 방법을 알아보자.
(1) Unconditional MLE
Unconditional MLE은 $X_1, X_2, \ldots, X_n$의 결합 확률 분포를 우도 함수로 놓고 이를 최대화하는 파라미터이다. $X_1, X_2, \ldots, X_n$의 결합 확률 분포를 구해보자.
$X_1, \ldots, X_p$가 평균 벡터가 $\mu_p=(\mu_1, \mu_2, \ldots, \mu_p)$, 공분산 행렬이 $\sigma^2V_p$인 $p$ 차원 정규분포를 따른다고 하자. $X_t, \;(t=1, \ldots, n)$이 정상성을 갖기 때문에 $\mu_p$의 원소는 모두
$$\mu = \mu_1 = \cdots = \mu_p = c/(1-\phi_1 - \cdots - \phi_p)$$
이며 $\sigma^2V_p$는 다음과 같다.
$$\sigma^2V_p=
\begin{pmatrix}
\gamma_0 & \gamma_1 & \cdots & \gamma_{p-1} \\
\gamma_1 & \gamma_0 & \cdots & \gamma_{p-2} \\
\vdots & \vdots & \ddots & \vdots \\
\gamma_{p-1} & \gamma_{p-2} & \cdots & \gamma_0
\end{pmatrix}$$
이 경우 추정해야 할 파라미터는 $\theta = (c, \phi_1, \ldots, \phi_p, \gamma_0, \ldots, \gamma_{p-1},\sigma^2)^t$이며 $X_1, \ldots, X_p$의 결합 확률 밀도 함수는 다음과 같다.
$$f_{X_p, X_{p-1}, \ldots, X_1}(x_p, x_{p-1}, \ldots, x_1; \theta) \\ = (2\pi\sigma^2)^{-p/2}|V_p^{-1}|^{1/2} \exp\left[ \frac{1}{2\sigma^2}(\tilde{x}_p-\mu_p)^tV_p^{-1}(\tilde{x}_p-\mu_p)\right]\tag{3-6}$$
여기서 $\tilde{x}_p = (x_1, \ldots, x_p)^t$ 이다.
그리고
$$f_{X_n, \ldots, X_{p+1}|X_p, \ldots, X_1}(x_n, \ldots, x_{p+1} ; \theta) = \prod_{j=p+1}^nf_{X_j|X_{j-1},\ldots,X_{j-p}}(x_j;\theta) \\ = \prod_{j=p+1}^n\frac{1}{\sqrt{2\pi}\sigma}\exp \left\{-\frac{1}{2\sigma^2}(x_j-c-\phi_1x_{j-1}-\cdots-\phi_px_{j-p})^2 \right\}\tag{3-7}$$
이다. 첫 번째 등식은 $X_j(j>p)$는 $X_{j-1}, \ldots, X_{j-p}$에 의존하기 때문이며, 두 번째 등식은 $Z_t$가 평균이 0, 분산이 $\sigma^2$인 정규분포를 따르는 독립변수이기 때문에 성립한다.
식 (3-6), (3-7)을 이용하면 $X_1, X_2, \ldots, X_n$의 결합 확률 분포를 구할 수 있다.
$$f_{X_n, X_{n-1}, \ldots, X_1}(x_n, x_{n-1}, \ldots, x_1; \theta) \\ = f_{X_p, X_{p-1}, \ldots, X_1}(x_p, x_{p-1}, \ldots, x_1; \theta) f_{X_n, \ldots, X_{p+1}|X_p, \ldots, X_1}(x_n, \ldots, x_{p+1} ; \theta)$$
위 식에서 양변에 로그를 취하고 계산하면 로그 우도 함수는 다음과 같다.
$$L(\theta) = \log f_{X_n, X_{n-1}, \ldots, X_1}(x_n, x_{n-1}, \ldots, x_1; \theta)$$
$$\begin{align} = &-\frac{n}{2}\log (2\pi\sigma^2)+\frac{1}{2}\log |V_p^{-1}| \\ &-\frac{1}{2\sigma^2}(\tilde{x}_p-\mu_p)^tV_p^{-1}(\tilde{x}_p-\mu_p) \\ &- \sum_{j=p+1}^n\frac{(x_j-c-\phi_1x_{j-1}-\cdots-\phi_px_{j-p})^2}{2\sigma^2}\end{align}\tag{3-8}$$
식 (3-8)을 계산하려면 $V_p^{-1}$을 계산해야 한다. $V_p^{-1}$의 $i$ 번째 행, $j$ 번째 열 원소 $v_{ij}$는 다음과 같다.
$$v_{ij} = \sum_{k=0}^{i-1}\phi_k\phi_{k+j-i} - \sum_{k=p+1-j}^{p+i-j}\phi_k\phi_{k+j-i}$$
이때 $\phi_0 = -1$이다.
Unconditional MLE는 미분식이 복잡하여 일반적으로 Newton-Rhapson 방법과 같은 수치적인 방법을 이용하여 계산한다. 나는 Davidavidon-Fletcher-Powell 방법으로 Unconditional MLE를 구하려고 한다.
먼저 주어진 $\sigma^2$에 대하여 $g(\theta) = \frac{\partial L(\theta)}{\partial \theta}$를 구해야 한다. 여기서는 $\sigma^2$과 나머지 파라미터를 따로 구하기 위하여 $\theta = (c, \phi_1, \ldots, \phi_p)$라 하겠다.
$$\frac{\partial L(\theta)}{\partial c} = -\frac{1}{2\sigma^2}\left[2\mu\frac{\partial \mu}{\partial c}\sum_{1\leq i,j \leq p}v_{ij}-2\frac{\partial \mu}{\partial c}\sum_{1\leq i,j \leq p}x_iv_{ij}\right] \\ + \frac{1}{\sigma^2}\sum_{t=1}^p(x_t-c-\phi_1x_{t-1}-\ldots-\phi_px_{t-p})$$
여기서 $\partial \mu/\partial c = (1-\phi_1-\ldots-\phi_p)^{-1}$이다.
그리고 $m = 1, \ldots, p$에 대하여
$$\frac{\partial L(\theta)}{\partial \phi_m} = \frac{1}{2} \text{tr}\left(V_p\frac{d V_p^{-1}}{d \phi_m}\right) \\ - \frac{1}{\sigma^2}\sum_{1\leq i,j \leq p} \left(\mu\frac{\partial \mu}{\partial \phi_m}v_{ij} + \mu^2\frac{\partial v_{ij}}{\partial \phi_m} -\frac{\partial \mu}{\partial \phi_m}x_iv_{ij}-\mu x_i\frac{\partial v_{ij}}{\partial \phi_m}\right) \\ +\frac{1}{\sigma^2}\sum_{t=p+1}^n\{(x_t-c-\phi_1x_{t-1}-\cdot-\phi_px_{t-p})x_{t-m}\}$$
여기서 $\partial \mu/\partial \phi_m = c/(1-\phi_1-\cdots-\phi_p)^2$이고
$$\frac{\partial V_p^{-1}}{\partial \phi_m} = \frac{\partial v_{ij}}{\partial \phi_m}_{1\leq i,j \leq p}$$
$$\small{\frac{\partial v_{ij}}{\partial \phi_m} = \begin{cases}
2\phi_m I(1\leq m \leq i-1)-2\phi_m I(p+1-j\leq m \leq p), & \text{if}\ i=j \\
\phi_{m+j-i}I(1\leq m\leq i-1)+\phi_{m-j+i}I(j-i\leq m \leq j-1) \\ - \phi_{m+j-i}I(p+1-j\leq m \leq p+i-j)-\phi_{m-j+i}I(p+1-i\leq m \leq p), & \text{if}\ j>i
\end{cases}} $$
따라서
$$g(\theta) = \left(\frac{\partial L(\theta)}{\partial c}, \frac{\partial L(\theta)}{\partial \phi_1}, \ldots \frac{\partial L(\theta)}{\partial \phi_p}\right )^t$$
이다. $g(\theta)$ 계산이 힘들다면 Finite Difference 방법을 이용해도 좋다.
Davidavidon-Fletcher-Powell 방법으로 Unconditional MLE를 구하는 알고리즘은 다음과 같다.
알고리즘
1 단계) 초기값 $\sigma^{2(0)}, \theta^{(0)}, A^{(0)}$과 오차범위 $\epsilon$을 설정한다. 최소 제곱법을 이용하여 추정한 파라미터와 이에 대응하는 백색 잡음 분산 추정치를 초기값으로 이용한다. 그리고 $A^{(0)}$는 Hessian 행렬의 역행렬로 설정하며 Hessian 행렬은 $\theta^{(0)}$에서 Finite Difference를 이용하여 근사 시킨다.
2 단계) $m$번째 스텝에서 다음을 최대화하는 실수 $s$를 찾는다.
$$L(\theta^{(m)}+sA^{(m)}g(\theta^{(m)}))$$
이때 최대값을 $L^{(m)}$로 저장하고 이에 해당하는 $s$를 $s^*$라 하자. 만약 $L^{(m)} \leq L^{(m-1)}$이면 알고리즘을 종료한다.
3 단계) 파라미터들을 다음과 같이 업데이트한다.
$$\theta^{(m+1)} = \theta^{(m)}+s^*A^{(m)}g(\theta^{(m)})$$
그리고 백색 잡음의 분산은 다음과 같이 업데이트한다.
$$\small{\sigma^{(m+1)} = \frac{1}{n}\left[ (\tilde{x}_p-\mu_p^{(m)})^tV_p^{-1(m)}(\tilde{x}_p-\mu_p^{(m)}) + \sum_{t=p+1}^n(x_t-c-\phi_1^{(m)}x_{t-1}-\cdots-\phi_p^{(m)}x_{t-p})^2\right ]}$$
그리고 $A$는 다음과 같이 업데이트한다.
$$A^{(m+1)} = A^{(m)}-\frac{A^{(m)}(\Delta g^{(m+1)}) (\Delta g^{(m+1)})^tA^{(m)} }{(\Delta g^{(m+1)})^t A^{(m)}(\Delta g^{(m+1)})} \\ - \frac{(\Delta \theta^{(m+1)})(\Delta \theta^{(m+1)})^t}{(\Delta g^{(m+1)})^t(\Delta \theta^{(m+1)})}$$
여기서
$$\Delta \theta^{(m+1)}) = \theta^{(m+1)})-\theta^{(m)}) \\ \Delta g^{(m+1)} = g(\theta^{(m+1)})-g(\theta^{(m)})$$
이다.
4 단계) $A^{(m+1)}$이 양정치 행렬이 아닌 경우 또는 파라미터 값들의 차이 $\|\Delta \theta^{(m+1)})\|$가 $\epsilon$보다 작다면 알고리즘을 종료한다.
(2) Conditional MLE
$x_1, \ldots, x_p$가 주어졌다고 하자. Conditional MLE는 다음과 같이 조건부 우도 함수를 최대화하는 파라미터 $\theta = (c, \phi_1, \ldots, \phi_p, \sigma^2)^t$가 된다.
$$f_{X_n, \ldots, X_{p+1}|X_p, \ldots, X_1}(x_n, \ldots, x_{p+1} ; \theta) = \prod_{j=p+1}^nf_{X_j|X_{j-1},\ldots,X_{j-p}}(x_j;\theta)$$
$$\begin{align} = \prod_{j=p+1}^n\frac{1}{\sqrt{2\pi}\sigma}\exp \left\{-\frac{1}{2\sigma^2}(x_j-c-\phi_1x_{j-1}-\cdots-\phi_px_{j-p})^2 \right\}\end{align}$$
위 식에서 양변에 로그를 취해준다.
$$ \log f_{X_n, \ldots, X_{p+1}|X_p, \ldots, X_1}(x_n, \ldots, x_{p+1} ; \theta) \\ = (n-p)\log\frac{1}{\sqrt{2\pi}\sigma} + \sum_{j=p+1}^n\left\{-\frac{1}{2\sigma^2}(x_j-c-\phi_1x_{j-1}-\cdots-\phi_px_{j-p})^2 \right\}$$
이제 위 식을 최대화하는 파라미터 $c, \phi_1, \ldots, \phi_p$을 찾아야 한다. 이는 아래의 식을 최소화하는 파라미터를 찾는 것과 동일하다.
$$\sum_{j=p+1}^n(x_j-c-\phi_1x_{j-1}-\cdots-\phi_px_{j-p})^2$$
앞서 살펴보았던 최소 제곱법을 통하여 위 식을 최소화하는 $c, \phi_1, \ldots, \phi_p$을 찾을 수 있다. 이를 $\hat{c}, \hat{\phi_1}, \ldots, \hat{\phi_p}$라 하자. $\sigma^2$은 다음과 같이 추정한다.
$$\hat{\sigma}^2 = \frac{1}{n-p}\sum_{j=p+1}^n(x_j-\hat{c}-\hat{\phi_1}x_{j-1}-\cdots-\hat{\phi_p}x_{j-p})^2$$
Conditional MLE는 Unconditional MLE보다 계산 과정이 훨씬 쉽다.
3) Yule-Walker 방정식을 이용한 추정법
Yule-Walker 방정식을 이용한 추정법은 적률을 이용하여 파라미터 $\mu, \phi_1, \ldots, \phi_p, \sigma^2$를 추정하는 방법이다.
식 (1-2) 양변에 $X_{t-k} - \mu, k=0, 1, \ldots, p$ 를 곱하고 기대값을 취하면 다음과 같음을 알 수 있다.
$$\gamma_k = \sum_{j=1}^p\phi_j\gamma_{j-k} + \sigma^2 I(k=0)\tag{3-6}$$
여기서 $\gamma_k = \text{cov} (X_t,X_{t-k})$이다.
$k=0$인 경우를 제외하면 식 (3-6)은 다음과 같이 표현할 수 있다.
$$
\begin{pmatrix}
\gamma_1 \\
\gamma_2 \\
\vdots \\
\gamma_p
\end{pmatrix} =
\begin{pmatrix}
\gamma_0 & \gamma_1 & \cdots & \gamma_{p-1} \\
\gamma_1 & \gamma_0 & \cdots & \gamma_{p-2} \\
\vdots & \vdots & \ddots & \vdots \\
\gamma_{p-1} & \gamma_{p-2} & \cdots & \gamma_0
\end{pmatrix} \begin{pmatrix}
\phi_1\\
\phi_2\\
\vdots \\
\phi_p
\end{pmatrix} \tag{3-7}$$
$k = 0$인 경우
$$\gamma_0 = \sum_{j=1}^p\phi_j\gamma_j+\sigma^2 \tag{3-8}$$
이다.
Yule-Walk 방법의 핵심은 바로 $\gamma_k$를 적률 추정량을 이용한다는 것이다. 즉,
$$\hat{\gamma}_k = \frac{1}{n}\sum_{t=k+1}^n(x_t-\bar{x})(x_{t-k}-\bar{x})$$
Yule-Walk 방정식을 이용한 파라미터 추정법은 다음과 같다.
Yule-Walk 방정식을 이용한 파라미터 추정법
1 단계) $\mu$는 $\sum_{t=1}^nx_t/n$으로 추정한다.
2 단계) $\phi_1, \ldots, \phi_p$는 식 (3-7)에서 $\gamma_k$를 $\hat{\gamma}_k$로 대입하고 역행렬을 이용하여 추정한다.
3 단계) $\phi_1, \ldots, \phi_p$의 추정값과 $\hat{\gamma}_k$를 식 (3-8)에 대입하여 $\sigma^2$의 추정치를 계산한다.
이제 백색 잡음의 분산을 추정해보자. 식 (3-8)을 정리하면 다음과 같다.
$$\sigma^2 = (1-\phi_1\rho_1 - \cdots - \phi_p\rho_p)\gamma_0\tag{3-9}$$
여기서 $\rho_k = \gamma_k/\gamma_0$ 이다. 이제 표본 분산 $s^2=\sum_{t=1}^n(x_t-\bar{x})^2/n$ ($\gamma_0$ 는 $X_t$의 분산임을 기억하자)과 표본 자기 상관계수 $r_k=\sum_{t=k+1}^n(x_t-\bar{x})(x_{t-k}-\bar{x})/s^2$ 그리고 Yule-Walk 방정식을 이용하여 계산한 $\hat{\phi}_k$을 식 (3-9)에 집어넣자. 그러면 다음과 같이 백색 잡음의 분산을 추정할 수 있다.
$$\hat{\sigma}^2 = (1-\hat{\phi}_1r_1 - \cdots - \hat{\phi}_pr_p)s^2$$
4) Large Sample Property
앞서 세 가지 방법으로 구한 파라미터 $\hat{\phi} = (\hat{\phi}_1,\ldots,\hat{\phi}_p)^t$에 대하여 적절한 조건하에서 다음과 같은 사실이 알려져 있다.
$$\sqrt(n)(\hat{\phi} - \phi) \rightarrow N(0, \hat{\sigma}^2\Gamma_p^{-1})$$
여기서 $\Gamma_p^{-1}$은 식 (3-7)에서 나타난 $p\times p$ 행렬이다. 이러한 성질을 이용하면 $\phi$의 신뢰구간과 추정량의 분산을 추정할 수 있다.
5) 파이썬 코드
필요한 모듈을 임포트해주자.
import pandas as pd
import numpy as np
np.seterr(divide='ignore', invalid='ignore')
import matplotlib.pyplot as plt
from scipy.stats import norm
먼저 클래스를 하나 정의하고 적절한 값을 초기화해준다.
class autoRegressiveModel():
def __init__(self,data,p):
self.p = p ## 차수
self.data = data ## 데이터
self.mu = None ## 기대값의 추정량
self.phi = None ## 모수의 추정량
self.fitted_values = None ## 적합값
self.method = None ## 추정 방법
self.mle_method = None ## 최대 우도 추정방법
self.intercept = None ## 절편 추정량
self.error_variance = None ## 백색잡음 분산
self.log_likelihood = None ## 최대 우도 추정값
self.std_error = None ## 모수 추정량의 표준오차
다음으로 모형 적합 과정을 구현한다. 모형 적합 과정은 1) 모수 추정, 2) 모형 적합값 계산, 3) 백색 잡음 계산, 4) 표준 오차 계산 순으로 이루어진다.
class autoRegressiveModel():
''' 생략 '''
def fit(self,method='Approx LS',tolerance=0.0001,grad_method='approx'):
self.method = method
valid_methods = ['Approx LS','Non-linear LS','YW','CMLE','EMLE']
assert method in valid_methods, \
f'method argument must be the one of {valid_methods}'
## 1) 모수 추정
if method == 'Approx LS':
self._fit_approx_ls()
elif method == 'Non-linear LS':
self._fit_nonlinear_ls(tolerance)
elif method == 'YW':
self._fit_yw()
else:
self._fit_mle(tolerance=tolerance,method=method,grad_method=grad_method)
## 2) 모형 적합값 계산
self.fitted_values = self._fitted_values(self.phi,self.mu)
## 3) 백색 잡음 분산 추정량 계산
if method == 'EMLE':
pass
else:
self.error_variance = self._get_error_variance(self.phi,self.mu,method)
## 4) 표준 오차 계산
ev = self.error_variance
auto_cov_matrix = self._auto_cov_matrix()
self.std_error = np.sqrt(ev*np.linalg.inv(auto_cov_matrix)/len(self.data)).squeeze()+0
이제 필요한 함수들을 각각 정의한다. 먼저 적합값을 계산하는 함수를 만든다.
class autoRegressiveModel():
''' 생략 '''
def _fitted_values(self,phi,mu):
## 적합값 계산 함수
data = self.data
p = self.p
y = data[p:] - mu
n = len(data)
X = []
for i in range(n-p):
row = data[i:i+p][::-1]-mu
X.append(row)
X = np.array(X)
return X.dot(phi) + mu
다음으로 백색 잡음 분산을 추정하는 함수를 정의했다.
class autoRegressiveModel():
''' 생략 '''
def _get_error_variance(self,phi,mu,method):
## 백색 잡음 분산 계산
data = self.data
p = self.p
n = len(data)
y = data[p:]
if method == 'YW':
sacf = []
svar = np.var(data)
for k in range(1,p+1):
sacf.append(self.sample_acf(k))
sacf = np.array(sacf)
error_variance = svar-phi.dot(sacf)#### to change
else:
error_variance = np.sum(np.square(y - self._fitted_values(phi,mu)))/(n-p)
return error_variance
최소 제곱법 중에서 근사적인 방법을 이용하여 모수를 추정하는 함수를 구현하였다.
class autoRegressiveModel():
''' 생략 '''
def _fit_approx_ls(self):
data = self.data
p = self.p
n = len(data)
mu = np.mean(data) ## estimate mu
y = data[p:] - mu
X = []
for i in range(n-p):
row = data[i:i+p][::-1]-mu
X.append(row)
X = np.array(X)
X_tX = X.T.dot(X)
X_tX_inv = np.linalg.inv(X_tX)
phi = X_tX_inv.dot(X.T.dot(y))
self.mu = mu
self.phi = phi
self.intercept = mu*(1-np.sum(phi))
비선형 최소 제곱법을 이용하여 모수를 추정하는 함수를 정의한다.
class autoRegressiveModel():
''' 생략 '''
def _fit_nonlinear_ls(self, tolerance):
data = self.data
self._fit_approx_ls()
phi = self.phi
p = self.p
mu = self.mu
n = len(data)
data = self.data
cur_beta = np.insert(phi,0,mu) ## initial parameter vector
f = lambda x, beta : beta[0] + beta[1:].dot(x-beta[0])
y = data[p:]
while True:
delta_ys = []
J = []
for i in range(n-p):
x = data[i:i+p][::-1]
delta_y = y[i] - f(x,cur_beta)
delta_ys.append(delta_y)
J_row = []
for j in range(len(cur_beta)):
if j == 0:
J_element = 1-np.sum(cur_beta[1:])
else:
J_element = x[j-1]-cur_beta[0]
J_row.append(J_element)
J.append(J_row)
J = np.array(J)
delta_ys = np.array(delta_ys)
J_tJ = J.T.dot(J)
J_tJ_inv = np.linalg.inv(J_tJ)
delta_beta = J_tJ_inv.dot(J.T.dot(delta_ys))
next_beta = cur_beta+delta_beta
if np.max((next_beta-cur_beta)/cur_beta) < tolerance:
self.mu = next_beta[0]
self.phi = next_beta[1:]
self.intercept = mu*(1-np.sum(self.phi))
break
else:
cur_beta = next_beta
$k$차 표본 자기 공분산을 계산하는 함수를 정의한다.
class autoRegressiveModel():
''' 생략 '''
def sample_acf(self,k):
data = self.data
mu = np.mean(data)
n = len(data)
data = data - mu
summand = 0
for j in range(k,n):
summand += data[j]*data[j-k]
return summand/n
식 (3-7) (Yule-Walker 방정식)에서 우변에 나타난 행렬을 추정하는 함수를 만들어 준다.
class autoRegressiveModel():
''' 생략 '''
def _auto_cov_matrix(self):
data = self.data
p = self.p
diag_element = np.array([self.sample_acf(0)]*p)
C = np.diag(diag_element) ## sample autocovariace function를 원소로하는 matrix
if p>1:
for i in range(p-1):
for j in range(i+1,p):
C[i][j] = self.sample_acf(j-i)
C[j][i] = self.sample_acf(j-i)
return C
Yule-Walker 방정식을 이용한 모수 추정 함수를 만들었다.
class autoRegressiveModel():
''' 생략 '''
def _fit_yw(self):
data = self.data
p = self.p
acf_vector = np.array([self.sample_acf(k) for k in range(1, p+1)])
C = self._auto_cov_matrix()
C_inv = np.linalg.inv(C)
phi = C_inv.dot(acf_vector)
self.mu = np.mean(data)
self.phi = phi
self.intercept = self.mu*(1-np.sum(phi))
다음으로 최대 우도 추정법을 이용한 모수 추정 함수를 만들었다. 꽤 길다 ㄷㄷ;;
class autoRegressiveModel():
''' 생략 '''
def _fit_mle(self,tolerance,method='CMLE',max_iter=20,grad_method='approx'):
valid_methods = ['CMLE','EMLE']
assert method in valid_methods,\
f'method must be the one of {valid_methods}'
valid_grad = ['approx','exact']
assert grad_method in valid_grad,\
f'method must be the one of {valid_grad}'
self.mle_method = method
data = self.data
p = self.p
n = len(data)
if method == 'CMLE':
self._fit_nonlinear_ls(tolerance)
else:
self._fit_nonlinear_ls(tolerance)
### initial value
cur_phi = self.phi
cur_c = self.intercept
cur_mu = cur_c/(1-np.sum(cur_phi))
cur_est_variance = self._get_error_variance(cur_phi,cur_mu,method=None)
cur_params = np.insert(cur_phi,0,cur_c)
hess = -self._approx_hess(cur_params,\
self._get_log_likelihood,cur_est_variance)
cur_A = np.linalg.inv(hess)
iter_cnt = 1
max_val = -np.infty
while iter_cnt <= max_iter:
### grid search for finding good step size
is_improved = False
step = np.array([1,2,4,8,16])
step = np.concatenate([np.arange(0,1,0.01),step])
if grad_method == 'exact':
grad = self._get_first_derivative_log_likelihood(cur_params,cur_est_variance)
else:
grad = self._approx_fdlh(cur_params,cur_est_variance)
for s in step:
temp_params = cur_params+s*cur_A.dot(grad)
obj_val = self._get_log_likelihood(temp_params,cur_est_variance)
if obj_val > max_val:
is_improved = True
max_val = obj_val
opt_s = s
next_params = cur_params+opt_s*cur_A.dot(grad)
diff_params = next_params - cur_params
diff_params = np.expand_dims(diff_params,axis=1)
next_mu = next_params[0]/(1-np.sum(next_params[1:]))
residuals = data[p:]-self._fitted_values(next_params[1:],next_mu)
next_est_variance = np.sum(np.square(residuals))/n
next_vp = self._get_inverse_vp(next_params[1:])
prior_res = data[:p]-np.array([next_mu]*p)
next_est_variance += prior_res.dot(next_vp.dot(prior_res))/n
if grad_method == 'exact':
next_grad = self._get_first_derivative_log_likelihood(next_params,next_est_variance)
else:
next_grad = self._approx_fdlh(next_params,next_est_variance)
diff_grad = next_grad - grad
diff_grad = np.expand_dims(diff_grad,axis=1)
next_A = cur_A - \
cur_A.dot(diff_grad.dot(diff_grad.T.dot(cur_A)))/(diff_grad.T.dot(cur_A.dot(diff_grad))) \
-diff_params.dot(diff_params.T)/(diff_grad.T.dot(diff_params))
if not is_improved:
self.phi = cur_params[1:]
self.mu = cur_params[0]/(1-np.sum(self.phi))
self.intercept = cur_params[0]
self.log_likelihood = max_val
self.error_variance = cur_est_variance
break
elif np.max(np.abs(diff_params/cur_params)) < tolerance or not self.is_pos_def(next_A):
self.phi = next_params[1:]
self.mu = next_params[0]/(1-np.sum(self.phi))
self.intercept = next_params[0]
self.log_likelihood = max_val
self.error_variance = next_est_variance
break
else:
cur_params = next_params
cur_est_variance = next_est_variance
cur_A = next_A
iter_cnt += 1
최대 우도 추정 방법 사용 시 필요한 함수를 정의하였다. 순서대로 $V_p^{-1}$을 계산하는 함수, 로그 우도 함수의 1차 미분 벡터 계산 함수, 로그 우도 값 계산 함수, 헤시안 행렬 근사 함수, 그라디언트 근사 함수, 로그 우도 함수의 미분 근사 함수, 주어진 행렬이 양정치인지 체크하는 함수, $\partial v_{ij}/\partial \phi_m$ 계산 함수이다.
class autoRegressiveModel():
''' 생략 '''
def _get_inverse_vp(self,phi):
if not isinstance(phi,np.ndarray):
phi = np.array(phi)
p = self.p
assert len(phi) == p, f'order{p} do not equal to length of phi vector({len(phi)})'
inverse_vp = np.zeros((p,p))
for i in range(p):
for j in range(i,p):
first_part_left_phis = np.insert(phi[:i],0,-1)
if i == j:
first_part_right_phis = first_part_left_phis
else:
first_part_right_phis = phi[j-i-1:j]
seconde_part_left_phis = phi[p-j-1:p+i-j]
seconde_part_right_phis = phi[p-i-1:p]
if i == j:
inverse_vp[i][j] = 0.5*(first_part_left_phis.dot(first_part_right_phis) - \
seconde_part_left_phis.dot(seconde_part_right_phis))
else:
inverse_vp[i][j] = first_part_left_phis.dot(first_part_right_phis) - \
seconde_part_left_phis.dot(seconde_part_right_phis)
inverse_vp = inverse_vp+inverse_vp.T ## make symmetric matrix
return inverse_vp
def _get_first_derivative_log_likelihood(self,params,est_variance):
## check
c = params[0]
phi = params[1:]
data = self.data
n = len(data)
p = self.p
inverse_vp = self._get_inverse_vp(phi)
x = data[:p]
mu = c/(1-np.sum(phi))
dmu_dphi = c/np.square((1-np.sum(phi)))
##### calculate dl_dc
dmu_dc = 1/(1-np.sum(phi))
### second part derivative w.r.t c
temp1 = 0
for i in range(p):
for j in range(p):
temp1 += x[i]*inverse_vp[i][j]
dsecond_dc = (dmu_dc*temp1 - mu*dmu_dc*np.sum(inverse_vp))/est_variance
### third part derivative w.r.t c
temp2 = 0
for t in range(p,n):
res = data[t] - c - data[t-p:t][::-1].dot(phi)
temp2 += res
dthird_dc = temp2/est_variance
dl_dc = dsecond_dc + dthird_dc
##### calculate dl_dphi
dl_dphi = []
for m in range(p):
####### term 하나씩 비교해보자 손으로 풀어서
#### first part derivative w.r.t phi[m]
temp3 = np.zeros((p,p))
for i in range(p):
for j in range(i,p):
temp3[i][j] = self.dvp_dphi(phi,m,i,j)
dvp_dphi_matrix = temp3 + temp3.T - \
np.diag(np.diagonal(temp3))
vp = np.linalg.inv(inverse_vp)
dfirst_dphi = 0.5*np.sum(np.diagonal(vp.dot(dvp_dphi_matrix)))
#### second part derivative w.r.t phi[m]
spdp = 2*mu*dmu_dphi*np.sum(inverse_vp) + np.square(mu)*np.sum(dvp_dphi_matrix)
for i in range(p):
for j in range(p):
spdp -= 2*dmu_dphi*x[i]*inverse_vp[i][j] + 2*mu*x[i]*dvp_dphi_matrix[i][j]
spdp += x[i]*x[j]*dvp_dphi_matrix[i][j]
dsecond_dphi = (-0.5)*spdp/est_variance
#### third part derivative w.r.t phi[m]
temp4 = 0
for t in range(p,n):
res = (data[t] - c - data[t-p:t][::-1].dot(phi))*data[t-m-1]
temp4 += res
dthird_dphi = temp4/est_variance
dl_dphi.append(dfirst_dphi+dsecond_dphi+dthird_dphi)
return np.array([dl_dc]+dl_dphi)
def _get_log_likelihood(self,params,est_variance):
c = params[0]
phi = params[1:]
data = self.data
p = self.p
n = len(data)
x = data[:p]
mu = np.array([c/(1-np.sum(phi))]*p)
inverse_vp = self._get_inverse_vp(phi)
# print('in vp', inverse_vp)
# print('mu',mu)
temp = 0
temp += -0.5*n*np.log(2*np.pi*est_variance)
temp += 0.5*np.log(np.linalg.det(inverse_vp))
temp += -0.5*(x-mu).dot(inverse_vp.dot(x-mu))/est_variance
temp2 = 0
for t in range(p,n):
res = data[t] - c - data[t-p:t][::-1].dot(phi)
temp2 += np.square(res)
temp -= 0.5*temp2/est_variance
return temp
def _approx_hess(self,x,func,*args,epsilon=0.001):
m = len(x)
approx_hess_matrix = np.zeros((m,m))
for i in range(m):
for j in range(i,m):
e_i = np.zeros(m)
e_i[i] = 1
e_j = np.zeros(m)
e_j[j] = 1
temp = (0.25/np.square(epsilon))*\
((func(x+epsilon*e_i+epsilon*e_j,*args)-func(x+epsilon*e_i-epsilon*e_j,*args))-\
(func(x-epsilon*e_i+epsilon*e_j,*args)-func(x-epsilon*e_i-epsilon*e_j,*args)))
approx_hess_matrix[i][j] = temp
approx_hess_matrix = approx_hess_matrix + approx_hess_matrix.T -\
np.diag(np.diagonal(approx_hess_matrix))
return approx_hess_matrix
def _approx_grad(self,x,func,*args,epsilon=0.000001):
temp = []
for i in range(len(x)):
e = np.zeros(len(x))
e[i] = 1
diff = (func(x+epsilon*e,*args) - func(x,*args))/epsilon
temp.append(diff)
return np.array(temp)
def _approx_fdlh(self,x,*args):
return self._approx_grad(x,self._get_log_likelihood,*args)
def is_pos_def(self,x):
return np.all(np.linalg.eigvals(x) > 0)
def dvp_dphi(self,phi,m,i,j):
p = self.p
temp = 0
if i==j:
if i >= 1:
if m <= i-1:
temp += 2*phi[m]
if m >= p-j-1 and m <= p-1:
temp -= 2*phi[m]
elif i<j:
if i >= 1:
if m <= i-1:
temp += phi[m+j-i]
if m >= j-i-1 and m <= j-1:
if m-j+i < 0:
temp -= 1
else:
temp += phi[m-j+i]
if m >= p-j-1 and m <= p+i-j-1:
temp -= phi[m+j-i]
if m >= p-i-1 and m <= p-1:
temp -= phi[m-j+i]
return temp4. 예측(Forecasting)
예측은 시계열 분석에서 사람들이 가장 관심 있어하는 부분이라고 생각한다.
AR($p$) 모형을 따르는 정상성 시계열 $X_t, \;t=1, 2, \ldots, n$이 있다고 했을 때 미래의 $n+k$ 시점의 예측값과 예측 구간을 계산해보자.
1) 예측값
$I_n = (X_1, X_2, \ldots, X_n)$라 하자. 먼저 $n$시점까지의 시계열 데이터가 주어졌을 때 $n+k$ 시점의 예측값 $X_{n+k, n}$은 다음과 같이 예측 오차 제곱을 최소화하는 것으로 한다.
$$E(X_{n+k}-f(I_n))^2$$
계산해보면 예측 오차 제곱 최소화하는 것은 $E(X_{n+k}|I_n)$인 것을 알 수 있다. 즉, $X_{n+k,n}=E(X_{n+k}|I_n)$이다.
$X_{n+1,n}$을 구해보자.
$$\begin{align}X_{n+1,n} &=E(X_{n+1}|I_n) \\ &=c + \phi_1 E(X_n|I_n) + \cdots +\phi_p E(X_{n-p+1}|I_n) + E(Z_{n+1}|I_n) \\ &= c + \phi_1 X_n + \cdots + \phi_p X_{n-p+1} \end{align}$$
세 번째 등식에서 $X_k \in I_n, \;k=n-p+1, \ldots, n$인 경우 $E(X_k|I_n) = X_k$이고 $Z_{n+1}$은 $I_n$과 독립이기 때문에 $E(Z_{n+1}|I_n)=E(Z_{n+1})=0$이다. 이런 식으로 $n+k$ 시점에서 예측값을 다음과 같이 추정할 수 있다.
$$\begin{align}X_{n+k,n} &= c+\phi_1E(X_{n+k-1}|I_n) + \cdots + E(X_{n+k-p}|I_n) +E(Z_{n+k}|I_n) \\ &= c+\phi_1E(X_{n+k-1}|I_n) + \cdots + E(X_{n+k-p}|I_n) \end{align}$$
여기서
$$ E(X_{n+i}|I_n) = \begin{cases}&X_{n+i} \text{ for } i \leq 0 \\ &X_{n+i, n} \text{ for } i > 0 \end{cases}$$
실제로 예측할 때에는 $\phi_j,\;(j=1, \ldots, p)$ 대신 우리가 추정한 $\hat{\phi}_j$를 사용한다.
2) 예측 구간
예측 구간을 구하기 위해서는 $n+k$ 시점에서의 예측 오차의 분산 $\text{var}(e_{n+k,n})$을 구해야 한다. 여기서 $e_{n+k,n} = X_{n+k}-X_{n+k,n} = X_{n+k}-E(X_{n+k}|I_n)$이다. $\text{var}(e_{n+1,n})$을 구해보자.
$$\begin{align}\text{var}(e_{n+1,n}) &= E(X_{n+1}-X_{n+1,n})^2 \\ &= E(c+\phi_1X_{n} + \cdots + \phi_pX_{n-p+1}+Z_{n+1} - c - \phi_1 X_n - \cdots - \phi_p X_{n-p+1})^2 \\ &= E(Z_{n+1}^2) = \sigma^2 \end{align}$$
$\text{var}(e_{n+k,n})$도 순차적으로 계산할 수 있다. 예측 오차의 분산을 추정할 때에는 백색 잡음의 분산 추정값 $\hat{\sigma}^2$을 이용한다.
예측 구간을 계산할 때에는 정규분포의 꼬리값을 이용한다. 따라서 $n+k$ 시점에서의 $(1-\alpha)$% 예측 구간은 다음과 같다.
$$E(X_{n+k}|I_n) \pm z_{\alpha/2}\sqrt{\text{var}(e_{n+k,n})}$$
3) 파이썬 코드
예측을 위한 함수도 추가해주자. 먼저 $n+1$ 부터 $n+k$ 시점까지 예측값을 계산해주는 함수를 만든다. 이 함수는 개별 시점에서의 예측값을 계산하는 함수를 불러온다.
class autoRegressiveModel():
''' 생략 '''
def predict(self,k):
assert k > 0, 'k must be positive integer'
c = self.intercept
phi = self.phi
data = self.data
data = data[::-1]
return np.array([self._predict(j,c,phi,data) for j in range(1,k+1)])
다음으로 개별 시점에서의 예측값을 구하는 함수를 정의한다. 예측값은 재귀식으로 구성되어 있으며 인덱스가 $n$ 보다 작거나 같은 경우, 그리고 $n$보다 큰 경우 다르게 처리해줘야 하는 것을 주목하자.
class autoRegressiveModel():
''' 생략 '''
def _predict(self,k,c,phi,data):
global predict_value
predict_value = c
p = len(phi)
for j in range(p):
if k-j-1<=0:
predict_value += phi[j]*data[1+j-k]
else:
predict_value += phi[j]*self._predict(k-j-1,c,phi,data)
return predict_value
다음은 예측 구간을 구하는 코드를 만들어보자. 먼저 예측 분산을 계산하는 함수를 예측값을 구하는 방식과 비슷한 방법으로 계산한다.
class autoRegressiveModel():
''' 생략 '''
def _prediction_variances(self,k):
assert k > 0, 'k must be positive integer'
phi = self.phi
error_variance = self.error_variance
return np.array([self._prediction_variance(j,error_variance,phi) for j in range(1,k+1)])
def _prediction_variance(self,k,error_variance,phi):
global prediction_variance
prediction_variance = error_variance
p = len(phi)
for j in range(p):
if k-j-1<=0:
pass
else:
prediction_variance += np.square(phi[j])*\
self._prediction_variance(k-j-1,error_variance,phi)
return prediction_variance
예측 구간을 구해주는 함수를 만들자!
class autoRegressiveModel():
''' 생략 '''
def predict_interval(self,k,alpha=0.05):
upper_limits = []
lower_limits = []
for j in range(1,k+1):
limit = self._predict_interval(j,alpha)
upper_limits.append(limit[1])
lower_limits.append(limit[0])
return lower_limits, upper_limits
def _predict_interval(self,k,alpha):
c = self.intercept
phi = self.phi
data = self.data
data = data[::-1]
error_variance = self.error_variance
pred = self._predict(k,c,phi,data)
pv = self._prediction_variance(k,error_variance,phi)
upper_limit = pred+norm.ppf(1-alpha/2)*np.sqrt(pv)
lower_limit = pred-norm.ppf(1-alpha/2)*np.sqrt(pv)
return lower_limit, upper_limit
드뎌 끝났다!!
5. 예제
여기서 다룰 데이터를 다운받아주자.
당연한 얘기겠지만 데이터를 다운받았으면 불러오자 ㅎㅎ;;
df = pd.read_csv('./dataset/color_property.csv')
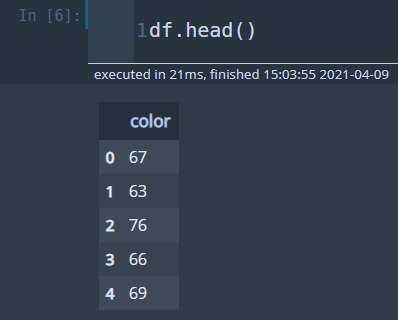
나는 AR(1) 모형을 적합하려고 한다. 데이터를 Numpy 배열로 바꿔준다.
data = df['color'].values
그리고 내가 만든 autoRegressiveModel 인스턴스를 하나 만들어준다. 이때 데이터와 차수 $p$를 인자로 넣어준다.
ar_1 = autoRegressiveModel(data,1)
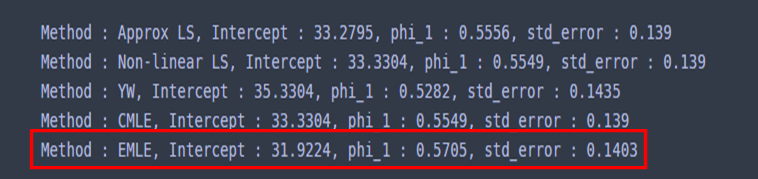
모형 추정 방법별로 결과가 어떤지 확인해보고자 한다.
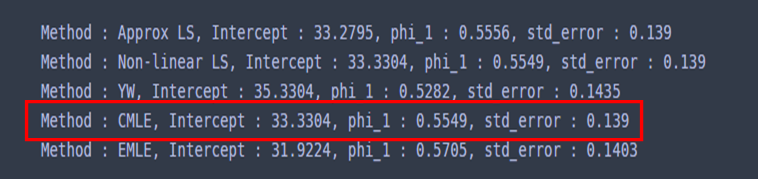
for m in ['Approx LS','Non-linear LS','YW','CMLE','EMLE']:
ar_1.fit(method=m)
res_str = f'Method : {m}, '
res_str += f'Intercept : {round(ar_1.intercept,4)}, '
for i, p in enumerate(ar_1.phi):
res_str += f'phi_{i+1} : {round(p,4)}, '
res_str += f'std_error : {round(ar_1.std_error,4)} '
print(res_str)

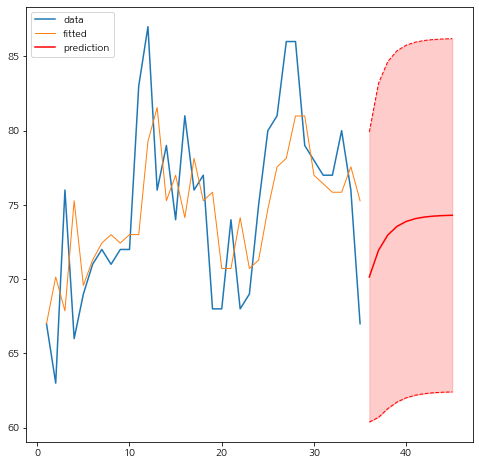
각 방법별로 조금씩 차이가 있다. 당연한 것이다. 이제 예측 구간을 그려보려고 한다. 나는 미래 10 시점까지의 예측값과 예측 구간을 그려봤다.
data = df['color'].values
ar_1 = autoRegressiveModel(data,1)
ar_1.fit(method='EMLE')
fitted_values = ar_1.fitted_values
fitted_values = np.insert(fitted_values,0,data[0]) ## 적합값
k = 10 ## 예측하고자할 예측 시점
pred = ar_1.predict(k)
pred_interval = ar_1.predict_interval(k)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
x = range(1,len(data)+1)
plt.plot(x,data,label='data')
plt.plot(x,fitted_values,label='fitted',linewidth=1)
## prediction, prediction interval
pred_x = range(len(data)+1,len(data)+k+1)
plt.plot(pred_x,pred,color='purple',label='prediction')
plt.plot(pred_x,pred_interval[0],color='purple',linestyle='--',linewidth=1)
plt.plot(pred_x,pred_interval[1],color='purple',linestyle='--',linewidth=1)
plt.fill_between(pred_x,pred_interval[0],pred_interval[1],color='purple',alpha=0.2)
plt.plot()
plt.legend()
plt.show()
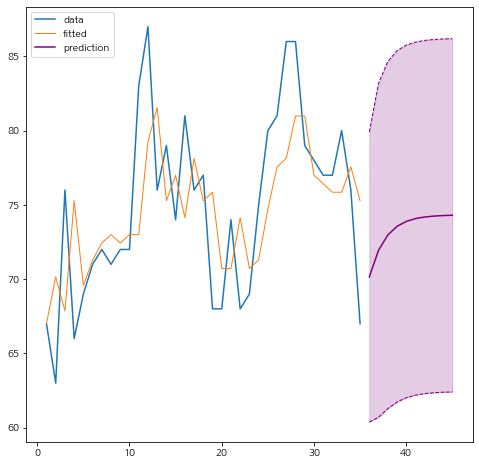
예쁘게 잘 나왔다. 나는 내가 구현한 것과 statsmodel의 결과를 비교해보려고 한다. 추가적인 모듈을 임포트 한다.
import statsmodels.api as sm
import warnings
warnings.simplefilter(action='ignore', category=FutureWarning)
from scipy.stats import norm
from statsmodels.tsa.ar_model import AutoReg
from statsmodels.tsa.ar_model import AR
먼저 Conditional MLE(Least Square는 Conditional MLE와 같다는 것을 기억하자)를 구해주는 코드는 다음과 같다.
fit = AutoReg(data,1).fit()
fit.summary()
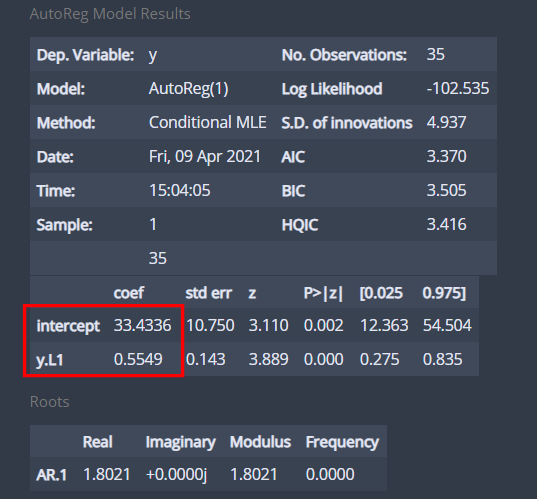
내가 구현한 결과와 비교해보면 절편항과 모수 $\phi_1$의 표준오차에는 약간 차이가 나지만 모수의 추정치는 거의 일치했다.
이번엔 Yule-Walker를 이용한 모수를 추정해보자. 아래 코드는 모수와 백색 잡음의 분산을 추정한다.
rho, sigma = sm.regression.yule_walker(data, order=1, method='mle')
print(f'phi : {rho[0]}, wn_variance : {sigma}')

다음은 내가 구현한 코드를 이용하여 모수와 백색 잡음의 분산을 추정해보았다.
ar_1 = autoRegressiveModel(data,1)
ar_1.fit(method='YW')
print(f'phi : {ar_1.phi[0]}, wn_variance : {np.sqrt(ar_1.error_variance)}')

정확히 일치했다.
마지막으로 Unconditional MLE를 이용해보자.
fit = AR(data).fit(maxlag=1,method='mle',trend='c')
fit.summary()
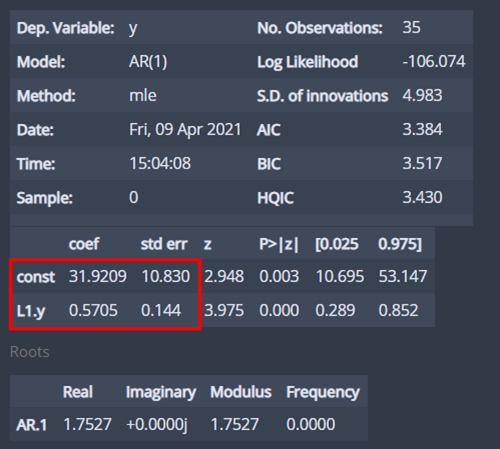
내가 구현한 결과와 비교해보면 절편항과 모수 $\phi_1$의 표준오차에는 약간 차이가 나지만 모수의 추정치는 거의 일치했다.
이번에는 statsmodels를 이용하여 미래 10 시점까지의 예측값과 예측 구간을 시각화해보자. statsmodels를 이용하여 예측값, 예측 구간은 아래의 두 가지 방법 중에 하나를 선택하면 된다.
k = 10
alpha = 0.05
pred = fit.predict(start=len(data),end=len(data)+k-1,dynamic=False)
lower_limit = pred - norm.ppf(1-alpha/2)*np.sqrt(fit.sigma2)
upper_limit = pred + norm.ppf(1-alpha/2)*np.sqrt(fit.sigma2)
또는
k = 10
arma_res = sm.tsa.ARMA(data, order=(1,0)).fit()
pred, _, cl = arma_res.forecast(k)
lower_limit = [x[0] for x in cl]
upper_limit = [x[1] for x in cl]
아래는 시각화 코드이다. 앞서 살펴보았던 것과 거의 흡사하다.
fitted_values = fit.fittedvalues
fitted_values[0] = data[0] ## 적합값
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
x = range(1,len(data)+1)
plt.plot(x,data,label='data')
plt.plot(x,fitted_values,label='fitted',linewidth=1)
## prediction, prediction interval
pred_x = range(len(data)+1,len(data)+k+1)
plt.plot(pred_x,pred,color='red',label='prediction')
plt.plot(pred_x,lower_limit,color='red',linestyle='--',linewidth=1)
plt.plot(pred_x,upper_limit,color='red',linestyle='--',linewidth=1)
plt.fill_between(pred_x,lower_limit,upper_limit,color='red',alpha=0.2)
plt.plot()
plt.legend()
plt.show()
아래는 내가 구현한 것(왼쪽)과 statsmodels를 이용한 것(오른쪽)을 비교해보자.
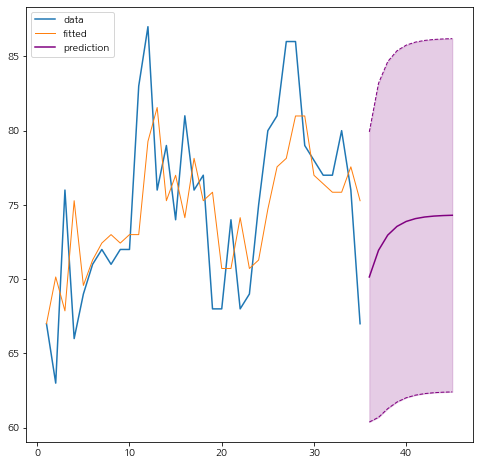

비교해보면 결과가 동일한 것을 알 수 있다.
6. 장단점
- 장점 -
선형 모형이므로 계산이 쉽고 자기 상관성을 보이는 데이터의 추세를 시각적으로 파악하는데 도움이 된다. 또한 모수 추정량에 대한 이론적인 성질(점근 정규성)이 많이 알려져 있다.
- 단점 -
실제 시계열은 비선형적으로 움직이는 매우 복잡한 패턴을 가지고 있다. 따라서 선형 모형으로 적합하는 것은 과소 적합을 야기할 수 있다. 또한 해당 시계열에 영향을 미치는 설명 변수를 사용하지 않아 변수 간 상관관계를 파악하는 데에는 자기 회귀 모형이 적합하지 않다.
마치며
여기서 질문을 할 수 있다.
데이터를 보고 차수 $p$를 어떻게 선택해야 하는가?
이는 시각적으로 확인하거나 여러 통계량을 보고 결정할 수 있는데 이에 대한 내용은 추후 포스팅에서 다루겠다(아마도 ARMA 또는 ARIMA 모델을 다룬후 소개할 것 같다).
원래는 1주일 적어도 하나의 포스팅을 올리려고 했으나 양이 방대해져 시간이 오래 걸렸다. 나의 똥고집인지는 모르겠지만 나는 알고리즘을 이해했으면 직접 구현해봐야 속이 후련한 스타일이라서 구현하는 데 시간이 걸렸다. 또한 구현한 것을 공식적으로 사용하고 있는 statsmodels와 비교해보는 것도 시간이 걸렸고 수식을 입력하는 것도 꽤나 힘들었다 ㅠ.ㅠ. 물론 회사 생활하느라 블로그에 시간을 많이 투자하지 못한 것도 있다. 그래도 직접 구현해보는 것 덕분에 기억이 오래가고 결과도 일치해서 기분이 좋았다. 하지만 효율성을 생각하면 그냥 구현은 패스하고 있는 걸 잘 써보려고 한다. 구현은 내가 내킬 때 해야지 ㅎㅎ;;
참고자료
위키백과 - Autoregressive Model
Cryer - Time Series Analysis with Application in R
Hamilton, J.D. - Time Series Analysis
Shumway, R.H. and Stoffer, D.S. - Time Series Analysis and its Applications

'통계 > 시계열 모형' 카테고리의 다른 글
| [시계열 분석] 6. 이동 평균 모형(Moving Average Model) 적합하기 with Python (809) | 2021.08.20 |
|---|---|
| [시계열 분석] 5. 자기 상관 함수(Autocorrelation Function : ACF)과 부분 자기 상관 함수(Partial Autocorrelation : PACF) with Python (1038) | 2021.07.31 |
| [시계열 분석] 3. (General) Durbin-Watson 검정 with Python (1118) | 2021.03.21 |
| [시계열 분석] 2. 최소 제곱법을 이용한 시계열 분석 with Python (1) | 2021.02.24 |
| [시계열 분석] 1. 시계열 데이터와 정상 과정(Stationary Process) (2) | 2021.02.21 |





댓글