이번 포스팅에서는 인접 모형(Nested)들을 적합도 측면에서 비교하는 방법과 모형 적합이 실제로 잘되었는지 확인해보는 방법에 대해서 소개하려고 한다. 이 포스팅을 읽기 전에 아래의 내용을 읽어보고 오기 바란다.
- Exponential Dispersion Family
여기서 다루는 내용은 다음과 같다.
1. Deviance와 Generalized Pearson 통계량
1. Deviance와 Generalized Pearson 통계량
$y_i$의 확률 분포는 exponential dispersion family라고 하자. 같은 분포에서 독립적으로 관측된 반응 변수 벡터를 $y = (y_1, \ldots, y_n)^t$, 평균 벡터 $\mu = (\mu_1, \ldots, \mu_n)$으로 표현된 $y$의 로그 우도 함수를 $L(\mu; y)$라 하자. 여기서 $\mu_i=E(y_i)$이다. 이때 $\mu$의 최대 우도 추정량을 $\hat{\mu}$라고 하자.
특별히 $\hat{\mu} = y$인 경우 해당 모형을 saturated 모형이라고 한다. 즉, saturated 모형은 설명 변수를 무시하고 무조건 반응 변수 값으로 $E(y_i)$를 추정한다는 것이며 가장 완벽한 적합도를 갖는 모형이다.
- Deviance -
먼저 $\hat{\mu}$가 주어진 상황에서 natural parameter $\theta_i$의 최대 우도 추정량을 $\hat{\theta}_i$라 하자(연결 함수 $g$에 대하여 $\theta_i=g(\mu)$임을 상기하자). 그리고 $\tilde{\theta}_i$를 satureated 모형에 대한 $\theta_i$의 추정량이라고 하자. 이제 다음의 로그 우도비를 고려하자.
$$\begin{align}-2[L(\hat{\mu}; y) - L(y; y)] &= 2\sum_{i=1}^n[y_i\tilde{\theta}_i-b(\tilde{\theta}_i)]/a(\phi)-2\sum_{i=1}^n[y_i\hat{\theta}_i-b(\hat{\theta}_i)]/a(\phi)\\ &= 2\sum_{i=1}^nw_i[y_i(\tilde{\theta}_i-\hat{\theta}_i)-b(\tilde{\theta}_i)+b(\hat{\theta}_i)]/\phi \\ &= D(y; \hat{\mu})/\phi\end{align}\tag{1}$$
여기서 $a(\phi)=\phi/w_i$이다. 이때 $D(\hat{\mu}; y)/\phi$를 ScaledDeviance, $D(\hat{\mu}; y)$을 Deviance 라고 한다.
$y_i$는 exponential dispersion family를 따르므로 $\hat{\mu}=y$일때 $L$은 최대값을 가진다.
$$\begin{align}\because L(\mu; y) &= \sum_{i=1}^n\left\{[y_i\theta_i-b(\theta_i)]/a(\phi)+c(y_i, \phi)\right\}\\ & \Longrightarrow \frac{\partial L}{\partial \mu_i} = \left[y_i\frac{\partial \theta_i}{\partial \mu_i}-b'(\theta_i)\frac{\partial \theta_i}{\partial \mu_i}\right]/a(\phi) =\left[y_i\frac{\partial \theta_i}{\partial \mu_i}-\mu_i\frac{\partial \theta_i}{\partial \mu_i}\right]/a(\phi) = 0 \\ &\Longrightarrow \mu_i=y_i \end{align}$$
따라서 $L(\hat{\mu};y) \leq L(y; y)$이며 따라서 $D(\hat{\mu}; y)\geq 0$이 된다.
눈치챈 사람도 있겠지만 Deviance값이 클수록 모형 적합이 잘 안되었다는 뜻이다. 따라서 Deviance는 모형 적합 정도를 측정하는 측도라고 할 수 있다. Scale Deviance의 경우 주어진 모형의 파라미터 개수가 $p+1$이라고 할 때 특정 조건하에서 자유도가 $n-(p+1)$인 카이제곱 분포를 근사적으로 따른다고 한다. 따라서 Scale Deviance를 이용하면 모형 적합 정도를 통계적으로 검정할 수 있다.
Deviance는 모형 적합 정도를 측정하는 측도라고 하였다. 따라서 모형의 비교를 위해 Deviance를 사용할 수 있다.
- Deviance 예 -
(1) $y_i\sim \text{Poisson}(\mu_i)$인 경우
$$L(\mu; y) = \sum_{i=1}^n[y_i\log{\mu_i}-\mu_i-y_i!] \Longrightarrow D(y; \hat{\mu}) = 2\sum_{i=1}^n\left(y_i\log{\frac{y_i}{\hat{\mu}_i}}-y_i+\hat{\mu_i}\right)$$
(2) $y_i\sim N(\mu_i,\sigma^2)$, $\sigma^2$은 알고 있다고 가정
$$L(\mu; y) = \sum_{i=1}^n\left[\frac{y_i\mu_i - \frac{1}{2}\mu_i^2}{\sigma^2}-\frac{1}{2}\log (2\pi\sigma^2)-\frac{y_i^2}{2\sigma^2}\right]\Longrightarrow D(y;\hat{\mu}) = \sum_{i=1}^n(y_i-\hat{\mu}_i)^2$$
- Generalized Peason Statistics -
$\phi=1$인 경우 $\text{var}(y_i) = v(\mu_i)$라 하고 주어진 모형에 대한 다음의 통계량을 고려해보자.
$$X^2 = \sum_{i=1}^n\frac{(y_i-\hat{\mu}_i)^2}{v(\hat{\mu}_i)}$$
이때 $X^2$를 Generalized Pearson(GP) 통계량이라고 한다. GP 통계량 또한 모형의 적합 정도를 측정하는 측도로 활용될 수 있다.
- Deviance vs GP 통계량
반응 변수 $y_i$가 정규분포를 따르는 경우 다시 말해서 $y_i\sim N(\mu_i, \sigma^2)$인 경우 $\phi = \sigma^2$라 할 때, $X^2/\phi = D(\hat{\mu};y)/\phi$와 같다. 즉, Deviance와 GP 통계량의 Scaled 버전은 정확히 일치하게 된다.
정규분포가 아니면 일반적으로 Deviance와 GP 통계량 값은 달라진다. 이때 모형 비교를 위한 측도로써 어떤 것을 써야 하는가에 대한 질문이 나올 수 있다. Deviance는 그 차이를 이용하여 Nested 모형에 대하여 일반적인 로그 우도비 검정을 수행할 수 있게 하고, Additive한 성질이 있다. GP 통계량은 Nested 모형을 비교하기 위한 용도로 사용할 수 없다.
(Additive한 성질의 의미는 아래에서 설명한다)
GLM의 적합성은 잔차 분석을 통해서 알 수 있는데 Deviance를 이용한 잔차와 GP 통계량을 이용한 잔차가 있다. 이때 잔차를 이용하여 정규 분포 q-q 그림을 그려보고 일직선에 가까우면 해당 시각적으로 GLM의 적절성을 판단할 수 있다. 이때 반응 변수의 분포가 정규 분포가 아니라 하더라도 Deviance를 이용한 잔차가 정규 분포를 잘 근사한다고 알려져 있다. 따라서 잔차 분석 시에는 GP 통계량보다는 Deviance를 이용하자.
2. 모형 비교
$M_0$를 파라미터 개수가 $p_0$인 모형, $M_1$를 파라미터 개수가 $p_1$인 모형이라고 하자. 이때 $M_0 \subset M_1$인 경우, 다시 말하면 $M_0$이 $M_1$의 특수한 케이스인 경우 $M_0$, $M_1$를 인접 모형(Nested Model) 관계에 있다고 한다.
여기서는 $M_1$이 $M_0$ 보다 더 좋은 모형인지 아닌지를 통계적으로 검정하는 방법에 대해서 알아본다. 즉, 검정하고자 하는 것은 다음과 같다.
$$H_0 : M_0 \text{ holds} \;\;\text{vs} \;\;\; H_1 : M_1 \text{ holds}$$
$\hat{\mu}_0$를 $M_0$를 이용한 적합값, $\hat{\mu}_1$을 $M_1$을 이용한 적합값이라고 하자. $M_0 \subset M_1$이므로 $L(\hat{\mu}_0; y)\leq L(\hat{\mu}_1)$이다. 이를 통해 다음을 알 수 있다.
$$D(y; \hat{\mu}_1) \leq D(y;\hat{\mu}_0)$$
즉, $M_1$에 대한 Deviance 값이 무조건 작으며 적합 측면에서는 $M_1$이 항상 좋게 나온다. 따라서 단순히 $D$ 값이 높고 낮음을 이용하여 모형이 좋고 안 좋음을 비교하는 것은 의미가 없다. 이 경우 Deviance의 차이를 이용하여 $M_1$이 $M_0$보다 적합 정도의 차이가 유의미하게 좋은지를 보아야 할 것이다.
$$-2[L(\hat{\mu}_0;y)-L(\hat{\mu}_1)] = D(y; \hat{\mu}_0) - D(y; \hat{\mu}_1) := \chi^2\tag{2}$$
식 (2)이 의미하는 것은 Deviance의 차이는 로그 우도 값의 차이이며 이는 카이 제곱 분포를 통하여 $H_0$에 대한 검정을 할 수 있다는 것을 의미한다(식 (1)의 좌변은 로그 우도비 검정 통계량이다).
적절한 조건하에서 식 (1)의 좌변은 근사적으로 자유도가 $p_1-p_0$인 카이 제곱 분포를 따른다는 사실이 알려져 있다(적절한 조건이 궁금한 사람은 여기에서 12쪽을 참고하기 바란다).
$\chi^2_{\alpha}(p_1-p_0)$을 자유도가 $p_1-p_0$인 카이 제곱 분포에서 오른쪽 꼬리 확률이 $\alpha$가 되게 하는 값이라고 할 때 $\chi^2>\chi^2_{\alpha}(p_1-p_0)$이면 $H_0$를 기각한다.
※ Deviance의 Additive 성질
식 (1)의 우변을 $M_1$에 대한 $M_0$의 검정 통계량이라는 의미로 $T_{M_0|M_1}$이라 하자.
$M_0\subset M_1 \subset M_2$인 모형 $M_1, M_2, M_3$가 있다고 하자. Deviance는 다음과 같은 성질이 있다.
$$T_{M_0|M_2} = T_{M_0|M_1} + T_{M_1|M_2}$$
이러한 성질을 Deviance의 Additive한 성질이라고 한다. 이게 좋은 이유는 2개를 알면 나머지 하나는 자동적으로 알 수 있어 검정을 좀 더 쉽게 할 수 있기 때문이다. 여기서는 모형 3개에 대하여 전개하였지만 더 확장 가능하다.
3. 시각적으로 모형 적합 확인
- Pearson 잔차 -
Pearson 잔차 $e_i$는 다음과 같이 정의된다.
$$e_i=\frac{y_i-\hat{\mu}_i}{\sqrt{v(\hat{\mu}_i)}}$$
여기서 $v(\mu)=\text{var}(y_i)$이다.
- Deviance 잔차 -
식 (1)에서 $d_i$를 다음과 같이 정의하자.
$$d_i = 2w_i[y_i(\tilde{\theta}_i-\hat{\theta}_i)-b(\tilde{\theta}_i)+b(\hat{\theta}_i)]$$
이때 Deviance 잔차 $DEV_i$는 다음과 같이 정의한다.
$$DEV_i = \sqrt{d_i}\times \text{sign}(y_i-\hat{\mu}_i)$$
- Standardized 잔차 -
$\eta_i=g(\mu_i)$, $W$를 $i$ 번째 대각 원소가 $(\partial \mu_i/\partial \eta_i)^2/\text{var}(y_i)$인 대각 행렬이라 할 때 $H_w$를 다음과 같이 정의하자.
$$H_w = W^{1/2}X(X^tWX)^{-1}X^tW^{1/2}$$
이때 $H_w$의 $i$번째 대각 원소를 $h_{ii}$라 하자. GLM에서 Standardized Pearson 잔차 $r_i^P$는 다음과 같이 정의한다.
$$r_i^P = \frac{y_i-\hat{\mu}_i}{\sqrt{\hat{\phi}v(\hat{\mu})(1-h_{ii})}}$$
그리고 Standardized Deviance 잔차 $r_i^D$는 다음과 같이 정의한다.
$$r_i^D = \frac{DEV_i}{\sqrt{\hat{\phi}(1-h_{ii})}}$$
- 모형 적합 확인 -
앞에서 여러 가지 잔차를 소개하였지만 McCullagh와 Nelder는 모형 적합 확인을 위한 잔차로 Standardized Deviance 잔차를 사용하라고 권장하고 있다.
회귀 분석에서 모형의 적합성을 확인하기 위해 잔차도를 그려보는 것처럼 일반화 선형 모형에서도 잔차도를 활용할 수 있다. 적합값 $\hat{\mu}$에 대하여 앞서 소개한 잔차를 그려본다. 이때 잔차가 0 근방에서 대칭적으로 분포하고 변동이 일정하다면 모형은 잘 적합된 것으로 판단한다.
또한 적합을 분산 안정 변환을 시킨 것으로 대체하여 그려볼 수도 있다. 분산 안정 변환을 $f$라 하면 $f(\hat{\mu})$에 대하여 잔차를 그려본다. 분산 안정 변환은 어떤 GLM을 쓰느냐에 따라 달라지는데 대표적인 것들은 다음과 같다.
$$\begin{align} f(x) = x & \;\; \text{ for Normal GLM} \\ f(x) = 2\sqrt{x} & \;\;\text{ for Poisson GLM} \\ f(x)=2\sin^{-1}\sqrt{x} & \;\;\text{ for binomial GLM} \\ f(x)=2\log{x} & \;\;\text{ for gamma GLM} \\ f(x) = 2x^{-1/2} & \;\;\text{ for inverse Gaussian GLM}\end{align}$$
GLM에서 (특히 Quasi Likelihood를 이용하여 모형을 적합하는 경우) 분산 함수$v(\mu)$와 연결 함수 $g$를 선택하게 된다. 이때 잔차를 통하여 분산 함수와 연결 함수가 제대로 설정된 것인지 아닌지 시각적으로 확인할 수 있는 방법이 있다. Quasi Likelihood를 이용한 모형 적합 방법은 추후 포스팅하겠다.
1) 분산 함수 확인
적합값 또는 분산 안정 변환 적합값에 대하여 잔차의 절대값을 그려본다. 어떠한 패턴도 보이지 않는다면 분산 함수를 제대로 설정했다고 볼 수 있다. 만약 적합값에 대하여 전차의 절대값이 증가하는 패턴을 보인 상황에서 현재 분산을 $v(\mu) = \mu$으로 설정했다면 $v(\mu) = \mu^2$으로 바꿔 본다. 만약 감소하는 패턴을 보이는 상황에서 $v(\mu) = \mu^2$으로 설정했다면 $v(\mu) = \mu$으로 바꿔 본다
2) 연결 함수 확인
일반화 선형 모형 적합은 일반적으로 Iterative Reweighted Least Square(IRLS)를 이용한다. 이때 IRLS 마지막 스텝에서 $z_i$를 다음과 같다고 하자.
$$z_i = \eta_i' + (y_i - \mu_i')\frac{\partial \eta_i'}{\partial \mu_i'}$$
여기서 마지막 스텝에서의 $\beta$ 추정값을 $\beta'$이라 했을 때 $\eta_i' = \tilde{x}_i^t\beta'$, $\mu_i'=g^{-1}(\eta_i')$ 이다.
이때 $\eta_i'$에 대하여 $z_i$를 그려본다. 만약 직선 형태의 패턴이 나온다면 연결 함수가 제대로 설정되었다고 판단할 수 있다. 참고로 $z_i$를 Adjusted Response, $z_i-\eta_i'$를 Working Residual이라고 한다.
McCullagh, Nelder는 연결 함수를 파라미터 $\lambda$에 의존하는 다음과 같은 family를 고려하였다.
$$g(x;\lambda) = \begin{cases} \frac{x^{\lambda}-1}{\lambda}, &\text{ if } \lambda\neq 0 \\ \log{x} & \text{ o.w}\end{cases}$$
McCullagh, Nelder는 만약 위 그림에서 위로 볼록한 형태가 나온다면 현재 사용하고 있는 연결 함수보다 더 낮은 $\lambda$를 고려하고 아래로 볼록한 형태가 나온다면 현재 사용하고 있는 연결함수보다 더 높은 $\lambda$를 고려해보라고 한다.
4. 실제 데이터 적용
이제 실제 데이터를 이용하여 모형도 비교해보고 모형 적합 확인도 해보자. 데이터를 다운받아준다.
필요한 모듈을 임포트한다.
import numpy as np
import statsmodels.api as sm
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels
from functools import reduce
from scipy.stats import chi2
from statsmodels.genmod.generalized_linear_model import GLM
from statsmodels.genmod.families import Poisson
from statsmodels.nonparametric.smoothers_lowess import lowess
범주형 변수를 더미 변수로 변환해주는 함수를 정의한다.
def get_dummy(df,columns,base_value=None):
'''
df : 데이터프레임
columns : 가변수로 변환할 칼럼들
base_value : {가변수로 변환할 칼럼명 : 제외시킬 범주}
'''
for c in columns:
num_level = len(set(df[c])) ## 유니크한 원소의 개수
uniq_element = sorted(list(set(df[c])))[1:] ## 정렬했을 때 첫 번째 범주를 제외
if base_value: ## 제외시킬 범주가 있을 경우 해당 범주를 제외
if c in base_value.keys():
assert base_value[c] in list(set(df[c])), f'{base_value[c]} is not contained in {c}'
uniq_element = sorted(list(set(df[c])-{base_value[c]}))
data = dict()
for i in range(num_level-1):
dummy_data = []
val = uniq_element[i]
for d in df[c]: ## 해당 범주인 경우만 1 나머지는 0
if d == val:
dummy_data.append(1)
else:
dummy_data.append(0)
col_name = c+'_'+str(val) ## 갸변수의 칼럼명 지정
data[col_name] = dummy_data
temp_df = pd.DataFrame(data)
df = pd.concat([df,temp_df],axis=1) ## 가변수 칼럼을 원 데이터 뒤에 결합
return df.drop(columns=columns) ## 원 범주 칼럼은 제외
데이터를 불러온다.
df = pd.read_csv('risky_behaviiors.csv')
범주형 변수를 더미 변수로 바꿔주고 bupacts에 대해서는 로그 변환을 시켜준다. 또한 상수 열도 추가했다.
df = get_dummy(df,['sex','bs_hiv'],{'sex':'woman'}) ## 범주화
df['bupacts'] = df['bupacts'].map(lambda x : np.log(x+1))
df = sm.add_constant(df)
그리고 반응 변수에 해당하는 열 이름과 나머지 열을 설명 변수 열로 지정했다.
y_column = 'fupacts'
x_columns = list(df.columns)
x_columns.remove(y_column)
반응 변수가 횟수이므로 Poisson GLM을 적합시켜준다. 코드 설명은 이전 포스팅과 흡사하므로 여기를 참고하기 바란다.
y = df['fupacts']
X = np.array(df[x_columns])
## initial beta
y_mean = y.mean()*np.ones(len(y))
X_tX = np.matmul(X.T,X)
X_tX_inv = np.linalg.inv(X_tX)
beta = reduce(np.dot,[X_tX_inv, X.T, np.log(y_mean)])
epsilon = 0.0001 ## tolerance
max_iter = 100
iter_count = 0
while iter_count <= max_iter:
iter_count += 1
eta = np.matmul(X,beta)
mu = np.exp(eta)
D = np.diag(mu)
D_inv = np.linalg.inv(D)
z = eta + np.matmul(D_inv,y-mu)
W = np.diag(mu)
X_tWX = np.matmul(np.matmul(X.transpose(),W),X)
X_tWX_inv = np.linalg.inv(X_tWX)
X_tWz = np.matmul(np.matmul(X.transpose(),W),z)
next_beta = np.matmul(X_tWX_inv,X_tWz)
diff = np.linalg.norm(next_beta-beta)
beta = next_beta
if diff < epsilon:
break
beta와 Deviance와 Pearson 통계량을 계산하고 확인해본다. 이때 로그함수 안에 0 값이 있어서 경고가 발생하는데 이 값은 Deviance 계산 시 무시되므로 신경 쓰지 않아도 된다.
## calculate deviance and Pearson statistics
mu = np.exp(X.dot(beta))
deviance = 2*np.sum(y*np.log(y/mu))
pearson_statistics = np.sum(np.square(y-mu)/mu)
print('Parameter : ',beta)
print('deviance : ',deviance)
print('Pearson Statistics : ', pearson_statistics)
이번엔 statsmodels 라이브러리를 이용해보자. GLM을 이용하여 모형 적합이 가능하고 이때 Poisson GLM을 적용할 것이므로 family인자에 Poisson()을 넣어준다.
y_column = 'fupacts'
x_columns = list(df.columns)
x_columns.remove(y_column)
y = df[y_column]
X = df[x_columns]
model = GLM(y,X,family=Poisson()).fit()
results = model.summary()
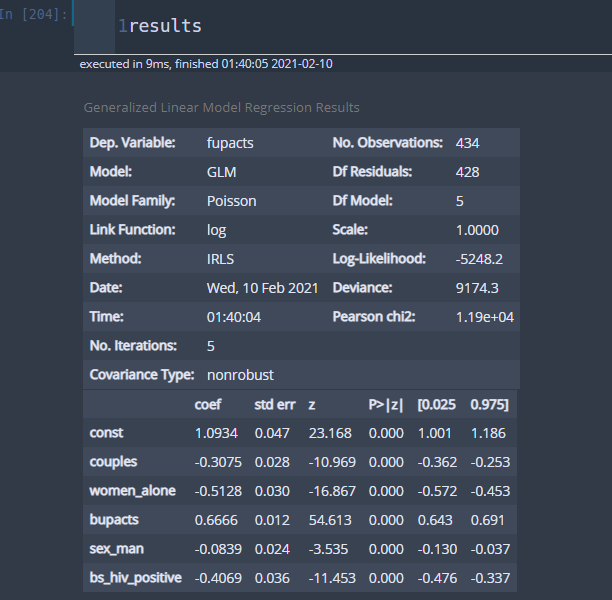
앞서 본 결과와 동일하다. 앞으로는 statsmodels를 사용하자.
이제 모형 적합이 잘되었는지 시각적으로 확인해보자. 먼저 Standardized Deviance 잔차를 구한다. Standardized Deviance는 statsmodels에서 제공하지 않는 것으로 판단된다. 따라서 직접 구해야한다.
phi = 1
W_sqrt = np.diag(np.sqrt(mu))
W_sqrtX = W_sqrt.dot(X)
H_w = W_sqrtX.dot(X_tWX_inv.dot(W_sqrtX.T))
h = np.array([H_w[i][i] for i in range(len(mu))])
dev_residual = []
for i, c in enumerate(y):
if c == 0:
dev_residual.append(0)
else:
dev_r = np.sqrt(2*(c*np.log(c/mu[i])-c+mu[i]))*np.sign(c-mu[i])
dev_residual.append(dev_r)
dev_residual = np.array(dev_residual)
standardized_dev_residual = dev_residual/np.sqrt(phi*(1-h))
vst_mu = 2*np.sqrt(mu) ## variance stabilizing transformation of fitted values
잔차도를 그려보자. 트렌드를 확인하기 위하여 lowess 함수를 사용하였다.
## residual plot
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
vm_order = np.argsort(vst_mu)
ys = lowess(standardized_dev_residual[vm_order],vst_mu[vm_order])[:,1]
plt.scatter(vst_mu,standardized_dev_residual)
plt.plot(vst_mu[vm_order],ys,color='red')
plt.show()
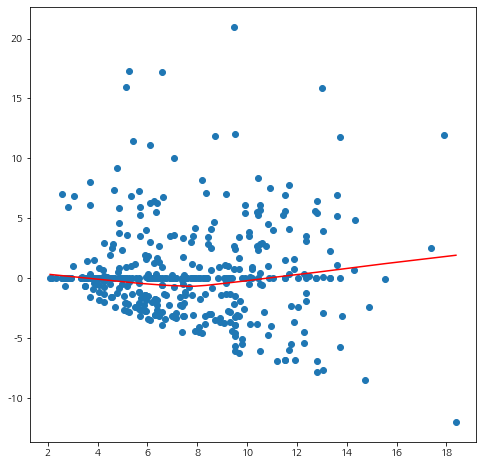
흠 뭔가 애매하긴 하다. 트렌드 곡선을 보았을 때는 특별한 패턴은 없는 것 같다. 이번엔 분산 함수의 적절성을 확인해보자. 잔차의 절대값을 이용한다.
abs_res = np.abs(standardized_dev_residual)
mu_order = np.argsort(mu)
ys = lowess(abs_res[mu_order],mu[mu_order])[:,1]
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(mu,abs_res)
plt.plot(mu[mu_order],ys,color='red')
plt.show()
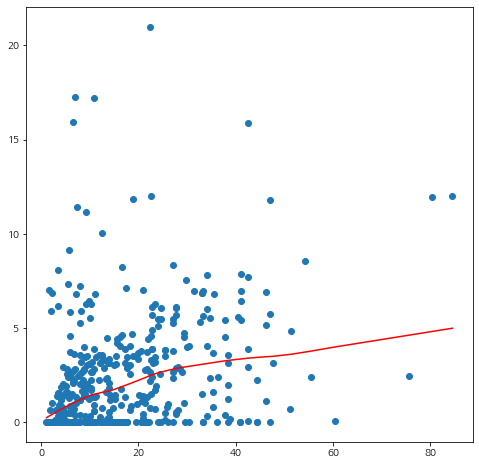
잔차의 변동성이 적합값에 따라 조금씩 증가하는 것 같다. 이번엔 연결 함수의 적절성을 확인해보자.
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
eta_order = np.argsort(eta)
ys = lowess(z[eta_order],eta[eta_order])[:,1]
plt.scatter(eta,z)
plt.plot(eta[eta_order],ys,color='red')
plt.show()
중간중간 튀는 값은 있지만 일반적인 트렌드는 직선 패턴으로 나타난다. 역시 Poisson GLM의 연결함수는 로그함수가 국룰이다.
이번엔 모형 비교를 해볼 것이다. Deviance를 이용하여 후진 소거법을 수행했다. 즉, 전체 변수를 다 사용한 모형에서 필요 없는 변수를 모형 비교를 통하여 제거해 나갈 것이다.
## 후진 소거법
y_column = 'fupacts'
x_columns = list(df.columns)
x_columns.remove(y_column)
x_columns.remove('const')
y = df[y_column] ## 반응 변수
selected_variables = x_columns ## 초기에는 모든 변수가 선택된 상태
sl_remove = 0.05 ## 유의수준
while len(selected_variables) > 0:
X = sm.add_constant(df[selected_variables])
dev1 = GLM(y,X,family=Poisson()).fit().deviance
min_dev_diff = np.infty
for sv in selected_variables:
temp_svs = selected_variables.copy()
temp_svs.remove(sv)
temp_X = sm.add_constant(df[temp_svs])
dev2 = GLM(y,temp_X,family=Poisson()).fit().deviance
dev_diff = dev2-dev1
if dev_diff < min_dev_diff:
min_dev_diff = dev_diff
target_variable = sv
p_val = 1-chi2.cdf(min_dev_diff,df=1)
if p_val < sl_remove:
break
else:
selected_variables.remove(sv)
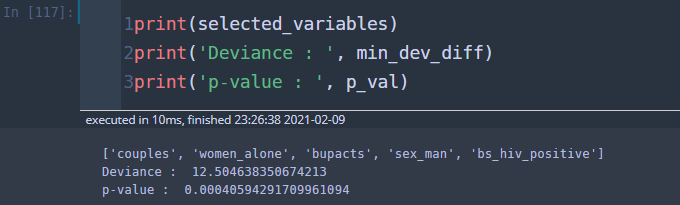
후진 소거법 결과 변수 제거는 일어나지 않았고 전체 변수를 이용한 모형이 가장 좋은 것으로 확인되었다.
참고자료
McCullagh, Nelder - Generalized Linear Models
Alan Agresti - Foundations of Linear and Generalized Linear Models
Youngjo Lee 외 두 명 - Generalized Linear Models with Random Effects Unified Analysis via H-likelihood
댓글