이번 포스팅에서는 Grouped Binary(GB) 데이터가 주어졌을 때 GLM 모형을 적합하는 방법에 대하여 알아보려고 한다. GLM 모형 적합에 대한 내용은 여기를 참고하기 바란다. 여기서 다루는 내용은 다음과 같다.
1. Grouped Binary 데이터란?
Grouped Binary 데이터가 생소할 수도 있으니 이것이 무엇인지 확인해보자. Binary라는 것은 관심의 대상이 되는 변수가 2개의 클래스를 갖는 범주형 데이터를 의미한다. Grouped Binary 데이터는 각 그룹별로 Binary 데이터의 개수와 관심 범주의 비율로 이루어진 데이터를 의미한다. 물론 각 그룹별 설명변수도 있을 수 있다.
예를 들어보자. 어느 고등학교의 2학년은 10반까지 있고 관심의 대상이 되는 범주가 남자라고 하자. 또한 각 반별로 작년 2학기 기말고사 수학 평균 점수가 있다고 하자. 그렇다면 관심의 대상이 되는 범주가 남자 또는 여자이며 범주가 2개이다. 그리고 각 반별로 학생 수와 남자 학생의 비율이 있으므로 Grouped Binary 데이터가 된다. 또한 수학 평균 점수는 반별 설명변수가 된다. 이를 테이블로 나타내면 아래와 같을 것이다.

2. 모형 적합 알고리즘 유도
먼저 $i$ 번째 그룹에 대하여 관심의 대상이 되는 범주의 비율을 $y_i \;(i=1, \ldots, n)$, 각 그룹의 데이터 개수를 $n_i$라 하자. 그리고 $i$ 번째 설명 변수 벡터를 $\tilde{x}_i=(1, x_{1i}, x_{2i}, \ldots, x_{pi})^t$라 하자.
여기서는 Fisher Scoring 알고리즘을 유도할 것이다.
1. 모형 설정
관심의 대상이 되는 범주가 나타난 것을 성공이라는 사건으로 취급할 경우 $n_iy_i$는 총 $n_i$번의 시도 중에서 성공 횟수로 볼 수 있다. 따라서 성공확률을 $p_i$라 했을 때, $n_iy_i$는 이항분포 $B(n_i, p_i)$를 따른다고 할 수 있다. 여기서 데이터를 통해서 추정해야 할 부분은 $p_i$이고 연결 함수 $g$를 이용하여 다음과 같이 모형을 설정한다.
$$g(p_i) = \beta^t\tilde{x}_i\tag{1}$$
2. 우도 함수(Likelihood Function)
$$\begin{align}f(y_i | p_i, n_i) &= \frac{n_i}{(n_iy_i)!(n_i-n_iy_i)!}p_i^{n_iy_i}(1-p_i)^{n_i-n_iy_i}\\ \\&= \exp\left[n_iy_i\log p_i + (n_i-n_iy_i)\log (1-p_i) + \log \frac{n_i}{(n_iy_i)!(n_i-n_iy_i)!}\right] \\ \\&= \exp\left\{ n_i\left [ y_i\log\left(\frac{p_i}{1-p_i} \right) + \log(1-p_i) \right ] + \log \frac{n_i}{(n_iy_i)!(n_i-n_iy_i)!} \right\} \\ \\ &= \exp \{[y_i\theta_i-b(\theta_i)]/a(\phi)+c(y_i,\phi)\}\end{align}$$
여기서 $\theta_i = \log[p_i/(1-p_i)]$, $b(\theta_i) = \log[1+\exp(\theta_i)]$, $a(\phi)=1/n_i$, $c(y_i, \phi)=\log [n_i/(n_iy_i)!(n_i-n_iy_i)!]$이다. 따라서 $y_i$의 확률분포는 exponential dispersion family가 된다.
3. 연결 함수(Link Function)
이제 연결 함수 $g$를 정해야 한다. $y_i$의 확률분포가 exponential dispersion family이므로 canonical 연결 함수를 쓰면 된다. canonical 연결 함수의 정의는 여기를 참고하자.
$$\theta_i = \eta_i = g(\mu_i) = g(p_i) = \log\left(\frac{p_i}{1-p_i}\right)$$
여기서 $\mu_i=E(y_i)=p_i$이다.
4. 알고리즘
모형 행렬(Model Matrix)을 $X=(x_{ij})$라 하자. 알고리즘을 유도하기 위하여 $D$는 $i$번째 대각 원소가 $d_i=\partial \mu_i/\partial \eta_i$인 대각행렬, $W$는 $i$번째 대각원소가 $w_i=\frac{(\partial \mu_i/\partial\eta_i)^2}{\text{var}(y_i)}$인 대각 행렬을 계산해야 한다.
$\mu_i = p_i$, $\eta_i = \log[p_i/(1-p_i)]$임을 이용하면 $d_i$를 다음과 같이 계산할 수 있다.
$$d_i = \frac{\partial p_i}{\partial \eta_i} = \left(\frac{\partial \eta_i}{\partial p_i}\right)^{-1} = p_i(1-p_i)$$
$\text{var}(y_i)=p_i(1-p_i)$임을 이용하면 $w_i$를 다음과 같이 계산할 수 있다.
$$w_i=\frac{(\partial p_i/\partial\eta_i)^2}{\text{var}(y_i)}=\frac{[p_i(1-p_i)]^2}{p_i(1-p_i)}=p_i(1-p_i)$$
이제 Fisher Scoring 알고리즘을 유도할 수 있다(연결 함수가 canonical인 경우 이는 Newton-Raphson 알고리즘과 동일하다).
$\beta^{(k)}$가 주어졌을 때 $p_i$의 추정값 $p_i^{(k)}$는 (1)과 연결 함수 $g$를 이용하여 다음과 같이 계산할 수 있다.
$$p_i^{(k)} = \frac{\exp(\beta^{(k)t}\tilde{x}_i)}{1+\exp(\beta^{(k)t}\tilde{x}_i)}\tag{2}$$
이제 식 (2)를 이용하여 $W$ 와 $D$에서 $p_i$를 $p_i^{(k)}$로 대체한 행렬을 각각 $W^{(k)}$ 와 $D^{(k)}$라고 하자. 이제 다음과 같이 새로운 반응 변수 $z^{(k)}$를 정의한다.
$$z^{(k)}=X\beta^{(k)}+(D^{(k)})^{-1}(\textbf{y}-\pmb{\mu})$$
이로부터 $\beta^{(k+1)}$을 다음과 같이 구할 수 있다.
$$\beta^{(k+1)} = (X^tW^{(k)}X)^{-1}X^tW^{(k)}z^{(k)}$$
3. 실제 데이터 적용
이제 실제 데이터를 이용하여 GLM을 적합해보자. 데이터를 다운받아주자.
필요한 모듈을 임포트하고 데이터를 불러오자.
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
from scipy.stats import norm
df = pd.read_csv('./coupon_effectiveness.csv')
데이터를 간단하게 설명하자면 5가지의 할인율(Price_Reduction)이 적용되는 쿠폰을 각 할인율별로 200가구(Num_of_Households)에 뿌렸다고 한다. 이때 쿠폰을 사용한 가구의 비율(Prop_of_CR)과 할인율과의 관계를 알아보는 것이 이 데이터 분석의 목적이라고 한다.

모형을 적합해보자. 먼저 필요한 함수를 정의한다. 여기서는 로짓 함수와 시그모이드 함수를 정의했다.
## 필요 함수
def get_pi(x,b):
return np.exp(np.inner(x,b))/(1+np.exp(np.inner(x,b)))
def logit(x):
return np.log(x/(1-x))
반응 변수와 모형 행렬을 정의한다. statsmodels.api가 제공하는 add_constant를 이용하여 절편항을 추가한다.
## 세팅
y = df['Prop_of_CR']
X = df['Price_Reduction'] ## 모델 매트릭스
X = sm.add_constant(X)
X = np.array(X)
X_t = X.transpose()
추정량의 초기값을 정해준다. 초기값을 정하는 방법은 여기에 정리해놓았으니 살펴보기 바란다.
# 베타 초기값
X_tX_inv = np.linalg.inv(np.matmul(X_t,X))
beta = np.matmul(X_tX_inv,np.matmul(X_t,logit(y)))
다음은 모형 적합 과정을 구현한 것이다.
## 모델 적합
max_iter = 100
tolerance = 0.0001
num_iter = 0
betas = [] ## 스텝별로 베타 값을 저장
betas.append(beta) ## 초기값 저장
while num_iter <= max_iter:
num_iter += 1
W_element = [] ## W의 대각원소
D_element = [] ## D의 대각 원소
pis = []
for i in range(len(df)):
pi = get_pi(X[i],beta)
W_element.append(pi*(1-pi))
D_element.append(pi*(1-pi))
pis.append(pi)
pis = np.array(pis)
W = np.diag(W_element) ## W
D = np.diag(D_element) ## D
X_tWX = np.matmul(np.matmul(X_t,W),X)
X_tWX_inv = np.linalg.inv(X_tWX)
mu = pis ## mu
z = np.matmul(X,beta)+np.matmul(np.linalg.inv(D),y-mu) ## z
X_tWz = np.matmul(X_t,np.matmul(W,z))
next_beta = np.matmul(X_tWX_inv,X_tWz) ## next beta
diff = np.linalg.norm(next_beta-beta)
if diff < tolerance:
beta = next_beta
betas.append(beta)
print('tolerance acheived')
break
else:
beta = next_beta
betas.append(beta)
line 2~3
최대 반복 횟수와 오차 범위를 설정하여 반복을 언제 멈출 것인지 정한다.
line 7~37
$W^{(k)}$(line 19), $D^{(k)}$(line 20), $\pmb{\mu}$(line 23)를 구하고 $z^{(k)}$를 계산한다(line 24). 마지막으로 $\beta^{(k+1)}$을 계산한다(line 27).
최종 추정량과 스텝을 출력해본다.
총스텝은 3번이며 최종 추정량에서 절편은 -2.0443, 기울기는 0.0968로 나왔다. 이번엔 초기값을 모두 0으로 두고 모형 적합을 해보자. 코드 부분에서 초기값만 아래와 같이 바꿔준다.
# 베타 초기값
beta = np.array([0,0]) ## 초기값
결과를 출력해보자.

추정량은 정확하지만 스텝 한 번이 더 늘어났다. 첫 번째 초기값이 더 좋긴 하지만 초기값을 0으로 놓고 해도 동일한 결과를 얻는다. 다음은 초기값에 따른 기울기 추정량의 변화를 시각화해보았다.

수직 점선은 마지막 스텝을 나타낸다. 다음은 추정량의 95% 신뢰 구간을 구해보려고 한다. 이는 다음과 같이 추정량의 점근 분포가 정규 분포를 따른다는 사실에 기반한 것이다.
$$\hat{\beta} \sim N(\beta, (X^tWX)^{-1})$$
## 신뢰구간
alpha = 0.05
for i in range(X_tWX_inv.shape[0]):
upper_limit = beta[i] + norm.ppf(1-alpha/2)*np.sqrt(X_tWX_inv[i][i])
lower_limit = beta[i] - norm.ppf(1-alpha/2)*np.sqrt(X_tWX_inv[i][i])
print(lower_limit, upper_limit)

첫 번째 줄은 절편의 신뢰구간이고, 두 번째 줄은 기울기의 신뢰구간이다. 두 개 모두 0을 포함하므로 통계적으로 유의하지 않다고 할 수 있다.
이번엔 statsmodels에서 제공하는 Logit을 이용하여 모형을 적합해보자.
## statsmodels 이용하기
y = df['Prop_of_CR']
X = df['Price_Reduction']
X = sm.add_constant(X)
fit = sm.Logit(y,X).fit()
모형 적합 결과는 summary를 이용하여 볼 수 있다.
fit.summary()
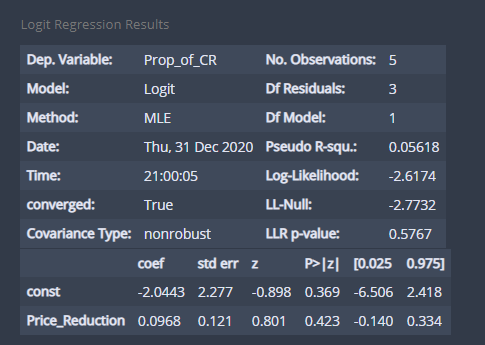
추정량과 신뢰구간 모두 동일하다. 구현을 해보고 결과가 동일하다는 것을 알았으니 이젠 statsmodel에서 제공하는 Logit 함수를 사용하자.
참고자료
Kutner 외 2명 - Applied Linear Regression Models
Alen Agresti - Foundations of Linear and Generalized Linear Models






댓글