안녕하세요~ 꽁냥이에요!
데이터 분석시 이상치는 관심을 갖고 살펴보아야하는데요. 이상치는 데이터를 만드는 사람의 실수에 의해서 발생할 수도 있고 데이터를 생성하는 시스템에 의하여 발생할 수도 있습니다. 이상치는 회귀 분석에서 양날의 검이라고도 할 수 있는데요. 이상치로 인하여 모형의 해석(회귀 계수의 해석)이 정확하지 않게 될 수 있지만 중요한 정보(시스템의 고장, 새로운 연관성의 발견 등)를 제공하기 때문이지요.
또한 이상치 중에서도 모형 여기서는 회귀계수 값의 변화를 크게 만드는 것이 있고 아닌 것이 있습니다. 이때 이상치 중에서 회귀계수 값의 변화를 크게 만드는 데이터를 영향점(Influential data)이라고 합니다. 영향점이라고 판단되는 데이터는 모형을 크게 변화시키기 때문에 제외시키기도 하지만 상황에 따라서 포함시키기도 합니다.
이번 포스팅에서는 이상치와 영향점을 확인하는 방법에 대해서 알아보려고 합니다.
이상치(Outlier) 확인
이상치는 반응변수에 대한 이상치와 설명변수에 대한 이상치가 있습니다. 여기서 반응변수를 $y = (y_1, y_2, \cdots, y_n)^t$라 하고 설명변수로 이루어진 $n\times p$ 행렬을 $X$라 하겠습니다. 즉, $x_i = (x_{i1}, \cdots , x_{ip})^t, \;\; i=1,\cdots,n$ 이라 한다면 $X$의 $i$번째 행은 $x_i$가 되는 것입니다. 이제 다음과 같은 모형을 생각해보겠습니다.
$$ E(y) = X\beta$$
여기서 $\beta=(\beta_1, \cdots, \beta_p)^t$ 입니다.
이제 앞서 말한 두가지 이상치에 대해서 살펴보겠습니다.
1. 반응변수에 대한 이상치
반응변수가 연속형인 경우 설명변수가 주어졌을 때 반응변수의 예측분포에서 멀리 떨어져있는 값을 반응변수에 대한 이상치라고 합니다.
2. 설명변수에 대한 이상치
설명변수에 대한 이상치는 설명변수 값들의 분포로 부터 멀리 떨어져 있는 값을 말합니다.
이상치는 반응변수에 대한 이상치, 설명변수에 대한 이상치 둘 중 하나일 수도 있고 둘다 될 수도 있습니다. 예를 들어보겠습니다.

위 그림은 $x$와 $y$의 분포를 나타낸 것입니다. 여기서 1번과 3번은 반응변수($y$)에 대한 이상치입니다. 왜냐하면 데이터에서 설명변수($x$)가 주어졌을 때 1, 3번에 대한 예측분포는 아래와 같이 4번, 5번 주변(초록색 범위 안쪽)에 있어야 하지만 실제 관측된 1, 3번 데이터는 예상보다 멀리 떨어져있기 때문입니다.

그리고 2, 3번 데이터는 설명변수에 대한 이상치인 것을 쉽게 알 수 있습니다. 설명변수의 중심으로부터 멀리 떨어져 있기 때문이지요. 특히 3번 데이터는 반응변수, 설명변수에 대한 이상치인 것에 주목하시기 바랍니다.
3. 반응변수에 대한 이상치 확인
위 그림으로부터 반응변수에 대한 이상치를 확인하는 방법을 유추할 수 있습니다. 바로 실제 반응변수 관측값과 해당 반응변수를 빼고 만들어진 회귀모형을 이용한 추정값의 차이를 이용하면 됩니다.
$$d_i = y_i-\hat{y}_{i(i)}$$
여기서 $\hat{y}_{i(i)}$는 $i$번째 데이터를 제외하여 구한 회귀모형으로 추정한 $i$번째 반응변수의 추정값입니다. 즉, $i$번째 데이터를 제외하고 계산한 회귀계수를 $\beta_{(i)}$라 하면 $\hat{y}_{i(i)}=x_i^t\hat{\beta}_{(i)}$ 입니다. 그리고 다음과 같이 Studentized Deleted Residual(이하 SDR) $t_i$를 정의합니다.
$$t_i = \frac{d_i}{s(d_i)}\tag{2}$$
여기서 $s(d_i)$는 $d_i$의 표준편차입니다. 식 (2)는 다음과 같이 변형이 가능합니다.
$$t_i = e_i\left [ \frac{n-p-1}{SSE(1-h_{ii})-e_i^2}\right ]^{1/2}$$
이때 $SSE$는 모든 데이터를 이용하여 구한 회귀모형이 있을 때, 잔차제곱합이고 $e_i$는 $i$번째 잔차, $h_{ii}$는 Hat Matrix $H=X(X^tX)^{-1}X^t$의 $i$번째 대각원소입니다(Hat Matrix 덕분에 $n$번 회귀모형을 적합하지 않고 한번에 SDR을 구할 수 있습니다 ^^).
만약 회귀모형이 참인경우 $t_i$는 자유도가 $n-p-1$인 $t$분포를 따른다고 알려져 있습니다. 따라서 반응변수에 대한 이상치를 결정하기 위한 기준 값은 유의수준 $\alpha$일 때 자유도가 $n-p-1$인 $t$분포의 오른쪽 꼬리값인 $t(1-\alpha/2n;n-p-1)$로 정할 수 있습니다. 즉, $|t_i| > t(1-\alpha/2n;n-p-1)$인 경우 반응변수에 대한 이상치라고 간주할 수 있지요.
이제 실제 데이터를 가지고 이상치를 확인해보겠습니다. 아래 첨부파일을 다운받아주세요.
필요한 모듈을 임포트하고 데이터를 불러와주세요.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['axes.unicode_minus'] = False ## 마이나스 '-' 표시 제대로 출력
from scipy.stats import t
from statsmodels.formula.api import ols
df = pd.read_csv('body_fat_data_reduced.csv')

다음은 코드는 SDR를 계산하고 시각화하는 코드입니다.
## 반응변수에 대한 이상치 확인
def hat_matrix(X): ## Hat Matrix를 계산하는 함수
X = np.array(X)
XtX = np.matmul(X.transpose(),X)
XtX_inv = np.linalg.inv(XtX)
return np.matmul(np.matmul(X, XtX_inv),X.transpose())
fit = ols('Body_fat ~ Tricep_ST + Thigh_C',data=df).fit() ## 선형 모형 적합
X = df[['Tricep_ST','Thigh_C']]
X.insert(0,'Intercept',[1]*len(df)) ## 절편항 추가
n = len(df) ## 데이터 개수
p = len(X.columns) ## 절편항을 포함한 회귀 계수의 개수
hat_mat = hat_matrix(X) ## Hat Matrix
h = np.array([hat_mat[i][i] for i in range(n)]) ##레버리지
e = fit.resid ## 잔차
SSE = np.sum(np.square(e)) ## 잔차제곱합
sdr = e*np.sqrt((n-p-1)/(SSE*(1-h)-np.square(e))) ## Studentized Deleted Residual
alpha = 0.1 ## 유의수준
critical_value = t.ppf(1-alpha/(2*n), n-p-1) ## 기준값
## 시각화
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
idx = range(1,n+1)
plt.scatter(idx, sdr)
plt.axhline(critical_value,linestyle='--',color='red')
plt.axhline(-critical_value,linestyle='--',color='red')
plt.xticks(idx)
plt.show()
위 코드를 실행해보세요~
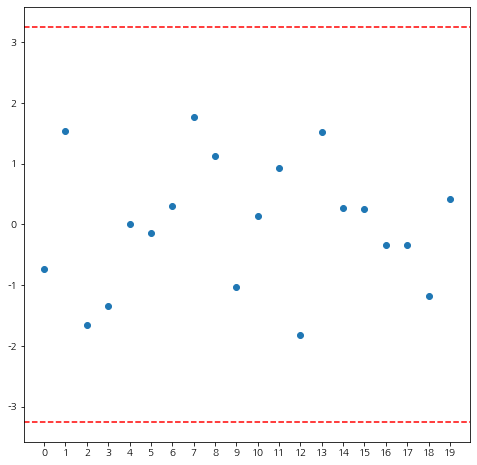
모든 SDR이 기준값(붉은 선)안에 있으므로 반응변수에 대한 이상치는 없다고 판단할 수 있습니다.
4. 설명변수에 대한 이상치 확인
설명변수에 대한 이상치를 확인하는 방법으로 위에서 정의한 Hat Matrix의 대각 원소(Leverage)를 이용합니다. 이에 대한 이유를 살펴보기 위하여 다음과 같이 마할라노비스 거리(Mahalanobis Distance) $MD_i$를 생각해봅시다.
$$MD_i = (x_i-\bar{x})^tC^{-1}(x_i-\bar{x})$$
여기서 $\bar{x}$는 설명변수(절편항 제외)의 평균벡터 즉, $\bar{x}=(\bar{x}_1,\cdots,\bar{x}_p)^t, \bar{x}_j=\sum_{i=1}^nx_{ij}/n$ 이고 $C$는 설명변수의 표본공분산행렬 즉, $C_{jk}=\sum_{i=1}^n(x_{ij}-\bar{x}_j)(x_{ik}-\bar{x}_k)/(n-1)$ 입니다. 이때 Hat Matrix의 대각원소를 $h_{ii}$라고 할때 $h_{ii}$와 $MD_i$사이에는 다음과 같은 관계가 성립합니다.
$$MD_i^2=(n-1)\left(h_{ii}-\frac{1}{n}\right)$$
위 식을 보면 $h_{ii}$가 커질 수록 $MD_i$의 값이 크다는 것을 알 수 있습니다. 마할라노비스 거리 $MD_i$는 설명변수 벡터가 평균으로 부터 얼마나 떨어져있는지를 재는 거리함수이므로 $h_{ii}$가 클수록 해당 설명변수 벡터가 평균으로 부터 멀리 떨어져 있다는 것을 알수 있지요.
경험적으로 $h_{ii}$ 값이 평균 Leverage $\bar{h}=\sum_{i=1}^nh_{ii}/n=p/n$보다 2배이상 크다면 해당 설명변수 벡터 $x_i$를 이상치라고 판단합니다.
아래 코드는 Hat Matrix의 대각 원소를 계산하고 시각화하는 코드입니다.
## 설명변수에 대한 이상치 확인
def hat_matrix(X): ## Hat Matrix를 계산하는 함수
X = np.array(X)
XtX = np.matmul(X.transpose(),X)
XtX_inv = np.linalg.inv(XtX)
return np.matmul(np.matmul(X, XtX_inv),X.transpose())
X = df[['Tricep_ST','Thigh_C']]
X.insert(0,'Intercept',[1]*len(df)) ## 절편항 추가
n = len(df) ## 데이터 개수
p = len(X.columns) ## 절편항을 포함한 회귀 계수의 개수
hat_mat = hat_matrix(X) ## Hat Matrix
h = np.array([hat_mat[i][i] for i in range(n)]) ##레버리지
mean_h = p/n ##평균 레버리지
outlier_idx = np.where(h>2*mean_h)[0]
outlier = [h[i] for i in outlier_idx]
## 시각화
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
idx = range(1,n+1)
plt.scatter(idx, h)
plt.scatter(outlier_idx+1,outlier,s=200,facecolor='none',edgecolor='red')
for i in range(len(outlier)):
ax.annotate(str(outlier_idx[i]+1),(outlier_idx[i]+1.5,outlier[i]),fontsize=13)
plt.axhline(2*mean_h,linestyle='--',color='red')
plt.xticks(idx)
plt.show()
위 코드를 실행해보세요.

보시는 바와 같이 3, 15번 데이터가 설명변수에 대한 이상치인 것을 확인할 수 있습니다. 실제로 아래의 설명변수의 분포를 보면 3, 15번 데이터가 평균으로부터 멀리 떨어져 있다는 것을 확인할 수 있습니다.

위 시각화 코드는 아래와 같습니다.
## 설명변수 분포
mean_x = np.mean(df['Tricep_ST'])
mean_y = np.mean(df['Thigh_C'])
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
fontsize = 13
plt.xlabel('Tricep_ST',fontsize=fontsize)
plt.ylabel('Thigh_C',fontsize=fontsize)
plt.scatter(df['Tricep_ST'], df['Thigh_C'])
plt.scatter(mean_x,mean_y,alpha=0.3,color='green',s=200, label='Mean')
outlier_x = [df['Tricep_ST'][i] for i in outlier_idx]
outlier_y = [df['Thigh_C'][i] for i in outlier_idx]
plt.scatter(outlier_x, outlier_y, s=200, facecolor='none', color='red', label='Outlier')
for i in range(len(outlier)):
ax.annotate(str(outlier_idx[i]+1),(outlier_x[i]+0.5,outlier_y[i]),fontsize=13)
plt.legend()
plt.show()영향점(Influential Data) 확인
특정 데이터가 이상치라고 판단이 됐다면 이를 제외할지 말지를 결정해야할 것입니다. 만약 이상치가 실수에 의해서 만들어졌으면 당연히 제외해야하고 아니라면 이상치가 회귀모형을 확연히 달라지게 하는지를 살펴보아야합니다. 즉, 모든 데이터를 이용한 회귀모형과 이상치를 제외한 회귀모형의 차이가 큰지를 살펴보아야한다는 것이지요. 이 때 회귀모형의 차이를 크게 만드는 데이터를 영향점(Influential Data)이라고 합니다.
영향점을 확인하기 위한 측도(Measure)에는 DFFITS, Cook's Distance, DFBETAS가 있습니다.
1. DFFITS
DFFITS(DFference in FITS)는 특정 데이터를 제외한 회귀 모형 적합값과 모든 데이터를 이용한 회귀 모형 적합값의 차이를 이용하며 다음과 같이 정의합니다.
$$(DFFITS)_i = \frac{\hat{Y}_i-\hat{Y}_{i(i)}}{\sqrt{MSE_{(i)}h_{ii}}}\tag{1}$$
여기서 $MSE_{(i)}$는 $i$번째 데이터를 제외한 회귀모형의 평균잔차제곱합입니다. (1)식은 아래와 같이 변형할 수 있습니다.
$$(DFFITS)_i=t_i\left(\frac{h_{ii}}{1-h_{ii}}\right)^{1/2}$$
DFFITS를 이용한 영향점을 판단하는 기준은 경험적으로 데이터 개수가 적은 경우 DIFFIT의 절대값이 1보다 큰 경우 데이터 개수가 많은 경우에는 $2\sqrt{p/n}$보다 큰 경우 영향점이라고 판단합니다.
영향점을 판단하는 기준은 위에서 소개한 것 이외에도 여러가지가 있으며 확실한 판단 근거가아닌 일종에 가이드라인으로 참고하시길 바랍니다.
2. Cook's Distance
Cook's Distance 또한 DFFITS와 같이 특정 데이터를 제외한 회귀 모형 적합값과 모든 데이터를 이용한 회귀 모형 적합값의 차이를 이용합니다. 차이점은 DFFIT은 개별 데이터에 대한 차이를 이용하지만 Cook's Distance는 개별 데이터 차이의 제곱을 합산한다는 것입니다. Cook's Distance $D_i$는 아래와 같이 정의합니다.
$$D_i=\frac{\sum_{j=1}^{n}(\hat{Y}_j-\hat{Y}_{j(i)})^2}{pMSE}\tag{2}$$
(2)식은 다음과 같이 변형가능합니다.
$$D_i=\frac{e_i^2}{pMSE}\left[\frac{h_{ii}}{(1-h_{ii})^2}\right]$$
영향점을 판단하는 기준으로는 분자의 자유도가 $p$, 분모의 자유도가 $n-p-1$인 $F$분포를 고려하며 $D_i$에 해당하는 누적 확률값이 0.2보다 작다면 영향점이 아니라고 판 단하며 0.5이상인 경우에는 영향점이라고 판단합니다. 또한 데이터가 많을 경우 $D_i$가 1보다 큰경우 영향점이라고 판단합니다.
3. DFBETAS
DFBETAS(DFference in BETAS)는 특정 데이터를 제외한 회귀 계수와 모든 데이터를 이용한 회귀 계수의 차이를 이용하며 다음과 같이 정의합니다.
$$(DFBETAS)_{k(i)}=\frac{\hat{\beta}_k-\hat{\beta}_{k(i)}}{\sqrt{MSE_{(i)}c_{kk}}}, \:\:k=1, 2, \cdots, p\tag{3}$$
여기서 $c_{kk}$는 $(X^tX)^{-1}$의 $k$번째 대각원소입니다. (3)식은 다음과 같이 변형가능합니다.
$$(DFBETAS)_{k(i)}=\frac{a_{ki}e_i}{1-h_{ii}}\left[\frac{1}{n-p-1}\left(SSE-\frac{e_i^2}{1-h_{ii}}\right)\right]$$
여기서 $a_{ki}$는 $(X^tX)^{-1}x_i=(a_{1i},\cdots,a_{pi})^t$의 $k$번째 원소입니다.
영향점을 판단하는 기준은 데이터의 개수가 적은 경우에는 $(DFBETAS)_{k(i)}$의 절대값이 1보다 큰 경우, 데이터가 많은 경우에는 $(DFBETAS)_{k(i)}$의 절대값이 $2/\sqrt{n}$보다 큰 경우 영향점이라고 판단합니다.
이제 DFFITS, Cook's Distance, DFBETAS를 실제 데이터를 통해서 확인해보겠습니다. 먼저 필요한 모듈을 임포트하고 데이터를 불러오겠습니다.
import pandas as pd
import numpy as np
from statsmodels.formula.api import ols
df = pd.read_csv('./body_fat_data_reduced.csv')
df.insert(0,'Intercept',[1]*len(df)) ##절편항 추가
fit = ols('Body_fat ~ Tricep_ST + Thigh_C',data=df).fit() ## 선형 모형 적합
X = df[['Intercept','Tricep_ST','Thigh_C']] ## Design Matrix
def hat_matrix(X):
## Hat Matrix를 계산하는 함수
X = np.array(X)
XtX = np.matmul(X.transpose(),X)
XtX_inv = np.linalg.inv(XtX)
return np.matmul(np.matmul(X, XtX_inv),X.transpose())
X = np.array(X)
XtX = np.matmul(X.transpose(),X)
XtX_inv = np.linalg.inv(XtX)
n = len(df) ## 데이터 개수
p = X.shape[1] ## 파라미터 개수
hat = hat_matrix(X) ## Hat Matrix
diag_hat = np.array([hat[i][i] for i in range(n)]) ##레버리지
e = fit.resid ## 잔차
SSE = np.sum(np.square(fit.resid)) ## 잔차제곱합
MSE = SSE/(n-p) ## 평균잔차제곱합
## DFFITS
DFFITS = e*np.sqrt(((n-p-1)/(SSE*(1-diag_hat)-np.square(e))))*np.sqrt(diag_hat/(1-diag_hat))
## Cook's Distance
D = np.square(e)*(diag_hat/np.square(1-diag_hat))/(p*MSE)
## DFBETAS
DFBETAS = []
diag_c = np.array([XtX_inv[i][i] for i in range(p)])
for i in range(n):
x = np.expand_dims(X[i], axis=1)
diff_beta = np.matmul(XtX_inv,x)*e[i]/(1-diag_hat[i])
diff_beta = diff_beta.squeeze(axis=1)
deleted_MSE = (SSE-np.square(e[i])/(1-diag_hat[i]))/(n-p-1)
std_db = np.sqrt(deleted_MSE*diag_c)
DFBETAS.append(diff_beta/std_db)
DFBETAS = np.array(DFBETAS)
df_res = pd.DataFrame()
df_res['DFFITS'] = DFFITS
df_res['D'] = D
df_numerator = p
df_denominator = n-p-1
critical_value = f.cdf(D,df_numerator,df_denominator) ## Cook's Distance 기준값
temp_df = pd.DataFrame(DFBETAS, columns = ['DFBETAS_'+x for x in df.columns[:-1]])
df_res = pd.concat([df_res,temp_df],axis=1)
df_res.insert(2,'CV',critical_value)
위 코드를 실행하여 df_res에 포함된 결과를 확인해보겠습니다.

먼저 DFFITS와 DFBETAS를 확인해보겠습니다. 데이터가 많지 않으므로 절대값이 1보다 큰 경우를 노란색 박스로 표시하였습니다. 3번째 데이터가 영향점이라고 판단할 수 있습니다. 다음으로 Cook's Distance를 확인해보겠습니다. 해당 $D_i$에 대한 $F$분포의 누적확률을 'CV'열에 나타내었습니다. 3번째 데이터가 가장 큰 값인 0.306입니다. 이는 0.2보다는 크지만 0.5보다는 작으므로 해당 데이터는 회귀모형에 중간정도 영향력을 갖는 데이터라고 할 수 있지요. 종합해보면 3번째 데이터가 영향점이라는 것으로 결론내릴 수 있습니다.
DFFITS, Cook's Distance, DFBETAS는 위와 같이 직접구현할 수도 있지만 fit에 있는 get_influence를 이용하여 구할수 있습니다.
## statsmodel 모듈 이용하기
influence = fit.get_influence()
df_res = pd.DataFrame()
df_res['DFFITS'] = influence.dffits[0] ## DFFITS
df_res['D'] = influence.cooks_distance[0] ## Cook's Distance
## DFBETAS
temp_df = pd.DataFrame(influence.dfbetas, columns = ['DFBETAS_'+x for x in df.columns[:-1]])
df_res = pd.concat([df_res,temp_df],axis=1)
df_res.style.apply(draw_color,axis=0,subset = ['DFFITS','DFBETAS_Tricep_ST','DFBETAS_Thigh_C'])
영향점이라고 판단된다면 이를 제외하거나 제외하지 않는다면 모형을 그대로 유지할지 Robust Regression과 같은 다른 모형을 만들지 정해야합니다.
이상치와 영향점에 대한 분석은 데이터의 오류여부와 해당분야의 전문가와 상의하여 이론적으로 나올 수 있는 값인지 확인하는 등 분석자의 노력과 주관이 필요합니다.
이번 포스팅에서는 이상치와 영향점에 대한 정의와 실제 데이터를 통해서 확인하는 방법에 대해서 알아보았습니다.
지금까지 꽁냥이의 글 읽어주셔서 감사합니다. 다음에도 좋은 내용으로 찾아뵐게요. 안녕히계세요~~!!
이번 포스팅에서 참고한 자료는 다음과 같습니다.
Kutner, Nachtsheim, Neter - Applied Linear Regression Model 4th edition
Influential Observation - Wiki
parker.ad.siu.edu/Olive/ch6.pdf
'데이터 분석 > 데이터 분석' 카테고리의 다른 글
| [회귀 분석] 10. 가중 최소 제곱법(Weigted Least Square)으로 회귀 모형 적합하기 with Python (5) | 2020.12.04 |
|---|---|
| [회귀 분석] 9. 능형 회귀(Ridge regression) 모형 적합하기 with Python (2) | 2020.12.01 |
| [회귀 분석] 7. 다중공선성 확인하기 - 분산 팽창 인자 with Python (10) | 2020.10.05 |
| [회귀 분석] 6. 변수 선택법(Variable Selection) with Python (10) | 2020.10.01 |
| [회귀 분석] 5. 최적 모형 선택(All possible search 또는 Best subsets algorithm) with Python (7) | 2020.09.26 |





댓글