이번 포스팅에서는 각 데이터가 갖고 있는 가중치를 활용한 통계량으로 가중 평균(Weighted Mean), 가중 상관계수( Weighted Correlation ), 가중 분위수(Weighted Quantile)를 소개하고자 한다.
- 목차 -
3. 가중 상관계수( Weighted Correlation )
1. 가중치를 고려하는 이유?
데이터가 주어진 경우 개별 데이터의 가치 또는 신뢰할 수 있는 정도가 다르기 때문에 단순히 주어진 데이터가 아닌 가치나 신뢰도를 반영하기 위해서 고려하는 것이다.
예를 들어 다음과 같이 A 인턴, B 선임, C 팀장에 대해 명목 연봉이 있고 회사의 기여도, 사교성, 리더십 등을 종합적으로 평가한 가치가 주어졌다고 해보자(물론 이러한 가치를 측정하기란 쉽지 않다).
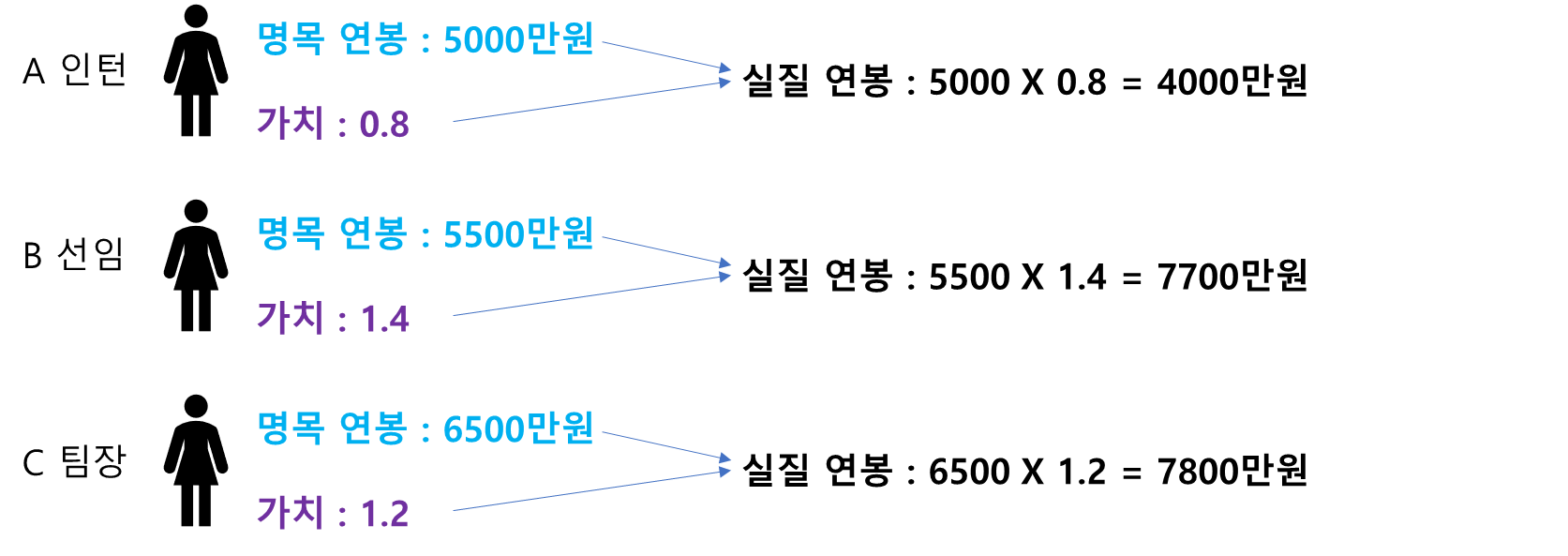
이때 3사람의 평균 연봉을 계산할 때 명목 연봉으로 계산하는 것보다 각 사람들의 가치를 반영한 실질 연봉으로 계산하는 것이 더 합리적일 것이다. 참고로 명목 연봉의 평균은 5667만원, 가치를 반영한 실질 연봉의 평균은 5735만원이며 계산식은 아래와 같다.
$$\frac{5000\cdot 0.8 + 5500\cdot 1.4+6500\cdot1.2}{0.8+1.4+1.2} = 5735$$
가중치가 주어졌다면 이를 이용하여 좀 더 합리적인 통계량을 생각해볼 수 있다. 이제 가중치 기반 통계량에는 어떤 것들이 있는지 살펴보자.
2. 가중 평균(Weighted Mean)
먼저 데이터와 가중치 $x_i, w_i, i=1, \ldots, n$가 있다고 할 때 가중 평균 $\bar{x}_w$을 다음과 같이 정의한다.
$$\bar{x}_w = \frac{\sum_{i=1}^nw_i\cdot x_i}{\sum_{i=1}^nw_i}$$
이제 일반 평균과 가중 평균이 어떻게 차이가 나는지 확인해보자. 아래 코드는 20개의 데이터와 가중치를 생성하고 평균과 가중 평균의 차이를 나타낸 것이다. 이때 각 데이터의 점 크기는 가중치에 비례하여 그리게 하였다.
import numpy as np
import matplotlib.pyplot as plt
def mean(x, weighted=None):
if weighted is None:
return np.mean(x)
return np.sum(x*weighted)/np.sum(weighted)
np.random.seed(100)
size = 20
data = np.random.randint(0, 100, size)
## 평균보다 작은 곳은 작은 가중치 큰 곳은 큰 가중치
weight = np.zeros(size)
lower_idx = np.where(data<=np.mean(data))[0]
weight[lower_idx] = np.random.randint(5, 20, len(lower_idx))
upper_idx = np.where(data>np.mean(data))[0]
weight[upper_idx] = np.random.randint(50, 100, len(upper_idx))
fig = plt.figure(figsize=(10,6))
fig.set_facecolor('white')
plt.scatter(range(len(data)), data, s=weight, label='data')
plt.axhline(np.mean(data), linestyle='--', label='평균', color='k')
plt.axhline(mean(data, weight), linestyle='--', label='가중 평균', color='r')
plt.xticks(range(len(data)), [str(i+1) for i in range(len(data))])
plt.legend()
plt.show()

데이터 값이 높은 쪽에 가중치가 큰 것들이 많으므로 가중 평균은 일반 평균보다 위로 쏠려있다.
3. 가중 상관계수( Weighted Correlation )
가중 상관계수는 다음과 같이 정의된다. 데이터와 가중치 $x_i, y_i, w_i, i=1, \ldots, n$가 있다고 할 때 가중 상관 계수 $\text{corr}(x, y)_w$을 다음과 같이 정의한다.
$$\text{corr}(x, y)_w = \frac{\sum_{i=1}^nw_i(x_i-\bar{x}_w)(y_i-\bar{y}_y)}{\left[\sum_{i=1}^nw_i(x_
i-\bar{x}_w)^2\right ]^{1/2} \left [ \sum_{i=1}^n w_i(y_i-\bar{y}_w)^2 \right ]^{1/2} } $$
가중 상관 계수는 가중치가 낮은 데이터에는 덜 영향을 받고 가중치가 높은 데이터 위주로 상관성을 보게된다. 이에 대한 실험을 해보자. 20개 데이터를 생성했고 $x_i$은 1부터 20까지 부여하고 $y_i$ 표준균등분포에서 랜덤하게 생성했다. 이때 가중치 $w_i$는 데이터 평균($\bar{x}, \bar{y}$)을 중심으로 좌하단과 우상단 영역의 데이터 가중치를 크게 주었다. 또한 직선을 추가하기 위해 최소 제곱 단순 회귀 모형과 가중 최소 제곱 단순 회귀 모형을 적합하였다.
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False
def cov(x, y, weight=None):
if weight is None:
return np.cov(x, y)[0,1]
return mean((x-mean(x, weight))*(y-mean(y, weight)), weight)
def corr(x, y, weight=None):
if weight is None:
return np.corrcoef(x, y)[0,1]
return cov(x, y, weight)/np.sqrt(cov(x, x, weight)*cov(y, y, weight))
from sklearn.linear_model import LinearRegression
np.random.seed(100)
size = 20
x = np.arange(size)+1
y = np.random.rand(size)
X = np.expand_dims(x, axis=1)
reg = LinearRegression().fit(X, y) ## 단순 최소 제곱 회귀 모형
reg1 = LinearRegression().fit(X, y, sample_weight=weight) ## 단순 가중 최소 제곱 회귀 모형
## 데이터 평균을 중심으로 좌하단 부분과 우상단 부분은 큰 가중치
weight = np.zeros(size)
left_y_mean = np.mean(y[x<=10])
right_y_mean = np.mean(y[x>10])
weight = np.ones(size)*5
lower_left_idx = np.where((x<=10)&(y<=left_y_mean))[0]
upper_right_idx = np.where((x>10)&(y>=right_y_mean))[0]
weight[upper_right_idx] = np.random.randint(50, 100, len(upper_right_idx))
weight[lower_left_idx] = np.random.randint(50, 100, len(lower_left_idx))
m1 = corr(x, y)
m2 = corr(x, y, weight)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(x, y, s=weight, label='data')
plt.plot(x, reg.predict(X), linestyle='--', color='k', label=f'상관계수({m1:.3f})')
plt.plot(x, reg1.predict(X), linestyle='--', color='r', label=f'가중 상관계수({m2:.3f})')
plt.legend()
plt.show()
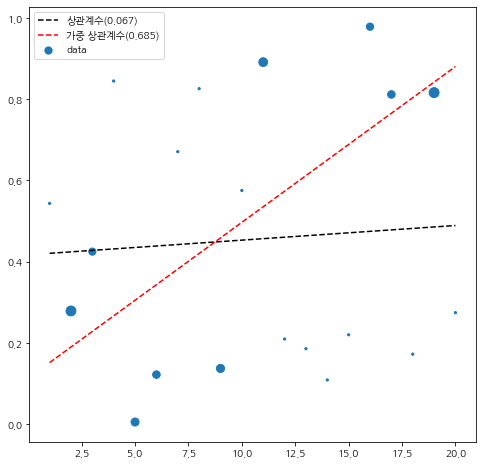
검은 점선을 보면 일반 상관 계수는 그렇게 강한 직선 관계를 보이지 않으나 가중치를 반영하니 강한 양의 상관 관계(빨간 점선)가 나타나는 것을 알 수 있다.
4. 가중 분위수(Weighted Quantile)
데이터와 가중치 $x_i, w_i$에 대하여 $x_i$가 오름차순으로 정렬되어 있다고 해보자. 이때 샘플 $p$-가중 분위수 $x_w^p$는 다음을 만족하는 데이터 $x_k$를 말한다.
$$\sum_{i=1}^{k-1}w_i \leq p \\ \sum_{i=k+1}^nw_i \geq 1-p$$
가중 분위수를 실험해보자. 나는 일반 중앙값과 가중 중앙값을 비교하고자 하였다. 가중 분위수 계산 함수는 위키를 참고하였다.
import numpy as np
import matplotlib.pyplot as plt
def weighted_quantile(x, quantile, weight=None):
if weight is None:
weight = np.ones(len(x))
weight = np.array(weight)
sort_idx = np.argsort(x)
x = x[sort_idx]
weight = weight[sort_idx]
weighted_quantiles = np.cumsum(weight) - 0.5 * weight
weighted_quantiles /= np.sum(weighted_quantiles)
cum_sum_weight = np.cumsum(weighted_quantiles)
if len(np.where(cum_sum_weight >= quantile)[0]) == 0:
idx = len(x) - 1
else:
idx = np.min(np.where(cum_sum_weight >= quantile)[0])
if idx == 0:
return x[0]
else:
x1 = cum_sum_weight[idx]
y1 = x[idx]
m = (x[idx]-x[idx-1])/(cum_sum_weight[idx]-cum_sum_weight[idx-1])
linear_func = lambda x: m*(x-x1)+y1
return linear_func(quantile)
np.random.seed(100)
size = 20
data = np.random.randint(0, 100, size)
## 평균보다 작은 곳은 작은 가중치 큰 곳은 큰 가중치
weight = np.zeros(size)
lower_idx = np.where(data<=np.mean(data))[0]
weight[lower_idx] = np.random.randint(5, 20, len(lower_idx))
upper_idx = np.where(data>np.mean(data))[0]
weight[upper_idx] = np.random.randint(50, 100, len(upper_idx))
fig = plt.figure(figsize=(10,6))
fig.set_facecolor('white')
plt.scatter(range(len(data)), data, s=weight, label='data')
plt.axhline(np.median(data), linestyle='--', label='중앙값', color='k')
plt.axhline(weighted_quantile(data, 0.5, weight), linestyle='--', label='가중 중앙값', color='r')
plt.xticks(range(len(data)), [str(i+1) for i in range(len(data))])
plt.legend()
plt.show()

일반적인 중앙값과 달리 가중 중앙값 또한 가중치가 높은 데이터를 잘 반영하여 위로 쏠리는 것을 알 수 있다.
5. 가중치 통계량의 장단점
- 장점 -
a. 각 데이터 별 가중치를 반영하여 합리적인 통계량을 제공할 수 있다.
가중치 데이터가 있는 경우 가중치가 낮은 데이터는 무시하고 가중치가 높은 데이터에 더 집중하여 통계량을 계산하는 것이 더 합리적이라는 것이다.
b. 기존 방식으로는 보이지 않았던 패턴이 가중치를 이용하면 명확한 패턴을 찾을 수 있다.
c. 일반적으로 이상치에 덜 민감할 수도 있다.
만약 이상치에 대해서 가중치를 적게 준다면 가중치 통계량은 이상치에 덜 민감할 수 있다.
d. 구현이 쉽다.
- 단점 -
a. 어떤 가중치가 더 좋은 것인지 판단하는 작업이 필요하며 상황에 따라 주관적으로 결정되어야 한다.
가중치 $w_i$가 있는 경우 생각해볼 수 있는 새로운 가중치$w^{(*)}_i$가 다음과 같다고 해보자.
$$w^{(*)}_i = (w_i)^q$$
$q=1$인 경우 기존 가중치를 쓰겠다는 것이다. 이때 $0<q<1$이면 큰 가중치에 대해서 많이 늘어나지 않는 가중치를 주는 것이며 $q>1$인 경우 기존 가중치가 큰 값인 경우에 대해 더 큰 가중치를 주겠다는 것이다.
이때 어떤 가중치가 좋은지 결정하는 과정이 필요하다. 만약 지도 학습의 경우 가중 최소 제곱을 이용하여 $R^2$가 높은 가중치를 선택할 수도 있을 것이다. 하지만 $y$가 없는 경우에는 주관적인 판단으로 가중치를 정해야 할 것이다.
b. 가중치가 적절하지 않은 경우에는 이상치에 민감할 수 있다.
가중치를 작게하여 영향을 줄이는 효과에 비해 이상치가 매우 크다면 가중 평균, 가중 상관 계수 역시 이상치에 영향을 받을 수 있다. 또한 특정 데이터 포인트에 가중치가 몰려 있는 경우 가중 분위수가 급격하게 변하여 해석이 어려울 수 있다.
'통계 > 기타' 카테고리의 다른 글
| ANOVA(Analysis of Variance, 분산분석)에 대해서 알아보자. (7) | 2022.12.06 |
|---|---|
| 통계학이란 무엇인가? (0) | 2022.11.07 |
| Profile Likelihood 란 무엇인가?! (408) | 2022.04.30 |
| 가설 검정과 P Value(유의 확률)에 대하여 알아보자. (1049) | 2021.09.20 |
| 자유도에 대해서 정확하게 파헤쳐 보자! (2) | 2020.08.23 |





댓글