이번 포스팅에서는 ANOVA(Analysis of Variance, 분산분석)의 개념과 One Way ANOVA(일원분산분석), Two Way ANOVA(이원분산분석)에 대해서 복습하고 정리해보았다.
- 목차 -
1. ANOVA(Analysis of Variance)
1. ANOVA(Analysis of Variance)
1) 정의
ANOVA는 ANalysis Of VAriance의 준말로 관심의 대상이 되는 변수에 대한 변동성의 원천을 통계적 모델링으로 분석하는 방법론을 의미한다.
2) 파헤치기
위에서 소개한 정의를 하나씩 파헤쳐보자.
a. ANOVA는 관심 변수의 변동성의 원천을 분석한다.
예를 들어 어떤 사람이 어떤 매장에서 신발을 산다고 해보자.

신발 가격을 살펴보면 일반적으로 가격이 제각각이다. 즉, 신발 가격은 변동성이 있는 것이다. ANOVA는 다음과 같은 질문에서 시작한다.
신발 가격 변동성은 무엇으로부터 발생한 것인가?
ANOVA는 관심 변수(신발 가격)의 변동성의 원인을 분석하게 된다.
b. ANOVA는 변동성 원인 분석을 위해 통계적 모델링을 사용한다.
돌아가서 위 질문에 대한 후보 원인들은 브랜드, 재료, 색상, 진열 위치, 운동화 성별 등이 있을 것이다. ANOVA는 이러한 원인을 통계적 모델링으로 설정하고 해당 원인이 실제로 변동을 발생시키는 유의한 인자인지 통계적 검정을 수행하여 판단한다. ANOVA는 일반적으로 원인 변수를 범주형으로 설정한다.
ANOVA는 원인 인자의 개수에 따라 One Way ANOVA, Two Way ANOVA로 분류할 수 있다. 각각에 대한 통계적 모델링 방법은 아래에서 다루기로 한다.
2. One Way ANOVA(일원분산분석)
1) 정의
먼저 $k$개의 그룹을 갖는 관측 데이터가 아래와 같이 설정되어 있다고 해보자.
$$X_{1, 1}, X_{1, 2}, \ldots, X_{1, n_1}, \ldots, X_{k, 1}, X_{k, 2}, \ldots, X_{k, n_k}$$
이제 관측 데이터를 다음과 같이 모델링한다.
$$X_{i, j} = \mu + \alpha_i + e_{i, j}, \;\; i=1, \ldots, k, \;\; j=1, \ldots, n_i \tag{1}$$
여기서 $\mu$는 그룹에 관계없는 관측 데이터의 공통 평균을 나타낸다. 그리고 $\alpha_i$는 그룹 특화된 효과를 나타내며 마지막으로 $e_{i, j}$은 예측할 수 없는 오차를 나타낸다. 그룹 특화된 효과를 보통 처리 효과(Treatment Effect)라 부른다.
One Way ANOVA는 관심 변수의 변동성을 하나의 원인으로부터 발생한다고 가정한다. 그래서 (1)과 같은 모델링으로 표현하며 그룹 특화된 효과(원인)를 검정함으로써 해당 효과가 관심 변수의 변동성을 만들어내는 원인인지 아닌지 판단하는 분석방법이다.
One Way ANOVA는 2가지 가정을 필요로 한다.
가정(Assumption)
1) $e_{i, j}$는 독립적으로 정규 분포 $\mathcal{N}(0, \sigma^2)$을 따른다.
2) $\sum_{i=1}^kn_i\alpha_i = 0$
가정의 고찰
1) One Way ANOVA는 기본적으로 그룹별 분산이 동일하다고 가정한다. 그리고 정규 분포를 가정하는 이유는 모수적(Parametric) 가설 검정을 유도하기 위한 것이다.
2) 모형 식별과 관련된 것이다. 식 (1)에서 $\mu$와 $\alpha_i$에 대한 추정량 $\hat{\mu}$, $\hat{\alpha}_i$를 얻었다고 해보자. 이때 $\hat{\mu}$, $\hat{\alpha}_i$이 정말 $\mu$와 $\alpha_i$의 추정량이라고 할 수 있을까?
아니다.
왜냐하면 임의의 상수 $c$에 대해서 아래의 등식이 성립하기 때문이다.
$$ \mu+\alpha_i = \mu-c + \alpha_i+c$$
이것이 무엇을 의미하냐 하면 $\hat{\mu}$, $\hat{\alpha}_i$이 $\mu, \alpha_i$의 추정량이 아닌 $\mu-c, \alpha_i+c$의 추정량이라고도 할 수 있기 때문이다. 이러한 애매모호함은 $\alpha_i$가 필요 이상으로 자유롭게 움직이기 때문에 생긴 것이며 따라서 이를 없애기 위하여 2)의 가정을 하는 것이다. 2)의 조건식을 통해 다음을 알 수 있다.
2)를 만족하는 두 파라미터 벡터 $(\mu_1, \alpha_{11}, \ldots, \alpha_{1k})$, $(\mu_2, \alpha_{21}, \ldots, \alpha_{2k})$가 있다고 하자. 이때 두 파라미터는 모형 (1)로부터 나온 추정량 벡터들이라고 생각하면 된다. 이때 2)를 만족하는 상황에서 이 두 파라미터 벡터가 같다면 우리는 각 추정량들이 타겟팅하는 모수가 유일하다고 할 수 있는 것이다.
$$\begin{align} \mu_1 + \alpha_{1i} = \mu_2 + \alpha_{2i} \;\; \forall i &\Rightarrow \mu_1\sum_{i=1}^kn_i + \sum_{i=1}^kn_i\alpha_{1i} = \mu_2\sum_{i=1}^kn_i + \sum_{i=1}^kn_i\alpha_{2i} \\ &\Rightarrow \mu_1\sum_{i=1}^kn_i = \mu_2\sum_{i=1}^kn_i \\ \Rightarrow \mu_1 = \mu_2 \end{align}$$
$\mu_1 = \mu_2$를 위 첫 번째 등식에 적용하면 모든 $i$에 대하여 $\alpha_{1i} = \alpha_{2i}$가 된다. 따라서 앞에서 논의한 애매한 상황은 일어나지 않게 된다.
2) 검정 방법
a. 귀무가설과 대립 가설
먼저 One Way ANOVA에서 검정하고자 하는 귀무가설과 대립 가설은 다음과 같다.
$$H_0 : \alpha_1 = \alpha_2 = \cdots = \alpha_k = 0 \;\;\text{ vs }\;\; H_a : \alpha_i \text{ not all zero}$$
귀무가설 $H_0$는 그룹 특화된 효과가 없다는 것이며 대립 가설 $H_a$은 적어도 한 그룹에서는 그룹 특화 효과가 있다는 것이다.
b. 검정 통계량
먼저 $\mu$와 $\alpha_i$의 최적 추정량은 다음과 같다(여기서 최적 추정량의 의미는 전역 최소 분산 불편 추정량 (Uniform Minimum Variace Unbiased Estimator : UMVUE)를 의미하는데 이에 대한 설명은 나중에 따로 포스팅하겠다).
$$\begin{align} \hat{\mu} &= \sum_{i=1}^kn_i\hat{\alpha}_i/\sum_{i=1}^kn_i \\ \hat{\alpha}_i &= \sum_{j=1}^{n_i}X_{i, j}/n_i -\hat{\mu} = \bar{X}_i-\hat{\mu} \end{align}$$
그리고
$$SSB = \sum_{i=1}^kn_i\hat{\alpha}_i^2 = \sum_{i=1}^kn_i(\bar{X}_i-\hat{\mu})^2, \;\; \\ SSW = \sum_{i=1}^k\sum_{j=1}^{n_i}(X_{i,j}-\hat{\mu}-\hat{\alpha}_i)^2 = \sum_{i=1}^k\sum_{j=1}^{n_i}(X_{i,j}-\bar{X}_i)^2$$
라하자.
$SSB$는 그룹 간(Between Group) 변동을 $SSW$는 그룹 내(Within Group) 변동을 의미한다.
One Way ANOVA에서 검정 통계량은 다음과 같다.
$$F = \frac{SSB/(k-1)}{SSW/(n-k)}$$
검정 통계량 고찰
검정 통계량 $F$가 나오게 된 배경을 알아보고자 한다. 먼저 $SSB$ 값이 커지면 귀무가설 $H_0$를 기각할 가능성이 높아지는 것을 알 수 있다. 따라서 $SSB$를 분자에 두어 그 값이 커지면 기각할 수 있는 검정 통계량을 만들어 준 것이다. 하지만 $SSB$는 상대적으로 비교해야 한다. 왜냐하면 $SSB$가 진짜 큰지 알 수 없기 때문이다. 이때 $SST$를 다음과 같이 정의하자.
$$SST = \sum_{i=1}^k\sum_{i=1}^{n_i}(X_{i, j} - \hat{\mu})^2$$
여기서 $SST$는 (공통 평균 대비) 총변동이라 할 수 있다. 따라서 검정 통계량 $F$를 다음과 같이 생각해볼 수 있다.
$$F' = \frac{SSB}{SST}$$
하지만 $F'$은 귀무가설이 참일 때 확률 분포를 계산하기 어렵다. 따라서 다른 통계량을 찾아야 한다. 이때 간단한 계산을 통해 다음을 알 수 있다.
$$SST = SSB+SSW$$
이를 이용하면
$$\frac{SSB}{SST} = \frac{SSB}{SSB+SSW} = \frac{SSB/SSW}{SSB/SSW+1}$$
임을 알 수 있다.
이때 $SSB/SSW$가 커지면 $SSB/SST$도 커짐을 알 수 있다. 따라서 큰 값을 가질 때 기각할 수 있는 통계량으로 $SSB/SSW$은 적절하다. 또한 앞에 양수를 곱해도 상관없다.
$$F = \left ( \frac{n-k}{k-1} \right ) \frac{SSB}{SSW} $$
이때 F는 통계 이론으로부터 귀무가설이 참일 때 분자의 자유도는 $k-1$, 분모의 자유도는 $n-k$인 $F$ 분포를 따르는 것이 알려져 있다.
c. 기각역
One Way ANOVA에서 유의 수준이 $\alpha$일 때 기각역은 다음과 같다.
$$F \geq F_{\alpha}(k-1, n-k)$$
$F_{\alpha}(k-1, n-k)$은 분자의 자유도는 $k-1$, 분모의 자유도는 $n-k$인 $F$ 분포에서 오른쪽 꼬리값이 $\alpha$가 되게 하는 값이다.
3) 예제
개념은 알았으니 예제를 통해서 One Way ANOVA를 수행해보자. 먼저 아래와 같이 3가지 학습 방법에 따른 국어 평가 점수가 다음과 같다고 할 때 학습 방법에 따라 실제로 성적 차이가 있는지 One Way ANOVA를 이용하여 확인해보자.

먼저 여기서 검정하고자 하는 귀무가설과 대립 가설은 다음과 같다.
$H_0 : $ 세 학습 방법에 따른 국어 성적 차이는 없다.
$H_a : $ 학습 방법에 따른 국어 성적 차이가 있다.
이 경우 $k=3, n_1 = 10, n_2 = 8, n_3 = 9, n = n_1+n_2+n_3 = 27$이다. 또한 전체 평균과 그룹 평균은 다음과 같다.
$$\begin{align} & \bar{x} = \frac{1}{n}\sum_{i=1}^k\sum_{j=1}^{n_i} x_{i, j} = 6.7 \\ & \bar{x}_1 = \frac{1}{n_1}\sum_{j=1}^{n_1}x_{1j} = 7.5, \bar{x}_2 = 5.25, \bar{x}_3 = 7.11 \end{align}$$
이제 총 변동 $SST$, 그룹 간 변동 $SSB$와 그룹 내 변동 $SSW$를 구해보자.
$$SST = \sum_{i=1}^k\sum_{j=1}^{n_i}(x_{i, j}-\bar{x})^2 = 61.63 \\ SSB =\sum_{i=1}^kn_i(\bar{x}_i-\bar{x})^2 = 24.74 \\ SSW = \sum_{i=1}^k \sum_{j=1}^{n_i}(x_{i, j}-\bar{x}_i)^2 = 36.89$$
그리고 분자의 자유도는 $k-1 = 2$, 분모의 자유도 $n-k=24$이다. 따라서 검정 통계량 $F$는 다음과 같이 계산할 수 있다.
$$F = \frac{MSB}{MSW} = \frac{SSB/(k-1)}{SSW/(n-k)}$$
그리고 유의 수준 $\alpha = 0.05$에 대한 기각값 $F_{0.05}(2, 24) = 3.40$이다. 이제 다음의 테이블을 정리할 수 있다(ANOVA Table이라고도 한다).

한편
$$F = 8.05 > 3.40 = F_{0.05}(2, 24) = 3.40$$
이므로 귀무가설은 기각되며 세 학습 방법에 따른 성적의 차이가 존재한다고 볼 수 있다.
3. Two Way ANOVA(이원분산분석)
1) 정의
두 개의 인자(범주형 변수) $A, B$가 각각 $a$개, $b$개의 수준이 있고 두개의 수준 조합별로 관심 변수 $X$가 $r$개 관측되었다고 해보자(이를 균형 있는 설계(Balanced Design)이라 한다).
이 경우 아래의 모델링을 생각해 볼 수 있다.
$$X_{ijk} = \mu+ \alpha_i + \beta_j +\gamma_{ij}+e_{ijk}, i=1, \ldots, a, j=1, \ldots, b, k=1, \ldots, r \tag{2}$$
$\mu$는 처리 수준과 관계없는 공통 평균을 나타내며 $\alpha_i$는 $A$인자에 대한 처리 효과, $\beta_j$는 $B$인자에 대한 처리 효과라 한다. 그리고 $\gamma_{ij}$는 $A$의 $i$번째, $B$의 $j$번째 처리 조합 효과 중에서 처리 주 효과 설명할 수 없는 효과를 나타낸 것으로 달리 말하면 $A$의 $i$번째, $B$의 $j$번째 처리효과가 합쳐서 나타난 시너지 효과라 볼 수 있으며 이를 통계학에선 교호 작용효과(Interaction Effect)라고 한다.
One Way ANOVA는 관심 변수의 변동성을 하나의 원인으로부터 발생한다고 가정하는 것과 달리 Two Way ANOVA는 두 개의 원인 인자(범주형 변수)가 관심 변수의 변동성을 유발한다고 가정한다. 그래서 (2)와 같은 모델을 이용하며 두 인자의 처리 효과를 통계적으로 검정하여 실제로 두 인자가 관심 변수의 변동성을 발생시키는지 확인하는 분석 방법이다.
Two Way ANOVA 또한 두 가지 가정을 필요로 한다.
가정(Assumption)
1) $e_{ijk}$는 독립적으로 $\mathcal {N}(0, \sigma^2)$을 따른다.
2) 모형 (2)는 아래의 제약식을 만족한다.
$$\sum_{i=1}^a\alpha_i = 0, \sum_{j=1}^b\beta_j=0, \sum_{i=1}^a\gamma_{ij} = 0, \sum_{j=1}^b\gamma_{ij} = 0$$
가정 1)은 모수적(Parametric) 검정을 유도하기 위한 것이며 2)는 모형 식별을 위한 것이다.
2) 검정 방법
a. 귀무가설과 대립 가설
Two Way ANOVA는 세 가지 귀무 가설과 대립 가설을 검정한다.
먼저 $A$인자 처리 효과에 대한 가설이다.
$$ H_0 : \alpha_i = 0 \;\;\forall i=1, \ldots, a \text{ vs } H_a : \text{not } H_0 \tag{H1}$$
다음으로 $B$인자 처리 효과에 대한 가설이다.
$$ H_0 : \alpha_j = 0 \;\;\forall j=1, \ldots, b \text{ vs } H_a : \text{not } H_0 \tag{H2}$$
마지막으로 교호 작용효과에 대한 가설이다.
$$ H_0 : \gamma_{ij} = 0 \;\;\forall i, j \text{ vs } H_a : \text{not } H_0 \tag{H3}$$
b. 검정 통계량
먼저 각 모수의 추정량은 다음과 같다.
$$\begin{align} \hat{\mu} &= \sum_{i,j,k} X_{ijk}/abr = \bar{X}_{...} \\ \hat{\alpha}_i &= \sum_{j=1}^b\sum_{k=1}^rX_{ijk}/br - \hat{\mu} = \bar{X}_{i..} - \bar{X}_{...} \\ \hat{\beta}_j &= \sum_{i=1}^a\sum_{k=1}^rX_{ijk}/ar - \hat{\mu} = \bar{X}_{.j.} - \bar{X}_{...} \\ \hat{\gamma}_{ij} &= \sum_{k=1}^rX_{ijk}/r - \bar{X}_{i..} - \bar{X}_{.j.} + \bar{X}_{...} = \bar{X}_{ij.} - \bar{X}_{i..} - \bar{X}_{.j.} + \bar{X}_{...} \end{align}$$
이제 (H1), (H2), (H3)을 검정하는 검정 통계량을 살펴보자.
$$\begin{align}SSE &= \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r(X_{ijk}-\bar{X}_{ij.})^2 \\ SSA &= \sum_{i=1}^abr(\bar{X}_{i..}-\bar{X}_{...})^2 \\ SSB&=\sum_{j=1}^bar(\bar{X}_{.j.}-\bar{X}_{...})^2 \\ SSAB &= \sum_{i=1}^a\sum_{j=1}^br(\bar{X}_{ij.}-\bar{X}_{i..}-\bar{X}_{.j.}+\bar{X}_{...})^2\end{align}$$
(H1)을 검정하기 위한 검정 통계량은 다음과 같다.
$$F_1 = \frac{SSA/(a-1)}{SSE/(n-ab)}$$
(H2)을 검정하기 위한 검정 통계량은 다음과 같다.
$$F_2 = \frac{SSB/(b-1)}{SSE/(n-ab)}$$
(H3)을 검정하기 위한 검정 통계량은 다음과 같다.
$$F_3= \frac{SSAB/\{(a-1)(b-1)\} }{SSE/(n-ab)}$$
교호 작용효과 추정량의 고찰
교호작용효과 $\gamma_{ij}$는 $A$의 $i$번째 $B$의 $j$번째 처리 조합 효과에서 처리 주 효과로 설명되지 않는 부분이라고 하였다. 이를 관측 데이터로 추정한다고 해보자. 먼저 $A$의 $i$번째 $B$의 $j$번째 처리 조합 (순수) 효과는 다음과 같이 추정할 수 있다.
$$ \bar{X}_{ij.} - \bar{X}_{...}$$
즉, 공통 평균에서 $A$의 $i$번째 $B$의 $j$번째 처리 조합을 동시에 고려했을 때 변동되는 부분이 바로 처리 조합 효과인 것이다. 같은 방식으로 $A$의 $i$번째 처리 주 효과와 $B$의 $j$번째 처리 주 효과는 다음과 같다.
$$ \bar{X}_{i..} - \bar{X}_{...}, \bar{X}_{.j.}-\bar{X}_{...}$$
교호 작용효과는 처리 조합 효과에서 각 처리 주효 과로 설명되지 않는 부분이므로 다음과 같이 나타낼 수 있다.

그리고 위 식 우변을 계산하면 다음과 같이 교호 작용효과의 추정량이 되는 것이다.
$$\hat{\gamma}_{ij} = \bar{X}_{ij.}-\bar{X}_{i..}-\bar{X}_{.j.}+\bar{X}_{...}$$
ANOVA 공부할 때 교호 작용효과에 대한 추정량의 모양이 잘 이해가 가지 않아서 고생했던 기억이 있다.
c. 기각역
유의 수준 $\alpha$에 대하여 (H1)의 기각역은 다음과 같다.
$$F_1 \geq F_{\alpha}(a-1, n-ab)$$
(H2)의 기각역은 다음과 같다.
$$F_2 \geq F_{\alpha}(b-1, n-ab)$$
(H3)의 기각역은 다음과 같다.
$$F_3 \geq F_{\alpha}((a-1)(b-1), n-ab)$$
2) 예제
이제 예제를 통해서 Two Way ANOVA를 수행해보자. 어떤 약품의 흡수 속도는 촉매량($A$)과 반응 온도($B$)에 따라 달라진다고 추측하고 있다. 이때 촉매량은 4가지 수준, 반응 온도는 3가지 수준에서 약품의 흡수 속도를 관측한 결과 다음과 같은 자료를 얻었다.
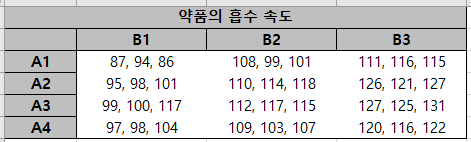
이 문제에서 $a=4, b=3, r=3$이다. 그리고 필요한 통계량을 계산해보자.
$$\begin{align} SSE &= \sum_{i=1}^a\sum_{j=1}^b\sum_{k=1}^r(X_{ijk}-\bar{X}_{ij.})^2 = 459.33 \\ SSA &= \sum_{i=1}^abr(\bar{X}_{i..}-\bar{X}_{...})^2 = 977.64 \\ SSB&=\sum_{j=1}^bar(\bar{X}_{.j.}-\bar{X}_{...})^2 = 3267.56 \\ SSAB &= \sum_{i=1}^a\sum_{j=1}^br(\bar{X}_{ij.}-\bar{X}_{i..}-\bar{X}_{.j.}+\bar{X}_{...})^2 = 87.78 \end{align}$$
이제 검정 통계량을 계산해보자.
$$\begin{align} F_1 &= \frac{SSA/(a-1)}{SSE/(n-ab)} = \frac{325.88}{19.14} = 17.03 \\ F_2 &= \frac{SSB/(b-1)}{SSE/(n-ab)} = \frac{1633.78}{19.14} = 85.36 \\ F_3 &= \frac{SSAB/\{(a-1)(b-1)\} }{SSE/(n-ab)} = \frac{14.63}{19.14} = 0.76 \end{align}$$
그리고 유의 수준 0.05에서 $F_1, F_2, F_3$의 기각 값(Critical value)는 각각
$$F_{0.05}(3, 24) = 3.01, F_{0.05}(2, 24) = 3.40, F_{0.05}(6, 24) = 2.51$$
이다.
이제 Two Way ANOVA Table을 만들 수 있다.

$$F_1 = 17.03 > 3.01, F_2 = 85.36 >3.4$$
이므로 약품 흡수 속도는 촉매량과 반응 온도에 따라 각각 달라진다고 할 수 있다. 하지만
$$F_3 = 0.76 < 2.51$$
이므로 촉매량과 반응 온도의 교호 작용효과가 있다고 보긴 어렵다.
4. ANOVA 장단점
- 장점 -
a. T-Test는 2 그룹 간 평균 비교를 검정하는 반면 ANOVA는 3개 이상의 그룹 간 평균 비교가 가능하다.
b. 제곱합 계산만 해주면 되므로 검정 방법이 간단하다.
- 단점 -
a. 오차의 분포가 정규 분포가 아닌 경우 사용할 수 없다.
b. 처리 수준 또는 처리 조합별로 오차의 등분산성이 현실적이지 않으며 등분산 가정이 깨지는 경우 ANOVA 결과를 신뢰할 수 없다.
c. 대립 가설이 구체적이지 않다.
대립 가설은 그룹 간 처리효과가 없지 않다는 것이며 실제로 어떤 그룹이 처리 효과가 있는지를 알려주지 않는다.
d. 독립성, 정규성, 오차의 등분산성 가정을 확인하는 작업이 필요하고 그 과정도 어렵다고 한다.
- 참고 자료 -
수리통계학 - 김우철
One Way Analysis of Variance ANOVA Unbalaced Design - Youtube
'통계 > 기타' 카테고리의 다른 글
| 특이값 분해(Singular Value Decomposition : SVD)에 대해서 알아보자(feat. Numpy) (0) | 2023.03.07 |
|---|---|
| 고유값과 고유 벡터 그리고 고유값 분해(Eigen Decomposition)에 대해서 알아보자 (feat. Numpy) (2) | 2023.03.04 |
| 통계학이란 무엇인가? (0) | 2022.11.07 |
| 가중치를 활용한 통계량을 알아보자. 가중 평균(Weighted Mean), 가중 상관계수(Weighted Correlation), 가중 분위수 (Weighted Quantile) (2) | 2022.09.25 |
| Profile Likelihood 란 무엇인가?! (408) | 2022.04.30 |





댓글