이번 포스팅에서는 Box-Cox Transformation(변환)에 대한 개념과 파이썬(Python)을 이용하여 어떻게 구현하는지 알아본다. 그리고 실제 데이터에 적용하여 Box - Cox Transformation(변환)이 어떻게 사용되는지 살펴보자.
여기서 다룰 내용은 다음과 같다.
1. Box-Cox Transformation(변환)이란?
2. Box-Cox Transformation(변환) 모수 추정
3. Box-Cox Transformation(변환) 장단점
이 곳은 꽁냥이가 머신러닝을 공부한 내용을 정리하는 곳입니다.
이 포스팅에서는 수식을 포함하고 있습니다. 티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니 웹브라우저 또는 모바일 웹브라우저로 보시길 바랍니다.
1. Box-Cox Transformation(변환)이란?
- 배경 -
우리가 선형 회귀 분석을 하는 데 있어 반응 변수가 정규분포라는 가정을 기본적으로 하게 된다. 하지만 정규분포가 아닌 경우가 꽤 많다. Box와 Cox는 반응 변수를 적절한 비선형 변환을 통해 정규성을 확보할 수도 있다고 주장했다.
- 정의 -
1) One Parameter Box-Cox Transformation(변환)
양수인 반응 변수 벡터 $y = (y_1, \ldots, y_n)^t$에 대하여 Box-Cox Transformation(변환)은 $y_i(\lambda)$ 다음과 같이 정의된다.
$$y_i(\lambda) = \begin{cases} \frac{y_i^\lambda-1}{\lambda} & \text{ if } \lambda \neq 0 \\ \log y_i & \text{ if } \lambda = 0 \end{cases} \tag{1}$$
$$\lim_{\lambda \rightarrow 0} \frac{y^\lambda-1}{\lambda} = \log y$$
이므로 $y_i(\lambda)$는 모든 실수 $\lambda$에 대하여 연속인 변환이다.
하지만 $\lambda$에 따른 반응 변수의 단위를 보존하고 로그 우도 함수의 간결성을 위하여 반응 변수의 조화 평균
$$GM(y) = (y_1\cdot y_2 \cdots \cdot y_n)^{1/n}$$
을 도입하여 다음과 같이 Box-Cox Transformation(변환)을 다시 정의한다.
$$y_i(\lambda) = \begin{cases} \frac{y_i^\lambda-1}{\lambda GM(y)^{\lambda - 1}} & \text{ if } \lambda \neq 0 \\ GM(y)\log y_i & \text{ if } \lambda = 0 \end{cases} \tag{2}$$
2) Two Parameter Box-Cox Transformation(변환)
앞에서는 양수인 반응 변수 벡터를 다루었는데 음수인 경우에 대해서도 (모수 하나를 추가로 도입하면) Box-Cox Transformation(변환)을 확장시킬 수 있다.
식 (2)를 확장하여 정의하면 다음과 같다.
$$y_i(\lambda_1, \lambda_2) = \begin{cases} \frac{(y_i+\lambda_2)^{\lambda_1}-1}{\lambda_1 GM(y+\lambda_2)^{\lambda_1 - 1}} & \text{ if } \lambda_1 \neq 0 \\ GM(y+\lambda_2)\log (y_i+\lambda_2) & \text{ if } \lambda_1 = 0 \end{cases} \tag{3}$$
여기서
$$GM(y+\lambda_2) = \left [ (y_1+\lambda_2)\cdot (y_2+\lambda_2) \cdots \cdot (y_n+\lambda_2) \right ]^{1/n}$$
이다. 이때 $y_i+\lambda_2 > 0 \text{ } \forall i$임을 만족해야 하므로 $\lambda_2>-\min_i y_i$라는 제약 조건이 생긴다.
2. Box-Cox Transformation(변환) 모수 추정
1. $\lambda_2 = 0$인 경우
a. 점추정
먼저 (1)의 경우에 대해서 $\lambda$를 추정하는 방법을 알아보자. 먼저 $y(\lambda) = (y_1(\lambda, \ldots, y_n(\lambda)))$는 정규분포를 가정한다. 즉, 설명 변수 행렬(Design Matrix) $X$가 주어졌고 선형 회귀 모형을 적용하는 경우
$$f(y(\lambda)) = (2\pi\sigma^2)^{-n/2}\exp \left ( -\frac{(y-X\beta)^t(y-X\beta)}{2\sigma^2} \right )\tag{4}$$
하지만 우리가 실제로 관측한 반응 변수는 $y$이므로 $y$의 로그 우도 함수를 구하기 위해 $y$의 밀도 함수 $f(y)$를 계산해야 한다. (4)를 이용하면
$$f(y) = (2\pi\sigma^2)^{-n/2}\exp \left ( -\frac{(y-X\beta)^t(y-X\beta)}{2\sigma^2} \right )J \tag{5}$$
임을 알 수 있다. 여기서 $J$는 $y$에서 $y(\lambda)$로의 변환에 대한 자코비안(Jacobian)이며 그 값은 다음과 같다.
$$J = \prod_{i=1}^n y_i^{\lambda - 1}$$
여기서 우리가 관심 대상은 $\lambda$이며 $\beta, \sigma^2$은 nuisance 모수이다. 따라서 Profile Likelihood 추정법을 써서 $\lambda$의 최대 우도 추정값을 구한다. Profile Likelihood 추정에 대한 설명은 여기에 포스팅해두었으니 참고하기 바란다.
먼저 $\lambda$를 고정시켜놓고 $\beta, \sigma$의 최대 우도 추정량은 다음과 같이 계산된다.
$$\hat{\beta} (\lambda) = (X^tX)^{-1}X_ty(\lambda) \\ \text{ } \\ \hat{\sigma}^2(\lambda) = \frac{(y(\lambda)-X\hat{\beta} (\lambda))^t (y(\lambda)-X\hat{\beta} (\lambda))}{n} = \frac{y(\lambda)^t(I_n-G)y(\lambda)}{n}\tag{6}$$
이때 $G = (X^tX)^{-1}X_t$이다.
(6)에서 계산된 값을 (5)에 대입하여 로그를 취하면 Profile Likelihood를 다음과 같이 얻을 수 있다.
$$l(\lambda) = C - \frac{n}{2}\log \hat{\sigma}^2(\lambda) + (\lambda -1) \sum_{i=1}^n \log y_i \tag{7}$$
여기서 $C$는 모수와 관계없는 상수이다.
이때 $y(\lambda)$를 $y(\lambda)/GM(y)$로 변형하여 (7)을 계산하면 즉 (2)의 Box-Cox Transformation을 이용하면 다음과 같다.
$$l(\lambda) = C-\frac{n}{2}\log s_\lambda^2\tag{8}$$
여기서 $s_\lambda^2$은 반응 변수를 (2)로 변환했을 때 선형 회귀 모형을 적합해서 얻은 잔차 제곱합에서 데이터 개수 $n$을 나눠준 값이다. 변환 (2)의 장점이 여기서 나오는 것이다.
최대 우도 추정량 $\hat{\lambda}$는 (8)을 최대화하는 값이며 수치적인 방법을 이용하여 계산한다.
b. 구간 추정
$\lambda$에 대한 구간 추정은 로그 우도비 통계량이 점근 카이제곱 분포를 따른다는 사실을 이용한다.
$\lambda$에 대한 $(1-\alpha)$% 신뢰구간은 다음과 같이 계산된다.
$$\{ \lambda : l(\hat{\lambda}) - l(\lambda) \leq \frac{1}{2}\chi_1^2(1-\alpha) \}$$
여기서 $\chi_1^2(1-\alpha)$는 자유도가 1인 카이제곱 분포의 $(1-\alpha)$ 분위수이다.
2. $\lambda_2 \neq 0$인 경우
a. 점추정
$s^2(\lambda_1, \lambda_2)$를 반응 변수의 변환 (3)을 선형 회귀 모형으로 적합시켰을 때의 잔차 제곱합에서 데이터 개수 $n$을 나눈 값이라고 하자. $\lambda_1, \lambda_2$의 최대 우도 추정량은 다음의 로그 우도 함수 $l$을 최대화하는 값으로 한다.
$$l(\lambda_1, \lambda_2) = C -\frac{n}{2}\log s^2(\lambda_1, \lambda_2) \tag{9}$$
b. 구간 추정
(9) 최대화하는 $\lambda_1, \lambda_2$를 $\hat{\lambda}_1, \hat{\lambda}_2$라 하자. 이때 우리의 관심대상은 $\lambda_1$이며 이에 대한 $(1-\alpha)$% 신뢰 구간은 다음과 같이 계산한다.
$$\{ \lambda_1 : l(\hat{\lambda}_1, \hat{\lambda}_2) - l(\lambda_1, \hat{\lambda}_2) \leq \chi_2^2(1-\alpha) \}$$
여기서 $\chi_2^2(1-\alpha)$는 자유도가 2인 카이제곱 분포의 $(1-\alpha)$ 분위수이다.
3. Box-Cox Transformation(변환) 장단점
- 장점 -
반응 변수가 정규분포가 아닌 경우 Box-Cox Transformation(변환)을 통하여 반응 변수의 정규성을 만족시킬 수 있다.
- 단점 -
해석이 어렵다.
예를 들어 Box-Cox Transformation(변환) (2)에서 $\hat{\lambda} = 0.94$인 경우 반응 변수를 어떻게 해석해야 하는 가에 대한 문제가 생길 수 있다. 몇몇 통계학자들은 0.94 대신 해석을 위해 0.94와 가까운 정수 1로 대신하는 것이 좋다고 한다. 하지만 어떤 통계학자들은 정수로 바꾸지 않고 실제 최대 우도 추정값인 0.94를 쓴다고 한다.
4. 파이썬(Python) 구현
이제 파이썬(Python)을 이용하여 Box-Cox Transformation(변환)과 모수를 추정하는 함수를 구현해보자.
먼저 필요한 모듈을 임포트해준다.
import numpy as np
import pandas as pd
import statsmodels.api as sm
import warnings
import matplotlib.pyplot as plt
import matplotlib as mat
import scipy.optimize as so
from scipy.stats import chi2
mat.rcParams['axes.unicode_minus'] = False
warnings.filterwarnings('ignore')
다음으로 조화 평균을 계산하는 함수(get_gm), Box-Cox Transformation(변환)을 수행하는 함수(box_cox_transform) 그리고 로그 우도 함수값을 계산하는 함수(get_log_likelihood)를 정의한다.
이때 조화 평균을 계산 시 안정성(stability)을 위하여 로그를 취해준 뒤 exp함수를 적용하였다.
def get_gm(y):
temp = np.mean(np.log(y))
return np.exp(temp)
def box_cox_transform(y, lambda1, lambda2=0):
y = y+lambda2
gm = get_gm(y)
if lambda1 != 0:
bc_tr = (y**(lambda1)-1)/(lambda1*(gm**(lambda1-1)))
else:
bc_tr = gm*np.log(y)
return bc_tr
def get_log_likelihood(y, X, lambda1, lambda2):
n = len(y)
y = box_cox_transform(y, lambda1, lambda2)
lm = sm.OLS(y, X).fit()
resid = lm.resid
sse = np.sum(np.square(resid))
ll_val = -0.5*n*np.log(sse/n)
return ll_val
이제 모수 $\lambda_1, \lambda_2$의 점추정치와 신뢰구간을 계산하는 함수를 정의한다. 이때 신뢰구간을 계산하는 부분(line 32~)은 scipy.opimize.fsolve 함수가 해를 하나밖에 찾지 못하므로 $\lambda_1$의 초기값을 최대 우도 추정량보다 0.5 작게 하여 신뢰구간의 하한을 계산하고 반대로 0.5보다 크게 하여 신뢰구간의 상한을 구하도록 했다.
def get_box_cox_params_estimate(y, X, lambda1, alpha=0.05, est_lambda2=False):
def func1(lambda1, y, X, lambda2):
return -get_log_likelihood(y, X, lambda1, lambda2)
def func2(lambda_vec, y, X):
lambda1 = lambda_vec[0]
lambda2 = lambda_vec[1]
return -get_log_likelihood(y, X, lambda1, lambda2)
# estimate parameters
if est_lambda2 == False:
obj_func = func1
dof = 1
res = so.minimize(func1, -2, args=(y, X, 0))
pe_lambda1 = res['x'][0] # point estimator for lambda1(mle)
max_ll_val = get_log_likelihood(y, X, pe_lambda1, 0)
else:
obj_func = func2
dof = 2
res = so.minimize(func2, (-2, c+0.01), args=(y, X))
pe_lambda1 = res['x'][0] # point estimator for lambda1(mle)
pe_lambda2 = res['x'][1] # point estimator for lambda2(mle)
max_ll_val = get_log_likelihood(y, X, pe_lambda1, pe_lambda2)
chi_quantile = chi2.ppf(1-alpha, dof)
res_sol = res['x']
# get confidence interval
def func3(lambda1, y, X, lambda2):
return max_ll_val-0.5*chi_quantile-get_log_likelihood(y, X, lambda1, lambda2)
if est_lambda2 == False:
ci_res_upper = fsolve(func3, pe_lambda1+0.5, args=(y, X, 0))[0]
ci_res_lower = fsolve(func3, pe_lambda1-0.5, args=(y, X, 0))[0]
else:
ci_res_upper = fsolve(func3, pe_lambda1+0.5, args=(y, X, pe_lambda2))[0]
ci_res_lower = fsolve(func3, pe_lambda1-0.5, args=(y, X, pe_lambda2))[0]
return res_sol, (ci_res_lower, ci_res_upper)5. 실제 데이터 적용
여기서는 가솔린 소모량(리터 단위)에 따른 주행거리(킬로 단위)를 살펴보기 위한 데이터를 준비했다.
x가 가솔린 소모량이고 y가 주행거리이다.
df = pd.read_excel('../dataset/distance_gasoline.xlsx')
df.head()

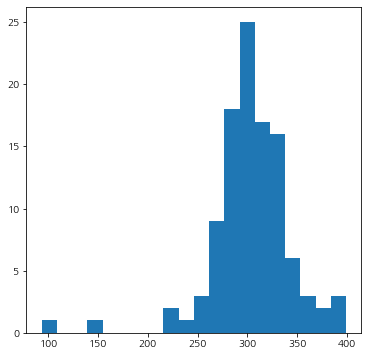
먼저 반응 변수의 분포가 정규분포랑 비슷한지 히스토그램을 그려서 확인해보자.
y = df['y']
fig = plt.figure(figsize=(6,6))
fig.set_facecolor('white')
plt.hist(y, bins=20)
plt.show()

왼쪽 꼬리가 길긴 한데 정규분포 모양도 보이긴 한다;;
1. One Parameter Box-Cox Transformation(변환)
이제 최적의 Box-Cox Transformation(변환)을 찾아보자. 먼저 변환 (2)인 경우 즉, One Parameter Box-Cox Transformation(변환)을 찾아보자.
result = get_box_cox_params_estimate(y, X, lambda1, alpha=0.05, est_lambda2=False)
mle_lambda = result[0][0]
confidence_interval = result[1]
print(f'MLE : {mle_lambda}, Confidence Interval : {confidence_interval}')

$\hat{\lambda} = 1.47$이며 95% 신뢰구간은 (0.71, 2.41)이다. 즉,
$$y_i(1.47) = (y_i^{1.47}-1)/(1.47(GM(y))$$
이 최적의 변환이다. 하지만 실제로 분석에 적용할 때에는 원한다면 $y_i(1.47)$이 아닌 $y_i^{1.47}$로 해도 된다고 한다.
이제 $y_i(1.47)$의 분포를 살펴보자.
y_trans = box_cox_transform(y, mle_lambda)
fig = plt.figure(figsize=(6,6))
fig.set_facecolor('white')
plt.hist(y_trans, bins=20)
plt.show()
기존 반응 변수의 분포(왼쪽)와 변환된 반응 변수의 분포(오른쪽)의 차이를 비교해보자. 오른쪽이 정규분포에 조금 더 가까워진 것 같다.

이번엔 최대 우도 추정량값이 1.47이라고 할 수 있는지 신뢰구간도 정확한지 시각적으로 확인해보자.
step=0.2
lambda1_list = np.arange(0, 3+step, step=step)
ll_val_list = []
for lambda1 in lambda1_list:
if abs(lambda1)<1e-5:
lambda1 = 0
ll_val = get_log_likelihood(y, X, lambda1, lambda2=0)
ll_val_list.append(ll_val)
fig = plt.figure(figsize=(6,6))
fig.set_facecolor('white')
plt.plot(lambda1_list, ll_val_list)
chi_quantile = chi2.ppf(0.95, 1)
max_ll_val = get_log_likelihood(y, X, mle_lambda, lambda2=0)
plt.axhline(max_ll_val-0.5*chi_quantile, linestyle='--', color='red')
plt.show()
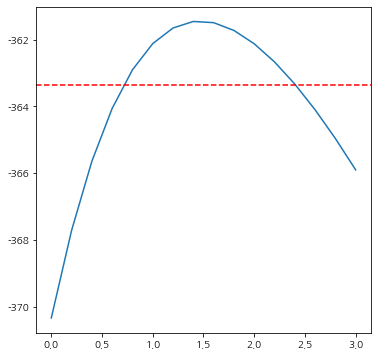
시각화 그래프를 통해 우리가 얻은 추정량과 신뢰구간이 정확하다는 것을 알 수 있다.
2. Two Parameter Box-Cox Transformation(변환)
이번엔 최적의 Two Parameter Box-Cox Transformation(변환)을 찾아보자.
result = get_box_cox_params_estimate(y, X, lambda1, alpha=0.05, est_lambda2=True)
mle_lambdas = result[0]
confidence_interval = result[1]
print(f'MLE : {mle_lambdas}, Confidence Interval : {confidence_interval}')

$\hat{\lambda}_1 = 1.28, \hat{\lambda}_2=-149.44$이며 $\lambda_1$의 95% 신뢰구간은 (0.76, 2.01) 임을 알 수 있다. 따라서 최적 Two Parameter Box-Cox Transformation(변환)은 다음과 같다.
$$y_i(1.28, -149.44) = (y_i-149.44)^{1.28}/(1.27GM(y-149.44))$$
이제 변환된 반응 변수의 분포를 살펴보자.
y_trans = box_cox_transform(y, mle_lambdas[0], mle_lambdas[1])
fig = plt.figure(figsize=(6,6))
fig.set_facecolor('white')
plt.hist(y_trans, bins=20)
plt.show()
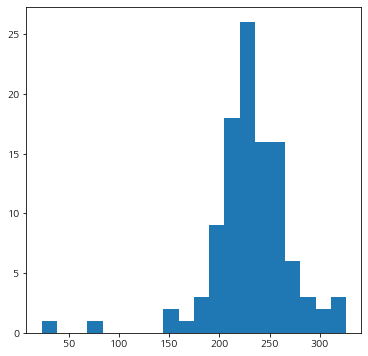
변환을 했더니 좀 더 정규분포에 가까워진 것 같다.
참고자료
Box-Cox Transformation: An Overview - https://www.ime.usp.br/~abe/lista/pdfm9cJKUmFZp.pdf
N R. Draper, Harry Smith - Applied Regression Analysis 3ed

'통계 > 머신러닝' 카테고리의 다른 글
| 15. AdaBoost(Adaptive Boost) 알고리즘에 대해서 알아보자 with Python (382) | 2022.05.06 |
|---|---|
| 14. 클러스터링(군집화) 평가지표 Silhouette(실루엣) 지수(계수)에 대해서 알아보자 with Python (410) | 2022.05.01 |
| 12. Gaussian Mixture Model(가우시안 혼합 모형) 클러스터링(군집 분석)에 대해서 알아보자 with Python (408) | 2022.04.25 |
| 12. 클러스터링(군집화) 평가 지표 Dunn Index with Python (401) | 2022.04.22 |
| 11. K-Means 클러스터링(Clustering, 군집화)에 대해서 알아보자 with Python (410) | 2022.04.21 |





댓글