이번 포스팅에서는 K-Means 클러스터링과 더불어 군집 분석에서 자주 사용되는 Gaussian Mixture Model 클러스터링(가우시안 혼합 모형 군집화)에 대해서 알아보고 파이썬(Python)으로 구현해보고자 한다.
1. Gaussian Mixture Model(가우시안 혼합 모형) 클러스터링이란?
2. Gaussian Mixture Model(가우시안 혼합 모형) 클러스터링 알고리즘
3. Gaussian Mixture Model(가우시안 혼합 모형) 클러스터링 장단점
4. Gaussian Mixture Model(가우시안 혼합 모형) 파이썬 구현
본 포스팅에서는 수식을 포함하고 있습니다.
티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니
PC 웹 브라우저 또는 모바일 웹 브라우저에서 보시기 바랍니다.
1. Gaussian Mixture Model(가우시안 혼합 모형) 클러스터링이란?
정의
Gaussian Mixture Model(GMM) 클러스터링은 클러스터(군집) 개수 $K$를 정하고 GMM을 이용하여 데이터 포인터들이 속하는 클러스터를 확률적으로 할당하는 Soft Clustering 알고리즘이다.
이 말의 뜻을 하나씩 살펴보자.
a. 클러스터(군집) 개수를 정해야 한다.
GMM 클러스터링 알고리즘은 K-Means 클러스터링 알고리즘과 마찬가지로 클러스터 개수 $K$를 사전에 정해줘야 한다. 자동적으로 정해지는 것이 아니다.
b. GMM 클러스터링은 GMM을 이용한다.
GMM 자체는 정규분포 혼합 형태의 확률분포로 데이터를 생성하는 메커니즘을 표현한 모델이다. GMM을 설명하기 위하여 먼저 클러스터 개수 $K$가 정해졌다고 하자. 데이터 $X_i, i=1, \ldots, n$은 $p$ 차원 벡터라 할때 GMM은 이러한 데이터들이 다음의 정규분포 혼합형태의 확률분포로부터 생성되었다고 가정하는 것이다.
$$P(X_i) = \sum_{k=1}^Kw_kN(X_i | \mu_k, \Sigma_k)\tag{1.1}$$
이때 $N(X_i | \mu_k, \Sigma_k)$은 평균 벡터가 $\mu_k$, 공분산 행렬이 $\Sigma_k$인 $p$ 차원 정규분포이고 $\sum_{k=1}^Kw_k=1, w_k\geq 0, k=1, \ldots, K$이다.
GMM 클러스터링은 데이터의 생성 확률 모형을 GMM이라는 가정을 사용한다.
c. GMM 클러스터링을 데이터가 속하는 클러스터를 확률적으로 할당한다.
Soft Clustering은 데이터 포인트들이 속하는 클러스터를 확률적으로 표현하는 것을 말한다(물론 실제로 클러스터에 할당할 때에는 확률이 높은 클러스터에 할당하므로 이때에는 Hard Clustering 성격을 띤다). 그렇다면 GMM은 데이터 포인트들을 어떻게 확률적으로 할당하는지 알아보자.
식 (1.1)에서 $w_k$는 클러스터 $k$를 선택할 확률 또는 클러스터 $k$에 할당할 확률이라고 볼 수 있다. 여기서는 데이터 포인트를 클러스터 $k$에 할당하는 확률이 아니라 $k$번째 확률분포(정규분포)로 선택할 확률이라고 생각하자. 이때 잠재 변수(Latent Variable) $Z_i$를 이용하여 $w_k$는 다음과 같이 표현해보자.
$$w_k = P(Z_{i}=k), \forall i = 1, \ldots, n$$
이것의 의미는 눈에는 보이지 않는(Unobservable) 잠재 변수 $Z_{i}$에 의하여 클러스터가 선택된다는 것이다.
다음으로 $Z_{i}=k$로 주어진 경우 즉 $k$번째 확률분포가 선택된 경우 데이터$X_i$의 분포는 $N(X_i|\mu_k, \Sigma_k)$이므로 이를 조건부 확률로 표현하면 다음과 같다.
$$P(X_i|Z_{i}=k) = N(X_i|\mu_k, \Sigma_k)\tag{1.2}$$
이제 우리가 알고 싶은 내용, 즉 $X_i$가 주어졌을 때 이 데이터를 클러스터 $k$에 할당할 확률 $P(Z_{i}=k|X_i)$를 알아야 한다. 이는 베이즈 정리를 이용하면 앞에서 소개한 확률로 표현할 수 있다.
$$\begin{align}P(Z_{i}=k|X_i) &= \frac{P(Z_{i}=k)P(X_i|Z_{i}=k)}{\sum_{j=1}^KP(Z_{i}=j)P(X_i|Z_{i}=j)} \\ &= \frac{P(Z_{i}=k)N(X_i|\mu_k, \Sigma_k)}{\sum_{j=1}^KP(Z_{i}=j)N(X_i|\mu_j, \Sigma_j)} \end{align}\tag{1.3}$$
GMM 클러스터링은 데이터를 식 (1.3)의 확률을 이용하여 클러스터에 할당한다.
2. Gaussian Mixture Model(가우시안 혼합 모형) 클러스터링 알고리즘
식 (1.1)를 이용하면 데이터 $X_i, i=1, \ldots, n$의 전체 로그 우도 함수는 다음과 같다는 것을 알 수 있다.
$$\begin{align}\log P(X_1, \ldots, X_n) &= \sum_{i=1}^n\log P(X_i) \\ &= \sum_{i=1}^n\log \sum_{k=1}^KP(Z_{i}=k)N(X_i | \mu_k, \Sigma_k)\\ &= \sum_{i=1}^n\log \sum_{k=1}^Kw_kN(X_i | \mu_k, \Sigma_k)\end{align}\tag{2.1}$$
GMM 클러스터링 알고리즘은 식 (2.1)을 최대화하는 방향으로 클러스터링(알고리즘)을 수행한다. 이때 $Z_k$는 실제로 관측은 되지 않지만 잠재적으로 데이터를 클러스터에 할당해주는 확률변수로 도입된 잠재 변수이다. GMM 클러스터링은 잠재 변수를 도입하여 로그 우도 함수를 최대화하는 방법 즉, EM 알고리즘을 이용하게된다. EM 알고리즘에 대한 설명은 여기를 참고하기 바란다.
$\theta = (w_1, \ldots, w_K, \mu_1, \ldots, \mu_K, \Sigma_1, \ldots, \Sigma_K)$라하고 식 (2.1)의 로그 우도함수를 $l(\theta)$라고 하자. 우리는 EM 알고리즘을 이용하여 $l(\theta)$를 최대화하는 $\theta$를 찾는 것이다.
GMM 클러스터링 알고리즘은 다음과 같다.
단계 1) 클러스터 개수 $K$, 오차 한계 $\epsilon >0$, 최대 반복수 $T$, 초기 파라미터 $\theta^{(0)}$을 설정한다.
단계 2) E-step
$t$번째 스텝과 파라미터 $\theta^{(t)}$에 대하여 $Q$ 함수를 계산한다.
$$\begin{align} Q(\theta | \theta^{(t)}) &= E_{Z|X, \theta^{(t)}} \left \{ \log f_{\theta}(Z, X) \right \} \\ &= \sum_{i=1}^nE_{Z_i|X_i, \theta^{(t)}}\left \{ \log f_{\theta} (Z_i, X_i) \right \} \\ &= \sum_{i=1}^n\sum_{k=1}^K\gamma_{k, i, \theta^{(t)}} \log P(Z_{i}, X_i | \theta) \\ &= \sum_{i=1}^n\sum_{k=1}^K\gamma_{k, i, \theta^{(t)}} \log w_kN(X_i|\mu_k, \Sigma_k) \end{align}$$
이때
$$\gamma_{k, i, \theta^{(t)}} = P(Z_{i}=k|X_i, \theta^{(t)}) = \frac{w_k^{(t)}N(X_i|\mu_k^{(t)}, \Sigma_k^{(t)})}{\sum_{j=1}^Kw_j^{(t)}N(X_i|\mu_j^{(t)}, \Sigma_j^{(t)})} $$
사실 $Q$ 함수를 계산한다는 것을 본질적으로 $\theta^{(t)}$가 주어졌을 때 $\gamma_{k, i, \theta^{(t)}}$만 정해주면 되는 것이다.
단계 3) M-step
E-step에서 유도한 $Q$함수를 최대화하는 $\theta$를 찾는다. 이게 $\theta^{(t+1)}$로 업데이트되는 것이다. 하나하나 살펴보면 다음과 같다(증명은 여기를 참고하기 바란다).
$\begin{align} & w_k^{(t+1)} = \frac{1}{n}\sum_{i=1}^n\gamma_{k, i, \theta^{(t)}} \\ & \mu_k^{(t+1)} = \sum_{i=1}^n\gamma_{k, i, \theta^{(t)}}X_i/\sum_{i=1}^n\gamma_{k, i, \theta^{(t)}} \\ & \Sigma_k^{(t+1)} = \frac{1}{\sum_{i=1}^n\gamma_{k, i, \theta^{(t)}}}\sum_{i=1}^n\gamma_{k, i, \theta^{(t)}}(X_i-\mu_k^{(t+1)})(X_i-\mu_k^{(t+1)})^t \end{align}$
단계 4) 만약 $l(\theta^{(t+1)})-l(\theta^{(t)}) < \epsilon$ 이거나 최대 반복수 $T$에 도달했으면 알고리즘을 종료하고 최종 파라미터 추정값은 $\theta^{(t+1)}$로 한다. 아니라면 $\theta^{(t)}\longleftarrow \theta^{(t+1)}$로 설정하고 단계 2)로 돌아간다.
3. Gaussian Mixture Model(가우시안 혼합 모형) 클러스터링 장단점
1) 장점
- GMM 클러스터링은 Soft Clustering이다.
기존 K-Means 클러스터링은 데이터 포인트들이 잠재 클러스터에 속하는지 안 하는지 둘 중 하나의 상태만 가능한 Hard Clustering이라면 GMM 클러스터링은 데이터 포인트들이 각 클러스터에 속할 확률을 나타낼 수 있다는 점에서 K-Means 보다 유연하다.
- 클러스터 내 데이터 분산 구조를 반영할 수 있다
GMM 클러스터링은 각 클러스터의 분산 행렬 $\Sigma_k$를 추정하고 이를 통하여 클러스터 내 분산 구조를 반영하여 좀 더 정확한 클러스터링(군집화)이 가능하다.
- 구현이 쉽다
GMM 클러스터링은 구현이 어렵지 않다.
2) 단점
- 클러스터 개수를 사전에 설정해야 한다.
GMM 클러스터링은 K-Means 클러스터링과 마찬가지로 클러스터 개수를 사전에 설정해줘야 한다. 알아서 클러스터 개수를 추정하진 않는다. 하지만 Dunn Index나 Silhouette Index를 통하여 여러 클러스터 개수에 대한 결과를 평가하여 최적 클러스터 개수를 정할 수도 있다.
- 초기값에 민감하다.
GMM 클러스터링은 초기값에 따라서 군집화 결과가 매우 달라질 수 있다.
- 파라미터 수가 많아서 데이터가 충분히 필요하다.
추정해야 할 파라미터 개수(가중치 $K$개, 평균 $p\times K$개, 분산 $\{p(p+1)/2\}\times K$개)가 굉장히 많아서 그에 따른 충분한 데이터가 모이지 않는다면 추정량의 정확성을 보장 못하고 그에 따라 클러스터링 결과의 신뢰성에도 문제가 생기게 된다.
- 범주형 데이터를 다룰 수 없다.
가우시안 분포(의 혼합 모형)를 사용하다 보니 범주형 데이터에 대하여 클러스터링은 할 수 없다. 이때에는 K-Modes라는 다른 클러스터링 알고리즘을 이용하면 가능하다고 하니 공부하고 포스팅해봐야겠다.
4. Gaussian Mixture Model(가우시안 혼합 모형) 파이썬 구현
알고리즘을 알았으니 실제로 구현을 해보자.
1) 직접 구현
먼저 샘플용 데이터를 만들어준다. 여기서는 각 클러스터마다 분산 구조(타원형 구조)를 갖도록 만들어보았다.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib
matplotlib.rcParams['axes.unicode_minus'] = False
import warnings
warnings.filterwarnings('ignore')
np.random.seed(3)
sample_size=100
x1 = 3*np.random.rand(sample_size)
x2 = np.random.rand(sample_size)+1
x3 = 2*np.random.rand(sample_size)+2
y1 = 2*x1+2+np.random.randn(sample_size)
y2 = 4*x2+5+np.random.randn(sample_size)
y3 = 0.2*x3+np.random.randn(sample_size)
y = np.array(list(y1)+list(y2)+list(y3))
x = np.array(list(x1)+list(x2)+list(x3))
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(x, y, color='k')
plt.show()
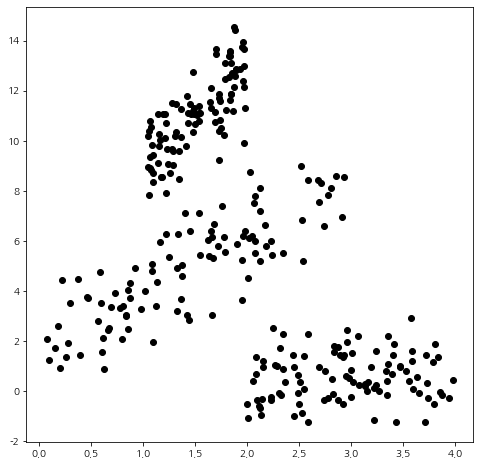
이제 주인공인 GMM 클러스터링 알고리즘을 구현한 함수(gaussian_mixture_clustering)를 나타낸 코드를 보자.
이 함수는 데이터 셋(X), 클러스터 개수(n_components), 초기 평균 벡터(init_mu), 초기 공분산 행렬(init_cov_mat), 초기 가중치(init_weights), 오차 한계(epsilon), 최대 반복수(max_iter) 그리고 결과의 재생산성을 위하여 random_state를 지정하도록 하였다.
그리고 최종 클러스터 라벨(labels), 스텝 수(iteration), 로그 우도 함수값 이력(objective_value_history)을 리턴한다.
이 함수의 구조는
초기값 설정 -> E-step 계산 -> M-step 계산
으로 이루어진다.
def gaussian_mixture_clustering(X, n_components, init_mu=None, init_cov_mat=None, init_weights=None,
epsilon=1e-4, max_iter=20, random_state=100):
from scipy.stats import multivariate_normal
import random
# set initial value
if init_mu is None:
random.seed(random_state)
idx = random.sample(range(X.shape[0]), n_components)
mu = X[idx,:]
else:
mu = init_mu
if init_cov_mat is None:
np.random.seed(random_state)
cov_list = []
for _ in range(n_components):
arr = np.random.rand(X.shape[1]**2)+0.1
temp_mat = np.triu(arr.reshape(X.shape[1], X.shape[1]))
cov_elem = temp_mat.dot(temp_mat.T)
cov_list.append(cov_elem)
cov_mat = np.array(cov_list)
else:
cov_mat = init_cov_mat
if init_weights is None:
weights = np.array([1/n_components]*n_components)
else:
weights = init_weights
objective_value = -np.infty
objective_value_history = []
iteration = 1
while(iteration<max_iter):
# E-step
assign_prob = []
for i,d in enumerate(X):
assign_prob_temp = []
for k in range(n_components):
assign_prob_temp.append(weights[k]*\
multivariate_normal(mean=mu[k],cov=cov_mat[k]).pdf(d))
assign_prob_temp = np.array(assign_prob_temp)
assign_prob_temp = assign_prob_temp/np.sum(assign_prob_temp)
assign_prob.append(assign_prob_temp)
assign_prob = np.array(assign_prob)
# M-step
temp_sum = np.sum(assign_prob, axis=0)
next_weights = []
next_mu = []
next_cov_mat = []
for k in range(n_components):
mu_numerator = np.sum(np.expand_dims(assign_prob[:,k],axis=1)*X, axis=0)
next_mu_vector = mu_numerator/temp_sum[k]
next_mu.append(next_mu_vector)
next_weights.append(temp_sum[k]/X.shape[0])
t = []
for i,d in enumerate(X):
tt = d-next_mu_vector
tt = np.expand_dims(tt,axis=1)
tt_cov = np.matmul(tt,tt.transpose())
tt_term = assign_prob[i][k]*tt_cov
t.append(tt_term)
t = np.array(t)
cov_numerator = np.sum(t,axis=0)
next_cov_mat.append(cov_numerator/temp_sum[k])
next_objective_value = 0
for x in X:
value = np.log(np.sum([next_weights[k]*multivariate_normal(mean=next_mu[k],cov=next_cov_mat[k]).pdf(x)
for k in range(n_components)]))
next_objective_value += value
objective_value_history.append(next_objective_value)
if next_objective_value-objective_value<=epsilon:
labels = [np.argmax(x) for x in assign_prob]
return (labels, iteration, objective_value_history)
else:
weights = next_weights
mu = next_mu
cov_mat = next_cov_mat
objective_value = next_objective_value
iteration += 1
labels = [np.argmax(x) for x in assign_prob]
return (labels, iteration, objective_value_history)
이제 GMM 클러스터링이 잘 작동하는지 확인해볼 시간이다. 먼저 분산 구조를 잘 반영하지 못하는 K-Means 클러스터링의 약점을 눈으로 확인해보자. KMeans의 사용법은 여기를 참고하자.
from sklearn.cluster import KMeans
init_centers = np.array([[1.5,4], [3.5,0], [1.5, 11]]) # 초기 중심값
kmeans = KMeans(n_clusters=3, init=init_centers, random_state=100)
kmeans.fit(X) # 클러스터링 수행
labels = kmeans.labels_ # 최종 클러스터 라벨
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(X[:,0], X[:,1], c=labels)
plt.show()
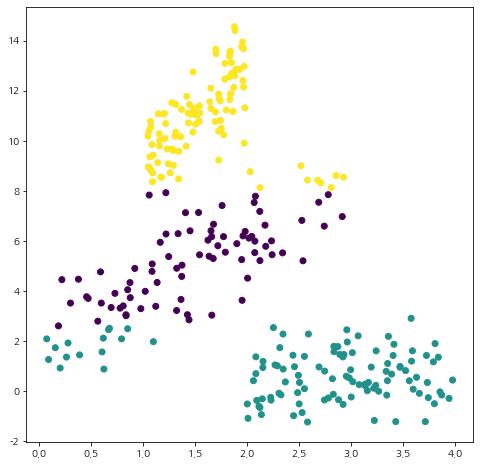
이제 GMM 클러스터링을 해보자.
n_components = 3
init_mu = np.array([[1.5,4], [3.5,0], [1.5, 11]])
epsilon=1e-4
max_iter=20
random_state=100
labels, _, _ = gaussian_mixture_clustering(X, n_components, init_mu=init_mu, init_cov_mat=None, init_weights=None,
epsilon=1e-4, max_iter=20, random_state=100)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(X[:,0], X[:,1], c=labels)
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()
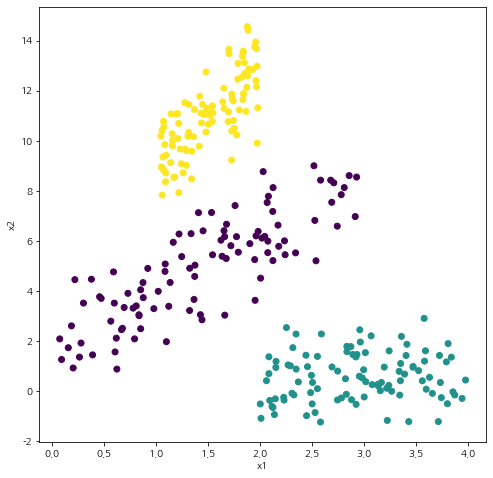
시각화 결과에서 알 수 있듯이 GMM 클러스터링은 군집 내 분산 구조를 반영하여 군집화가 이루어지는 것을 알 수 있다.
2) Scikit-Learn 모듈 사용
GMM 클러스터링은 Scikit-Learn 모듈에서 GaussianMixture을 이용해서 구현할 수도 있다.
먼저 GaussianMixture 클래스에 초기 인자로 클러스터 개수(n_components)를 설정한다. 나는 means_init에 초기 평균 벡터를 설정해주었다.
그리고 fit을 통해 GMM 클러스터링을 수행하고 predict를 통해 최종 클러스터 라벨을 얻는다. fit이나 predict에는 사용된 데이터 셋(X)을 넣어준다. 자세한 설명은 Scikit-Learn 문서를 참고하기 바란다.
from sklearn.mixture import GaussianMixture
init_centers = np.array([[1.5,4], [3.5,0], [1.5, 11]]) # 초기 평균값
# 클러스터 개수 3개, means_init으로 초기 평균 벡터 설정, 결과 재생산성을 위해 random_state 설정
gmm = GaussianMixture(n_components=3, means_init=init_centers, random_state=100)
gmm.fit(X) # GMM 클러스터링 수행
labels = gmm.predict(X) # 최종 클러스터 라벨링
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.scatter(X[:,0], X[:,1], c=labels)
plt.show()
위 코드를 수행하면 직접 구현한 함수와 동일한 결과를 얻을 수 있다.
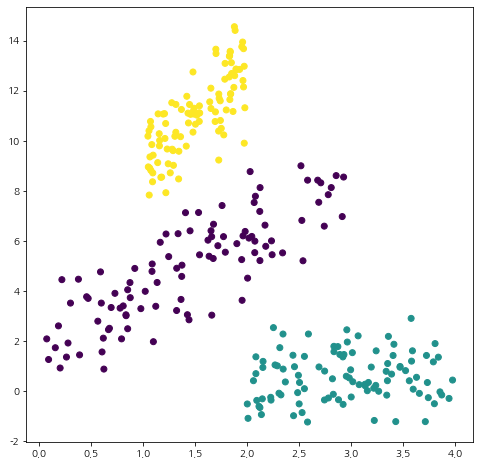
확실한 건 직접 구현한 것보다 Scikit-Learn을 이용하는 것이 속도가 훨씬 빨랐다. ㄷㄷ;;
Scikit-Learn 쓰자!!
이번 포스팅에서는 Gaussian Mixture Model을 이용한 클러스터링에 대해서 알아보았다. 직접 구현도 해보고 EM 알고리즘도 다시 복습할 수 있었던 좋은 시간이었다.
참고자료
Gaussian mixture models - https://mbernste.github.io/posts/gmm_em/
문일철 - 인공지능 및 기계학습 개론 2
'통계 > 머신러닝' 카테고리의 다른 글
| 14. 클러스터링(군집화) 평가지표 Silhouette(실루엣) 지수(계수)에 대해서 알아보자 with Python (410) | 2022.05.01 |
|---|---|
| 13. Box-Cox Transformation(변환)에 대해서 알아보자 with Python (385) | 2022.05.01 |
| 12. 클러스터링(군집화) 평가 지표 Dunn Index with Python (401) | 2022.04.22 |
| 11. K-Means 클러스터링(Clustering, 군집화)에 대해서 알아보자 with Python (408) | 2022.04.21 |
| 10. 가지치기(Pruning)에 대해서 알아보자 with Python (1267) | 2021.07.05 |
댓글