이번 포스팅에서는 나이브 베이즈 분류기(Naive Bayes Classifier : NBC)에 대해서 알아보려고 한다. 먼저 나이브 베이즈 분류기를 알아보기 전에 베이즈 분류기에 대해서 알면 좋다. 왜냐하면 베이즈 분류기랑 나이브 베이즈 분류기랑 헷갈릴 수 있기 때문이다. 베이즈 분류기에 대해서는 이전 포스팅에서 다루었으니 한번 보고 오면 좋다.
여기서 다루는 내용은 다음과 같다.
1. 나이브 베이즈 분류기
- 정의 -
이전 포스팅에서 베이즈 분류기는 0-1 손실 함수의 기대값을 최소화시키는 분류기라고 하였다. 또한 독립변수 X, 출력 변수 y(∈{1,2,…,J})에 대하여 베이즈 분류기를 fBayes라 하면
fBayes(X)=argmax
임을 보였다.
여기서 베이즈 법칙에 의하면 X 가 주어졌을 때 y 의 조건부 확률은 다음과 같이 쓸 수 있다.
\begin{align}P(y=j|X) &= \frac{P(y=j)P(X | y = j)}{P(X)} \\ &\propto P(y=j)P(X | y=j ) \end{align}
여기서 마지막 비례 표시는 y와 상관없는 부분에 대하여 비례한다는 뜻이다.
위 식이 의미하는 바는 P(y=j|X)를 최대화하는 것은 P(y=j)P(X | y=j)를 최대화하는 것과 똑같다는 것이다. 따라서 베이즈 분류기 (1)은 다음과 같이 다시 쓸 수 있다.
\DeclareMathOperator*{\argmaxB}{argmax} f^{\text{Bayes}}(X)=\argmaxB_{j \in \{1,2,\ldots,J\}} \underbrace{P(y=j)P(X|y=j)}_{(3)}\tag{2}
이제 나이브 베이즈 분류기를 정의할 수 있는 초석은 깔아놓았다. 먼저 X=(X_1, X_2, \ldots, X_p)^t 라 하자. 이때 다음과 같이 조건부 독립을 가정한다(이러한 가정을 Naive Bayes Assumption 이라고도 한다).
조건)
P(X|y=j) = P(X_1, X_2, \ldots, X_p|y=j) = \prod_{l=1}^pP(X_l|y=j)
이러한 조건하에서 다음과 같은 분류기 f^{\text{Naive}}를 생각할 수 있다.
\DeclareMathOperator*{\argmaxB}{argmax} f^{\text{Naive}}(X) = \argmaxB_{j\in\{1,2,\ldots,J\}}P(y=j)\prod_{l=1}^pP(X_l|y=j)\tag{*}
이때 f^{\text{Naive}}를 나이브 베이즈 분류기라 한다. 간단히 말하면 클래스가 주어졌을 때 독립변수의 조건부 확률에 조건부 독립 가정을 추가한 베이즈 분류기가 나이브 베이즈 분류기인 것이다. 나이브 베이즈 분류기를 정의하기 위해서 서론이 너무 길었다.
- 추정 방법 -
나이브 베이즈 분류기를 구하기 위해서는 y의 Marginal 분포 P(y = j)와 특정 범주가 주어졌을 때 독립변수의 조건부 확률 분포 P(X_l | y=j)을 알아야 한다. 하지만 대부분의 경우 이를 알 수가 없다. 따라서 데이터를 이용하여 각 확률을 추정해야 한다.
나이브 베이즈 분류기 추정방법은 독립변수의 유형에 따라 달라진다.
1) 독립변수가 범주형인 경우
2) 독립변수가 연속형인 경우
3) 독립변수가 2개 이상의 특정 카테고리에 대한 빈도수(count)인 경우
이제 각각의 경우에 대하여 추정 방법을 알아보자. 먼저 설명의 편의를 위해 독립변수가 한 개인 경우만 살펴보자(여러 개인 경우는 한 개씩 추정하여 곱하면 되는데 아래에서 설명한다).
1) 독립변수가 범주형인 경우
먼저 독립변수가 K개의 범주를 갖는다고 하자. 즉, X_i\in\{1, 2, \ldots, K\}이다.
나이브 베이즈 분류기를 추정하기 위해 먼저 n개의 데이터 (X_i, y_i), \;\;i=1,\ldots,n가 있는 상황에서 식 (2)의 (3) 부분을 추정해야 한다.
먼저 P(y=j)은 전체 데이터 중에서 출력 변수의 범주 j에 해당하는 데이터의 비율로 추정한다.
\hat{P}(y=j) = \frac{1}{n}\sum_{i=1}^nI(y_i=j), \;\;j=1, 2, \ldots,J
(J는 출력 변수의 범주이고 K는 독립변수의 범주라는 것을 잊지 말자!)
마찬가지로 \hat{P}(X=k|y=j)는 출력 변수의 범주가 j인 데이터 중에서 독립변수의 범주가 k인 데이터의 비율로 추정한다.
\hat{P}(X=k|y=j) = \frac{\sum_{i=1}^nI(X_i=k, y_i=j)}{\sum_{i=1}^nI(y_i=j)}, \;j=1,\ldots,J, \; k=1,\ldots,K\tag{4}
따라서 범주형 독립변수 X =k가 있을 때(X는 학습 데이터 셋에 포함될 수도 있고 안될 수도 있다) 나이브 베이즈 분류기는 다음과 같이 추정할 수 있다.
\DeclareMathOperator*{\argmaxB}{argmax} \begin{align}\hat{f}^{\text{Naive}}(X=k) &= \argmaxB_{j\in\{1,2,\ldots,J\}} \hat{P}(y=j) \hat{P}(X=k|y=j) \\ &= \argmaxB_{j\in\{1,2,\ldots,J\}}\left[\frac{1}{n}\sum_{i=1}^nI(y_i=j)\right]\left[ \frac{\sum_{i=1}^nI(X_i=k, y_i=j)}{\sum_{i=1}^nI(y_i=j)}\right]\end{align}
독립변수 범주 개수가 2인 경우의 나이브 베이즈 분류기를 베르누이 나이브 베이즈 분류기(Bernoulli Naive Bayes Classifier)라고 한다.
- Additive Smoothing -
(4) 식에서 오른쪽 부분을 살펴보자. 보면 만약 X_i=k, (i=1,\ldots,n)인 경우가 학습 데이터에 없다면 \sum_{i=1}^nI(X_i=k, y_i=j)=0 이 되므로 새로운 범주형 독립변수 X=k에 대하여 \hat{f}^{\text{Naive}}(X=k)=0 이 되어 예측을 할 수 없게된다. 이는 학습 데이터에 존재하지 않으니 새로운 데이터가 들어와도 없을 것이라고 학습된 것이며 다시 말하면 학습 데이터에 과적합(Overfitting)된 결과인 것이다. 이런 상황은 메일에 포함된 단어를 이용하여 스팸메일인지 정상메일인지 예측하는 문제에서 많이 발생된다. 새로운 데이터에는 포함된 단어가 학습 데이터에 존재하지 않을 수 있기 때문이다.
따라서 (4) 식의 오른쪽에서 P(X=k|y=j)의 추정값이 0이 되는 것을 방지하기 위하여 매개변수 l\geq 0을 도입한다.
\hat{P}^{l-\text{smoothed}}(X=k|y=j) = \frac{\sum_{i=1}^nI(X_i=k, y_i=j) + l}{\sum_{i=1}^nI(y_i=j) + l\cdot K}, \tag{5} \\ \;j=1,\ldots,J, \; k=1,\ldots,K
이렇게 l을 도입하여 (4)의 오른쪽 부분을 수정하는 기법을 Additive Smoothing이라 하며 l=1인 경우 (5)를 특별히 Laplace Smoothing이라 한다.
Additive Smoothing을 이용한 나이브 베이즈 분류기는 다음과 같다.
\DeclareMathOperator*{\argmaxB}{argmax} \begin{align}\hat{f}^{\text{Naive}}(X=k) &= \argmaxB_{j\in\{1,2,\ldots,J\}} \hat{P}(y=j) \hat{P}^{l-\text{smoothed}}(X=k|y=j) \\ &= \argmaxB_{j\in\{1,2,\ldots,J\}}\left[\frac{1}{n}\sum_{i=1}^nI(y_i=j)\right]\left[ \frac{\sum_{i=1}^nI(X_i=k, y_i=j)+l}{\sum_{i=1}^nI(y_i=j)+l\cdot K}\right]\end{align}
- l의 해석 -
\alpha = \sum_{i=1}^nI(y_i=j)/(\sum_{i=1}^nI(y_i=j)+l\cdot K)라고 하면 0 \leq \alpha \leq 1이고 (5)의 오른쪽은 다음과 같아짐을 알 수 있다.
\alpha\frac{\sum_{i=1}^nI(X_i=k, y_i=j)}{\sum_{i=1}^nI(y_i=j)} + (1-\alpha)\frac{1}{K}
베이지안 관점에서 l을 y=j이 주어진 상황에서, X=k인 prior 샘플 수라고 해석한다.
먼저 l=0 인 경우는 \alpha=1 이 되어 (5)는 (4)와 같아지며 이는 사전 정보를 전혀 사용하지 않은(prior 샘플이 하나도 없는) 오로지 관측된 데이터만을 사용한 추정량이라고 볼 수 있다. l \rightarrow \infty일 때 \alpha \rightarrow 0이 되고 (5)의 오른쪽 부분은 1/K로 수렴하게 된다. 관측된 데이터가 적을 경우(l이 크다는 것은 prior 샘플이 많다는 뜻이며 이는 반대로 관측된 데이터의 비율이 작다고 볼 수 있다) P(X=k|y=j)의 값을 1/K으로 추정한다고 볼 수 있으며 이는 "관측하지 못한 사건에 대해서 가장 공평한 확률(독립변수가 총 K개 범주를 갖고 있으므로 j가 주어졌을 때 독립변수가 k인 조건부 확률을 모두 동일하다고 판단하는 것)을 적용하는 것이 좋다"는 사전 정보를 이용했다고 해석할 수 있다.
- l의 선택 -
기본적으로 l은 교차검증(Cross-validation)을 이용하여 선택한다. 또한 위키 백과에 따르면 l=1을 사용해야 한다는 주장이 있다. 또한 독립변수가 가질 수 있는 모든 범주를 알고 학습 데이터의 모든 범주가 나왔다면 l=0으로 쓰는 것도 고려해보자.
2) 독립변수가 연속형인 경우
독립변수 X가 연속형인 경우 y=j가 주어졌을 때 X의 분포를 정규분포로 가정하여 나이브 베이즈 분류기를 추정한다.
X | y=j \sim N(\mu_j, \sigma_j^2)
우리는 데이터 (X_i, y_i), \;\;i=1,\ldots,n 로부터 \mu_j, \sigma_j^2을 추정해야 한다.
먼저 \mu_j는 출력 변수의 클래스가 j인 데이터에 포함된 독립변수 X_i의 평균으로 추정한다.
\hat{\mu}_j=\frac{\sum_{i=1}^nI(y_i=j)X_i}{\sum_{i=1}^nI(y_i=j)}
다음으로 \sigma^2_j은 출력 변수의 클래스가 j인 데이터에 포함된 독립변수 X_i의 분산으로 추정한다.
\hat{\sigma_j}^2 = \frac{\sum_{i=1}^nI(y_i=j)(X_i-\hat{\mu}_j)^2}{\sum_{i=1}^nI(y_i=j)}
이를 이용하여 나이브 베이즈 분류기를 다음과 같이 추정한다.
\DeclareMathOperator*{\argmaxB}{argmax} \begin{align}\hat{f}^{\text{Naive}}(X) &= \argmaxB_{j\in\{1,2,\ldots,J\}} \hat{P}(y=j) f(X|\hat{\mu_j},\hat{\sigma}_j^2) \\ &= \argmaxB_{j\in\{1,2,\ldots,J\}}\left[\frac{1}{n}\sum_{i=1}^nI(y_i=j)\right]\left[ \frac{1}{\sqrt{2\pi\hat{\sigma}_j^2}} \exp\left(-\frac{(X-\hat{\mu}_j)^2}{2\hat{\sigma}_j^2}\right) \right]\end{align}
정규 분포(가우시안 분포)를 이용하여 나이브 베이즈 분류기를 구했으므로 이를 가우시안 나이브 베이즈 분류기(Gaussian Naive Bayes Classifier)라고 한다.
- 독립변수가 범주형인 경우와 비교 -
독립변수가 범주형인 경우의 나이브 베이즈 분류기는 조건부 확률 P(X=k|y=j)를 추정했지만 연속형인 경우에는 조건부 확률 밀도 함수 f(X|\mu_j, \sigma^2_j)를 추정했다는 차이가 있다. 확률 밀도 함수는 확률과 다르게 1보다 큰 값을 가질 수 있다. 따라서 모형을 구현할 때 1보다 큰 값이 나왔다고 당황할 필요가 없다.
- 조건부 확률 밀도 함수의 추정 -
여기서는 정규분포를 가정하여 조건부 확률 밀도 함수를 추정했지만 커널 밀도 함수 추정(Kernel density estimation) 방법을 이용할 수도 있다. 커널 밀도 함수 추정은 추후에 포스팅하겠다.
3) 독립변수가 2개 이상의 특정 카테고리에 대한 빈도수(count)인 경우
독립변수가 2개 이상의 특정 카테고리에 대한 빈도수인 경우가 있다. 예를 들면 주어진 문서에 여러 단어가 등장할 테고 특정 단어가 나타난 횟수를 독립변수로 둘 수 있다. 여기서는 문서와 단어를 이용하여 설명하려고 한다. 그리고 문서의 카테고리(j=1, \ldots, J)를 예측하는 것이 목표라고 해보자. 먼저 학습 데이터에 있는 중복되지 않는 모든 단어의 개수를 D라 하자(서로 다른 단어가 D개 있는 것이다). X_d, d=1, \ldots, D를 d 번째 단어가 나온 횟수라고 하면 y=j일 때 \tilde{X}=(X_1, X_2, \ldots, X_D)의 조건부 확률 분포를 다항 분포로 볼 수있다.
P(\tilde{X}|y=j) = \frac{m!}{X_1!\cdot X_2!\cdots X_D!}\prod_{d=1}^Dp_{dj}^{X_d}\tag{6}
여기서 m = \sum_{d=1}^DX_d 로 주어진 문서 내 전체 단어의 개수이며, p_{dj}는 문서 카테고리가 j인 경우에 d 번째 단어가 선택될 확률이며 \sum_{d=1}^Dp_{dj} = 1, \forall j이다.
(6)을 구하기 위해서 p_{dj}를 알아야 하는데 이 값을 모르기 때문에 데이터를 이용하여 추정해야 한다.
y_i를 i 번째 문서의 카테고리, 즉, y_i\in \{1, \ldots, J\} 라하자. 그리고 i 번째 문서에서 d 번째 단어가 나온 횟수를 X_{id} 그리고 \tilde{X}_i = (X_{i1}, X_{i2}, \ldots, X_{iD})^t라고 하자. 이때 p_{dj}는 다음과 같이 추정한다.
\hat{p}_{dj} = \frac{\sum_{i=1}^nI(y_i=j)X_{id}+l}{\sum_{i=1}^n\sum_{k=1}^DI(y_i=j)X_{ik}+l\cdot D}, \;\;l\geq 0
매개변수 l의 값은1) 독립변수가 범주형인 경우에서 언급한 방법으로 선택한다.
나이브 베이즈 분류기는 다음과 같이 추정할 수 있다.
\DeclareMathOperator*{\argmaxB}{argmax} \begin{align}\hat{f}^{\text{Naive}}(\tilde{X}) &= \argmaxB_{j\in\{1,2,\ldots,J\}} \hat{P}(y=j) P(\tilde{X}|y=j) \\ &= \argmaxB_{j\in\{1,2,\ldots,J\}}\left[\frac{1}{n}\sum_{i=1}^nI(y_i=j)\right]\left[ \frac{m!}{X_{1}!\cdot X_{2}!\cdots X_{D}!}\prod_{d=1}^D\hat{p}_{dj}^{X_{d}} \right] \\ &= \argmaxB_{j\in\{1,2,\ldots,J\}}\left[\frac{1}{n}\sum_{i=1}^nI(y_i=j)\right]\left[ \prod_{d=1}^D\hat{p}_{dj}^{X_{d}} \right] \end{align}
세 번째 등식은 j와 상관없는 양수는 제거를 해도 최대값을 구하는 데 영향이 없기 때문에 성립한다.
다항 분포를 이용하여 나이브 베이즈 분류기를 구했으므로 이를 다항 나이브 베이즈 분류기(Multinomial Naive Bayes Classifier)라고 한다.
- 단어의 집합 크기에 대하여 -
여러 자료를 찾아봐도 D라는 친구가 학습 데이터에 속한 전체 단어 개수라고 한다. 즉, Additive Smoothing에서는 새로운 값이 들어왔을 때 조건부 확률 값을 1/D로 추정하겠다는 말인데 이 부분이 좀 골치가 아팠다. 왜냐하면 학습 데이터에는 없는 단어가 테스트 데이터에는 있을 수 있기 때문이다. 그래서 1/D라는 확률의 의미가 이상해지는 것이다. 내 생각에는 예측 단계에서 이전에 없던 단어가 나올 때마다 하나씩 더해주어 D를 업데이트해야 한다고 생각하는 데 이에 대한 부분을 찾지 못했다. 다른 자료에는 예측단계에서 업데이트하지 않고 그냥 1/D 썼다. 지금까지 호기심 많은 나의 생각이었다.
- 독립변수가 여러개인 경우 -
지금까지는 독립변수가 하나인 경우(독립변수가 특정 단어에 대한 빈도수인 경우는 (단어, 단어 빈도수)의 쌍으로 볼 수 있어서 이 때는 독립변수가 2개라고 생각할 수 있지만 순서를 이용하면 하나라고 볼 수 있다)를 살펴보았는데 이로부터 독립변수가 여러 개인 경우의 나이브 베이즈 분류기로 쉽게 확장할 수 있다.
일반적인 경우를 다루기 위하여 독립변수 X에는 범주형, 연속형, 그리고 빈도수를 모두 포함한다고 하자. 먼저 범주형 독립변수는 G 개, 연속형은 C개, 그리고 특정 카테고리와 해당 카테고리의 빈도수로 이루어진 독립변수는 M개 있다고 하자.
여기서 잠깐!!
독립변수의 종류가 3가지 모두 포함된 경우 데이터 구조를 이해하기가 생각보다 쉽지 않고 또한 수식으로 정교하게 풀어쓰는데 많은 노력이 든다. 그래서 보통 나이브 베이즈 분류기를 설명할 때 독립변수가 하나인 경우만을 다룬다.
데이터 구조를 이해하기가 쉽지 않은 이유는 범주형, 연속형은 하나의 행에 데이터 하나가 들어가지만 3번째 경우는 좀 다르기 때문이다. 억지로 만든 예를 한번 살펴보자.
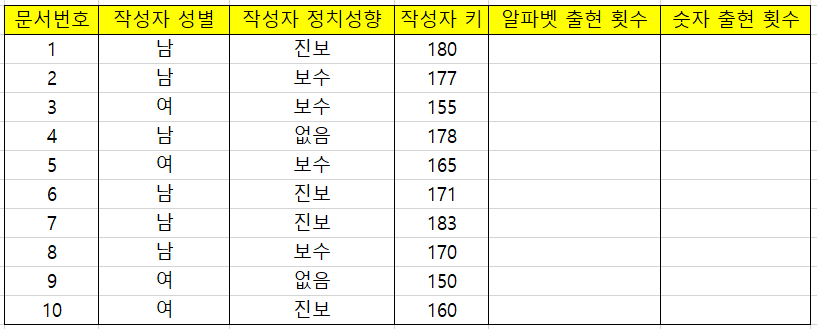
데이터의 개수는 10개이며 범주형 독립변수는 작성자 성별, 작성자 정치성향 2개이다(G=2). 그리고 연속형 변수는 작성자 키 하나 있다(C=1). 반면 특정 카테고리에 대한 빈도수를 나타내는 독립변수는 알파벳 출현 횟수와 숫자 출현 횟수로 2개가 있다(M=2). 범주형 변수나 연속형 변수는 하나의 행에 하나씩 들어가지만 알파벳 출현 횟수와 숫자 출현 횟수는 하나의 행에 어떻게 넣어야 할지 고민이 된다. 여기서는 아래와 같이 하나의 행에 배열 형태로 들어간다고 하겠다.
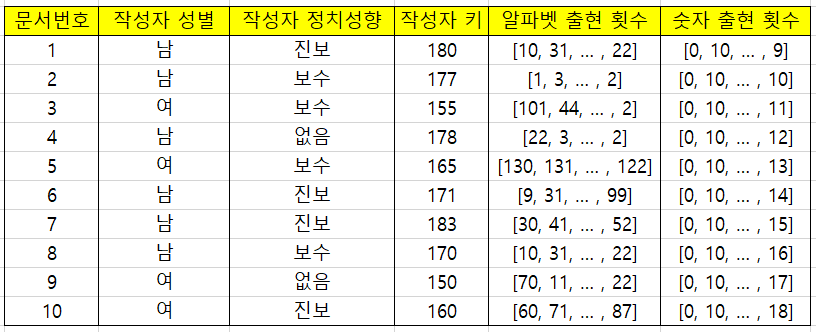
알파벳 출현 횟수에서 각행의 배열 크기는 26(알파벳 종류)이며 배열의 순서는 알파벳 순서와 같다. 숫자 출현 횟수에서 각행의 배열 크기는 10(0~9)이며 배열의 순서는 0부터 9까지이다.
"지금 이 얘기를 왜 했나?" 할 수 있지만 독립변수의 종류가 앞서 언급한 3개가 동시에 있는 경우에는 데이터 구조가 머릿속으로 잘 그려지지 않을 수 있으므로 이해를 돕고자 설명한 것이다.
X^{\text{C}}은 범주형 독립변수들의 집합이며 X^{\text{C}} = (X^{\text{C}}_1, \ldots, X^{\text{C}}_G) 이고 X^{\text{Con}}은 연속형 독립변수들의 집합이며 X^{\text{Con}} = (X^{\text{Con}}_1, \ldots, X^{\text{Con}}_C) 이다. 마지막으로 \tilde{X}^{\text{N}} 특정 카테고리에 대한 빈도수를 나타내는 독립변수들의 집합이다. \tilde{X}^{\text{N}}=(\tilde{X}^{\text{N}}_1, \ldots, \tilde{X}^{\text{N}}_M).
종합하면 독립변수의 총집합은 X = (X^{\text{C}}, X^{\text{Con}}, \tilde{X}^{\text{N}}) 이다.
이제 학습 데이터 (X_i, y_i)에 대해서 나이브 베이즈 분류기를 구해보자. (*) 식에서 P(y=j)는 앞서 살펴본 것과 동일하게 추정한다.
\hat{P}(y=j) = \frac{1}{n}\sum_{i=1}^nI(y=j), \;\;j=1, 2, \ldots, J
이제 y=j 일때 개별 독립변수 X_l(\in X,\; l=1, 2, \ldots, G+C+M) 의 조건부 확률을 추정해야 한다. 조건부 독립이기 때문에 어떤 순서로 계산하든 상관없으므로 독립변수의 종류끼리 묶어서 각 종류별로 추정하고자 한다.
case 1 X^{\text{C}}
\hat{P}(X^{\text{C}} | y=j) = \prod_{g=1}^G\hat{P}(X_{g}=k_g|y=j)
여기서
\hat{P}(X_{g}=k_g|y=j) = \left[ \frac{\sum_{i=1}^nI(X_{ig}=k_g, y_i=j)}{\sum_{i=1}^nI(y_i=j)}\right] .
case 2 X^{\text{Con}}
\hat{P}(X^{\text{Con}} | y=j) = \prod_{c=1}^Cf(X_{c}|\hat{\mu}_{jc}, \hat{\sigma}_{jc}^2)
여기서
f(X|\hat{\mu}_{jc}, \hat{\sigma}_{jc}^2) = \frac{1}{\sqrt{2\pi\hat{\sigma}_{jc}^2}} \exp\left(-\frac{(X-\hat{\mu}_{jc})^2}{2\hat{\sigma}_{jc}^2}\right)
이고
\begin{align}\hat{\mu}_{jc}&=\frac{\sum_{i=1}^nI(y_i=j)X_{ic}}{\sum_{i=1}^nI(y_i=j)} \\ \\ \hat{\sigma}_{jc}^2 &= \frac{\sum_{i=1}^nI(y_i=j)(X_{ic}-\hat{\mu}_j)^2}{\sum_{i=1}^nI(y_i=j)} \end{align}
case 3 \tilde{X}^{\text{N}}
\hat{P}( \tilde{X}^{\text{N}} | y=j) = \prod_{m=1}^MP(\tilde{X}^{\text{N}}_m|y=j)
여기서
P(\tilde{X}^{\text{N}}_m|y=j) = \frac{N_m!}{X_{m1}!\cdot X_{m2}!\cdots X_{mD_m}!} \prod_{d=1}^{D_m}\hat{p}_{mdj}^{X_{md}}
이고
\hat{p}_{mdj} = \frac{\sum_{i=1}^nI(y_i=j)X_{imd}+l}{\sum_{i=1}^n\sum_{k=1}^DI(y_i=j)X_{imk}+l\cdot D_m}, \;\;l\geq 0,
\tilde{X}^{\text{N}}_m = (X_{m1}, \ldots, X_{mD_m}), \;\;N_m = \sum_{d=1}^{D_m}X_{md} 이다.
독립변수 X에 대하여 나이브 베이즈 분류기는 다음과 같다.
\DeclareMathOperator*{\argmaxB}{argmax} \hat{f}^{\text{Naive}}(X) = \argmaxB_{j\in\{1,2,\ldots,J\}} \underbrace{\left\{\hat{P}(y=j) \hat{P}(X^{\text{C}} | y=j) \hat{P}(X^{\text{Con}} | y=j) \hat{P}( \tilde{X}^{\text{N}} | y=j)\right\}}_{(8)}\tag{7}
그런데 식 (7)을 보면 확률의 곱셈이 많이 들어간다(4개 밖에 없는 것 같지만 첫 번째 항을 뺀 나머지는 수많은 곱셈을 포함할 수 있다). 잘 알다시피 확률은 0과 1 사이의 값이고 각 확률이 매우 작은 값이라면 곱셈을 하는 데 있어서 컴퓨터가 제대로 계산할 수 없는 상황이 발생한다(Underflow). 따라서 이를 완화하기 위하여 다음과 같이 Log 함수를 이용하여 나이브 베이즈 분류기를 추정할 수 있다.
\DeclareMathOperator*{\argmaxB}{argmax} {\scriptstyle \hat{f}^{\text{Naive}}(X) = \argmaxB_{j\in\{1,2,\ldots,J\}} \underbrace{\left\{\log(\hat{P}(y=j)) + \log(\hat{P}(X^{\text{C}} | y=j)) + \log(\hat{P}(X^{\text{Con}} | y=j)) + \log(\hat{P}( \tilde{X}^{\text{N}} | y=j))\right\}}_{(10)}\tag{9}}
왜냐하면 Log 함수는 증가(Strict increasing)함수이기 때문에 식 (7)의 (8)을 최대화하는 문제와 식 (9)의 (10)을 최대화하는 문제가 같아지기 때문이다.
요약하면 다음과 같다.
1) 출력 변수의 라벨 확률 $P(y=j)$을 추정한다.
2) 개별 독립변수 X의 조건부 확률 P(X|y=j)를 독립변수의 유형에 따라 추정한다.
3) 1), 2)에서 구한 값을 모두 곱하고(또는 log를 이용하여 합산) 이 값을 최대화하는 라벨을 예측값으로 출력한다.
2. 실제 데이터 적용
먼저 이번 포스팅에서 사용할 데이터를 다운받아보자.
필요한 모듈을 임포트 해보자.
import pandas as pd import numpy as np import random import re import warnings warnings.filterwarnings('ignore') from collections import defaultdict from tqdm import tqdm from scipy.stats import norm from sklearn.model_selection import train_test_split from sklearn.naive_bayes import GaussianNB from sklearn.naive_bayes import MultinomialNB from sklearn.feature_extraction.text import CountVectorizer
1. 출력 변수가 2개 클래스인 경우
먼저 Adult Data Set을 이용하여 나이브 베이즈 분류기를 구현해보자. 데이터를 불러온다.
## http://archive.ics.uci.edu/ml/datasets/Adult df = pd.read_csv('adult.csv')
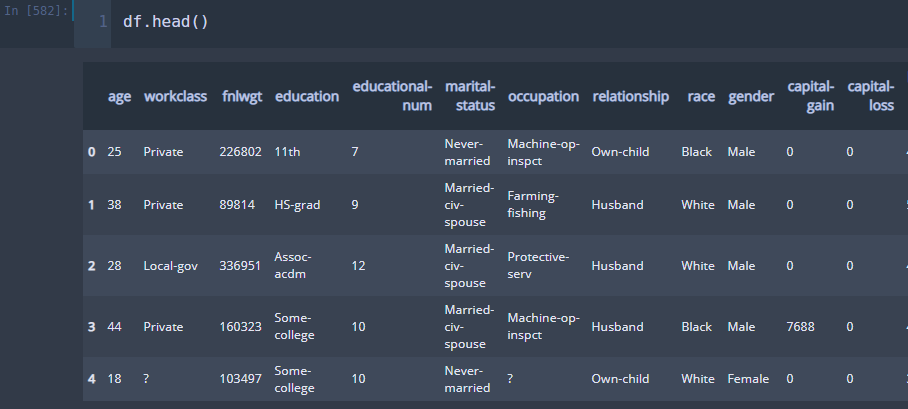
나이브 베이즈 분류기를 구현하기에 앞서 간단한 데이터 전처리를 해준다. 이 데이터에는 결측치를 '?'로 표시해두었다. 따라서 이를 NaN로 바꾼 뒤 제거해준다.
for col in df.columns: df[col].replace('?',np.NaN,inplace=True) ## ?를 NaN을 바꾼다. df.dropna(inplace=True) ## NaN 제거
결측치가 있는지 없는지 확인해보겠다. 아래와 같이 info를 이용하면 결측치가 있는지 없는지 알 수 있다. 이에 대한 설명은 여기를 참고하기 바란다.
df.info()
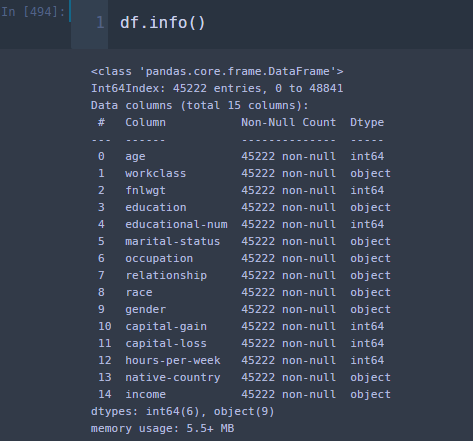
그리고 범주형 변수에 대해서 각 범주를 숫자로 변환해주자. 이를 위한 함수를 하나 만들었다. 이 함수는 범주형 칼럼에 대하여 범주를 숫자로 변환한 뒤 열 크기에 맞게 리스트로 출력한다. 나는 추가로 res_dict를 리턴하도록 했는데 이는 숫자를 다시 원래 범주로 바꾸기 위한 것이다. 필요할 줄 알았는데 전혀 필요 없었다 ㅠ.ㅠ
def convert_label(df, column): unique_value = df[column].unique() res = [] res_dict = dict() for i, u in enumerate(unique_value): res_dict[i] = u for v in df[column]: idx = np.where(unique_value==v)[0][0] res.append(idx) return res, res_dict
이제 데이터에서 어떤 칼럼이 범주형인지 리스트로 선언하고 범주를 숫자로 바꿔준다.
## category to num categorical_column = ['workclass','education','marital-status',\ 'occupation','relationship','race','gender','native-country'] res_dicts = dict() for col in categorical_column+['income']: res, res_dict = convert_label(df,col) res_dicts[col] = res_dict df[col] = res
데이터 전처리는 끝났다. 나이브 베이즈 분류기를 구현해보자. 먼저 확률 계산에 필요한 함수를 만들어 준다. 다음은 P(y=j)의 추정값을 구하는 함수이다. 출력 변수(target)의 각 라벨(label)에 대하여 P(y=j)의 추정값을 구해준다.
def estimate_target_prob(df, target, label): return len(df[df[target]==label])/len(df)
다음은 독립변수가 범주형인 경우에 확률값(식 (5)의 오른쪽 )을 추정하는 함수다. 각 독립변수(column)가 가질 수 있는 범주(category)와 출력 변수(target)의 라벨(label)에 대하여 값을 계산한다.
def category_prob(df, column, category, target, label, l=1): numerator = len(df[(df[column]==category)&(df[target]==label)]) + l denominator = len(df[df[target]==label])+l*len(df[column].unique()) return numerator/denominator
다음은 독립변수가 연속형일 때 평균과 표준편차의 추정치를 계산하는 함수이다.
def estimate_mean_std(df, column, target, label): temp = df[df[target]==label] mu = temp[column].mean() std = temp[column].std() return mu, std
다음은 나이브 베이즈 분류기 클래스이다.
class NaiveBaysClassifier: def __init__(self,unique_label,target,categorical_column=[]): self.__reference_dict = None self.__prior_probs = None self.__categorical_column = categorical_column self.__unique_label = unique_label self.__target = target def train(self, train_df): reference_dict = dict() for col in train_df.columns[:-1]: ## target column은 마지막열에 있다고 가정. temp_res = [] for label in self.__unique_label: if col in self.__categorical_column: unique_value = train_df[col].unique() temp_res1 = [] for u in unique_value: temp_res1.append(category_prob(train_df, col, u, self.__target, label, l=1)) temp_res.append(temp_res1) else: temp_res.append(estimate_mean_std(train_df, col, self.__target, label)) reference_dict[col] = temp_res self.__reference_dict = reference_dict prior_probs = [] for label in self.__unique_label: prior_prob = estimate_target_prob(train_df, self.__target, label) prior_probs.append(prior_prob) self.__prior_probs = prior_probs def get_reference_dict(self): return self.__reference_dict def predict(self, new_data): object_value = [0]*len(self.__unique_label) for idx in new_data.index[:-1]: value = new_data[idx] reference_value = self.__reference_dict[idx] if idx in self.__categorical_column: for i, r in enumerate(reference_value): ## if category, reference value is the value of probability value = int(value) ## 표준화를 하는 과정에서 다른 열의 정수 값이 float로 바뀌기 다시 정수로 바꿔줌 object_value[i] += np.log(r[value]) else: for i, r in enumerate(reference_value): ## if continuous, reference value contains (mean, std) object_value[i] += np.log(norm.pdf(value, r[0], r[1])) for i in self.__unique_label: object_value[i] += np.log(self.__prior_probs[i]) max_object_value = max(object_value) max_idx = object_value.index(max_object_value) return max_idx
line 2~7
클래스 초기화 함수이다. 나는 클래스를 생성할 때 출력 변수의 라벨(unique_label)과 출력 변수(target) 그리고 범주형 변수(categorical_column)가 무엇인지 알려주도록 했다. 출력 변수의 라벨은 학습 데이터를 이용해서 자동적으로 알 수 있는데 굳이 왜 넣었냐 할 수 있겠지만 운 좋게 학습 데이터에 없는 라벨이 테스트 데이터에도 있을 수 있으므로 전체 데이터에 대한 출력 변수 라벨을 넣어주도록 한 것이다.
line 9~30
나이브 베이즈 분류기의 훈련을 담당하는 함수이다. 여기서 훈련을 한다는 것은 학습 데이터를 이용하여 출력 라벨의 확률 P(y=j)을 추정(line 26~30)하고 각 독립변수별 조건부 확률 P(X|y=j)를 추정(line 10~24)하는 것이다. 이렇게 추정한 값들은 예측 단계에서 변하지 않으므로 조건부 확률 분포의 추정값들은 __reference_dict 필드에 담아서 예측 단계에서 참조할 수 있도록 설정했다. 왜냐하면 이렇게 하지 않고 예측 단계에서 매번 똑같은 값들을 추정할 때 테스트 시간이 굉장히 길어지기 때문이다.
line 36~57
새로운 독립변수를 받아서 예측 라벨을 출력해주는 함수이다. 처음에 출력 변수의 라벨 개수를 길이로 갖는 리스트를 모두 0으로 초기화해주고(line 37) 독립변수의 유형이 범주형인지 연속형인지 확인하고 그에 따라 조건부 확률 값을 로그함수를 씌워서 더해준다(line 38~50). 그리고 출력 변수의 확률도 로그함수를 씌워서 더해준다(line 53~54). 그리고 최종 리스트 object_value에서 최대값을 갖는 인덱스를 예측 라벨로 리턴한다(line 55~57).
다음은 학습 데이터와 테스트 데이터를 나눠주는 함수이다. 전체 데이터에서 split_ratio 만큼 테스트 데이터, 나머지는 학습 데이터로 분할한다.
def split_test_train_data(df, split_ratio): num_test_df = int(len(df)*split_ratio) idx_test_df = random.sample(df.index.tolist(),num_test_df) test_df = df.loc[idx_test_df].reset_index(drop=True) train_df = df.drop(idx_test_df).reset_index(drop=True) return train_df, test_df
이제 전체 데이터를 학습 데이터와 테스트 데이터로 분할하고 연속형 변수에 대해서는 표준화를 해준다. 그리고 출력 변수(target)를 설정하고 NaiveBaysClassifier 클래스를 생성한다.
random.seed(110) split_ratio = 0.2 train_df, test_df = split_test_train_data(df,split_ratio) ## split train, test dataset for col in train_df.columns[:-1]: if col not in categorical_column: mean = train_df[col].mean() std = train_df[col].std() train_df[col] = train_df[col].map(lambda x: (x-mean)/std) test_df[col] = test_df[col].map(lambda x: (x-mean)/std) target = 'income' unique_label = df[target].unique() NBC = NaiveBaysClassifier(unique_label,target,categorical_column)
나이브 베이즈 분류기를 학습해보자.
NBC.train(train_df) ## 나이브 베이즈 분류기 학습
내가 만든 분류기의 성능을 테스트할 시간이다. 먼저 훈련 정확도(train accuracy)를 구해보자.
## train accuracy total_sum = 0 for i, new_data in tqdm(train_df.iterrows(), total=len(train_df)): if new_data[target] == NBC.predict(new_data): total_sum += 1 accuracy = total_sum/len(train_df)
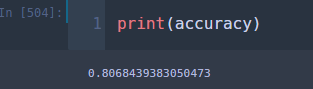
80.68%가 나왔다.
이제 테스트 정확도(Test accuracy)를 구해보자.
## test accuracy total_sum = 0 for i, new_data in tqdm(test_df.iterrows(), total=len(test_df)): if new_data[target] == NBC.predict(new_data): total_sum += 1 accuracy = total_sum/len(test_df)
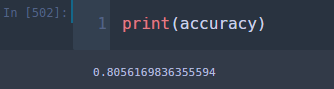
80.56% 이는 훈련 정확도보다는 조금 낮은 수준이다. 이게 과연 좋은 걸까? 적어도 나이브 베이즈 분류기가 나쁘지 않다고 말할 수 있으려면 학습 데이터에서 출력 변수 라벨의 빈도수가 높은 쪽을 찍는 것보다는 좋아야 할 것이다.
## vote majority 학습데이터에서 가장 많이 나온 라벨로 예측하는 거 mode = train_df[target].mode()[0] ## 1 print(len(test_df[test_df[target]==mode])/len(test_df))

나이브 베이즈 분류기의 정확도가 75.13% 보다는 높으므로 그렇게 나쁘지 않다고 볼 수 있다.
2. 출력 변수가 3개 이상의 클래스인 경우
Adult Data Set은 출력 라벨의 개수가 2개였다. 이번엔 3개 이상의 출력 변수 라벨을 갖는 데이터에 대해서 분류기의 성능을 테스트해보고자 한다.
Glass Identification Data Set을 불러오자.
## https://archive.ics.uci.edu/ml/datasets/glass+identification df = pd.read_csv('glass.csv')
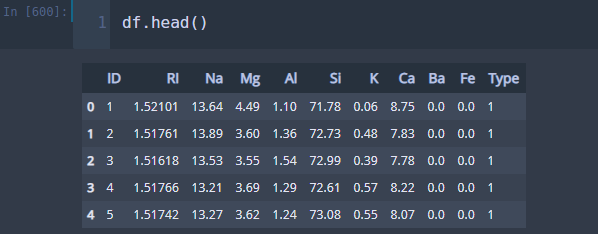
간단하게 데이터 전처리를 해주자. 필요 없는 열을 제거하고 출력 변수(Type) 라벨을 바꿔준다.
## 필요없는 열 제거 df.drop('ID',axis=1,inplace=True) ## category to num res_dicts = dict() for col in ['Type']: res, res_dict = convert_label(df,col) res_dicts[col] = res_dict df[col] = res
다음으로 학습 데이터와 테스트 데이터를 나눠준다. 여기서는 sklearn에서 제공하는 train_test_split을 썼다. 직접 구현하기 어렵다면 train_test_split 써보자.
그리고 이번 데이터는 독립변수가 모두 연속형이다. 연속형 변수는 표준화를 해주자.
출력 라벨의 중복되지 않는 값을 구하고 NaiveBaysClassifier 클래스를 생성한다.
unique_label = y.unique() NBC_multiclass = NaiveBaysClassifier(unique_label,target)
나이브 베이즈 분류기를 학습해준다.
NBC_multiclass.train(train_df) ## 나이브 베이즈 분류기 학습
성능을 테스트해보자. 먼저 훈련 정확도를 확인해보도록 하자.
## train accuracy total_sum = 0 for i, new_data in tqdm(train_df.iterrows(), total=len(train_df)): if new_data[target] == NBC_multiclass.predict(new_data): total_sum += 1 accuracy = total_sum/len(train_df)
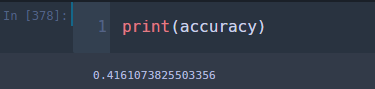
41.61% ... 훈련 정확도가 이 정도면 테스트 정확도는 도대체 얼마일까 ㄷㄷ;;
## test accuracy total_sum = 0 for i, new_data in tqdm(test_df.iterrows(), total=len(test_df)): if new_data[target] == NBC_multiclass.predict(new_data): total_sum += 1 accuracy = total_sum/len(test_df)
40%다 ...
## vote majority 학습데이터에서 가장 많이 나온 라벨로 예측하는 거 mode = train_df[target].mode()[0] ## 1 print(len(test_df[test_df[target]==mode])/len(test_df))

오.. 그래도 많은 쪽을 찍는 것(35.38%) 보다는 좋게 나왔다. ...
모든 독립변수가 연속형인 경우 sklearn에서 제공하는 GaussianNB을 이용하여 손쉽게 나이브 베이즈 분류기를 학습할 수 있다.
## sklearn 이용하기 nb = GaussianNB() nb.fit(X_tr, y_tr) ## 나이브 베이즈 분류기 학습
성능을 확인해보자. 과연 내가 구현한 것보다 좋을 것인가? 두근두근.. 먼저 훈련 정확도 먼저.
## train accuracy nb.score(X_tr, y_tr)
!! 나의 나이브 베이즈 분류기(41.61%)가 sklearn에서 제공하는 분류기(38.26%) 보다 더 좋다?!. 이번엔 테스트 정확도를 구해보자.
## test accuracy nb.score(X_te, y_te)
오잉? 나의 나이브 베이즈 분류기(40%)가 sklearn에서 제공하는 분류기(33.85%) 보다 더 좋다?!. 신기하다. 이거 뭔가 이유가 있겠지 싶어서 sklearn 문서를 보았다.
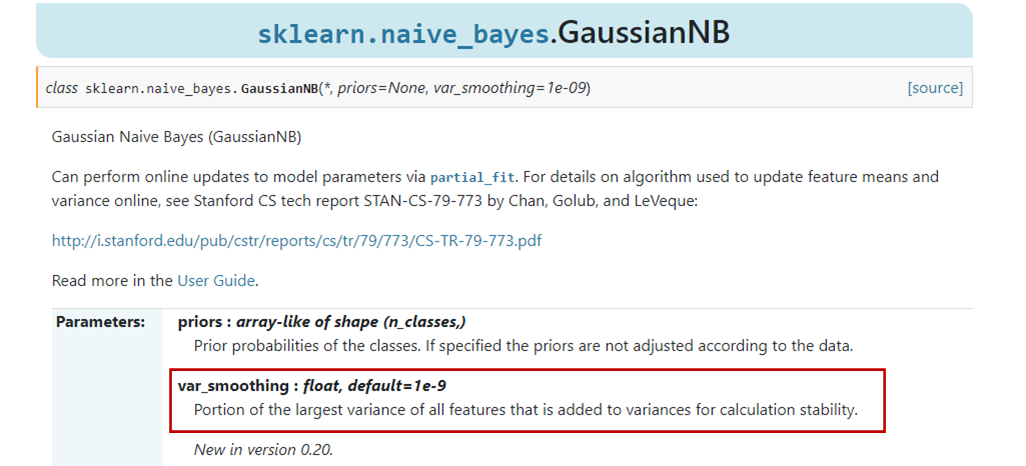
확인해보니 연속형 독립 변수인 경우 분산을 추정(이는 표준편차를 추정하는 것과 동일하다고 생각하면 된다)하게 되는데 분산 추정값이 0이 되는 걸 방지해주는 값인 것 같다. 이러한 점 때문에 성능에서 차이가 난 것 같다(역시 sklearn을 개발하신 분들이 이렇게 허술할 리 없지!). 독립변수가 모두 연속형이라면 sklearn에서 제공하는 GussianNB를 사용해보자. 나는 해놓은 게 있으니 두 개 다 써보고 좋은 거를 선택해야지 헤헤
3. 다항 나이브 베이즈 분류기 구현하기
이번에 독립변수가 특정 범주에 대한 빈도수인 경우에 나이브 베이즈 분류기(다항 나이브 베이즈 분류기)를 구현해보자. 이를 위한 데이터(SMS Spam Collection Data Set)를 불러오자. 불러올 때 인코딩 방식을 지정하지 않으면 오류가 발생하므로 주의하자.
df = pd.read_csv('spam.csv',encoding = "ISO-8859-1")
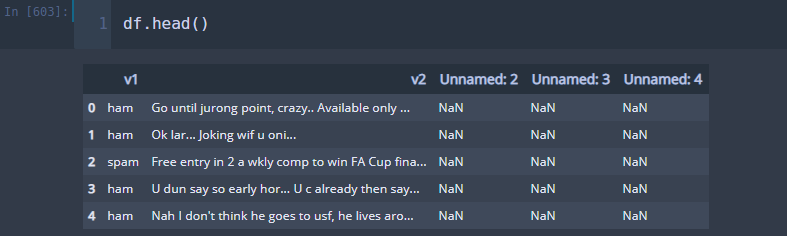
여기서도 간단한 데이터 전처리를 해주자. 필요 없는 열을 제거하고 출력 변수(v1)의 라벨을 바꿔준다. 그리고 출력 변수를 맨 마지막 열에 있도록 해준다.
## 필요없는 열 제거 df.dropna(inplace=True,axis=1) ## category to num res_dicts = dict() for col in ['v1']: res, res_dict = convert_label(df,col) res_dicts[col] = res_dict df[col] = res df = df[['v2','v1']]
몇 가지 필요한 함수를 먼저 만들어준다. 다음은 문장을 의미 있는 단위로 쪼개 주는 함수이다. 의미 있는 최소 단위는 단어이므로 문장을 단어 단위로 쪼개는 함수를 만들어 준다.
def tokenize(message): message = message.lower() all_words = re.findall("[a-z0-9']+", message) return list(set(all_words))
다음으로 출력 변수의 라벨에 따라 학습 데이터에서 출현한 단어와 출현 횟수를 계산하는 함수를 만든다.
def count_words(df,unique_label,column,target): counts = defaultdict(lambda : [0]*len(unique_label)) for _, row in df.iterrows(): for word in tokenize(row[column]): counts[word][row[target]] += 1 return counts
다음은 새로운 메시지에서 출현한 단어와 횟수를 계산한다. 위에서 만든 함수는 학습 데이터 전체에 대하여 출현한 단어와 출현 횟수를 구하는 것이고 이 함수는 메시지 하나에 대하여 단어와 횟수를 구하는 것이다.
def count_row_words(new_data): counts = defaultdict(lambda: 0) for word in tokenize(new_data): counts[word] += 1 return counts
다음은 다항 나이브 베이즈 분류기를 학습하고 예측할 수 있는 MutinomialNaiveBayesClassifier 클래스를 만든 것이다. 원리는 앞서 선보인 NaiveBaysClassifier 클래스와 흡사하므로 설명은 생략한다.
class MutinomialNaiveBayesClassifier: def __init__(self,unique_label,target,column): self.__reference_counts = None self.__prior_probs = None self.__target = target self.__unique_label = unique_label self.__column = column def train(self, train_df): reference_counts = count_words(train_df, self.__unique_label, \ self.__column, self.__target) self.__reference_counts = reference_counts prior_probs = [] for label in self.__unique_label: prior_prob = estimate_target_prob(train_df, self.__target, label) prior_probs.append(prior_prob) self.__prior_probs = prior_probs def get_reference_counts(self): return self.__reference_counts def predict(self, new_data): new_data = new_data[column] new_data = count_row_words(new_data) ## new_data must be a dictinary whose key 'word' value 'count' object_value = [] for label in self.__unique_label: ## for each label, generate dictionary whose key 'word' value 'count' temp_counts = {k: v[label] for k, v in self.__reference_counts.items()} cum_word_count = 0 numerators = [] train_word_counts = [] ## word count in train data set new_counts = [] ## word count in a new data for word, count in new_data.items() : if word not in temp_counts.keys(): train_word_count = 0 else: train_word_count = temp_counts[word] new_counts.append(count) numerators.append(train_word_count + l) cum_word_count += train_word_count denominator = cum_word_count + l*len(self.__reference_counts.keys()) probs = np.array(numerators)/denominator log_sum = 0 for i, p in enumerate(probs): log_sum += new_counts[i]*np.log(p) object_value.append(log_sum) for i in self.__unique_label: object_value[i] += np.log(self.__prior_probs[i]) max_object_value = max(object_value) max_idx = object_value.index(max_object_value) return max_idx
이제 다항 나이브 베이즈 분류기를 실험해보자. 먼저 MutinomialNaiveBayesClassifier 클래스를 생성한다.
## MutinomialNaiveBayesClassifier 클래스 생성 target = 'v1' unique_label = train_df[target].unique() column = 'v2' MNBC = MutinomialNaiveBayesClassifier(unique_label,target, column)
다항 나이브 베이즈 분류기를 학습한다.
MNBC.train(train_df) ## 다항 나이브 베이즈 분류기 학습
성능을 테스트할 시간이 왔다. 훈련 정확도를 계산해보자.
## train accuracy total_sum = 0 for i, new_data in tqdm(train_df.iterrows(), total=len(train_df)): if new_data[target] == MNBC.predict(new_data): total_sum += 1 accuracy = total_sum/len(train_df)
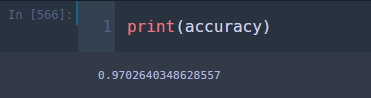
97.02% 나왔다. 훈련 정확도는 믿을게 못된다. 이제 테스트 정확도를 계산해보자.
## test accuracy total_sum = 0 for i, new_data in tqdm(test_df.iterrows(), total=len(test_df)): if new_data[target] == MNBC.predict(new_data): total_sum += 1 accuracy = total_sum/len(test_df)
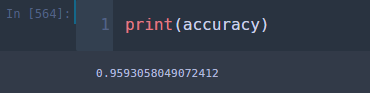
??? 95.93% 이 정도면 나쁘지 않은 것 같다.
## vote majority 학습데이터에서 가장 많이 나온 라벨로 예측하는 거 mode = train_df[target].mode()[0] ## 1 print(len(test_df[test_df[target]==mode])/len(test_df))

단순히 많은 쪽을 찍는 것(86.71%)보다도 성능이 좋게 나왔다.
데이터가 문서 내용과 해당 문서 카테고리 형식으로 주어졌다면 sklearn에서 제공하는 MultinomialNB을 이용하여 다향 나이브 베이즈 분류기를 학습할 수 있다. CounterVectorizer를 이용하여 각 메시지를 단어의 출현 횟수로 이루어진 행렬을 중간에 만들어줘야 한다.
X_tr = train_df['v2'] y_tr = train_df['v1'] X_te = test_df['v2'] y_te = test_df['v1'] ## 메시지를 단어별 횟수 행렬로 변환한다. cv = CountVectorizer() cv.fit(X_tr) ## 데이터 변환 X_tr = cv.transform(X_tr) X_te = cv.transform(X_te) ## 다항 나이브 베이즈 분류기 학습 MNBC1 = MultinomialNB() MNBC1.fit(X_tr, y_tr)
이렇게 만들어진 분류기의 정확도는 얼마일까? 훈련 정확도 먼저 계산해보자.
## train accuracy MNBC1.score(X_tr, y_tr)
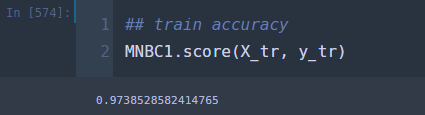
!! 97.39% !! 여기서 구현한 분류기의 성능(97.02%) 보다 약간 높다. 이번엔 테스트 정확도를 확인해보자.
## test accuracy MNBC1.score(X_te, y_te)
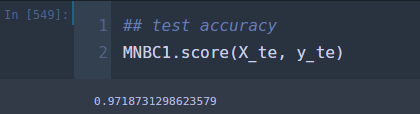
!! 97.18% 내가 구현한 분류기의 성능(95.93%) 보다 높다. 앞으로는 이거 써야겠다 ㅋㅋ.
그건 그렇고 어디에서 차이가 발생한 걸까? 다항 나이브 베이즈를 학습하는데 필요한 단어의 수에서 차이가 났다.

나는 분류기를 학습하는데 7317개의 단어를 사용했다. 하지만 MultinomialNB는 214개의 단어를 사용했다.

데이터를 많이 사용할수록 좋은 거 아닌가? 아니었다. 내가 사용한 단어는 의미 없는 단어가 아주 많았다.
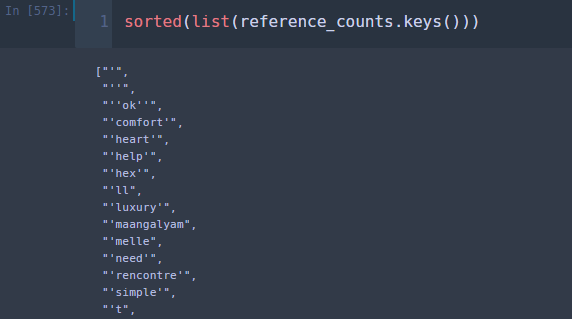
위에서 보는 바와 같이 따옴표가 들어가 있다. ㄷㄷ;; 반면 MultinomialNB는 상대적으로 의미 있는 단어가 훨씬 많았다.
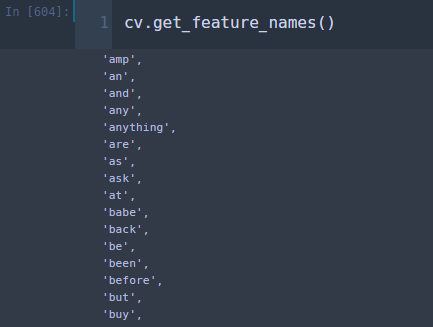
이런 부분이 성능의 차이를 유발한 것이다. 이는 토큰화(tokenize) 방식에 차이가 있기 때문인데 여기서 사용한 방식은 아주 간단한 것이라서 그렇다. 아무튼 결론은 MultinomialNB 쓰자 ^^;;
3. 나이브 베이즈 분류기 장단점
- 장점 -
1) 만약 독립 변수들이 조건부 독립이라는 가정을 만족한다면 나이브 베이즈 분류기는 최적 분류기(베이즈 분류기)가 된다. 따라서 이를 쓰지 말아야할 이유가 없어지는 것이다.
2) 조건부 독립 가정으로 인하여 나이브 베이즈 분류기를 추정하기 위한 계산이 매우 간단해진다. 왜냐하면 추정해야할 모수의 개수가 줄어들기 때문이다. 예를 들어 p차원 연속형 독립변수의 분포가 p차원 정규분포라고 하자. 조건부 독립 가정이 없다면 추정해야할 모수는 몇개일까? p개의 평균과 p개의 분산 그리고 p(p-1)/2개의 공분산을 추정해야하므로 총 개수는
p + p + \frac{p(p-1)}{2} = 2p + \frac{p(p-1)}{2}
가 된다.
반면 조건부 독립을 가정하게 되면 변수 하나 당 평균과 분산 2개의 모수 추정이 필요하므로 2p개만 있으면 된다. 무려 p(p-1)/2개 만큼의 모수를 줄여준다.
p개의 범주형 독립변수인 경우에도 마찬가지이다. 조건부 독립 가정이 없다면 p개의 독립변수가 각각 k개의 범주를 갖는다고 할때 구해야하는 확률값은 k^p이다. 왜냐하면 아래의 조건부 확률에서 가질 수 있는 값이 k^p개라서 그렇다.
P(X_1=k_1, X_2=k_2, \ldots, X_p=k_p|y=j)\tag{11}
만약 조건부 독립이라 가정하면 (11)은 다음과 같아진다.
P(X_1=k_1|y=j)P(X_2=k_2|y=j)\cdots P(X_p=k_p|y=j)\tag{12}
(12) 추정해야할 확률값은 확률값 하나당 k이고 변수의 개수가 p개 있으므로 kp개로 줄어든다. 엄청난 차이다. ㄷㄷ;;
3) 기본 베이스 모형으로 사용할 수 있다. 즉, 분류 문제에서 내가 개발한 모델의 성능을 비교하기 위한 베이스로써 나이브 베이즈 분류기를 사용할 수 있다.
4) 나이브 베이즈 분류기가 정교하게 만들어진 예측 분류기보다 오히려 성능이 좋을 때가 있다고 한다. 왜냐하면 조건부 독립이라는 가정이 실제 맞지 않는 경우 독립변수의 조건부 확률에 편향(Bias)이 생기는데 편향이 생기는 대신 분산이 줄어들어 예측하는데 오히려 유리할 수 있다고한다.
5) 관련 없어보이는 설명 변수가 있어도 성능에 큰 영향을 주지 않는다고 알려져 있다. 위에서 스팸을 분류하는 예제에서 내가 구현한 다항 베이즈 분류기는 쓸데 없는 단어가 많이 들어갔지만 의미 있는 단어들로 이루어진 다항 베이즈 분류기와 성능 차이가 많이 나지 않았다.
- 단점 -
1) 조건부 독립이라는 가정이 현실적이지 않다. 대부분의 경우 독립변수들 간에는 어느 정도 상관관계가 있기 때문이다. 이런 상황에서 나이브 베이즈 분류기는 별로 좋지 않을 수 있다.
2) 나이브 베이즈 분류기는 각 독립변수가 출력 변수에 미치는 영향이 서로 다른 경우, 즉 어떤 독립변수는 출력 변수에 영향을 지대하게 미치고 나머지는 미미할 때 이러한 영향력을 나이브 베이즈 분류기는 잘 반영하지못한다는 단점이 있다.
마치며 ~
이번 포스팅에서는 나이브 베이즈 분류기에 대해서 알아보았는데 간단한 모형이지만 생각보다 고려할 것들이 많았다. 그리고 나이브 베이즈 분류기가 단순하기 때문에 좋은 분류기가 아니라고 생각하는 분들이 많은데 의외로 좋은 성능을 보일 때가 많다고 한다. 꼭 복잡한 모형만이 만능은 아닌 것 같다. 나이브 베이즈 분류기는 위대하다~!!
참고자료
Naive Bayes Classifier from Scratch - ybigta-data-science.readthedocs.io/en/latest/6_Data_Science_from_Scratch/03_Naive%20Bayes%20Classifier/
Naive Bayes Classifier in Python - www.kaggle.com/prashant111/naive-bayes-classifier-in-python
Trevor Hastie 외 2명 - The Elements of Statistical Learning
Bayes Classifier and Naive Bayes - www.cs.cornell.edu/courses/cs4780/2018fa/lectures/lecturenote05.html

'통계 > 머신러닝' 카테고리의 다른 글
| 6. Least Absolute Deviation Regression에 대해서 알아보자 with Python (0) | 2021.01.26 |
|---|---|
| [머신 러닝] 5. EM(Expectation-Maximization) Algorithm(알고리즘)에 대해서 알아보자. (0) | 2021.01.19 |
| [머신 러닝] 3. 베이즈 분류기(Bayes Classifier) (0) | 2020.12.21 |
| [머신 러닝] 2. K-최근접 이웃 분류기(K-Nearest Neighbor Classifier)에 대하여 알아보자 with Python (0) | 2020.12.15 |
| [머신 러닝] 1. 소개 (0) | 2020.11.27 |





댓글