이번 포스팅에서는 k-근접 이웃 분류기에 대해서 알아보고자 한다. k-근접 이웃 분류기는 실제로 잘 활용되지는 않지만 데이터를 이용하여 분류하는 기본적인 과정을 이해하는데 유용하며 때에 따라서 다른 예측 분류기의 비교를 위한 기초 모형이 될 수 있다.
이번 포스팅에서 다루는 내용은 다음과 같다.
2. k-근접 이웃 분류기 모의 실험 with Python
1. k-근접 이웃 분류기란 무엇인가
- 정의 -
k-근접 이웃 분류기(k-Nearest Neighbor : kNN)는 특정 입력 데이터가 주어졌을 때 입력 데이터와 가까운 k개의 데이터를 이용하여 예측하는 모형이다.
우리에게 데이터 $(\tilde{x}_i, y_i), \;\;i=1,\ldots,n$ 이 있다. 여기서 $\tilde{x}_i = (x_{1i}, x_{2i}, \ldots, x_{pi})^t \in \mathbb{R}^p$, 즉 $p$ 차원 (연속형) 입력 변수이고, $y_i$는 출력 변수이다. 지금은 분류에 대한 문제를 다룰 것이므로 $y_i \in \{1, 2, \ldots, J\}$, 즉 $J$개의 카테고리가 있다고 하자. 그리고 $T = \{(\tilde{x}_i, \;y_i) \;:\;i=1, 2, \ldots, n\}$라고 하자(즉, 학습 데이터이다).
이제 앞의 정의를 수식을 이용하여 다시 풀어써보자. 먼저 입력 데이터 $\tilde{x} = (x_1, x_2, \ldots, x_p)^t$가 주어졌다(입력 데이터는 $T$에 속할 수도 있고 아닐 수도 있다)고 하자. 그렇다면 k-근접 이웃 분류기는 다음과 같이 $\hat{y}(\tilde{x})$를 예측한다.
$$\DeclareMathOperator*{\argmaxA}{argmax}\hat{y}(\tilde{x}) = \argmaxA_{j\in\{1, 2, \ldots, J\}} \underbrace{\frac{1}{k}\sum_{i : \tilde{x}_i\in N_k(\tilde{x})}I(y_i=j)}_{(2)}\tag{1}$$
여기서 $N_k(\tilde{x})$는 $\tilde{x}$와 가까운 $k$개 $\tilde{x}_i$의 집합, $I(A)$는 $A$가 참이면 1, 거짓이면 0을 출력하는 함수이다. 이때 $k$는 미리 지정해줘야 하는 값이라는 점을 주목하자. 만약 $y_i$가 연속형이고 $I(y_i=j)$를 $y_i$로 바꾸면 식 (1)은 회귀 모형이된다. 즉, kNN은 분류, 회귀 모형에 다 사용할 수 있는 굉장히 유연한 모형이다.
- 예제 -
위 수식을 그림을 이용하여 표현해보자. 여기서는 k = 4라고 가정하자.

먼저 위와 같이 데이터가 존재하고 있다. 파랑 = 1, 빨강 = 2, 보라 = 3이라고 하자. 즉, 카테고리의 개수는 3개이며 $y_i \in \{1, 2, 3\}$이다.

우리에게 입력 데이터가 주어졌다. 위 그림에서 초록색 x로 표시했다. 이것이 식 (1)에서 $\tilde{x}$
에 해당한다.
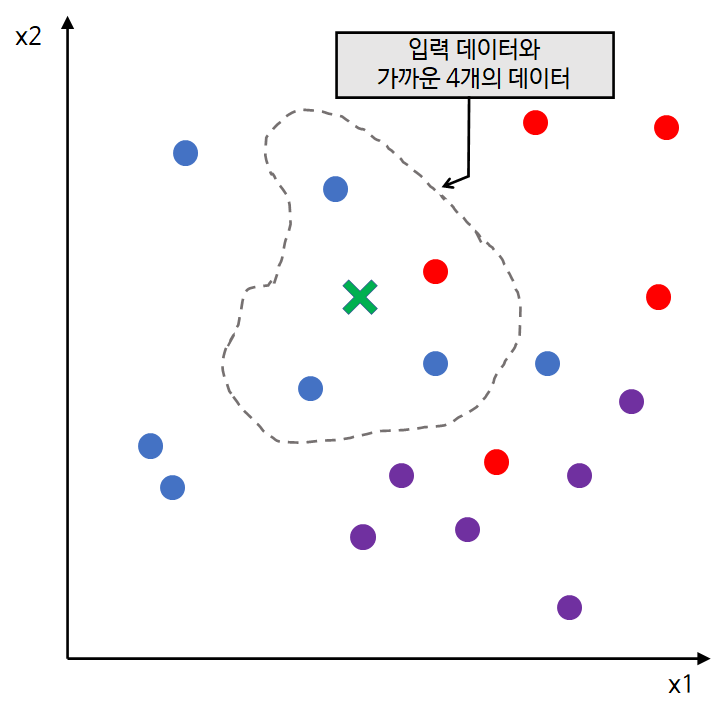
다음으로 입력 데이터로부터 가장 가까운 k(=4) 개 데이터를 구한다. 위 그림에서 회색 점선 안에 파랑 점 3개와 빨간 점 1개가 이에 해당하며 이것이 식 (1)에서 $N_k(\tilde{x})$에 해당한다.

이제 식 (1)에서 (2)에 해당하는 값을 계산해야 한다. 카테고리가 3개 있으므로 3개의 경우로 나누어 계산해야 한다.
1) 파랑인 경우 $(j=1)$.
$$\frac{1}{k}\sum_{i : \tilde{x}_i\in N_k(\tilde{x})}I(y_i=j) = \frac{1}{4}\cdot3 = \frac{3}{4}$$
2) 빨강인 경우 $(j=2)$.
$$\frac{1}{k}\sum_{i : \tilde{x}_i\in N_k(\tilde{x})}I(y_i=j) = \frac{1}{4}\cdot1 = \frac{1}{4}$$
3) 보라인 경우 $(j=3)$.
$$\frac{1}{k}\sum_{i : \tilde{x}_i\in N_k(\tilde{x})}I(y_i=j) = \frac{1}{4}\cdot0 = 0$$
이 3개의 값에 대해서 최대가 되는 $j$는 1(파랑)인 것을 알 수 있다. 따라서 $\hat{y}(\tilde{x})=1$ 이 된다.
여기서는 최대값을 갖는 카테고리가 1이기 때문에 예측값을 1로 정하면 되지만 아래 그림과 같이 카테고리가 동률인 경우가 발생할 수 있다.

이 경우에 예측값을 파랑으로 할지 빨강으로 할지 고민이 된다.

이런 상황에서는 가장 합리적인 선택을 하면 된다. 입력 데이터와 가장 가까운 점을 찾고 그 점에 대한 카테고리를 예측값으로 한다. 위 그림에서 입력 데이터와 가장 가까운 점은 파랑점이므로 예측값을 파랑으로 정하면 된다.
하지만 아직 뭔가 해결이 안 된 것 같은 찝찝함이 남아있다. 왜냐하면 아래 그림과 같이 가장 가까운 거리마저 동률이 발생하는 경우가 있기 때문이다.
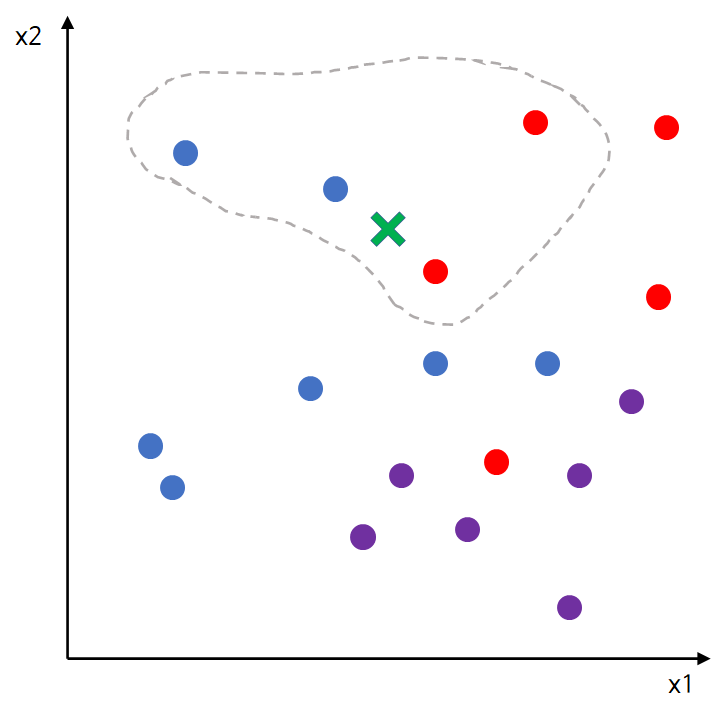
위 그림에서 입력 데이터와 가장 가까운 점은 파랑점과 빨강 점 두 개이다.
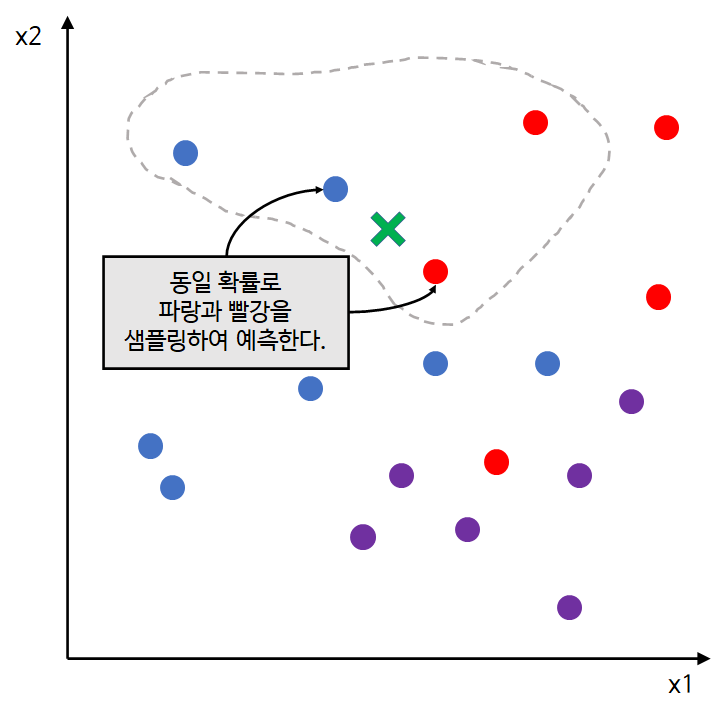
이때에는 파랑과 빨강을 동일 확률(1/2)로 샘플링하여 예측하면 된다.
- k의 선택 -
앞서 k는 미리 지정해줘야 하는 값이라고 이야기했다. 하지만 이왕이면 더 좋은 값을 선택하고 싶은 것이 사람 마음일 것이다. 이때에는 교차 검증(cross validation)을 이용한다. 교차 검증에 대해서는 추후 포스팅하기로 하고 여기서는 간단한 방법을 소개한다.
1) 먼저 k의 후보군을 정한다. 1부터 학습 데이터 개수-1까지로 한다. 데이터의 개수가 많다면 k는 1부터 $\sqrt{n}$까지 정한다. 만약 k가 학습 데이터 개수와 같다면 예측값은 항상 전체 학습 데이터 중에서 가장 높은 빈도수를 가지는 라벨을 출력하게 된다.
2) 검증 데이터를 만들고 각 k에 대하여 검증 데이터에 대한 kNN의 에러율을 구한다.
3) 에러율이 가장 낮은 k를 선택한다.
다음의 모의실험에서 k를 선택하는 부분이 나오니 지금 이해 안 가더라도 괜찮다.
또한 교차 검증법을 사용하지 않고 k를 $\sqrt{n}$에 가까운 정수로 사용하는 것도 권장하고 있다(참고).
2. k-근접 이웃 분류기 모의실험 with Python
The Element of Statistical Learning(Trevor Hastie 외 2명)에서 2.3.3의 모의실험을 바탕으로 수행한다. 코드 설명은 중요한 부분만 하려고 한다.
먼저 이번 포스팅에서 필요한 모듈을 임포트 한다.
import numpy as np
import matplotlib.pyplot as plt
import random
import pandas as pd
from tqdm import tqdm
from collections import Counter
다음으로 데이터를 생성한다.
## pick cluster
random.seed(100)
blue_means = np.random.multivariate_normal([1,0],[[1,0],[0,1]],10)
orange_means = np.random.multivariate_normal([0,1],[[1,0],[0,1]],10)
num_samples = 5100
blue_samples = []
orange_samples = []
for i in range(num_samples):
blue_mk = random.sample(list(blue_means),k=1)[0]
blue_sample = np.random.multivariate_normal(blue_mk,[[1/5,0],[0,1/5]],1)
blue_samples.append(np.squeeze(blue_sample))
orange_mk = random.sample(list(orange_means),k=1)[0]
orange_sample = np.random.multivariate_normal(orange_mk,[[1/5,0],[0,1/5]],1)
orange_samples.append(np.squeeze(orange_sample))
## generate train and test data
num_train_samples = 100
train_samples = (blue_samples[:num_train_samples], orange_samples[:num_train_samples])
test_samples = (blue_samples[num_train_samples:], orange_samples[:num_train_samples:])
## Reforming train data
X = []
y = []
for j in range(len(train_samples)):
for data in train_samples[j]:
y.append(j)
temp = []
temp += [data[0],data[1]]
X.append(temp)
y = np.array(y)
X = np.array(X)
df = pd.DataFrame(X,columns=['x1','x2'])
df['y'] = y이제 학습 데이터의 분포를 확인해보자.
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
colors = ['#4accf0','orange']
for j in range(len(train_samples)):
x1_s = []
x2_s = []
for data in train_samples[j]:
x1_s.append(data[0])
x2_s.append(data[1])
plt.scatter(x1_s,x2_s,s=80, facecolors='none', edgecolors=colors[j])
num_grid = 100
grid_x1 = np.linspace(min(df['x1']),max(df['x1']),num_grid+1)
grid_x2 = np.linspace(min(df['x2']),max(df['x2']),num_grid+1)
plt.xlim(min(df['x1']),max(df['x1']))
plt.ylim(min(df['x2']),max(df['x2']))
plt.show()

위 그림은 랜덤 샘플링을 기반으로 하였기 때문에 나와 다를 수 있다. 이제 kNN 모형을 구현해보자.
def knn_predict(data,X,y,k=1):
distances = []
for val in X:
distance = np.linalg.norm(data-val)
distances.append(distance)
distances = np.array(distances)
if k < len(distances):
idx = np.argpartition(distances,k)
prediction = Counter(y[idx[:k]]).most_common()[0][0]
else:
prediction = Counter(y).most_common()[0][0]
return prediction
line 1
입력 데이터를 data, 학습 데이터의 입력 데이터를 X, 라벨을 y, 그리고 k를 인자로 받도록 했다. knn_predict 함수는 주어진 data에 대해서 가까운 k개의 라벨을 본 뒤 가장 많은 라벨을 예측값으로 던져주도록 설계한다(동률 처리는 하지 않았다 귀찮아서).
line 2~5
입력 데이터와 학습 데이터의 입력 데이터 간 거리를 구한다. 거리의 측도는 Euclidean Norm을 이용했다.
line 9~10
이제 작은 순서대로 k개의 라벨을 구해야 한다. 먼저 위에서 구한 거리에서 가장 작은 k개에 해당하는 인덱스를 구해야 한다. 이를 위해 np.argpartition을 이용한다(line 9). 이 함수는 첫 번째 인자로 받은 배열에서 가장 작은 k(두 번째 인자)개에 해당하는 인덱스를 앞으로 나머지를 오른쪽으로 하는 배열을 출력한다. 즉, np.argpartition이 리턴해주는 배열에서 앞쪽 k개까지가 우리가 구하는 인덱스가 된다. 그리고 이 인덱스에 해당하는 라벨 중에서 가장 높은 빈도수를 갖는 라벨을 prediction에 담는다(line 10).
line 12
만약 k가 학습 데이터 개수와 같다면 전체 라벨에서 가장 높은 빈도수를 가지는 라벨을 출력합니다.
이제 k값에 따른 학습 오차(Train error)를 살펴보자. 여기서는 k는 1, 15인 경우만 확인해보도록 하자.
## calculate train error
k = 1
predict = []
for j in range(len(df['x1'])):
data = [df['x1'][j],df['x2'][j]]
data = np.array(data)
predict.append(knn_predict(data,X,y,k))
predict = np.array(predict)
ktre = 1 - (y == predict).mean() ## train error

학습 오차가 0이 나왔다. 입력 데이터를 학습 데이터로 정하였고 k가 1인 경우 입력 데이터와 가장 가까운 학습 데이터는 입력 데이터 자기 자신이 되며 kNN의 예측값은 학습 데이터의 라벨과 같아진다. 따라서 학습 오차가 0이 되는 것이 당연한 결과이다. 이번엔 k를 15로 바꾸어서 해보자.
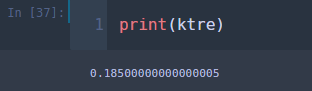
이번에는 학습 오차가 0.185가 나왔다.
이해를 돕기 위해 k=1, 15에 대한 Decision Boundary를 살펴보자.
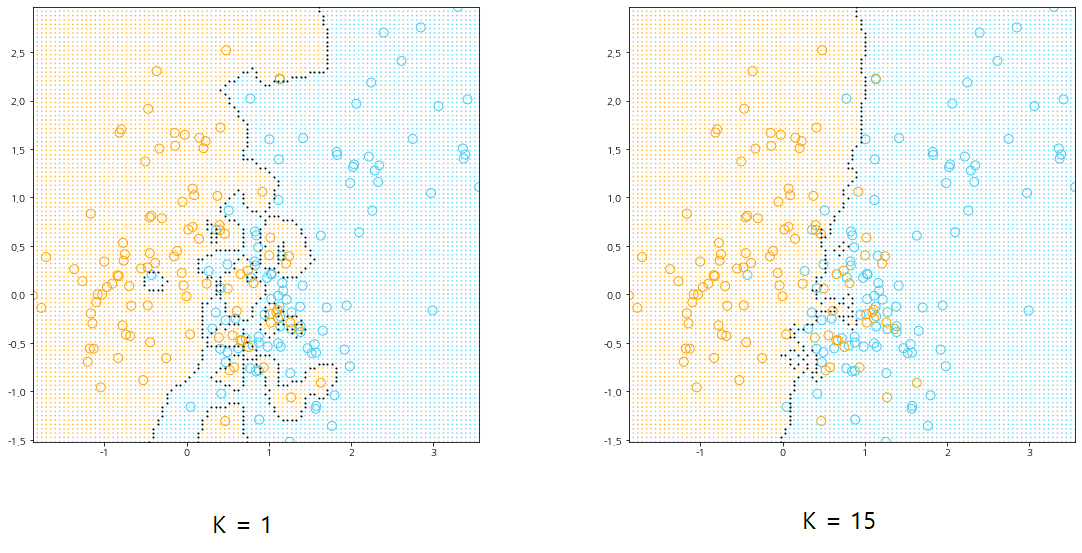
먼저 왼쪽 그림은 k가 1인 경우이다. 각 영역 안에는 해당 라벨에 대한 학습 데이터만 포함되어 있는 것을 알 수 있다. 예를 들어 파란 영역 안에는 파란 학습데이터만 포함되어 있다. 따라서 학습 데이터를 이용하여 학습 오차를 계산했을 때 0이 나온다. 오른쪽 그림은 k가 15인 경우이다. 왼쪽과 달리 각 영역에 다른 라벨에 대한 학습 데이터도 포함되어 있는 것을 알 수 있다. 예를들어 파란 영역안에 주황색 점들이 포함되어 있다. 따라서 학습 오차가 발생하게 된 것이다.
다음은 Decision Boundary를 그리기 위한 소스 코드이다.
def get_boundary(data,mod,target):
temp = []
for i in range(len(data)):
center = data[i]
if (i+1)%mod > 1:
direction = [i-1, i+1, i+mod, i-mod]
elif (i+1)%mod == 1:
direction = [i+1,i+mod,i-mod]
else:
direction = [i-1,i+mod,i-mod]
valid_idx = [x for x in direction if (x>=0 and x<=len(data)-1)]
for v in valid_idx:
if center != data[v]:
temp.append(i)
continue
res = []
for r in list(set(temp)):
if data[r] == target:
res.append(r)
return list(set(res))
num_grid = 100
grid_x1 = np.linspace(min(df['x1']),max(df['x1']),num_grid+1)
grid_x2 = np.linspace(min(df['x2']),max(df['x2']),num_grid+1)
temp_x1,temp_x2 = np.meshgrid(grid_x1,grid_x2)
positions = np.vstack([temp_x2.ravel(), temp_x1.ravel()])
k=1 ##or 15
grid_colors = []
for i in range(positions.shape[1]):
data = np.array([positions[1][i],positions[0][i]])
grid_colors.append(colors[knn_predict(data,X,y,k)])
boundary_idx = get_boundary(grid_colors,101,'#4accf0')
bx1 = positions[::-1][0][boundary_idx]
bx2 = positions[::-1][1][boundary_idx]
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
# ax = fig.add_subplot()
plt.xlim(min(df['x1']),max(df['x1']))
plt.ylim(min(df['x2']),max(df['x2']))
for j in range(len(train_samples)):
x1_s = []
x2_s = []
for data in train_samples[j]:
x1_s.append(data[0])
x2_s.append(data[1])
plt.scatter(x1_s,x2_s,s=80, facecolors='none', edgecolors=colors[j])
plt.scatter(*positions[::-1],color=grid_colors,s=0.25,zorder=-10)
plt.scatter(bx1,bx2,s=1,color='k')
plt.show()
이제 최적의 k를 선택해보자.
여기서는 k의 범위를 1~199(학습 데이터 개수-1)로 정했으며 각 k에 대하여 검증 데이터를 이용한 검증 오차, 학습 데이터를 이용한 학습 오차를 계산한다. 다음은 실행 코드이다(k를 선택하는 원리를 보여주기 위해 간단하게 구현하였고 엄밀한 교차 검증은 아니다). 시간이 좀 걸린다.
test_y = []
test_x1 = []
test_x2 = []
for j in range(len(test_samples)):
for data in test_samples[j]:
test_y.append(j)
temp = []
test_x1.append(data[0])
test_x2.append(data[1])
test_x1 = np.array(test_x1)
test_x2 = np.array(test_x2)
knn_train_error = []
knn_test_error = []
ks = range(1,200)
for k in tqdm(ks):
predict = []
for j in range(len(df['x1'])):
data = [df['x1'][j],df['x2'][j]]
data = np.array(data)
predict.append(knn_predict(data,X,y,k))
predict = np.array(predict)
ktre = 1 - (y == predict).mean()
knn_train_error.append(ktre)
t_predict = []
for j in range(len(test_x1)):
data = [test_x1[j],test_x2[j]]
data = np.array(data)
t_predict.append(knn_predict(data,X,y,k))
t_predict = np.array(t_predict)
kte = 1-(test_y == t_predict).mean()
knn_test_error.append(kte)
이를 시각화해보자.
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.plot(ks, knn_train_error,label='KNN Train Error')
plt.plot(ks, knn_test_error,label='KNN Validation Error')
plt.legend()
plt.xlabel('k')
plt.show()
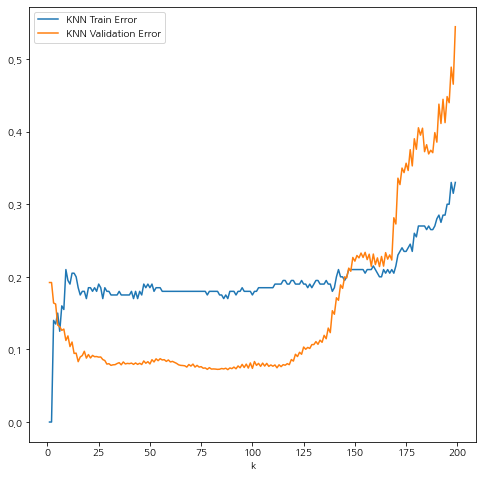
학습 오차는 k=1일 때 0부터 시작해서 k가 증가할수록 점점 커지는 경향이 있으며 검증 오차는 k가 증가할 수록 낮아지다가 나중에는 커지게 된다.
그리고 검증 오차를 최소화하는 k를 찾아보자.

k는 88일 때 가장 작은 검증 오차를 갖는다. 따라서 k는 88로 정한다.
3. 실제 데이터 적용해보기
이제 실제 데이터를 가지고 kNN 모형을 구축해보자. 여기서 다룰 데이터는 Iris 데이터를 이용하려고 한다.
먼저 필요한 모듈을 임포트한다.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from collections import Counter
from tqdm import tqdm
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
Iris 데이터를 불러온다.
iris = load_iris()
df = pd.DataFrame(np.c_[iris['data'],iris['target']],columns=iris['feature_names']+['label'])

다음으로 원 데이터를 학습 데이터, 검증 데이터, 테스트 데이터로 분할한다.
x = df[iris['feature_names']]
y = df['label']
train_x, test_x, train_y, test_y = train_test_split(x, y, test_size=0.2, random_state=42)
train_x, val_x, train_y, val_y = train_test_split(train_x, train_y, test_size=0.33, random_state=42)
검증 데이터를 통하여 최적 k를 찾아준다. 각 k별로 검증 오차(Validation error)를 시각화하는 코드도 추가했다.
knn_val_error = []
ks = range(1,len(train_x))
for k in tqdm(ks):
predict = []
for j in range(len(val_x)):
data = val_x.values[j]
data = np.array(data)
predict.append(knn_predict(data,train_x.values,train_y.values,k))
predict = np.array(predict)
ktre = 1 - (val_y == predict).mean()
knn_val_error.append(ktre)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
plt.plot(ks, knn_val_error)
plt.xlabel('k',fontsize=15)
plt.show()

min_val_error = min(knn_val_error)
opt_k = knn_val_error.index(min_val_error)+1 ## optimal k

최적 k는 10으로 선택한다. 이제 최적 k와 테스트 데이터를 이용하여 kNN의 모형을 평가한다.
k = opt_k
knn_test_error = []
predict = []
for j in range(len(test_x)):
data = test_x.values[j]
data = np.array(data)
predict.append(knn_predict(data,train_x.values,train_y.values,k))
predict = np.array(predict)
kte = 1-(test_y == predict).mean()

테스트 데이터를 이용하여 모형을 평가한 결과 에러율이 0이다. ㄷㄷ;; 지금까지는 kNN을 직접 구현해보았지만 scikit-learn에서 제공하는 KNeighborsClassifier를 이용하여 kNN 모형을 구축할 수도 있다.
## scikit learn 이용하기
from sklearn.neighbors import KNeighborsClassifier
neigh = KNeighborsClassifier(n_neighbors=opt_k)
neigh.fit(train_x.values, train_y.values)
knn_test_error = []
predict = []
for j in range(len(test_x)):
data = test_x.values[j]
data = np.array(data)
data = np.expand_dims(data, axis=0)
predict.append(neigh.predict(data))
predict = np.squeeze(predict)
kte = 1-(test_y == predict).mean()

결과는 직접 구현했던 것과 동일하다.
4. k-근접 이웃 분류기 장단점
- 장점 -
kNN은 다른 분류 모형과는 달리 학습 과정이 필요 없다. 왜냐하면 입력 데이터만 주어지면 바로 예측값을 구할 수 있기 때문이다. 그리고 kNN은 비모수 모형으로서 모형에 추가적인 가정을 하지 않으므로 가정 위배에 대한 걱정이 없다. 또한 kNN의 알고리즘은 이해하기가 쉽고 구현이 간단하다는 장점이 있으며 분류기 성능을 비교할 때 kNN의 성능과 비교하기도 한다.
- 단점 -
kNN은 다른 분류 모형과 달리 테스트 데이터의 개수에 따라 시간이 오래 걸린다는 문제가 있다. 또한 학습 데이터 모두 거리를 계산하는 데 사용하므로 학습 데이터의 양도 계산 시간에 영향을 미치게 된다.
만약 선형 모형과 같이 실제 모형을 알 수 있는 경우에는 비모수 모형보다는 모수를 이용한 모형이 더 좋을 수 있다. 그리고 변수의 개수가 많을 경우 kNN의 성능이 좋지 않다고 알려져 있다.
참고자료
Trevor Hastie외 2명 - The Elements of Statistical Learning 2nd Edition
'통계 > 머신러닝' 카테고리의 다른 글
| 6. Least Absolute Deviation Regression에 대해서 알아보자 with Python (0) | 2021.01.26 |
|---|---|
| [머신 러닝] 5. EM(Expectation-Maximization) Algorithm(알고리즘)에 대해서 알아보자. (0) | 2021.01.19 |
| [머신 러닝] 4. 나이브 베이즈 분류기(Naive Bayes Classifier) with Python (7) | 2020.12.26 |
| [머신 러닝] 3. 베이즈 분류기(Bayes Classifier) (0) | 2020.12.21 |
| [머신 러닝] 1. 소개 (0) | 2020.11.27 |





댓글