얼마전 회사에서 기초통계 강의를 했었다. 강의 주제는 가설 검정이었는데 그 중에서 P Value는 중요하다고 생각해서 여기에도 포스팅하려고 한다. 가설 검정은 일반적인 내용을 소개하고 모평균 검정, 독립 이표본 평균 비교 검정 등의 특수한 내용은 추후 따로 포스팅하겠다.
먼저 P Value를 알기 위해선 가설 검정과 그 절차를 알아야한다. 이에 대해 알아보자.
1. 가설 검정 이란?
가설 검정은 다음과 같이 정의할 수 있다.
모수에 대한 가설을 모집단으로부터 추출된 표본의 통계량을 이용하여 검정하는 일련의 과정이다.
아래 그림은 가설 검정의 예를 나타낸 것이다.

위 예를 이용하여 가설 검정 절차는 다음과 같다.
1) 만약 어느 초등학교의 3학년 수학 평균이 80점이라는 주장 또는 가설을 세웠다고 하자.
2) 여기서 모집단은 초등학교 3학년 전체가 되고 모수는 수학 평균 점수가 된다.
3) 이때 모집단을 전체 조사하는 것(비록 이 예제의 경우는 아니지만)은 시간과 비용이 많이 들기 때문에 현실적으로 힘들고 표본을 추출하여 3학년 수학 평균을 추정하게 된다.
4) 추출된 표본으로부터 통계량 즉, 3학년 수학 평균을 계산한다.
5) 4)에서 계산된 값을 이용하여 가설을 검정한다.
가설 검정은 모수(초등학교 3학년 수학 평균 점수)에 대한 가설을 모집단(초등학교 3학년)으로부터 추출된 표본(3학년 1반 학생)의 통계량(3학년 1반 학생의 수학 평균 점수)를 이용하여 가설을 검정하는 절차인 것이다.
이제 가설 검정 절차를 알아보고 가설이 참인지 거짓인지 통계적으로 판단하는 방법에 대해서 알아보자.
2. 가설 검정 절차
가설 검정 절차는 보통 다음과 같이 7단계 과정을 거친다.
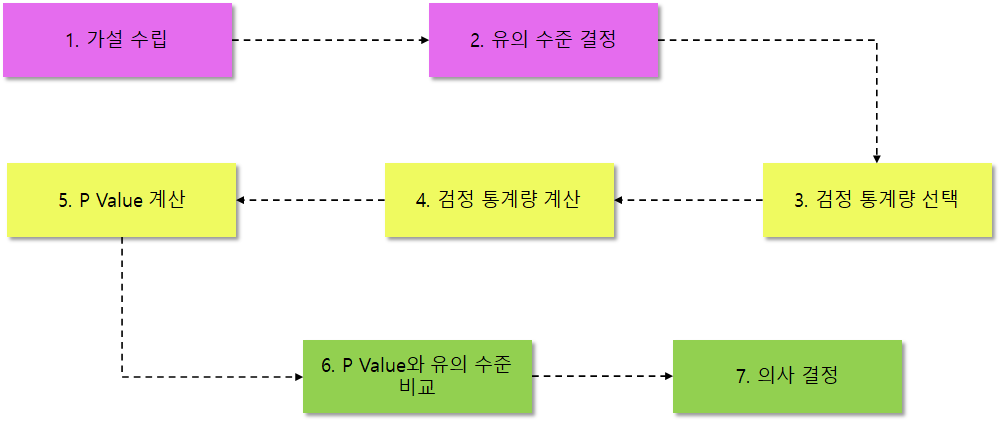
각 과정에 대해서 자세히 알아보자.
2.1 가설 수립
가설 수립 단계에서는 귀무 가설과 대립가설을 설정한다.
"귀무 가설"은 일반적으로 믿어왔던 사실을 가설로 설정하는 것으로, 영(0)가설이라고도 한다.
"대립 가설"은 귀무 가설과 대립되는 즉, 기존에 사실로 받아들여진 현상에 대립되는 가설을 의미한다.
귀무 가설은 영 가설이라는 의미에서 $H_0$로 표시하고 대립 가설은 대립을 뜻하는 "Alternative"의 앞글자를 따서 $H_a$로 표시하며 $H_1$으로 나타내기도 한다.
아래 그림은 가설 수립의 예를 나타낸 것이다.

※ 귀무 가설을 영(0) 가설이라고 하는 이유 ※
귀무 가설이 사실임을 밝히더라도
이는 일반적으로 모두가 인정하고 받아들이는 사실이기 때문에
그 파급효과가 제로(영)이기 때문
2.2 유의 수준 결정
유의 수준은 다음과 같이 정의한다.
유의 수준이란 제 1종 오류 확률의 최대 허용치이다.
유의 수준은 보통 $\alpha$로 표시한다. 유의 수준의 정의를 제대로 알려면 가설 검정에서 발생할 수 있는 오류를 먼저 알아야한다.
가설 검정도 결국 표본을 이용하여 의사결정을 하기 때문에 오류가 발생할 수 있다. 가설 검정에서 발생할 수 있는 오류는 다음과 같다.

위 표에서 보면 귀무 가설 $H_0$가 참이지만 이를 기각하는 제 1종 오류(Type I Error)와 귀무 가설 $H_0$이 거짓이지만 이를 채택하는 제 2종 오류(Type II Error)가 있다. 이를 수식으로 표현하면 다음과 같다.
제 1종 오류 = $P(H_0\text{ reject}|H_0\text{ true})$
제 2종 오류 = $P(H_0\text{ accept}|H_0\text{ false})$
전통적인 통계 가설 검정은 주로 귀무 가설을 기각하는 용도로 사용되었다. 하지만 무작정 기각하면 안될 것이다. 왜냐하면 귀무 가설이 참인 경우가 있기 때문이다. 즉, 제 1종 오류를 발생시킬 가능성이 있기 때문이다.
따라서 통계학자들은 특정 기준값을 정해두고 제 1종 오류를 범할 가능성이 어느 기준치 이상이라면 기각하지 않고 기준치 미만이라면 기각해도 좋다는 검정 시스템을 만들어 둔것이다. 이러한 기준은 제 1종 오류 확률의 최대 허용치이며 이것이 바로 유의 수준인 것이다.
2.3 검정 통계량 선택 및 계산
이 단계에서는 모집단의 대해서 가정하고 표본으로 부터 검정 통계량을 계산한다.
모집단의 대해서 가정한다는 것은 모집단의 확률 분포와 모수에 대해서 가정하겠다는 것을 의미한다(예 : 정규분포, 모분산은 알려지지 않음 등). 모집단에 대한 가정을 하는 이유는 P Value를 쉽게 계산하기 위함이다. 이러한 가정이 없다면 Bootstrap과 같은 방법을 이용하여 P Value를 구할 수 있다.
검정 통계량은 앞에서 소개할 P Value를 계산하기 위한 통계량이다.
2.4 P Value 계산
드디어 오늘의 주인공 P Value가 나왔다. P Value의 정의는 다음과 같다.
P Value란 우리가 관측한 데이터가 알려주는 (최대) 1종 오류 확률이다.
데이터가 알려준다는 것은 P Value가 데이터 표본으로 부터 계산된다는 의미이다. 이제 P Value가 왜 (최대)제 1종 오류 확률인지 알아보자. 이를 위해 모평균 단측 검정을 예로 들어서 설명하겠다. 먼저 P Value를 수식으로 표현하면 다음과 같다.
P Value = $P(H_0 \text{ reject with Data} | H_0 \text{ true})$
모분산 $\sigma^2$은 알려져있고 모평균 단측 검정에서 모평균 $\mu$가 $0$보다 작은지를 검정하고 싶다면 귀무가설과 대립가설은 다음과 같이 설정한다.
$$H_0 : \mu \geq 0 \text{ } vs \text{ } H_a : \mu < 0$$
만약 우리가 귀무 가설을 기각한다고 했을 때 제 1종 오류 확률은 얼마나 될까? 귀무 가설을 기각한다는 것은 $\mu < 0$인 경우이다. 실제로 $\mu$와 0을 비교하면 되지만 $\mu$를 알 수 없기 때문에 $\mu$의 점 추정량 $\bar{X}$와 비교를 해야한다.
귀무 가설을 기각하기 위해선 $\bar{X}$가 0보다 적당히 작으면 안될 것이고(Sampling Variance 때문에) 충분히 작아야할 것이다. 즉, $\bar{X}$가 특정값 $c$보다 작은 경우에 기각할 것이다. 이제 $\bar{X} < c$에서 귀무 가설을 기각한다고 했을 때 제 1종 오류 확률을 계산해보자.
$$\begin{align} P(H_0 \text{ reject} | H_0 \text{ true}) &= P(\bar{X} < c|\mu\geq 0) = P\left( \frac{\bar{X}-\mu}{\sigma/\sqrt{n}}<\frac{c-\mu}{\sigma/\sqrt{n}}|\mu\geq 0\right) \\ &= P\left(Z<\frac{c-\mu}{\sigma/\sqrt{n}} |\mu\geq 0 \right) \end{align}$$
세 번째 등식에서 $Z$는 표준 정규 분포를 따르는 확률 변수이다. 이때 확률값은 마지막 부등식은 $\mu=0$일 때 최대값이 된다. 즉,
$$P\left(Z<\frac{c-\mu}{\sigma/\sqrt{n}} |\mu\geq 0 \right)\leq P\left(Z<\frac{c}{\sigma /\sqrt{n}} \right)$$
위 수식을 해석하면 다음과 같다. $\bar{X} < c$에서 귀무 가설을 기각한다고 했을 때 제 1종 오류 확률의 최대값은 $P\left(Z<\frac{c}{\sigma /\sqrt{n}} \right)$라는 것이다.
이때 P Value는 $c=\bar{x}$인 경우로서 다음과 같이 계산된다.
$$P - Value = P\left( Z < \frac{\bar{x}}{\sigma/\sqrt{n}} \right)$$
이때 $\bar{x}/(\sigma/\sqrt{n})$는 검정 통계량 계산값인 것을 알 수 있다. 즉, P Value는 표본 평균값을 기준으로 기각한다고 했을 때 제 1종 오류 확률의 최대값인 것이다.
이제 P Value의 정의를 되새겨보자.
P Value는 데이터가 말해주는 (최대) 제 1종 오류 확률이다.
위키백과나 인터넷 글을 보면 P Value를 귀무 가설이 참일 때 관측값보다 더 극단값을 가질 확률로 정의하는 것을 알 수 있다. 이는 P Value의 수식을 그대로 번역한 것에 불과하며 이렇게 정의하면 언뜻 P Value와 제 1종 오류와 관계가 없어보일 수도 있다. 이것이 왜 문제냐하면 P Value와 유의 수준을 비교할 때 비교하는 이유를 모를 수 있기 때문이다. 유의 수준은 제 1종 오류 확률의 최대 허용치인데 제 1 종 오류와 관련이 없어보이는 P Value와 도대체 왜 비교하는지 모를 수 있다는 것이다.
P Value를 "데이터가 알려주는 (최대) 제 1종 오류 확률이다"라고 이해하는 것이 가설 검정 절차를 이해하는데 있어서 수월하다.
2.5 P Value와 유의수준 비교 및 의사 결정
P Value가 유의 수준 $\alpha$보다 크면 귀무 가설을 채택하고 작다면 귀무 가설을 기각한다.
P Value가 유의 수준보다 크다는 것은 우리가 허용할 수 있는 제 1종 오류 확률을 넘어섰다는 의미이며 이는 실제로 제 1종 오류를 범할 가능성이 크다는 것이다. 따라서 이러한 오류를 범하는 것을 막기 위해 귀무 가설을 기각하면 안된다는 것이다. 따라서 귀무 가설을 기각하지 않는다.
반대로 P Value가 유의 수준보다 작다는 것은 귀무 가설을 기각한다고 해도 제 1종 오류 확률의 가능성이 낮기 때문에 이는 기각해도 무방하다는 뜻이다. 즉, 귀무 가설을 기각해도 좋다는 뜻이다.
아래 그림은 P Value가 유의 수준보다 큰 경우와 작은 경우에 대한 설명을 나타낸 것이다.

이번 포스팅에서는 가설 검정과 P Value에 대해서 알아보았다. 강의 준비할 때 공부하면서 준비했는데 가설 검정 개념을 다시 한번 새길 수 있어서 좋았다. 추후에 기회가 되면 통계 검정에 대해서 포스팅하려고 한다.

'통계 > 기타' 카테고리의 다른 글
| ANOVA(Analysis of Variance, 분산분석)에 대해서 알아보자. (7) | 2022.12.06 |
|---|---|
| 통계학이란 무엇인가? (0) | 2022.11.07 |
| 가중치를 활용한 통계량을 알아보자. 가중 평균(Weighted Mean), 가중 상관계수(Weighted Correlation), 가중 분위수 (Weighted Quantile) (2) | 2022.09.25 |
| Profile Likelihood 란 무엇인가?! (408) | 2022.04.30 |
| 자유도에 대해서 정확하게 파헤쳐 보자! (2) | 2020.08.23 |





댓글