이번 포스팅에서는 데이터 간의 관계를 탐색하기 위한 방법으로 마케팅 분야에서 많이 활용되고 있는 연관 규칙 분석(마케팅에서는 장바구니 분석이라고도 한다) 대해서 알아보고자 한다.
여기서 다루는 내용은 다음과 같다.
1. 연관 규칙 분석이란 무엇인가?
- 정의 -
연관 규칙 분석(Association Rule Analysis : ARA)은 항목(item)들 관계를 If-Then 형식으로 찾아나가는 분석 방법을 말하며 일종의 규칙 기반 학습(Rule-Based Learning) 방법이다. 특히 마케팅에서는 고객들의 상품 구매 데이터를 이용하여 품목 간의 연관성을 알아본다는 의미에서 장바구니 분석(Market Basket Analysis)이라고도 한다.
- 왜 필요한가? -
연관 규칙 분석은 대용량 데이터베이스에서 기존에는 발견할 수 없었던 항목(item) 간 흥미로운 관계를 탐색할 수 있다는 장점이 있다. 아래 그림은 대형 마켓에서 고객들의 상품 구매 정보를 바탕으로 연관 규칙 분석을 수행하고 이를 활용하는 과정을 나타낸 것이다.
연관 규칙 분석을 이용하면 특정 상품을 구입한 고객이 어떤 상품을 추가로 구매하는지 알아낼 수 있다(삼겹살과 채소). 이를 통하여 효율적인 상품 진열은 무엇인지, 어떤 상품을 묶음으로 하면 좋을지를 알 수 있고 이를 통해 마케팅 전략을 수립할 수 있다.
- 응용 분야 -
위에서 소개한 마켓에서의 연관 규칙 분석을 사용하는 것외에도 호텔에서 고객들이 이용하는 서비스의 관계를 이용하여 특정 서비스를 받은 고객이 어떤 서비스를 원하는지 미리 파악하고자 할 때 연관 규칙 분석을 사용할 수 있다. 또한 웹사이트에서 고객들이 사용하는 웹 페이지간 연관관계를 이용하여 특정 웹페이지를 추천해주고 싶은 경우에도 연관 규칙 분석을 사용할 수 있다.
2. 연관 규칙 분석 방법
2.1 연관 규칙 분석 측도
먼저 어느 대형 마트의 거래 내역이 다음과 같이 주어졌다고 해보자.
| 고객 번호 | 품목 |
| 1 | 삼겹살, 상추 |
| 2 | 삼겹살, 상추, 사이다 |
| 3 | 삼겹살, 깻잎 |
| 4 | 닭고기, 샤워 타올 |
| 5 | 닭고기, 콜라, 사이다 |
이제 이 거래 내역을 이용하여 아래와 같이 구매 행렬을 만들어보자.
| 삼겹살 | 상추 | 사이다 | 깻잎 | 닭고기 | 샤워 타올 | 콜라 | |
| 삼겹살 | 3 | 2 | 1 | 1 | 0 | 0 | 0 |
| 상추 | 2 | 2 | 1 | 0 | 0 | 0 | 0 |
| 사이다 | 1 | 1 | 2 | 0 | 1 | 0 | 1 |
| 깻잎 | 1 | 0 | 0 | 1 | 0 | 0 | 0 |
| 닭고기 | 1 | 0 | 1 | 0 | 2 | 1 | 1 |
| 샤워 타올 | 0 | 0 | 0 | 0 | 1 | 1 | 0 |
| 콜라 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
위에서 만든 구매 행렬을 보면 삼겹살과 상추를 동시에 구매한 건수가 2이므로 "삼겹살을 구입하는 고객은 상추도 구입한다"라는 연관 규칙을 얻을 수 있다. 하지만 모든 연관 규칙이 유용하진 않을 것이다. 이에 따라 어떤 규칙이 유용한지를 정량적으로 측정하는 측도(지표)가 필요하다. 연관 규칙이 유용한지 알아보기 위한 여러 가지 측도를 알아보자.
1) 신뢰도(Confidence) - X를 포함하는 거래 내역 중, Y가 포함된 비율이 높아야 한다.
여기서는 비율을 확률로 표시하겠다. 이것은 "X 이면 Y이다."라고 말하려면 $P(Y | X) = P(X \cap Y)/P(X)$ 값이 높아야함을 의미한다. 다시 말해 $P(Y | X)$이 높아야 "X 이면 Y이다."라는 규칙을 신뢰할 수 있게 된다. 이러한 의미에서 $P(Y|X)$를 신뢰도라고 한다.
예를들어 "삼겹살을 사는 사람은 상추도 구입한다"라는 규칙의 신뢰도를 계산하면
$$P(\text{상추} | \text{삼겹살}) = \frac{2}{5}/\frac{3}{5} = \frac{2}{3}$$
이다.
이번엔 "삼겹살을 사는 사람은 사이다도 구입한다"라는 규칙의 신뢰도를 계산하면
$$P(\text{사이다}|\text{삼겹살}) = \frac{1}{5}/\frac{3}{5} = \frac{1}{3}$$
이다. 따라서 신뢰도가 더 높은 "삼겹살을 사는 사람은 상추도 구입한다"는 규칙이 "삼겹살을 사는 사람은 사이다도 구입한다"라는 규칙보다 더 신뢰하겠다는 것이다. 어찌 보면 당연하다.
2) 지지도(Support) - X와 Y를 동시에 포함하는 비율이 높아야 한다.
"상추를 구입하는 사람은 사이다도 구입한다"라는 규칙의 신뢰도를 계산해보자.
$$P(\text{사이다}|\text{상추}) = \frac{1}{5}/\frac{2}{5}=\frac{1}{2}$$
즉, "상추를 구입하는 사람은 사이다도 구입한다"라는 규칙이 "삼겹살을 사는 사람은 상추도 구입한다"는 규칙보다 더 신뢰한다는 말이 된다. 하지만 사이다와 상추를 동시에 포함하는 거래 건수는 5개 중 1개뿐이다. 따라서 "상추를 구입하는 사람은 사이다도 구입한다"한다는 규칙은 아직 지지받기에는 발생 횟수가 충분하지 않다. 즉, "X이면 Y이다."라는 규칙이 지지받기 위해서는 실제로 $X, Y$를 동시에 포함하는 비율 $P(X \cap Y)$이 높아야 된다는 것이다. 이러한 의미에서 $P(X \cap Y)$를 지지도라고 한다.
예를 들어 "삼겹살을 사는 사람은 상추도 구입한다"라는 규칙의 지지도는 다음과 같다.
$$P(\text{삼겹살}, \text{상추}) = \frac{2}{5} $$
따라서 "삼겹살을 사는 사람은 상추도 구입한다"라는 규칙의 지지도가 "상추를 구입하는 사람은 사이다도 구입한다"라는 규칙의 지지도보다 높다.
3) 향상도(Lift) - 지지도와 신뢰도만으로 충분한가?
만약 $X \Rightarrow Y$라는 규칙이 있다고 하자. 그렇다면 실제로 $X$는 $Y$라는 사건을 설명하기에 의미 있는 사건 또는 변수라고 할 수 있을까? 아닐 것이다. 예를 들어 신뢰도를 계산했더니 $P(Y|X)=0.9$가 나왔다. 0.9 정도면 높다고 생각하여 $X \Rightarrow Y$라는 규칙이 의미 있다고 생각할 것이다. 하지만 $Y$가 발생한 비율이 $p(Y)=0.9$였다고 생각해보자. 그렇다면 $P(Y | X) = P(Y)$가 된다. 즉, $X$와 $Y$는 독립이 되어 $X$는 $Y$를 설명하는데 아무런 도움을 주지 못한다. 따라서 주어진 규칙이 진짜로 의미가 있는지 알아보기 위하여 $P(Y|X)/P(Y)$를 계산하게 되는데 향상도(Lift)라 한다.
향상도의 값이 1이면 $X$와 $Y$는 아무런 관계가 없게 된다. 만약 1보다 크다면 $X$가 $Y$의 발생할 확률을 $X$를 고려하지 않을 경우보다 증가시킨다는 뜻이며 이는 $X$가 $Y$의 발생을 예측하는데 좋다고 할 수 있다. 반대로 1 보다 작으면 $X$가 $Y$의 발생 확률을 $X$를 고려하지 않았을 경우보다 감소시킨다는 뜻이 된다. 이는 $X$가 $Y$의 발생 감소를 예측하는데 좋다고 할 수 있으며 $X$와 $Y$가 일종의 음의 상관관계를 나타낸다고 할 수 있다.
"삼겹살을 사는 사람은 상추도 구입한다"라는 규칙의 향상도를 구해보자.
$$ P(\text{상추}|\text{삼겹살})/P(\text{상추}) = \frac{2}{3}/\frac{2}{5} = \frac{5}{3}$$
4) 레버리지(Leverage) - 향상도(Lift)는 비율을 이용한다면 레버리지(Leverage)는 차이를 이용한다!
향상도는 $X$ 와 $Y$의 독립 여부를 판단하기 위하여 $P(Y|X) / P(Y)$를 이용했다면 레버리지는 $P(X\cap Y)- P(X)P(Y)$를 계산한다. 따라서 레버리지가 0에 가깝다면 $X$와 $Y$는 독립, 즉 $X$와 $Y$는 상호 연관성이 없다고 할 수 있으며 레버리지가 양수라면 향상도가 1보다 큰 경우와 같으며 레버리지가 음수이면 향상도가 1보다 작은 경우와 같다.
"삼겹살을 사는 사람은 상추도 구입한다"라는 규칙의 레버리지를 구해보자.
$$P(\text{삼겹살}, \text{상추}) - P(\text{삼겹살})P(\text{상추}) = \frac{2}{5}-\frac{3}{5}\frac{2}{5} = \frac{4}{25} $$
결국 향상도와 레버리지는 같은 역할을 하는데 굳이 레버리지라는 측도를 도입한 이유는 무엇일까? 곰곰이 생각해보았다. 아마도 향상도는 비율이기 때문에 계산의 불안정성(분모가 0에 가까운 아주 작은 수일 때)이 있기 때문에 계산상으로 안정적인 레버리지를 고려하는 것이라 생각했다. 물론 레버리지가 아주 작다고(0.01-0.005=0.005)해도 향상도(0.01/0.005=2)는 비율이기 때문에 커질 수 있다. 다시 말하면 레버리지가 작아서 $X$, $Y$의 관계를 제대로 알 수 없었지만 향상도를 이용하면 그 관계를 좀 더 분명하게 알아낼 수다는 장점이 있어서 향상도 또한 중요하다.
5) Conviction - 어떤 일이 생길 것에 관심을 갖는 것처럼 어떤 일이 생기지 않는 것에도 관심을 가져보자!
규칙 $X\Rightarrow Y$의 Conviction은 $P(Y^c)/P(Y^c|X)$로 정의한다. Conviction 값이 1이면 $X, Y$는 상호 연관성이 없는 즉, 독립을 의미한다. Conviction이 1보다 크다면 $X$가 주어졌을 경우 $Y$가 발생하지 않는 경우가 $X$를 고려하지 않았을 경우보다 줄어들었다는 것을 의미한다. 반대로 말하면 $X$가 $Y$의 발생 여부를 예측하는데 유용한 품목이 되는 것이다. 비슷한 논리로 Conviction이 1보다 작으면 $X$는 $Y$의 발생 여부를 예측하는데 유용하지 않은 품목이 되는 것이다.
"삼겹살을 사는 사람은 상추도 구입한다"라는 규칙의 Conviction을 구해보자.
$$ P(\text{상추}^c)/P(\text{상추}^c|\text{삼겹살}) = P(\text{상추}^c)/[1-P(\text{상추}|\text{삼겹살})] =\frac{3}{5}/(1-\frac{2}{3}) = \frac{9}{5}$$
6) All-Confidence - 높은 지지도를 갖는 규칙을 고려하자~!!
All-Confidence는 Omiecinski의 2003년 논문 "Alternative Interest Measures for Mining Associations in Databases"에서 소개한 측도이며 품목 집합(item set) $(X, Y)$의 All-Confidence는 다음과 같이 정의한다.
$$\text{All-Confidence}(X, Y) = P(X \cap Y)/\max [P(X), P(Y)]$$
All-Confidence는 $X$와 $Y$의 지지도 중 높은 것을 선택하여 만들어진 규칙을 고려하겠다는 것이다.
또한 특정 품목 집합의 All-Confidence이 특정 값 $c$보다 크다면 그 집합의 부분 집합으로 이루어진 All-Confidence 또한 $c$보다 크다는 성질인 Downward Closure Property(DCP)를 만족한다. DCP는 의미 있는 규칙을 뽑아낼 때 필요한 품목 조합 연산을 크게 줄여줄 수 있다.
품목 집합 '삼겹살, 상추'의 All-Confidence를 구해보자.
$$\begin{align} \text{All-Confidence}(\text{삼겹살}, \text{상추}) &= P(\text{삼겹살}, \text{상추})/\max [P(\text{삼겹살}), P(\text{상추})] \\ &= P(\text{삼겹살}, \text{상추})/P(\text{삼겹살}) \\ &= \frac{2}{5}/\frac{3}{5} \\ &= \frac{2}{3} \end{align}$$
따라서 "상추$\Rightarrow$삼겹살"과 "삼겹살$\Rightarrow$상추" 중에서 "삼겹살 $\Rightarrow$상추"를 고려한다.
7) Collective Strength - 지지도와 신뢰도를 믿을 수 없다! 새로운 측도가 필요하다~!!
Aggarwal는 1998년 논문 "Mining Associations with the Collective Strength Approach"에서 지지도와 신뢰도를 잘못 설정할 경우 "$X \Rightarrow Y$"와 "$X \Rightarrow \neg Y$"를 동시에 뽑아내는 모순적인 결과를 얻을 수 있다는 점을 지적하면서 Collective Strength라는 개념을 도입했다. 품목 집합 $X, Y$의 Collective Strength $CS(X,Y)$는 다음과 같이 정의한다.
$$CS(X, Y) = \frac{1-V(X,Y)}{1-E(V(X, Y))}\frac{E(V(X,Y))}{1-V(X,Y)}$$
여기서 $V(X, Y) = P(X\cap Y^c)+P(X^c \cap Y)$이고 $E(V(X, Y))$는 $V(X, Y)$의 기대값을 $X$와 $Y$의 독립을 가정하여 얻은 값으로 다음과 같다.
$$E(V(X,Y)) = 1-P(X)P(Y)-[1-P(X)][1-P(Y)]$$
참고로 $V(X,Y)$를 Violation이라 한다.
C(X, Y)는 0부터 무한대의 값을 가질 수 있으며 1인 경우 $X, Y$는 독립이라고 가정한다. 만약 1보다 작은 경우 어느 한 품목의 발생이 다른 품목의 발생 가능성을 낮추는 일종의 음의 상관관계가 존재한다고 해석할 수 있으며 0인 경우 완벽한 음의 상관관계가 존재한다고 볼 수 있다. 만약 1보다 큰 경우 어느 한 품목의 발생이 다른 품목의 발생 가능성을 높이는 양의 상관관계가 존재하며 무한대인 경우 완벽한 양의 상관관계가 존재한다고 해석할 수 있다.
품목 집합 '삼겹살, 상추'의 Collective Strength를 구해보자.
$$V(\text{삼겹살}, \text{상추}) = \frac{1}{5}+0 = \frac{1}{5} \\ E(V(\text{삼겹살}, \text{상추})) = 1-\frac{3}{5}\cdot\frac{2}{5}-\frac{2}{5}\cdot\frac{3}{5} = \frac{13}{25}$$
따라서
$$CS(\text{삼겹살}, \text{상추}) = \frac{1-\frac{1}{5}}{1-\frac{13}{25}}\frac{\frac{13}{25}}{\frac{1}{5}} = \frac{13}{3}$$
'삼겹살, 상추'의 Collective Strength가 1보다 크므로 삼겹살과 상추는 양의 상관관계를 갖는 연관 규칙이라 할 수 있다.
8) Cosine Similarity - 나도 끼워줘!!
품목 집합 $X, Y$의 Cosine Similarity는 다음과 같이 정의한다.
$$\cos (X,Y) = \frac{P(X, Y)}{\sqrt{P(X)\sqrt{P(Y)}}}$$
Cosine Similarity는 0부터 1의 값을 가지며 0인 경우는 완벽한 음의 상관관계, 1인 경우는 완벽한 양의 상관관계를 의미한다.
'삼겹살, 상추'의 Collective Strength를 구해보자.
$$\begin{align}\cos (\text{삼겹살}, \text{상추}) &= P(\text{삼겹살}, \text{상추})/\left [\sqrt{P(\text{삼겹살})}\sqrt{P(\text{상추})}\right ] \\ &= \frac{2}{5}/\left [\sqrt{\frac{3}{5}}\sqrt{\frac{2}{5}} \right ] = 0.82 \end{align}$$
2.2 연관 규칙 분석 절차
품목이 많아질수록 예를 들어 $p$개이면 고려해야 할 품목 집합수는 $2^p-2$(공집합과 전체집합 제외)이므로 $p$가 커진다면 모든 품목 집합을 고려하는 것은 현실적으로 불가능하다. 이번 포스팅에서는 최소 지지도, 최소 신뢰도를 갖는 연관 규칙을 찾는 대표적인 방법으로 Apriori 알고리즘을 소개한다. 내용
Apriori 알고리즘은 2단계로 이루어진다.
1. 빈발 품목 집합(Frequent Item Set) 생성
2. 연관 규칙 생성
2.2.1 빈발 품목 집합(Frequent Item Set) 생성
빈발 품목 집합(Freqeunt Item Set)은 각 품목별로 발생 횟수(비율)가 특정 값 이상인 품목을 모아놓은 집합을 말한다. Apriori 알고리즘은 다음과 같이 빈발 품목 집합을 찾는다.
1) 최소 지지도(최소 발생 비율)를 설정한다.
$p = 1, 2, 3, \cdots$에 대하여
2) $p$개의 품목을 갖는 품목 집합 중에서 최소 지지도를 넘는 품목을 찾는다.
3) 위에서 찾은 품목 중에서 최소 지지도를 넘는 $p+1$개 품목 집합을 찾는다.
위 과정을 반복하면 최소 지지도가 넘는 빈발 품목 집합을 찾을 수 있다. 1)에서 최소 지지도를 설정해야 하는데 설정하는 절대적인 방법은 없으며 순전히 분석자의 몫이다.
2.2.2 연관 규칙 생성
빈발 품목 집합의 공집합을 제외한 모든 부분집합을 고려하고 이 중에서 최소 신뢰도를 넘는 연관 규칙을 찾는다.
3. 고려 사항
- 유용한 연관 규칙 선별 -
연관 규칙 분석으로부터 찾은 모든 연관 규칙(또는 연관성)이 유용하지는 않을 것이다. 왜냐하면 이러한 규칙들은 유용한 규칙, 너무 뻔한 규칙, 연관성을 찾기 힘든 규칙이 있기 때문이다. 예를 들어 "토요일에 대형 마켓을 찾는 남성은 아기 기저귀와 함께 맥주를 같이 사는 경향이 있다"는 규칙(정보)는 마케팅 전략에 직접적으로 사용될 수 있기 때문에 유용한 정보라 할 수 있다. 반면, "아이폰을 사는 고객은 아이폰을 사는 경향이 있다."는 정보는 어찌 보면 뻔한 것이기 때문에 가치있는 규칙이라 할 수 없다. 마지막으로 "식료품을 파는 곳에서 선풍기가 많이 팔린다."는 규칙은 연관성을 찾기 힘들 것이다. 연관 규칙 분석을 통하여 얻어진 규칙들 중에서 어떤 규칙이 유용한지는 분석자의 판단에 달려있다.
-적절한 품목 선택-
어떤 품목을 선택하는가는 분석 목적에 달려있다. 품목을 소주, 맥주, 막걸리 등으로 세분화할 수도 있으며 소주, 맥주, 막걸리를 하나의 상위 개념인 술로 묶을 수도 있을 것이다. 일반적으로 상위 개념을 품목으로 정하여 연관 규칙을 찾은 후, 이를 세분화하여 추가적으로 연관 규칙 분석을 수행한다. 예를 들어 술과 양식이라는 상위 카테고리로 규칙을 찾았다면 술을 맥주, 소주, 막걸리 등으로 세분화하고 양식도 피자, 햄버거, 치킨 등으로 세분화한 뒤 연관 규칙 분석을 수행하는 것이 일반적이다.
-연관 규칙 발굴-
연관 규칙을 선택할 때 어떻게 표현되어있는지도 중요하다. 예를들어 "목요일에 기저귀를 사는 사람은 맥주도 산다"라는 규칙이 "목요일에 방문하는 고객은 기저귀와 맥주를 산다"에 비해 조건은 보다 구체적이고 결과는 더 단순하므로 해석이 쉽고 의미 있는 규칙이 될 수 있다. 즉, 가정은 구체적이고 결과는 단순한 것이 좋을 수 있다. 또한 향상도가 1보다 작은 경우는 결과를 부정하여 새롭게 만들어낸 규칙이 의미가 있을 수도 있다. 예를 들어 "아이스크림을 사는 사람은 40대 이상이다"라는 규칙의 향상도가 1보다 작다면 "아이스크림을 사는 사람은 40대 미만이다"라는 규칙을 점검해보자는 뜻이다.
-계산 문제-
품목의 수가 증가하면 계산량은 엄청나게(exponential 하게) 증가하며 연관 규칙을 찾아내는데 엄청난 시간이 소요된다. 이러한 문제점 때문에 최소 지지도보다 작은 규칙들은 선택하지 않는 가지치기(minimum support pruning)를 적용한다.
4. 예제 with Python
먼저 데이터를 다운 받아준다.
필요한 모듈을 임포트하고 데이터를 불러온다.
import matplotlib.pyplot as plt
import matplotlib.colors as mcl
import pandas as pd
import numpy as np
from matplotlib.colors import LinearSegmentedColormap
from mlxtend.preprocessing import TransactionEncoder
from mlxtend.frequent_patterns import apriori, association_rulesstore_df = pd.read_csv('../dataset/store_data.csv', header=None)
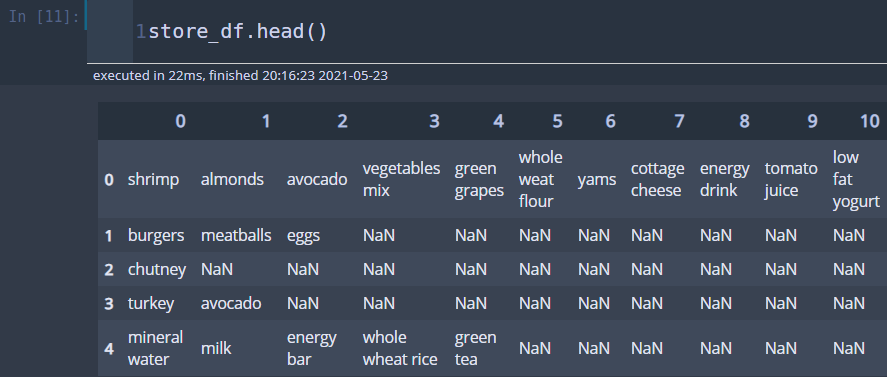
Python에서는 mlxtend 라이브러리를 이용하여 연관 규칙 분석을 수행할 수 있다. 먼저 빈발 품목 집합을 구해보자. 우선 각 행에 대해서 품목을 리스트로 만들어주고 이를 다시 리스트로 모아줘야 한다. 즉, 리스트의 리스트를 만들어줘야 한다.
records = []
for i in range(len(store_df)):
records.append([str(store_df.values[i,j]) \
for j in range(len(store_df.columns)) if not pd.isna(store_df.values[i,j])])
다음으로 mlxtend를 사용하기 위한 데이터프레임을 만들어준다. 이 데이터프레임은 각 행별로 품목이 포함되어 있으면 1 아니면 0으로 되어있다.
te = TransactionEncoder()
te_ary = te.fit(records).transform(records, sparse=True)
te_df = pd.DataFrame.sparse.from_spmatrix(te_ary, columns=te.columns_)
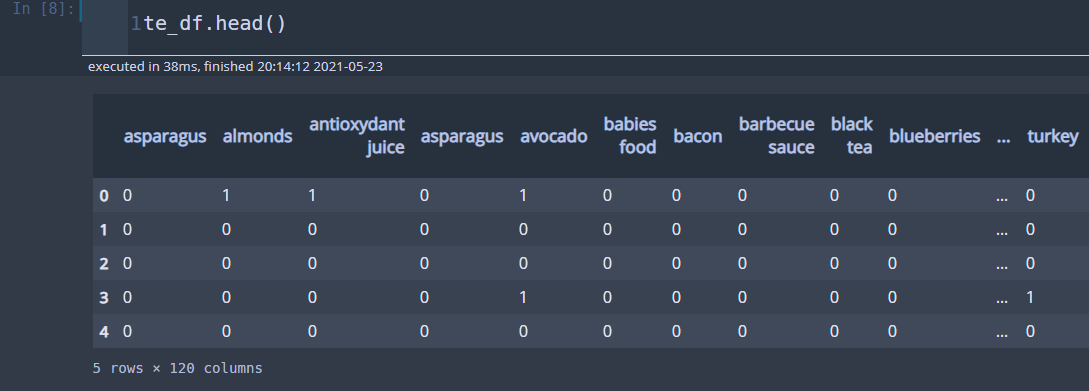
이제 빈발 품목 집합을 만들어보자. 최소 지지도는 0.005, 품목 집합 최대 개수는 3개로 설정했다. use_columns를 True로 설정하면 품목 집합을 칼럼 이름으로 지정한다. 그리고 진행 상황을 보기 위해 verbose=1로 지정했다(하지만 프로그레스 바는 나오지 않는다). 그리고 length라는 칼럼을 만들어 품목 집합 개수를 나타냈고 지지도를 기준으로 내림차순 하였다.
frequent_itemset = apriori(te_df,
min_support=0.005,
max_len=3,
use_colnames=True,
verbose=1
)
frequent_itemset['length'] = frequent_itemset['itemsets'].map(lambda x: len(x))
frequent_itemset.sort_values('support',ascending=False,inplace=True)
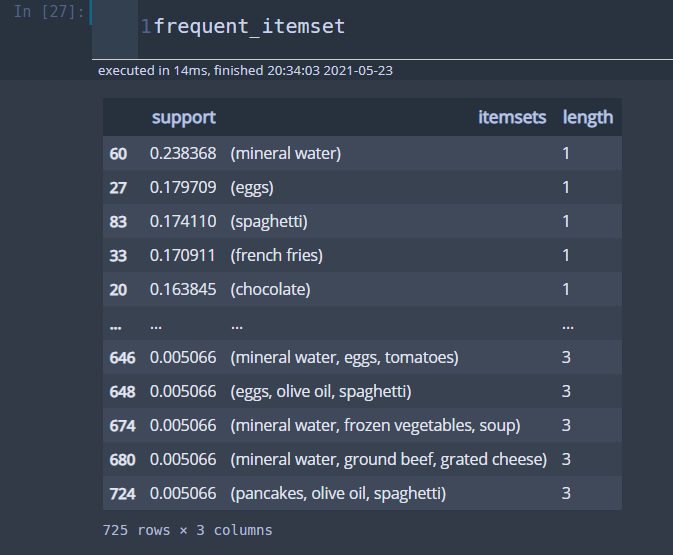
다음 코드는 연관 규칙을 뽑아내는 코드이다. 신뢰도가 0.005 이상인 연관 규칙만 뽑아낸다. 또한 앞에서 소개한 여러 가지 측도를 계산하여 칼럼으로 추가하였다.
association_rules_df = association_rules(frequent_itemset,
metric='confidence',
min_threshold=0.005,
)
all_confidences = []
collective_strengths = []
cosine_similarities = []
for _,row in association_rules_df.iterrows():
all_confidence_if = list(row['antecedents'])[0]
all_confidence_then = list(row['consequents'])[0]
if row['antecedent support'] <= row['consequent support']:
all_confidence_if = list(row['consequents'])[0]
all_confidence_then = list(row['antecedents'])[0]
all_confidence = {all_confidence_if+' => '+all_confidence_then : \
row['support']/max(row['antecedent support'], row['consequent support'])}
all_confidences.append(all_confidence)
violation = row['antecedent support'] + row['consequent support'] - 2*row['support']
ex_violation = 1-row['antecedent support']*row['consequent support'] - \
(1-row['antecedent support'])*(1-row['consequent support'])
collective_strength = (1-violation)/(1-ex_violation)*(ex_violation/violation)
collective_strengths.append(collective_strength)
cosine_similarity = row['support']/np.sqrt(row['antecedent support']*row['consequent support'])
cosine_similarities.append(cosine_similarity)
association_rules_df['all-confidence'] = all_confidences
association_rules_df['collective strength'] = collective_strengths
association_rules_df['cosine similarity'] = cosine_similarities
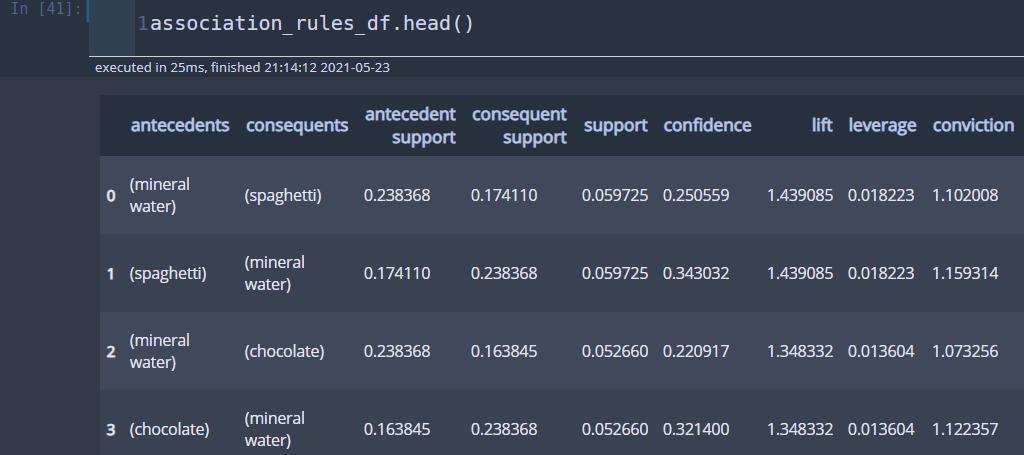
결과를 5행만 출력해보자.
max_i = 4
for i, row in association_rules_df.iterrows():
print("Rule: " + list(row['antecedents'])[0] + " => " + list(row['consequents'])[0])
print("Support: " + str(round(row['support'],2)))
print("Confidence: " + str(round(row['confidence'],2)))
print("Lift: " + str(round(row['lift'],2)))
print("=====================================")
if i==max_i:
break
첫 행을 보면 'mineral water'를 사는 고객은 'spaghetti'를 산다는 규칙은 지지도가 0.06, 신뢰도가 0.25 그리고 향상도는 1.44라는 것을 알 수 있다. 향상도가 1보다 크므로 'mineral water'와 'spaghetti'는 일종의 양의 상관관계가 있다고 해석할 수 있다.
아래 코드는 연관 규칙 분석 결과를 시각화하는 방법이다. 지지도를 x축으로 신뢰도를 y축으로 하고 컬러 맵은 각 측도를 이용하여 표현하였다.
support = association_rules_df['support']
confidence = association_rules_df['confidence']
h = 347
s = 1
v = 1
colors = [
mcl.hsv_to_rgb((h/360, 0.2, v)),
mcl.hsv_to_rgb((h/360, 0.55, v)),
mcl.hsv_to_rgb((h/360, 1, v))
]
cmap = LinearSegmentedColormap.from_list('my_cmap',colors,gamma=2)
measures = ['lift', 'leverage', 'conviction',
'all-confidence', 'collective strength', 'cosine similarity']
fig = plt.figure(figsize=(15,10))
fig.set_facecolor('white')
for i, measure in enumerate(measures):
ax = fig.add_subplot(320+i+1)
if measure != 'all-confidence':
scatter = ax.scatter(support,confidence,c=association_rules_df[measure],cmap=cmap)
else:
scatter = ax.scatter(support,confidence,c=association_rules_df['all-confidence'].map(lambda x: [v for k,v in x.items()][0]),cmap=cmap)
ax.set_xlabel('support')
ax.set_ylabel('confidence')
ax.set_title(measure)
fig.colorbar(scatter,ax=ax)
fig.subplots_adjust(wspace=0.2, hspace=0.5)
plt.show()
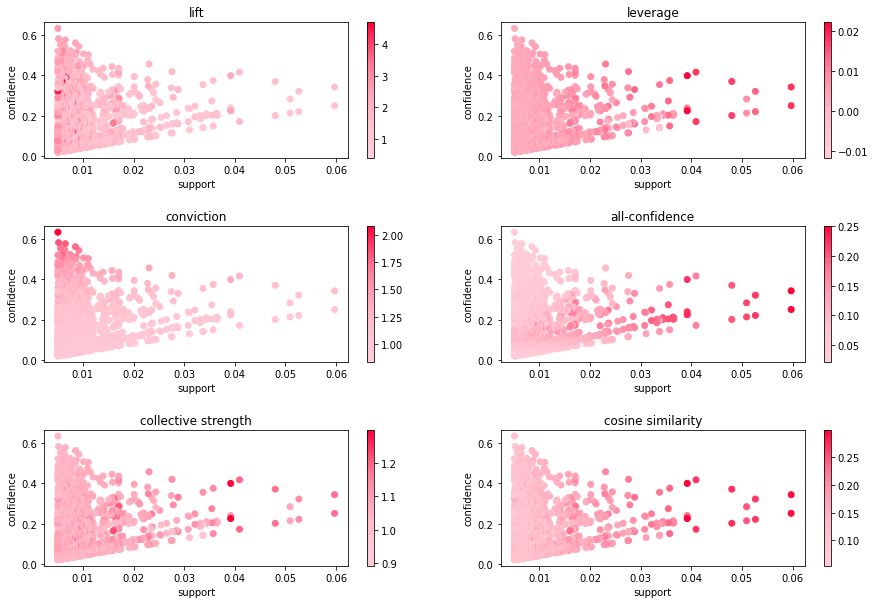
이제 분석 목적에 맞게 본인이 원하는 연관 규칙을 최종적으로 선택하면 되는데 분석자의 주관 또는 도메인 전문가와 상의하여 고르는 방법 외에는 특별한 방법은 없는 것 같다.
참고자료
Association Rule Mining via Apriori Algorithm in Python - https://stackabuse.com/association-rule-mining-via-apriori-algorithm-in-python/
김용대 외 3명 - R을 이용한 데이터마이닝
Association Pattern Mining - https://cs.nju.edu.cn/zlj/Course/DM_16_Lecture/Lecture_4.pdf
Aggarwal(1998) - Mining Associations with the Collective Strength Approach
Omiecinski(2003) - Alternative Interest Measures for Mining Associations in Databases
'통계 > 머신러닝' 카테고리의 다른 글
| 10. 가지치기(Pruning)에 대해서 알아보자 with Python (1267) | 2021.07.05 |
|---|---|
| 9. 의사결정나무(Decision Tree) 에 대해서 알아보자 with Python (1275) | 2021.06.10 |
| [Quantile Regression] 2. Quantile regression : Understanding how and why? (1557) | 2021.05.05 |
| [Quantile Regression] 1. A visual introduction to quantile regression (1085) | 2021.04.24 |
| 7. 이상치 탐지(Outlier Detection) - 통계적 검정과 여러가지 판별법 with Python (2) | 2021.02.17 |
댓글