본 포스팅에서는 수식을 포함하고 있습니다.
티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니
PC 웹 브라우저 또는 모바일 웹 브라우저에서 보시기 바랍니다.
이번 포스팅에서는 각종 기대값의 근사치를 구하거나 순서 통계량의 누적 분포를 구할 때 필요한 Gaussian Quadrature 적분 관련 논문인 Steen 외 2명의 논문 'Gaussian Quadratures for the Integrals'을 소개하고 여기에서 제시한 적분 근사 방법을 파이썬으로 구현해보고자 한다.
여기서 다루는 내용은 다음과 같다.
2. Computation of Weights and Abscissae
Abstract
Gaussian-Hermite Quadrature 적분은 아래와 같이 $(-\infty, \infty)$에서의 적분을 특정 지점에서의 함수값과 가중치의 합으로 근사하는 방법이다.
$$\int_{-\infty}^{\infty}\exp (-x^2)f(x)dx \approx \sum_{i=1}^nw_if(x_i)$$
하지만 구간 $(-\infty,\infty)$ 뿐 아니라 $(0,\infty)$ 또는 $(0, b), \;b<\infty$와 같은 구간에서의 적분도 많이 활용된다. 따라서 본 논문에서는 마지막 2개의 구간에 대해서 적분값을 근사하는 방법에 대해서 소개한다. 여기서 $w_i$ 는 가중치(weight), $x_i$는 가로 좌표점(abscissa)이라 하는데 가로 좌표점의 경우에는 특정 포인트 혹은 특정 지점으로 용어를 바꿔 사용하겠다.
본 논문에서는 $(0,\infty)$와 $(0, 1)$에 대해서 $2\leq n \leq 15$에서의 가중치와 특정 지점을 계산하였으며 각각의 값은 15자리의 유효숫자로 표시하였다.
1. Introduction
아래와 같은 적분 계산은 여러 분야에서 활용된다.
$$\int_0^b\exp (-x^2) f(x) dx \tag{1}$$
또는
$$\int_0^{\infty}\exp (-x^2) f(x) dx \tag{2}$$
$f(x)$가 다항함수와 같이 쉬운 함수라면 위의 적분은 Analytical 하게 구할 수 있으므로 문제가 되지 않지만 $f(x)$가 $x<0$에서 정의되지 않은 상황에서 복잡한 함수라면 적분을 직접 계산하는 것보다는 근사를 통해 계산하는 것도 고려해볼 만하다. 따라서 본 논문에서는 (1), (2)의 적분을 근사하는 방법을 소개한다.
기존의 Gauss-Laguerre quadrature 적분 근사는 $u=x^2$와 같은 변환이 필요한데 이 경우에는 원점에서 Singular 한 문제가 발생하여 구할 수 없다. 또 다른 잘 알려진 방법으로 Gauss-Hermite quadrature 적분 근사가 있는데 이 경우 $f$에 대한 even extension을 이용하여 구할 수도 있다. $g$를 $f$에 대한 even extension이라고 하자. $g$가 원점에서 높은 차수의 미분이 되지 않는다면 다시 말해 충분히 smooth하지 않다면 (2)에 대한 근사값이 $n$이 증가함에 따라 진동한다고 한다. 저자는 $f(x) = x^k, \;\;k=1, 3$에 대해서 Gauss-Hermite Quadrature 적분 근사 값과 직접 적분한 값과의 상대적 차이를 비교해보았다. 그 결과는 아래 Table 1에서 볼 수 있다. 실제로 높은 차수의 미분이 되지 않는 경우($k=1$) 상대적 오차가 굉장히 크고 $n$이 증가함에 따라 부호가 바뀌는 것을 볼 수 있다.

만약 $f$가 even이라면 기존의 Gauss-Hermite quadrature 적분 근사 방법이 본 논문에서 제시한 방법보다 더 좋을 수 있다고 한다. 왜냐하면 $\exp (-x^2)f(x)$가 원점에 대하여 대칭이 되므로 한쪽 방향의 특정 지점만 구하면 되기 때문이다. 즉, 기존에 필요한 특정 지점 개수보다 절반만 있으면 되기 때문에 계산이 빨라진다.
2. Computation of Weights and Abscissae
먼저 $\gamma_N$을 다음과 같이 정의한다.
$$\gamma_N = \int_0^b\exp (-x^2)p_N(x)^2dx$$
여기서 $p_N(x)$는 다음과 같이 재귀적으로 정의된다.
$$\begin{align}p_0(x) &= 1 \\ p_1(x) &= x-[1-\exp (-b^2)]/(\sqrt{\pi}\text{erf} (b)) \\ p_{k+1}(x) &= (x+\alpha_k)p_k(x) + \beta_kp_{k-1}(x)\;\; k=1, 2, \ldots \end{align}$$
이때 $\alpha_k$, $\beta_k$는 다음과 같이 정의된 상수이다.
$$\alpha_k = -\gamma_k^{-1}\int_0^b \exp (-x^2)xp_k(x)^2dx, \; \beta_k = -\gamma_k/\gamma_{k-1}$$
이제 가중치 $w_j$와 특정 지점 $x_j$을 구하자. $x_j, j=1, \ldots, n$은 $p_n(x)$의 $n$개 근이며 가중치는 다음과 같이 구한다.
$$w_j = \frac{\gamma_n}{(p_n'(x_j))p_{n-1}(x_j)}$$
이렇게 가중치와 특정 지점을 구했다면 (1)은 다음과 같이 근사할 수 있다.
$$\int_0^b\exp (-x^2)f(x)dx \approx \sum_{i=1}^nw_if(x_i)$$
여기서는 $(0, b)$ 위에서의 적분이지만 앞의 결과에서 $b\rightarrow \infty$로 하고 가중치와 다항식 그리고 특정 지점을 구해준다면 $(0, \infty)$에서의 적분 근사도 할 수 있다.
이 이후에는 Orthogonality를 이용하여 계산을 좀 더 쉽게 할 수 있는 방법이 나온다.
3. Implementation with Python
이제 파이썬을 이용하여 $n$이 주어졌을 때 가중치와 특정 지점을 계산하는 함수를 만들 것이다.
필요한 모듈을 먼저 임포트한다.
import numpy as np
from scipy.special import erf
다음으로 다음의 적분값을 계산하는 함수를 구한다.
$$\int_0^b \exp(-x^2)x^kdx, \;\; k=0, 1, \ldots $$
def get_exp_xpower_int(k, b=None):
'''
if b == None, b == infty
'''
if b:
if k==0:
return (np.sqrt(np.pi)/2)*erf(b)
elif k==1:
return 0.5*(1-np.exp(-np.square(b)))
else:
return ((k-1)*0.5)*get_exp_xpower_int(k-2,b)-0.5*np.power(b,k-1)*np.exp(-np.square(b))
else:
if k==0:
return np.sqrt(np.pi)/2
elif k==1:
return 1/2
else:
return ((k-1)*0.5)*get_exp_xpower_int(k-2)
다음으로 다항식 $p(x) = a_0 + a_1x + \cdots + a_nx^n$에 대하여 다음의 적분값을 계산하는 함수를 정의한다.
$$\int_0^b \exp(-x^2)p(x)dx$$
def get_exp_poly_int(coef,b=None):
res = 0
for i in range(len(coef)):
res += coef[i]*get_exp_xpower_int(i,b)
return res
다음으로 Orthogonal 다항식 $p_n(x)$의 계수를 계산해주는 함수를 정의한다.
def get_polynomial(n,b=None):
if n == 0:
return np.array([1])
elif n == 1:
if b:
return np.array([1, -(1-np.exp(-np.square(b)))/(np.sqrt(np.pi)*erf(b))])
else:
return np.array([1, -(1/np.sqrt(np.pi))])
else:
first = get_polynomial(n-1,b)
## calculate gamma
p = np.poly1d(first)
p2 = p*p ## square polynomial
p2_coef = np.flip(p2.coef) ## reverse coefficient
gamma_first = get_exp_poly_int(p2_coef,b) ## gamma[n-1]
p2_coef_shifted = np.insert(p2_coef,0,0) ## x*polynomial
integral_component = get_exp_poly_int(p2_coef_shifted,b)
alpha = -((1/gamma_first))*integral_component
first_plus_order = np.insert(first, len(first), 0) ## x*p(x)
first_plus_order = np.poly1d(first_plus_order)
first_multiplied_const = alpha*first ## alpha*p(x)
first_multiplied_const = np.poly1d(first_multiplied_const)
second = get_polynomial(n-2,b) ## second term
ps = np.poly1d(second)
ps2 = ps*ps
ps2_coef = np.flip(ps2.coef)
gamma_second = get_exp_poly_int(ps2_coef,b)
beta = -gamma_first/gamma_second
second_multiplied_const = beta*second
second_multiplied_const = np.poly1d(second_multiplied_const)
return (first_plus_order+first_multiplied_const+second_multiplied_const).coef
이제 마지막으로 가중치와 특정 지점을 계산하는 함수를 정의한다.
def get_weight_and_poins(n,b=None):
assert n > 0 and isinstance(n,int), 'n must be integer greater than 0'
coef = get_polynomial(n,b)
coef_prev = get_polynomial(n-1,b)
points = np.roots(coef)
p = np.poly1d(coef)
p_prev = np.poly1d(coef_prev)
p2_prev = p_prev*p_prev
p2_prev_coef = np.flip(p2_prev.coef)
gamma = get_exp_poly_int(p2_prev_coef,b)
first = p.deriv()(points)
second = p_prev(points)
denominator = first * second
weights = gamma/denominator
weights
return (weights, points)
이제 실험을 해보자. 먼저 $n=3$인 경우 $(0, \infty)$에서의 적분을 근사하기 위한 가중치와 특정 지점을 구해보자.
get_weight_and_poins(3)

결과를 논문의 결과와 비교해보자.
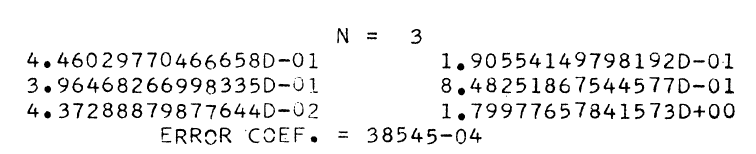
정확하게 똑같이 나왔다. 또한 $n$이 4~10인 경우에도 정확하게 일치하였다. 이번엔 $n=15$인 경우를 구해보자.
get_weight_and_poins(15)

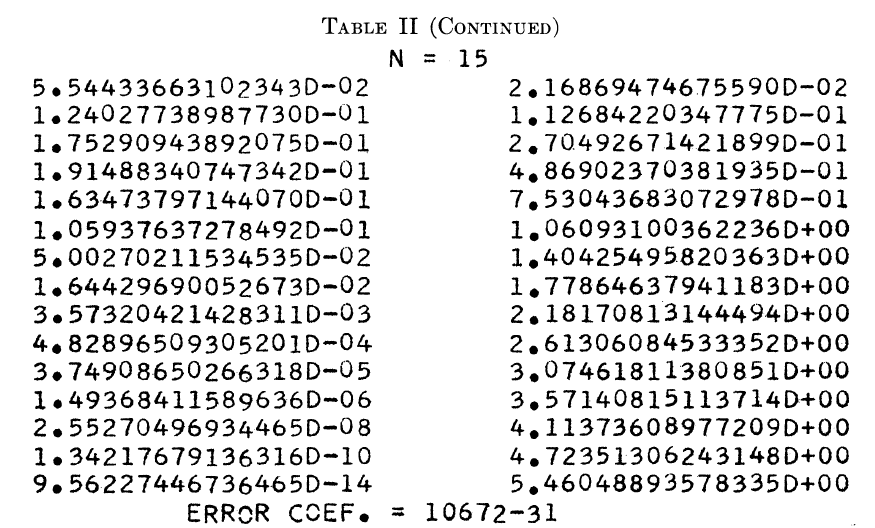
비교해보면 가중치와 특정 지점의 값이 차이가 난다. 처음엔 내 코드가 잘못된 건 줄 알았는데 논문에서 $n=15$인 경우 $\gamma_{15}$의 계산값이 부정확할 수 있다고 한다. 따라서 이러한 부정확성이 가중치와 특정 지점을 계산하는데 영향을 미친 것으로 보인다. 또한 $b=1$로 지정하여 $(0, 1)$ 위에서의 적분값 근사를 위한 가중치와 특정 지점을 계산해보았더니 $n$이 3~8까지는 거의 정확하게 나왔고 9에서 약간의 차이를 보였으며 10에서 특정 지점이 음수값이 나왔다(무조건 양수만 나와야한다).
이 논문은 사실 Dixon's Q Test에서 기각값을 계산할 때 semi-infinite interval에서의 적분을 근사해야 할 필요가 생겨서 읽어보게 된 것이다. 근데 이게 은근 유용하게 쓰일 수 있고 또한 파이썬에서 이러한 적분값을 계산해주는 라이브러리가 없는 것 같아서 내가 나중에 쓰려고 함수를 구현해보았다. 찾아보니까 scipy 라이브러리에서 제공하는 scipy.integrate.quad 함수가 semi-infinite interval에서의 적분값을 계산해주더라.... 그래도 적분을 근사하는 여러 가지 방법에 대해서 알게 된 것 같아 뜻깊은 시간이었다.






댓글