본 포스팅에서는 수식을 포함하고 있습니다.
티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니
웹 브라우저 또는 모바일 웹에서 보시기 바랍니다.
이번 포스팅에서는 William S. Cleveland의 1979 논문인 'Robust Locally Weighted Regression and Smoothing Scatterplots'을 리뷰하고 파이썬을 이용하여 구현해보려고 한다.
이번 포스팅의 구성은 다음과 같다.
6. Estimation and Sampling Distributions for LWR
7. Variance, Bias, and Mean Squared Error for LWR of Degree Zero
Abstract
Robust Locally Weighted Regression(RLWR)은 Smoothing 기법으로 $x$가 주어졌을 때 $x$에서 가까운 점에서는 큰 가중치를, 멀리 떨어진 점은 작은 가중치를 주어 $y$값을 추정한다. 이는 이상치(Outlier)가 모형 적합에 영향을 덜 미치게 함으로써 기존 최소 제곱 회귀 모형이 이상치로 인하여 왜곡될 수 있다는 단점을 보완한 것이다. 이 논문에서는 RLWR의 시각화, 계산문제, 통계적인 이슈를 다룬다.
1. Introduction
이 논문에서는 모의실험을 통하여 Locally Weighted Regression(LWR)의 필요성을 얘기하고 있다.

왼쪽 그림은 $y_i=0.2x_i + \epsilon_i, \; x_i=i, \; \epsilon_i \sim N(0,1)$ 을 이용하여 인위적으로 생성한 데이터의 산포도이다. 그리고 오른쪽 그림은 LWR을 이용하여(정확히 말하면 RLWR) 추정한 곡선을 나타낸다. 이를 통해 단순히 산포도로는 $x$와 $y$의 양의 관계가 잘 보이지 않지만 RLWR을 통하여 양의 관계를 파악할 수 있게 한다. 다시 말하면 LWR은 기존의 산포도가 잡아내지 못하는 데이터의 패턴을 시각적으로 파악할 수 있게 해준다.
RWLR은 기존의 Robust 추정방법인 Iterated Weighted Least Square를 수정한 것이며 Smoothing 기법과 Robust 추정방법의 새로운 아이디어를 접목한 것이다.
2. LWR and RLWR
먼저 이 논문에서 중요한 요소인 가중치 함수 $W$를 살펴보자.
1. $|x|<1$ 에 대하여 $W(x) > 0$
2. $W(-x) = W(x)$
3. $W(x)$는 $x\geq 0$ 에 대하여 증가하지 않는 함수(non-increasing)
4. $|x|\geq 1$에 대하여 $W(x)=0$
여기서 $x$를 두 점 사이의 거리라고 생각하자. 1, 4를 통해 $W$는 음이 아닌 값을 가진다. 따라서 일종의 가중치라고 할 수 있다. 2는 $W$가 대칭이라는 것이다. 이는 특정 위치로부터 왼쪽에 있든 오른쪽에 있든 거리가 같기만 하다면 동일한 가중치를 주겠다는 것이다. 3은 거리가 멀 수록 가중치를 작게 주고 가까울수록 가중치를 크게 준다는 의미이다.
여기서 모형 적합을 위해 2가지 과정을 생각한다.
1) Local Weighted Regression(LWR)
이는 가중치 함수를 이용하여 가중 최소 제곱 회귀 모형을 적합한다는 것을 뜻한다.
2) Robust Locally Weighted Regression(RLWR)
1)에서 구한 모형을 이용하여 잔차를 계산한다. 그리고 새로운 가중치 함수를 도입하여 가중치를 구한다. 이 함수는 잔차 절대값이 클 수록 작고 잔차 절대값이 작을수록 큰 값을 갖는다. 이때 계산된 가중치를 이용하여 다시 가중 최소 제곱 회귀 모형을 적합한다. 이런 식으로 잔차가 큰 데이터가 모형 적합에 영향을 덜 미치도록 한다. 이 과정을 회귀계수가 수렴할 때까지 반복한다. 1) 과정은 LWR이며 1) 과정과 2) 과정을 모두 종합한 것이 RLWR이다.
구체적인 LWR과 RLWR의 알고리즘을 살펴보자.
먼저 $f$는 사전에 정해줘야 할 매개변수이며 $(0, 1]$중에서 택한다. 그리고 $r$을 $fn$과 가장 가까운 정수라고 하자. 다음으로 $h_i$를 $x_i$로부터 $r$번째로 가까운 점과의 거리라고 하자. 즉, 주어진 $x_i$에 대하여 $d_j=|x_j-x_i|$라 하면 $d_j$를 오름차순으로 정렬했을 때 $r$번째 값이 $h_i$가 되는 것이다. 그리고 $w_k(x_i)=W((x_k-x_i)/h_i)$라 하자. 이제 모형 적합 알고리즘을 구체적으로 살펴보자.
Algorithm
1. 주어진 $x_i$에 대하여 $d$차 다항식을 가중 최소 제곱법을 이용하여 적합한다. 즉, 아래의 값을 최소화하는 $\beta_j \;\; j=1,\ldots, d$를 구한다.
$$\sum_{k=1}^nw_k(x_i)(y_k-\beta_0 - \beta_1x_k - \cdots \beta_dx_k^d)^2$$
이때 $\beta_j$의 추정값을 $\hat {beta}_j$이라 하면 $x_i$에서의 적합값 $\hat{y}$는 다음과 같다.
$$\hat{y}_i=\sum_{j=0}^d\hat{\beta}_jx_i^j=\sum_{k=1}^nr_k(x_i)y_k\tag{1}$$
여기까지만 수행했다면 이는 LWR이다.
2. $B$를 다음과 같이 정의하자.
$$\begin{align}B(x) &= (1-x^2)^2, & \text{for} |x|<1 \\ &= 0, & \text{for} |x| \geq 1\end{align}$$
다음으로 $e_i = y_i-\hat{y}_i$라 하자. 즉 $e_i$는 잔차이다. 그리고 $s = \text{median}|e_i|$라 하자. 새로운 가중치 $\delta_k=B(e_k/6s)$를 계산한다.
3. 원 데이터 $(x_k, y_k), \;\;(k=1, \ldots, n)$ 과 r가중치 $\delta_kw_k(x_i)$를 이용하여 가중 최소 제곱 모형을 적합한다.
4. 2~3을 $t$번 반복한다.
1번 과정을 수행하고 2~4 과정을 수행한 경우가 바로 이 논문의 핵심인 RLWR이다.
알고리즘 2단계에서 사용한 함수 $B$를 Bisquare 함수라고 하는데 이 함수를 사용한 이유는 Robust 추정법에서 좋은 성능을 보였다고 알려졌기 때문에 사용했다고 한다. RLWR을 이용하여 계산한 적합값을 이용하여 곡선을 그릴 수 있는데 이를 원 데이터의 산포와 같이 그려놓는다면 데이터의 패턴을 시각적으로 표현할 수 있어서 좋다.
3. Example
3.1 Abrasion Loss Data
이 논문에서는 Abrasion Loss Data를 이용하여 Abrasion Loss와 Tensile Strenth의 Partial Regression Plot을 그려보고 여기에 LWR과 RLWR 모형을 적용시키고자 한다. 이때 RWLR에서 알고리즘 2~3단계 반복 횟수 $t=2$로 설정하였으며 LWR, RLWR 양쪽 모두 $f=0.5, d=1$을 선택하였다. 그리고 $W$는 tricube 함수로 설정하였다.
$$\begin{align}W(x) &= (1-|x|^3)^3, & \text{for} |x|<1 \\ &= 0, & \text{for} |x| \geq 1\end{align}$$
아래 그림은 LWR(점선), RLWR(실선)을 적합한 것이다.

Robust 과정(알고리즘 2~3단계)을 거치지 않은 LWR의 경우 좌측 하단의 이상치에 영향을 받고 있는 것을 알 수 있으며 RLWR의 경우 이상치의 덜 영향을 받고 있다.
구현해보기!!
나는 이 부분을 파이썬으로 구현해보았다. 먼저 데이터를 다운받아준다.
그리고 필요한 모듈을 임포트하고 데이터를 불러온다. Abrasion Loss Data은 DAT 파일이며 탭으로 구분되어있다. 이는 Pandas에서 제공하는 read_csv를 이용하여 읽을 수 있다.
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.formula.api import ols
import statsmodels.api as sm
names = ['abrasion_loss','hardness','tensile_strength']
df = pd.read_csv('ABRASION.DAT',sep='\t',names=names)
Partial Regression Plot을 그리기 위하여 abrasion_loss를 반응 변수, hardness를 설명변수로 하는 선형 회귀 모형과 tensile_strength를 반응변수, hardness를 설명변수로하는 선형 회귀 모형을 적합한다.
fit1 = ols('abrasion_loss~hardness',data=df).fit()
fit2 = ols('tensile_strength~hardness',data=df).fit()
각 모형에서 잔차를 구하고 이를 데이터프레임으로 만들어준다.
resid_df = pd.DataFrame()
resid_df['x'] = fit2.resid
resid_df['y'] = fit1.resid
resid_df = resid_df.sort_values('x')
그리고 bicube, tricube 함수와 주어진 점으로부터 가까운 점들을 구하는 함수를 만들었다.
def bisquare(x):
x = abs(x)
res = []
for v in x:
if v < 1:
res.append((1-v**2)**2)
else:
res.append(0)
return np.array(res)
def tricube(x):
x = abs(x)
res = []
for v in x:
if v < 1:
res.append((1-v**3)**3)
else:
res.append(0)
return np.array(res)
def get_n_th_distance(x, y, n):
y = np.array(y)
distances = abs(y-x)
return np.partition(distances, n-1)[n-1]
이제 LWR 모형을 적합한다.
## LWR
f = 0.5
n = len(resid_df)
r = int(round(f*n))
x_s = resid_df['x']
nr_fitted_value = []
for x in x_s:
h = get_n_th_distance(x,resid_df['x'],r)
weights = tricube((x-resid_df['x'])/h)
idx = np.where(weights>0)[0]
X = resid_df['x']
X = sm.add_constant(X)
y = resid_df['y']
fit = sm.WLS(y, X, weights).fit()
fitted_val = fit.params['const'] + fit.params['x']*x
nr_fitted_value.append(fitted_val)
다음으로 RLWR 모형을 적합한다.
## RLWR
f = 0.5
t = 2
n = len(resid_df)
r = int(round(f*n))
count = 1
x_s = sorted(resid_df['x'])
fitted_value = []
## 알고리즘 1단계
for x in x_s:
h = get_n_th_distance(x,resid_df['x'],r)
weights = tricube((x-resid_df['x'])/h)
idx = np.where(weights>0)[0]
X = resid_df['x']
X = sm.add_constant(X)
y = resid_df['y']
fit = sm.WLS(y, X, weights).fit()
fitted_val = fit.params['const'] + fit.params['x']*x
fitted_value.append(fitted_val)
fitted_value = np.array(fitted_value)
## 알고리즘 2~3단계 t번 반복
while count <= t:
count += 1
abs_residual = abs(resid_df['y'] - fitted_value)
s = np.median(abs_residual)
delta = bisquare((resid_df['y']-fitted_value)/(6*s))
new_fitted_value = []
for x in x_s:
h = get_n_th_distance(x,resid_df['x'],r)
weights = delta*tricube((x-resid_df['x'])/h)
idx = np.where(weights>0)[0]
X = resid_df['x']
X = sm.add_constant(X)
y = resid_df['y']
fit = sm.WLS(y, X, weights).fit()
fitted_val = fit.params['const'] + fit.params['x']*x
new_fitted_value.append(fitted_val)
new_fitted_value = np.array(new_fitted_value)
fitted_value = new_fitted_value
다음으로 LWR, RLWR의 적합 결과를 그래프로 나타내었다.
앞의 그림과 정확히 일치한다.
바로 위의 그림에서 알 수 있듯이 데이터 간에 비선형인 패턴이 보이므로 선형 회귀 모형을 적합하지 않다는 것을 알 수 있다.
3.2 Residuals vs Fitted Values
보통 오차의 등분산성을 확인하기 위하여 잔차도를 많이 이용한다. 이 때 x축에는 적합값 $\hat{y}$, y축에는 잔차 $e_i$를 그리는데 이러한 잔차도는 오차의 등분산성 가정을 제대로 파악할 수 없다고 한다. 아래의 그림을 살펴보자.

얼핏 보기에는 적합값이 증가함에 따라 잔차도의 범위가 증가하는 것처럼 보인다. 따라서 오차의 등분산성이 만족되지 않는다고 판단할 수있다. 하지만 이는 잘못된 판단일 수도 있다. 왜냐하면 적합값이 증가할수록 데이터의 밀도가 증가하는데(다시 말해 데이터 수가 많아지는데) 이에 따라 잔차도의 범위가 증가했을 수도 있기 때문이다. 이러한 문제점으로 인하여 y축에 잔차 대신 잔차의 절대값을 이용하는 것이 좋다고 한다.
위의 데이터를 잔차의 절대값으로 바꾼 산포도와 RLWR 모형을 적합(실선)한 그림이 아래와 같다.

실선을 보면 잔차의 범위가 증가하는 패턴이 뚜렷하게 보이지 않는다. 따라서 오차의 등분산성을 만족한다고 볼 수 있다. 다시 한번 RLWR이 데이터 패턴을 시각화하여 확인하는데 아주 강력한 도구가 될 수 있다는 것을 보여준다.
3.3 Lead Intoxication
연프로토포르피린(ZPP)과 혈액 속 납 함량의 관계를 시각적으로 보고자 했다. 이 부분도 구현하려고 했으나 데이터를 찾지 못해서 패스한다.
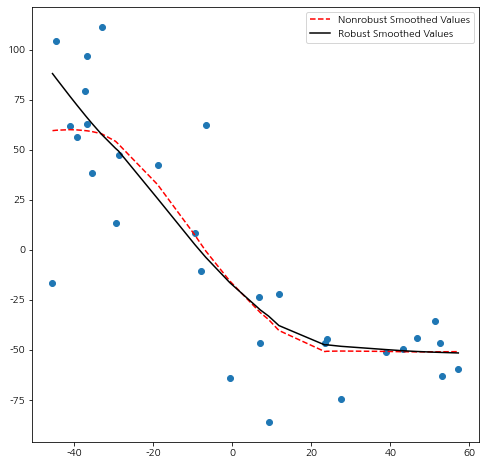
아래 그림은 혈중 납 함량과 ZPP의 데이터 산포도와 RLWR 모형(실선)을 나타낸 것이다.

데이터 패턴을 보면 ZPP가 0~400인 구간에서 2차 함수(오목 함수) 같은 형태를 띠고 400을 넘어가는 구간부터 혈중 납 함량이 일정하게 유지된다. 논문의 저자는 이러한 데이터 패턴을 찾기 위하여 모수를 이용한 모형을 사용할 수 있겠으나 논문에서 제시한 RLWR 보다는 모형을 적합하는데 더 노력이 든다고 한다. 즉, RLWR이 데이터 패턴을 파악해줄 뿐만 아니라 다른 모형에 비해서 쉽게 구현이 가능하다고 주장하는 것이다.
4. Choosing Parameter
4.1 Choosing $d$
저자는 $d$의 값을 1로 설정하는 것을 추천하고 있다. 왜냐하면 $d=1$인 경우 계산의 간편함과 데이터 패턴을 있는 그대로 잡아내는데 적합한 값이기 때문이라고 한다. $d=0$은 $d=1$인 경우보다 계산이 간편하지만 실제 데이터 분석 시에는 $d=1$이 훨씬 더 좋다고 한다. $d=2$인 경우는 데이터의 패턴을 좀 더 정교하게 잡아낼 수 있다는 이득이 있지만 그러한 이득보다 계산의 복잡으로 인한 손해가 더 커서 $d=1$을 쓰는 것을 추천하고 있다. 하지만 컴퓨터가 옛날보다 더 좋아졌으니 $d$를 2 이상의 값으로 설정하는 것도 고려해보자.
4.2 Choosing $W$
$W$의 경우 $x$가 0에서 1로 증가할 때 스무스하게 줄어드는 함수가 좋다고 한다. 왜냐하면 이런 성질을 만족하는 가중치 함수 $W$가 데이터의 패턴을 매끄럽게 표시해주기 때문이다. 여기서는 $W$를 Tricube 함수를 사용했는데 그 이유는 오차항의 분산 추정량을 근사적으로 카이제곱 분포를 따르게 할 수 있다고 한다.
4.3 Choosing $t$
Robust 단계(알고리즘 2~3단계) 반복 횟수 $t$ 는 2번 정도면 적당하다고 한다. 이는 수많은 실제 데이터와 모의실험을 통해 알아낸 것이라 한다.
4.4 Choosing $f$
$f$ 는 주어진 점으로부터 데이터를 몇 개를 쓸 것인지를 결정하는 매개변수이다. 따라서 이 값이 증가할수록 모형의 그래프는 매끄러워진다. 여기서 데이터의 패턴을 왜곡시키지 않으면서 최대한 매끄럽게 패턴을 시각화할 수 있는 $f$를 선정해야 한다. 저자는 필요한 정보가 없다면 $f=0.5$로 시작하는 것이 합리적이라고 주장한다. 회귀 모형을 선택하는 기준으로 PRESS 통계량이 있는데 이를 최적의 $f$를 찾는 문제에 사용될 수 있다고 한다. PRESS에 대한 설명은 여기를 참고하기 바란다.
먼저 아래의 함수를 최소화하는 $f_0$를 찾는다.
$$\sum_{k=1}(y_k-\hat{y}_k(f))^2$$
여기서 $$\hat{y}_i(f)$$는 $i$ 번째 데이터를 뺀 모형에서 $x_i$에 대한 적합값이다. 최소화하는 과정에선 $f$를 0부터 1 사이의 값을 후보로 정하고 greedy 알고리즘 방식으로 최소화하는 $f_0$를 찾는다.
다음 단계에서는 위에서 구한 $\hat{y}_k(f)$를 이용하여 아래의 값을 최소화하는 $f$를 찾는다.
$$\sum_{k=1}\delta_k(y_k-\hat{y}_k(f))^2$$
이 단계를 $f$가 수렴할 때까지 반복한다.
5. Computation
5.1 Reducing the Computation
Tricube 함수와 같은 가중치 함수는 특정 거리보다 멀어진 데이터에 대해서는 0이기 때문에 모형 적합값 $\hat{y}_i$을 구하는 데 있어서 오직 $r$의 데이터만 필요하다. 여기서는 $x_i$의 근접 이웃(Nearest Neighbor)를 이용하여 $x_{i+1}$의 근접 이웃을 구하는 효율적인 방법을 제공하고 있다. 따라서 매번 새롭게 $r$개의 근접 이웃을 구할 필요가 없으므로 계산량이 줄어든다는 이점이 있다. 오늘날에는 이것이 그렇게 중요하지 않을 수 있는데 컴퓨터가 좋지 않았던 옛날에는 계산을 좀만 줄여줘도 효과가 컸나 보다.
5.2 Grouping
모형은 같은 $x$값에 대하여 같은 $\hat{y}$을 출력한다. 따라서 $x$값과 그에 대한 적합값 $\hat{y}$를 일종의 참조테이블 형식으로 저장해두고 주어진 $x$가 저장한 데이터 중에 하나라면 적합값을 참조테이블에서 바로가져오고 새로운 값이라면 그제서야 적합값을 계산하도록 추천하고 있다. 이런식으로 계산량을 줄인다.
6. Estimation and Sampling Distributions for LWR
6.1 Estimation of the Error Variance and the Standard Errors of Fitted Values for Normal $\epsilon_i$
오차의 분산 추정량과 LWR 모형 적합값 $\hat{y}$의 표준 오차를 계산하기 위해 오차 $\epsilon_i$가 서로 독립이고 $N(0,\sigma^2)$을 따른다고 가정했고 추가적으로 $\hat{y}$의 편의를 무시할 정도로 작다고 가정했다(이 가정의 정당성에 대해서는 심히 의심스럽다).
먼저 $e_i=y_i-\hat{y}_i$, $R=(r_{ik}), r_{ik}=r_k(x_i)$(식 (1) 참고), $C=(I-R)(I-R)^t$, $t_s=\text{tr}(C^s)$라고 하자. 논문에서는 오차의 분산을 다음과 같이 추정한다.
$$\hat{\sigma}^2=t_1^{-1}\sum_{i=1}^ne_i^2$$
이때 $\hat{\sigma}^2$은 $\sigma^2$의 불편추정량이다.
그리고 적합값 $\hat{y}_i$의 표준오차는 아래와 같이 추정한다.
$$\hat{\sigma}(\sum_{k=1}^nr_k^2(x_i))^{\frac{1}{2}}$$
다음으로 $\hat{\sigma}^2$의 근사분포는 $W$가 Tricube일 경우 $t_1^2t_2^{-1}$에서 가장가까운 정수를 자유도로하는 카이제곱분포라고 한다. 따라서 이를 이용하여 $\hat{\sigma}^2$의 신뢰구간을 근사적으로나마 구할 수 있다.
그리고 논문에서는 $f$의 값을 선택하는 기준으로 활용할 수 있는 $\lambda$를 제시하고 있다. 여기서 $\lambda$는 다음과 같다.
$$\lambda = 2\sum_{i=1}^nr_i(x_i)-\sum_{k=1}^n\sum_{i=1}^nr_k^2(x_i)\tag{2}$$
논문에서는 $d=1$이고 가중치 함수 $W$가 Tricube 함수이니 경우 $2(1+1/f)\approx \lambda$라고 한다. 따라서 이 결과와 식 (2)를 이용하여 $f$의 최적값을 유추해볼 수 있다.
6.2 Estimating the Standard Error of the Fitted Values for More Generally Distributed $\epsilon_i$
6.1에서 오차의 정규분포 가정을 제외할 경우 저자는 RLWR 모형을 적합하는 것이 좋다고 한다. 논문에서는 RLWR 모형 적합값 $\hat{y}_i$의 표준오차를 제시하고 있다. 논문의 저자는 제시한 추정량의 성질을 이해하기 위해서는 더 많은 실험이 필요하다고 한다(실험을 하고 논문을 써야하는거 아닌가? ㄷㄷ;;).
7. Variance, Bias, and Mean Squared Error for LWR of Degree Zero
이 논문에서는 LWR 적합값 $\hat{y}_i$의 분산과 주어진 점 $x$와 $r$ 번째 이웃과의 거리 $h$간의 관계를 밝히고 있다. 일반적으로 $h$가 작아지면 $\hat{y}_i$의 편의(Bias)는 줄어들지만 과적합으로 인하여 분산은 늘어난다. 또한 $h$가 커지면 일반적으로 분산은 줄어들지만 편의는 증가한다. 여기서는 $d=0$인 상황에서 $h$가 증가할수록 $\hat{y}_i$의 분산이 증가하는(정확하게 말하면 감소하지 않는) 필요충분조건이 무엇인지 이론적으로 증명하고 있다.





댓글