이번 포스팅에서는 파이썬(Python) shap 패키지를 이용하여 SHAP Value 계산 방법과 시각화 결과를 어떻게 해석하는지 알아보려고 한다.
SHAP Value에 대한 개념은 아래 포스팅을 참고하기 바란다.
25. Shapley Value와 SHAP에 대해서 알아보자 with Python
25. Shapley Value와 SHAP에 대해서 알아보자 with Python
이번 포스팅에서는 게임 이론에서 상금 분배 방법의 하나인 Shapley Value와 이를 머신러닝 예측 모형을 해석하는 데 활용한 SHAP에 대해서 알아보고자 한다. 그리고 SHAP Value를 계산하는 과정을 파이
zephyrus1111.tistory.com
SHAP Value 계산 및 시각화 결과 해석하기
- 목차 -
1) shap 패키지 설치
shap 패키지가 없다면 아래 코드를 복사해서 설치를 해줘야 한다.
pip install shap2) SHAP Value 계산
여기에서는 보스턴 집값 데이터를 이용하여 랜덤포레스트 회귀 모형을 학습해 주었다.
from sklearn.datasets import load_boston
from sklearn.ensemble import RandomForestRegressor
## 보스턴 집값 데이터
boston = load_boston()
X = boston.data
y = boston.target
## 모형 학습
reg = RandomForestRegressor(n_estimators=50, max_depth=5, random_state=0).fit(X, y)a. SHAP Value 계산
Exact SHAP Value
정확한 SHAP Value를 계산하는 방법을 살펴보자.
먼저 예측하고자 하는 데이터를 만들고 해당 데이터에 대한 랜덤 포레스트 회귀모형의 예측값을 계산했다.
Exact SHAP Value는 Explainer를 이용하면 된다. 여기에 학습이 완료된 모형과 학습에 사용된 X 데이터를 넣어준다. 그런 다음 expected_value 속성을 통해서 Base Value를 shap_values 속성을 통해서 SHAP Value를 계산할 수 있다. 이때 예측값이 Base Value와 SHAP Value의 합과 같은지 살펴보았다.
idx = 1
X_data = X[idx, :].reshape(1, X.shape[1]) ## 예측하고자할 데이터
predicted_value = reg.predict(X_data)[0] ## 예측값
explainer = shap.Explainer(reg, X) ## Explainer 객체 생성
expected_value = explainer.expected_value ## Base SHAP Value
shap_values = explainer.shap_values(X_data) ## SHAP Value
print('SHAP Value :', shap_values)
print('예측값 :', predicted_value)
print('SHAP Value 합 :', np.sum(shap_values)+expected_value)

코드를 실행해 보았더니 예측값과 Base Value와 SHAP Value의 합이 약간의 차이를 보였다.
Kernel SHAP Value
Kernel SHAP Value는 KernelExplainer를 이용하여 계산할 수 있다. 이때 주의할 점은 학습된 모형을 넣는 것이 아닌 predict 메서드를 넣어줘야 한다는 것이다.
idx = 1
X_data = X[idx, :].reshape(1, X.shape[1]) ## 예측하고자할 데이터
predicted_value = reg.predict(X_data)[0] ## 예측값
kernel_explainer = shap.KernelExplainer(reg.predict, X) ## KernelExplainer 객체 생성
expected_value = kernel_explainer.expected_value ## Base SHAP Value
shap_values = kernel_explainer.shap_values(X_data) ## SHAP Value
print('SHAP Value :', shap_values)
print('예측값 :', predicted_value)
print('SHAP Value 합 :', np.sum(shap_values)+expected_value)

Kernel SHAP Value는 시간이 좀 걸린다. Exact SHAP Value와는 다르게 예측값과 Base Value, SHAP Value의 합이 정확히 일치했다.
Tree SHAP Value
만약 학습 모형이 나무 기반(예: 랜덤 포레스트)으로 되어 있다면 Tree SHAP Value를 생각해 볼 수 있는데 TreeExplainer를 사용하면 쉽게 계산할 수 있다. 사용 방법은 TreeExplainer에 학습된 모형과 학습 데이터를 넣어주면 된다.
idx = 1
X_data = X[idx, :].reshape(1, X.shape[1]) ## 예측하고자할 데이터
predicted_value = reg.predict(X_data)[0] ## 예측값
tree_explainer = shap.TreeExplainer(reg, X) ## TreeExplainer 객체 생성
expected_value = tree_explainer.expected_value ## Base SHAP Value
shap_values = tree_explainer.shap_values(X_data) ## SHAP Value
print('SHAP Value :', shap_values)
print('예측값 :', predicted_value)
print('SHAP Value 합 :', np.sum(shap_values)+expected_value)

Exact SHAP Value와 마찬가지로 예측값과 Base Value와 SHAP Value의 합이 약간의 차이를 보였다.
b. 변수 중요도(Feature Importance)
SHAP Value를 이용하면 각 변수의 (Global) 변수 중요도를 계산할 수 있다.
tree_explainer = shap.TreeExplainer(reg) ## TreeExplainer 객체 생성
shap_values = tree_explainer.shap_values(X) ## SHAP Value
feature_names = boston.feature_names ## 변수명
## 변수 중요도
for i in range(X.shape[1]):
feature_imp = np.mean(np.abs(shap_values[:, i]))
print(f'{feature_names[i]}의 중요도 :', feature_imp)

3) 시각화 결과 해석
shap에서는 summary_plot을 사용하여 SHAP Value를 시각적으로 확인할 수 있다. summary_plot은 점 그림(Dot Plot)과 막대 그림(Bar Plot)을 많이 쓰는데 이 2개의 그림을 그려보는 방법과 어떻게 해석하는지 알아보자.
a. 점 그림(Dot Plot)
summary_plot에서 plot_type을 지정하지 않으면 기본적으로 점 그림(Dot Plot)을 그려준다. summary_plot에 SHAP Value로 구성된 매트릭스와 X 매트릭스를 넣어주면 된다. 나머지 인자는 주석을 참고하자.
## Dot Plot
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False
tree_explainer = shap.TreeExplainer(reg) ## TreeExplainer 객체 생성
shap_values = tree_explainer.shap_values(X) ## SHAP Value
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
shap.summary_plot(shap_values, X,
feature_names=boston.feature_names, ## 변수명 표시
cmap='bwr', ## 컬러맵
show=False, ## 기존 X축 라벨 표시 안함
)
ax.set_xlabel('SHAP Value')
ax.set_title('SHAP Dot Plot', fontsize=20)
plt.show()

※ 그림 해석 ※
SHAP Dot Plot은 SHAP Value와 X 인자 간의 상관관계를 알 수 있고 이를 통해 X 인자가 예측에 어떤 방향으로 영향을 미쳤는지 알 수 있다.
예를 들어 위 그림에서 LSTAT 변수는 SHAP Value가 음수인 곳에서 빨간색 점들이 압도적으로 많고 SHAP Value가 양수인 곳에서 파란색 점들이 많다.
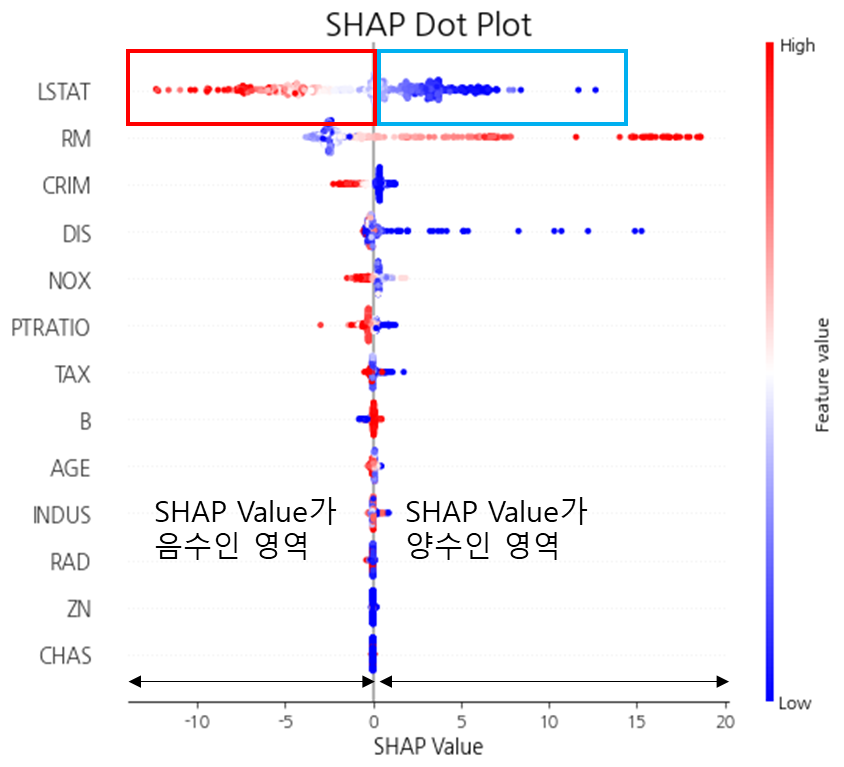
이때 SHAP Value가 음수라는 것은 예측값을 감소시켰다는 것을 의미하며 양수는 예측값을 증가시켰다는 것을 의미한다. 그리고 SHAP Value가 음수인 곳에서 빨간 점들이 많이 분포한다는 것은 LSTAT 값이 높을 때 예측값을 감소시켰다는 것이며 반대로 SHAP Value 양수인 곳에서 파란점들이 많다는 것은 LSTAT 값이 낮을 때 예측값을 증가시켰다는 것이 된다. 따라서 전체적으로 보았을 때 LSTAT는 예측값에 음의 상관성으로 영향을 미쳤다는 것을 알 수 있다.
마찬가지로 RM은 SHAP Value가 음수인 곳에서 파란점들이 많고 SHAP Value 양수인 곳에서빨간 점이 많은 것을 알 수 있다. 따라서 RM은 LSTAT와는 다르게 예측값에 양의 상관성으로 영향을 미쳤다는 것을 알 수 있다.
점 그림(Dot Plot)을 이용할 때 어떤 인자가 SHAP Value가 0이 되는 지점을 좌우로 하여 색깔 또한 나뉘게 된다면 해당 변수는 특정 방향으로 예측값에 영향을 미쳤다는 것이 되므로 그 인자는 우선적으로 살펴볼 필요가 있다.
b. Bar Plot
summary_plot에서 plot_type='bar'로 지정하면 않으면 기본적으로 막대 그림(Bar Plot)을 그려준다. 그리는 방법은 점 그림을 그리는 법과 동일하다.
## Bar Plot
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False
tree_explainer = shap.TreeExplainer(reg) ## TreeExplainer 객체 생성
shap_values = tree_explainer.shap_values(X) ## SHAP Value
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
shap.summary_plot(shap_values, X,
feature_names=boston.feature_names, ## 변수명 표시
plot_type='bar', ## 막대 그래프
color='k', ## 막대 컬러
show=False ## 기존 X축 라벨 표시 안함
)
ax.set_xlabel('SHAP Value')
ax.set_title('SHAP Bar Plot', fontsize=20)
plt.show()

※ 그림 해석 ※
막대 그림(Bar Plot)에서 막대의 (가로) 길이는 개별 변수의 SHAP Value의 절대값 평균을 취한 것으로 글로벌한 예측 영향 정도이라고 생각할 수 있다. 따라서 어떤 변수에 대응하는 막대 길이가 길수록 글로벌한 예측 영향력이 크고 이는 예측에 있어서 중요한 변수라고 생각할 수 있다. 다만 점 그림(Dot Plot)과 같은 영향의 방향성 정보는 제공하지 못한다는 단점이 있다.
c. Depedence Plot
Dependence Plot을 이용하면 예측에 영향을 주는 인자들의 교호작용(Interaction)을 확인할 수 있다.
Dependence Plot은 shap에서 dependence_plot 함수를 이용하면 된다. 이 함수는 변수 인덱스, SHAP Value로 이루어진 2차원 매트릭스, X 매트릭스를 기본적으로 받게 된다. 아래 코드는 변수 인덱스가 6(7번째 변수)인 Age 변수의 Dependence Plot을 그린 것이며 Age 변수와 가장 교호작용 효과가 큰 LSTAT와의 교호 작용을 확인할 수 있다.
## Bar Plot
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False
tree_explainer = shap.TreeExplainer(reg) ## TreeExplainer 객체 생성
shap_values = tree_explainer.shap_values(X) ## SHAP Value
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
ax = fig.add_subplot()
shap.dependence_plot(6, shap_values, X,
feature_names=boston.feature_names, ## 변수명 표시
ax = ax, ## 현재 좌표축
cmap = 'bwr' ## 컬러맵
)
ax.set_title('SHAP Dependence Plot', fontsize=20)
plt.show()

※ 그림 해석 ※
먼저 AGE 변수는 전반적으로 80세 이상에서는 예측값을 감소시키는 쪽으로 영향을 미치고 있고 80세 미만에서는 예측값을 증가시키는 쪽으로 영향을 미치고 있다.

이때 80세 이상에서 LSTAT 값이 대체로 큰 것(빨간 점)을 알 수 있고 80세 미만에서 LSTAT값이 대체로 작은 것을 알 수 있다. 따라서 AGE 변수가 예측에 영향을 미치는 방향이 LSTAT 수준에 따라서 바뀌고 있다는 것을 알 수 있으며 이는 정확히 AGE 변수와 LSTAT 간의 교호작용(Interaction)이 있음을 뜻한다.
shap에서 그려주는 Dependence Plot을 확인할 때 가장 이상적인 경우는 아래와 같이 x축에 대응하는 변수가 SHAP Value에 대하여 대각선 분포(양의 상관관계 또는 음의 상관관계) 형태이고 이 대각선과 SHAP Value 값이 0이 되는 선이 만나는 대략적인 x좌표를 기준으로 교호작용을 확인할 변수의 분포가 나뉘는 것이다.

'프로그래밍 > 기타 Python 모듈' 카테고리의 다른 글
| Pyinstaller 기본 - 이용하여 파이썬(.py) 파일을 실행 파일(.exe)로 만들기 (1) | 2023.03.17 |
|---|---|
| [오류 해결] Pyinstaller : ValueError: not enough values to unpack (expected 2, got 1) (1) | 2023.03.17 |
| [imageio] 파이썬(Python)으로 이미지 파일을 모아서 gif 파일 만들기 (0) | 2023.01.23 |
| [XGBoost] XGBoost 모형 학습하기 (feat. XGBClassifier, XGBRegressor) (0) | 2022.11.05 |
| [Jupyter Notebook] 주피터 노트북 크롬(Chrome)으로 바로 실행하기 (2) | 2022.10.21 |





댓글