이번 포스팅에서는 Change Point Detection 알고리즘의 하나인 CUSUM(CUmulative SUM) 알고리즘에 대한 개념을 알아보고자 한다. 또한 파이썬(Python)으로 구현하는 과정과 예제를 통하여 알고리즘의 작동 원리를 살펴보고자 한다.
- 목차 -
1. CUSUM 알고리즘
1) 문제 정의
CUSUM 알고리즘이 풀고자 하는 문제는 시계열 내에 급격한 변경점이 없다는 가설 $H_0$와 하나의 변경점이 있다는 가설 $H_a$을 세우고 $H_0$과 $H_a$ 중에 어떤 것을 선택해야 하는 문제가 있다. 이 문제만 해결되면 변경점은 자연스럽게 추정할 수 있다. 이를 구체적으로 살펴보자.
먼저 시계열 데이터 $X_t, t=1, 2, \ldots, k$가 있다고 하자. 이때 $X_t$는 독립이고 확률 밀도 함수 $p_{\theta}(x)$를 갖는 확률 분포로부터 나왔다고 가정해보자.
Change Point Detection 알고리즘은 시계열 데이터에서 갑작스러운 변화가 생겼을 경우에 해당하는 시점 $t_c$을 찾게 된다. 이러한 변화를 모델링하기 위해 $\theta$를 변화 시점 전과 후로 다르게 세팅한다. 예를 들어 $t_c$ 이전엔 $\theta = \theta_0$, $t_c$ 이후엔 $\theta = \theta_1$으로 설정하는 것처럼 말이다.
이 경우 시계열 내에 급격한 변화가 없다는 귀무가설 $H_0$을 세운다면 $H_0$ 하에서 다음을 알 수 있다.
$$ p_{H_0}(\tilde{x}) = p_{H_0}(x_1, \ldots, x_k) = \prod_{t=1}^kp_{\theta_0}(x_t) \tag{1}$$
여기서 $\tilde{x} = (x_1, \ldots, x_k)$이다.
그리고 하나의 급격한 변화 시점이 있다는 대립 가설 $H_a$ 하에서 다음을 알 수 있다.
$$p_{H_a}(\tilde{x}) =p_{H_a}(x_1, \ldots, x_k) = \prod_{t=1}^{t_c}p_{\theta_0}(x_t)\prod_{t=t_c+1}^kp_{\theta_1}(x_t) \tag{2}$$
이제 $H_0$과 $H_a$ 중에 어떤 가설을 선택해야 하는지에 관한 문제가 발생하게 된다. $H_0$, $H_a$ 결정 문제는 다음 섹션에서 알아보자.
2) CUSUM 알고리즘
CUSUM 알고리즘은 개별 로그 우도비의 누적합을 이용하여 이 누적합이 사용자가 지정한 상한선을 넘어갔을 경우 시계열의 변경점 존재한다고 알려주는 알고리즘이다.
위에서 정의한 내용을 하나씩 파헤쳐 보자.
(1) $H_0$ vs $H_a$
이제 $H_0$와 $H_a$ 중에 어떤 가설을 선택해야 할 것이다. 우리는 $H_0$, $H_a$ 하에서 확률 밀도 함수를 알고 있으므로 우도 함수(Likelihood Function)를 알 수 있고 그에 따라 로그 우도 함수(Log Likelihood Function)를 알 수 있다. 이는 곧 로그 우도비를 생각할 수 있다는 것과 같다. (1)과 (2)를 이용하여 로그 우도비(Log Likelihood Ratio)를 써보면 다음과 같다.
$$LLR = \log\frac{p_{H_0}(\tilde{x})}{p_{H_a}(\tilde{x})} \tag{3}$$
$LLR$이 클수록 대립 가설 $H_a$을 지지하게 되므로 변경점이 있다는 뜻이 된다. 이때 사용자가 지정한 양수 $h$에 대하여 $LLR > h$이면 $H_a$를 채택하게 되는 것이다. (3)을 (1)과 (2)를 이용하여 다시 계산하면 다음과 같다.
$$LLR(k, t_c) = \sum_{t=t_c+1}^k\log\left ( \frac{p_{\theta_1}(x_t)}{p_{\theta_0}(x_t)} \right ) \tag{4}$$
이때 로그 우도비 $LLR$이 $k, t_c$에 의존한다는 것을 부각했다.
먼저 $\theta_0, \theta_1$을 알고 있다고 가정해 보자(모르는 경우는 뒤에 가서 다룰 것이다). 그럼에도 불구하고 $LLR$은 아직 계산할 수 없다. 왜냐하면 $t_c$를 모르기 때문이다. 이때 Kay라는 사람이 기가 막힌 방법(이 방법을 Generalized Likelihood Ratio Test라 한다)을 제안했다. 바로 모든 $t_c=1, \ldots, k$에 대하여 $LLR$을 계산한 뒤 이 중에서 최대값(이건 계산할 수 있다)을 검정 통계량으로 하는 것이다. 이를 수식으로 나타내면 다음과 같다.
$$\begin{align} G(k) &= \max_{1\leq t_c \leq k} LLR(k, t_c) \\ &= \max_{1\leq t_c \leq k} \sum_{t=t_c+1}^k\log\left ( \frac{p_{\theta_1}(x_t)}{p_{\theta_0}(x_t)} \right ) \end{align}\tag{5}$$
그러면 $G(k) > h$인 경우 $H_a$를 선택하고 아니면 $H_0$를 선택한다. 이때 $G(k)$를 의사결정 함수라 한다(또는 일반화 우도비라고도 한다).
(2) 변경 시점 $t_c$ 추정
만약 $G(k)>h$이고 그에 따라 $H_a$를 선택했을 때 $G(k)>h$을 만족하는 최초 $k$를 $k'$라 하자. 변경 시점이 있다는 것이므로 변경 시점을 추정해야 한다. 이때 $LLR(k, t_c)$를 크게 하는 시점을 변경 시점으로 추정하게 된다.
$$\DeclareMathOperator*{\argmaxA}{arg\,max} \hat{t}_c = \argmaxA_{1\leq t_c \leq k'}LLR(k, t_c)\tag{6}$$
(3) 의사결정 함수의 다른 표현식
a. 일반형
이번엔 다른 방식으로 의사결정 함수를 살펴보고자 한다.
먼저 $s(n)$을 다음과 같이 정의한다.
$$s(n) = LLR(n, n) = \log \left( \frac{p_{\theta_1}(x_n)}{p_{\theta_0}(x_n)} \right) \tag{7}$$
이를 개별 로그 우도비(Instantaneous Log Likelihood Ratio)라 한다.
그러면 $s$의 1부터 $k$ 까지의 누적합(Cumulative Sum) $S(k)$는 다음과 같다.
$$S(k) = \sum_{n=1}^ks(n) \tag{8}$$
누적합을 이용하여 (4)를 다시 표현하면 다음과 같다.
$$LLR(k, t_c) = S(k) - S(t_c) \tag{9}$$
(9)를 (5), (6)에 적용하면 다음을 알 수 있다.
$$\begin{align}G(k) &= S(k) - \min_{1\leq t_c \leq k}S(t_c) \\ &= S(k)-m(k) \end{align} \tag{10}$$
$$\DeclareMathOperator*{\argminA}{arg\,min} \hat{t}_c = \argminA_{1\leq t_c \leq k'}S(t_c) \tag{11}$$
여기서 $m(k) = \min_{1\leq t_c \leq k}S(t_c)$ 이고 $k' = \inf \{ k: G(k) > h\}$이다 .
여기서 알 수 있는 것은 앞에서 살펴본 변경점 존재 여부를 나타내는 알고리즘은 개별 로그 우도비의 누적합으로 표현될 수 있다는 것이며 알고리즘 명칭인 CUSUM은 이러한 누적합으로부터 알고리즘이 도출되었다는 것을 의미한다.
이때 일반화 우도비 $G(k) = S(k)-m(k)$를 일반형이라고 하겠다.
개별 로그 우도비 누적합과 변경점 존재 여부와의 관련성을 살펴보자. 여기서는 설명의 편의를 위하여 $\theta_0, \theta_1$을 알고 있다고 가정하겠다. 만약 변경점이 없는 상태가 유지되는 경우 다시 말해 $X_t$의 확률 밀도 함수가 $p_{\theta_0}(x_t)$를 유지하는 경우 개별 로그 우도비 $s(t)$은 음수를 유지하므로 $t$시점까지의 누적합 $S(t)$는 계속해서 작아질 것이다(아래 그림 참고).
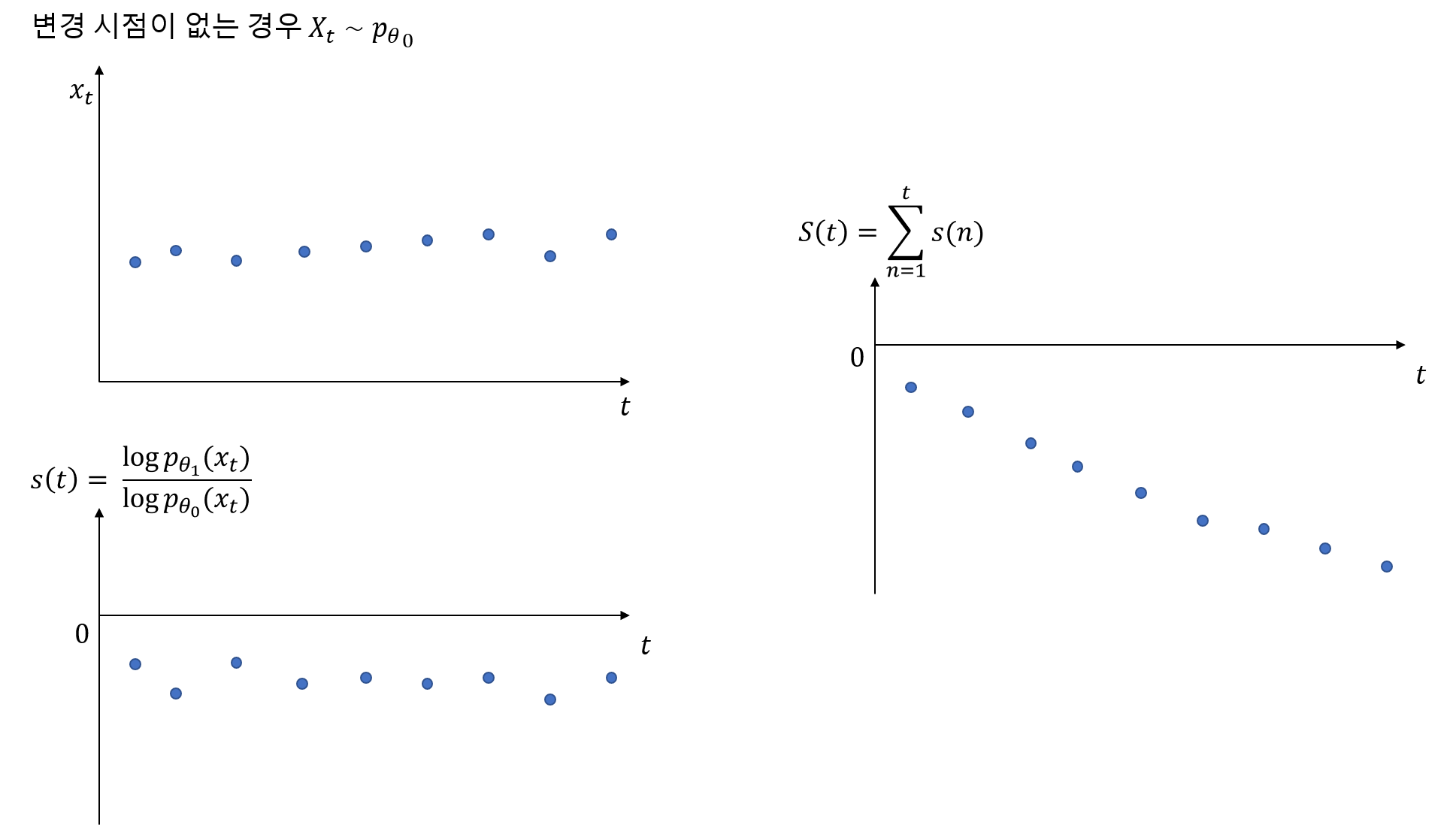
하지만 특정 변경점이 있어서 그 변경점 이후부터는 $X_t$의 확률 밀도 함수가 $p_{\theta_1}(x_t)$로 바뀌므로 개별 로그 우도비 $s(t)$은 양수로 전환되며 이때부터는 $S(t)$가 커지기 시작한다.

하지만 $S(t)$가 작아졌다가 커졌다고 해서 변경점이 있다고 보기에는 무리가 있다. 이러한 현상이 지속되어야 즉, 개별 로그 우도비가 양수인 상태가 어느 정도 지속 되어야 변경점이 있다고 보는 것이 합리적이다. 이는 $S(t)$가 지속적으로 커져야 하는 것을 의미한다. 그렇다면 얼마나 더 커져야 하는가? CUSUM 알고리즘은 $m(t)+h$ 보다 커지는 경우에 변경점이 있다고 알려주는 것이다. 이는 아래와 같은 사실 때문이다.
$$G(t)>h \iff S(t) > m(t)+h\tag{12}$$

여기서 헷갈리지 말아야 할 것은 만약 $S(t) > m(t)+h$를 만족하는 시점 $t$가 $k'$인 경우 $k'$가 변경점이 되는 것은 아니다. (12)가 의미하는 것은 변경점을 구하는 것이 아닌 변경점이 존재하는지를 알려주는 것이다. 변경점은 첫 시점부터 $k'$ 사이에 대하여 $S(t)$가 최소가 되는 지점이 변경지점으로 추정한다.

b. 재귀형(Recursive Form)
CUSUM 알고리즘은 일반형으로도 충분하지만 실시간 업데이트는 일반형만으로는 할 수 없다. 왜냐하면 $m(k)$를 계산하기 위해 처음부터 현재시점까지의 값을 비교한 뒤 최소값을 계산해야 되기 때문이다. 하지만 일반화 우도비의 일반형은 다음과 같이 변형할 수 있다.
$$G(k) = \max \{ G(k-1)+s(k), 0 \}\tag{13}$$
(13)은 이전값에다가 현재 개별 로그 우도비만을 더해주면 되므로 실시간 업데이트가 가능하게 된다.
(13)의 증명
먼저 $G(k-1)+s(k) > 0$이라고 가정하자.
$$\begin{align}G(k-1)+s(k) &= S(k-1)-m(k-1)+s(k) \\ &= S(k)-m(k-1) \\ &= S(k) - m(k) + m(k) - m(k-1) \end{align}$$
이때 $m(k)$의 정의에 의하여 $m(k) \leq m(k-1)$이다. 만약 $m(k) < m(k-1)$이라면 $m(k)=S(k)$이고 이 경우
$$\begin{align}G(k-1)+s(k) &= S(k)-m(k)+m(k) - m(k-1) \\ &= S(k)-S(k)+m(k)-m(k-1) \\ &= m(k)-m(k-1) <0 \end{align}$$
이 되어 앞에서의 가정과 모순된다. 따라서 $m(k) = m(k-1)$이고
$$G(k-1)+s(k) = S(k)-m(k) = G(k)$$
이다.
이번엔 $G(k-1)+s(k) \leq 0$이라고 가정하자. 먼저 $$G(k) = S(k) - m(k) = S(k) - \min_{1\leq t \leq k}S(t) \geq 0$$을 상기하자. $G(k)$를 잘 풀어쓰면
$$\begin{align} G(k) &= S(k) - m(k) \\ &= S(k) - S(k-1)+S(k-1)-m(k-1)+m(k-1)-m(k) \\ &= G(k-1)+s(k) + m(k-1) - m(k) \end{align}$$
만약 $m(k) = m(k-1)$이라면 $G(k)=G(k-1)+s(k)$가 되고 가정한 것과 $G(k)\geq 0$이라는 사실에 의하여
$$0\leq G(k) \leq 0$$
이므로 $G(k) = 0$이 된다.
만약 $m(k) < m(k-1)$이라면 $m(k)=S(k)$가 되어 $$G(k)=S(k)-m(k)=0$$
이 된다. Q.E.D
(4) 정규분포 예제
만약 시계열 $X_t$가 독립인 정규분포를 따른다고 하자. 이 시계열은 특정 시점 $t_c$ 이전에는 평균이 $\mu_0$, 특정 시점 이후에는 기존 평균이 $\mu_1$으로 변경되었다고 해보자. 분산은 모두 $\sigma^2$으로 동일하다고 할 때 확률 밀도 함수는 다음과 같다.
$$\begin{cases} p_{\mu_0}(x_t) &= \frac{1}{\sigma \sqrt{2\pi}} \exp\left\{ - \frac{(x_t - \mu_0)^2}{2\sigma^2}\right \} & \text{ if } t\leq t_c \\ p_{\mu_1}(x_t) &= \frac{1}{\sigma \sqrt{2\pi}} \exp\left\{ - \frac{(x_t - \mu_1)^2}{2\sigma^2}\right \} & \text{ if } t > t_c \end{cases}$$
이제 이를 이용하여 개별 로그 우도비 $s(t)$를 계산하면 다음과 같다.
$$s(t) = \frac{\mu_1-\mu_0}{\sigma^2} \left( x_t - \frac{\mu_1+\mu_2}{2} \right)$$
(5) 고려 사항
a. 모수
앞에 정규분포 예제에서는 모수 $\mu_0, \mu_1$를 안다고 가정했지만 실제로는 알 수 없다. 따라서 데이터를 이용하여 추정해야 한다. 먼저 모수의 관계가 다음과 같다고 해보자.
$$\mu_1 = \mu_0 + \delta $$
이때 $\delta$를 지정해준다고 하면 $\mu_0$를 추정한다면 $\mu_1$은 자동으로 추정할 수 있다. 이때 개별 로그 우도비 $s(t)$에 대하여 $\mu_0, \sigma^2$ 추정치는 다음과 같다.
$$\hat{\mu}_0 = \frac{1}{t}\sum_{k=1}^tx_{k}, \;\;\; \hat{\sigma}^2 = \frac{1}{t-1}\sum_{k=1}^t(x_k-\hat{\mu})^2$$
그리고 개별 로그 우도비 $s(t)$는 다음과 같다.
$$ s(t) = \frac{\delta}{\hat{\sigma}^2}\left ( x_t-\hat{\mu}_0-\frac{\delta}{2} \right) $$
b. $\delta$
$\delta$는 보통 시계열 그림을 그려보고 가장 그럴듯한 값으로 설정하는 것이 효율적이라고 한다.
c. $h$
$h$는 일반화 우도비를 시간에 따라서 그려본 뒤 설정할 수 있다. 이때 $h$를 작게 설정하면 아주 작은 변화를 탐지하며 크게 설정하면 작은 변화는 무시하고 크게 변하는 지점을 설정할 것이다.
(6) CUSUM 알고리즘
이제 모수를 모르는 상황에서 독립인 정규분포를 가정한 CUSUM 알고리즘은 다음과 같다.
CUSUM 알고리즘
(초기화 단계)
$S(0) = G(0) = 0$으로 설정하고 $\delta$와 $h>0$를 지정한다.
$t=1, \ldots, k$까지 아래 단계를 반복한다.
(1단계)
현재 시계열 값 $x_t$, $\hat{\mu}_0, \hat{\sigma}^2$을 계산한다. 이때 $t=1$인 경우 $\hat{\sigma}^2$을 적절한 양수로 설정하거나 처음 $n$개의 샘플을 이용한 추정값으로 대체한다.
(2단계)
다음을 계산한다.
$$\begin{align} s(t) &= \frac{\delta}{\hat{\sigma}^2}\left ( x_t-\hat{\mu}_0-\frac{\delta}{2} \right) \\ S(t) &= S(t-1)+s(t) \\ G(k) &= \max \{ G(k-1)+s(k), 0 \} \end{align} $$
(3단계)
만약 $G(t)>h$이라면 변경점 $t_c$를 다음과 같이 설정한다.
$$\DeclareMathOperator*{\argminA}{arg\,min} t_c = \argminA_{1\leq t' \leq t}S(t')$$
그리고 알고리즘을 종료 또는 리셋한다.
만약 $G(t)\leq h$이면
$t = t+1$로 설정하고 (1단계)로 돌아간다.
위의 알고리즘은 한 방향 변경지점을 찾는다는 것을 알 수 있다. 즉, $\mu_0$를 기준으로 커지는 지점만 찾거나 작아지는 지점만을 찾게 되는 한 방향 변경 지점 탐지 알고리즘인 것이다. 이에 따라 위 알고리즘을 One-sided CUSUM 알고리즘이라고도 한다. 이제 $\mu_0$를 기준으로 커지는 변경점과 작아지는 변경점 모두를 찾을 수 있는 Two-sided CUSUM 알고리즘을 소개한다. Two-sided CUSUM 알고리즘은 One-sided CUSUM 알고리즘을 두 방향으로 하는 것이다.
예를 들어 $\mu_1 > \mu_0$라면 $\mu_1 = \mu_0+|\delta|$로 표현할 수 있고 $\mu_1< \mu_0$라면 $\mu_1=\mu_0-|\delta|$라 할 수 있다. 먼저 $\mu_1 = \mu_0+|\delta|$라고 가정하고 정규 분포를 가정한 개별 로그 우도비는 다음과 같다.
$$s^i(t) = \frac{|\delta|}{\hat{\sigma}^2}\left ( x_t - \mu_0 - \frac{|\delta|}{2} \right )$$
그리고 $\mu_1=\mu_0-|\delta|$인 경우 개별 로그 우도비는 다음과 같다.
$$s^d(t) = -\frac{|\delta|}{\hat{\sigma}^2} \left ( x_t-\mu_0+\frac{|\delta|}{2} \right )$$
이렇게 구한 $s^i(t), s^d(t)$를 각각 CUSUM 알고리즘에 적용하면 된다. Two-sided CUSUM 알고리즘은 다음과 같다.
Two-sided CUSUM 알고리즘
(초기화 단계)
$S^i(0) = G^i(0) = S^d(0) = G^d(0) 0$으로 설정하고 $\delta$와 $h>0$를 지정한다.
$t=1, \ldots, k$까지 아래 단계를 반복한다.
(1단계)
현재 시계열 값 $x_t$, $\hat{\mu}_0, \hat{\sigma}^2$을 계산한다. 이때 $t=1$인 경우 $\hat{\sigma}^2$을 적절한 양수로 설정하거나 처음 $n$개의 샘플을 이용한 추정값으로 대체한다.
(2단계)
다음을 계산한다.
$$\begin{align} s^i(t) &= \frac{|\delta|}{\hat{\sigma}^2}\left ( x_t-\hat{\mu}_0-\frac{|\delta|}{2} \right) \\ s^d(t) &= -\frac{|\delta|}{\hat{\sigma}^2}\left ( x_t-\hat{\mu}_0+\frac{|\delta|}{2} \right) \\ S^i(t) &= S^i(t-1)+s^i(t), \;\; S^d(t) = S^d(t-1)+s^d(t) \\ G^i(k) &= \max \{ G^i(k-1)+s^i(k), 0 \}, \;\; G^d(k) = \max \{ G^d(k-1)+s^d(k), 0 \}, \end{align} $$
(3단계)
만약 $G^i(t)>h$이라면 변경점 $t_c$를 다음과 같이 설정한다.
$$\DeclareMathOperator*{\argminA}{arg\,min} t_c = \argminA_{1\leq t' \leq t}S^i(t')$$
또는 $G^d(t)>h$이라면 변경점 $t_c$를 다음과 같이 설정한다.
$$\DeclareMathOperator*{\argminA}{arg\,min} t_c = \argminA_{1\leq t' \leq t}S^d(t')$$
그리고 알고리즘을 종료 또는 리셋한다.
위 두 조건을 만족하지 않는다면
$t = t+1$로 설정하고 (1단계)로 돌아간다.
만약 변경점을 여러 개 찾고 싶다면 적당한 주어진 시계열을 적당한 구간으로 쪼갠다음 각 구간별로 CUSUM 알고리즘을 적용하면 된다.
2. 파이썬(Python) 구현
이제 앞에서 배운 내용을 바탕으로 정규 분포 CUSUM 알고리즘을 구현해 보자. 아래 코드는 One-sided CUSUM 알고리즘을 수행하는 클래스이다.
class oneSidedCUSUM:
def __init__(self, delta, h=None):
self.delta = delta
self.h = h
self.G_list = None
self.S_list = None
self.G_min_idx = None
self.cpd_idx = None
def mean(self, x, k):
if k == 0:
return x[k]
return np.mean(x[:k])
def var(self, x, k):
return np.var(x[:k])
def get_s_unknown(self, x, k, mu1, delta, sigma):
temp = (delta/sigma)*(x[k] - mu1 - 0.5*delta)
return temp
def find_change_point(self, signal):
G_list = []
S_list = []
G = 0
S = 0
delta = self.delta
for k in range(len(signal)):
if k == 0: ## 초기값
sigma = 1
mu1 = 0
else: ## 평균과 분산 추정
mu1 = self.mean(signal, k+1)
sigma = self.var(signal, k+1)
s = self.get_s_unknown(signal, k, mu1, delta, sigma) ## 개별 로그 우도비
G = np.max([G+s, 0]) ## 일반화 우도비
S = S + s ## 개별 로그 우도비 누적합
G_list.append(G)
S_list.append(S)
self.G_list = G_list
self.S_list = S_list
if self.h is not None:
## 일반화 우도비가 h를 넘어가는 인덱스
self.G_min_idx = np.min(np.where(np.array(G_list) > self.h)[0])
target_S_list = S_list[:self.G_min_idx] ## 인덱스 범위 제한
self.cpd_idx = target_S_list.index(min(target_S_list)) ## 개별 로그 우도비 누적합이 최소가 되는 인덱스
return self
이 클래스는 $delta, h$ 값을 초기 인자로 받는다. 그리고 특정 구간까지의 평균과 분산을 계산하는 mean, var 메서드를 구현하고 개별 로그 우도비를 계산하는 get_s_unknown 메서드로 구현했다.
그리고 find_change_point 메서드가 실제로 변경지점을 찾아준다. 이 메서드는 주어진 시계열을 하나씩 돌면서 개별 로그 우도비를 계산하고 일반화 우도비와 누적합을 계산한다(line 28~39). 그리고 일반화 우도비가 $h$를 넘어가는 최초 인덱스를 계산하고(line 45) 누적합이 담겨있는 리스트를 앞에서 구한 인덱스로 범위를 제한한 뒤 최소가 되는 인덱스를 변경점으로 선택하게 된다(line 46~47).
모의실험 (1)
이제 모의실험을 해보자. 먼저 아래와 같이 1200개의 랜덤 난수를 생성하는데 1000개는 표준 정규분포를 따르고 뒤에 200개는 평균과 분산이 1인 정규분포를 따르는 난수로 구성했다. 이를 시각화하면 다음과 같다.
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['axes.unicode_minus'] = False
np.random.seed(100)
before_size = 1000
after_size = 200
time_series = np.concatenate([np.random.randn(before_size), np.random.randn(after_size)+1])
fig = plt.figure(figsize=(15, 6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(range(len(time_series)), time_series)
plt.show()

만약 변경 탐지 알고리즘이 정확하다면 999번째 인덱스를 찾아야 할 것이다. 먼저 $\delta=1.5$가 적당해 보였다. 그리고 일반화 우도비의 경계값 $h$를 선정하기 위해 일반화 우도비를 시간에 따라 그려보았다.
delta = 1.5
osc = oneSidedCUSUM(delta=delta, h=None).find_change_point(time_series)
fig = plt.figure(figsize=(15, 6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(range(len(time_series)), osc.G_list)
plt.show()
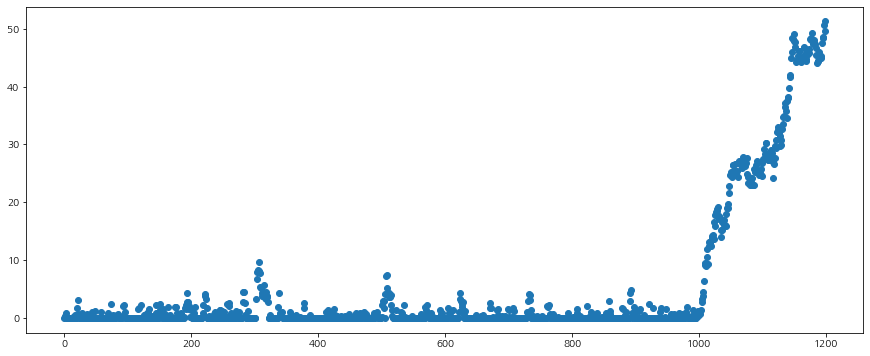
보아하니 $h$는 20 정도면 될듯하다(사실 모의실험에서 사용한 데이터는 내가 만들어 낸 것이니까 실제로 쉽게 결정할 수 있는 것이지 실제 문제에서는 훨씬 어렵다). 그래서 $h=20$으로 설정하고 변경지점을 찾아보자.
delta = 1.5
osc = oneSidedCUSUM(delta=delta, h=20).find_change_point(time_series)
print(osc.cpd_idx)
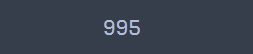
One-sided CUSUM 알고리즘을 통해 찾은 변경점은 995이다. 실제 변경점 999와 거의 흡사하다. 이번엔 시계열, 일반화 우도비, 누적합을 그려보았다. 이때 알고리즘을 통해 찾은 변경점과 일반화 우도비가 경계값 $h$를 넘어가는 지점과 누적합이 최소가 되는 지점을 표시했다.

시계열이 정규 분포를 따르되 평균이 한쪽 방향으로 달라지는 상황이라면 One-sided CUSUM 알고리즘은 꽤나 좋아 보인다.
이번엔 Two-sided CUSUM 알고리즘을 구현해 보자. 아래 코드는 Two-sided CUSUM 알고리즘을 수행하는 클래스이다. 원리는 One-sided CUSUM 알고리즘과 유사하므로 설명은 생략한다.
class twoSidedCUSUM:
def __init__(self, delta, h=None):
self.delta = delta
self.h = h
self.G_increase_list = None
self.S_increase_list = None
self.G_decrease_list = None
self.S_decrease_list = None
self.G_increase_min_idx = None
self.increase_cpd_idx = None
self.G_decrease_min_idx = None
self.decrease_cpd_idx = None
def mean(self, x, k):
if k == 0:
return x[k]
return np.mean(x[:k])
def var(self, x, k):
return np.var(x[:k])
def get_s_unknown(self, x, k, mu1, delta, sigma, sign):
delta = abs(self.delta)
if sign == 1:
temp = (delta/sigma)*(x[k] - mu1 - 0.5*delta)
else:
temp = -(delta/sigma)*(x[k] - mu1 + 0.5*delta)
return temp
def find_change_point(self, signal):
G_increase_list = []
S_increase_list = []
G_decrease_list = []
S_decrease_list = []
G_i = 0
S_i = 0
G_d = 0
S_d = 0
delta = abs(self.delta)
for k in range(len(signal)):
if k == 0:
sigma = 1
mu1 = 0
else:
mu1 = self.mean(signal, k+1)
sigma = self.var(signal, k+1)
s_i = self.get_s_unknown(signal, k, mu1, delta, sigma, 1)
s_d = self.get_s_unknown(signal, k, mu1, delta, sigma, -1)
G_i = np.max([G_i+s_i, 0])
G_d = np.max([G_d+s_d, 0])
S_i += s_i
S_d += s_d
G_increase_list.append(G_i)
S_increase_list.append(S_i)
G_decrease_list.append(G_d)
S_decrease_list.append(S_d)
self.G_increase_list = G_increase_list
self.S_increase_list = S_increase_list
self.G_decrease_list = G_decrease_list
self.S_decrease_list = S_decrease_list
if self.h is not None:
self.G_increase_min_idx = np.min(np.where(np.array(G_increase_list) > self.h)[0])
target_S_increase_list = S_increase_list[:self.G_increase_min_idx]
self.increase_cpd_idx = target_S_increase_list.index(min(target_S_increase_list))
self.G_decrease_min_idx = np.min(np.where(np.array(G_decrease_list) > self.h)[0])
target_S_decrease_list = S_decrease_list[:self.G_decrease_min_idx]
self.decrease_cpd_idx = target_S_decrease_list.index(min(target_S_decrease_list))
return self
모의실험 (2)
이번에는 변경점을 두 개가 있는 난수 시계열을 만들었다. 여기서는 499, 999번째 인덱스에서 변경이 일어난다.
np.random.seed(100)
size = 500
time_series = np.concatenate([np.random.randn(size), np.random.randn(size)+1, np.random.randn(size)-1])
fig = plt.figure(figsize=(15, 6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(range(len(time_series)), time_series)
plt.show()

앞에 실험과 마찬가지로 $\delta = 1.5, h=20$으로 설정하고 Two-sided CUSUM 알고리즘을 통해 변경점을 찾아보자.
delta = 1.5
h = 20
tsc = twoSidedCUSUM(delta=delta, h=h).find_change_point(time_series)
print(tsc.increase_cpd_idx)
print(tsc.decrease_cpd_idx)

매우 정확한 변경점을 찾았다. 이번엔 난수 시계열과 변경점을 표시한 결과를 시각화해 보자.
fig = plt.figure(figsize=(15, 6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.scatter(range(len(time_series)), time_series)
ax.axvline(tsc.increase_cpd_idx, linestyle='--', color='red')
ax.axvline(tsc.decrease_cpd_idx, linestyle='--', color='red')
plt.show()

3. 장단점
CUSUM 알고리즘의 장단점은 다음과 같다.
- 장점 -
a. 우도 함수가 있기만 하면 사용할 수 있는 알고리즘이다.
b. 알고리즘이 직관적이며 실제 코딩으로 구현하기가 쉽다.
c. 실제로 가정한 우도 함수(확률 분포)가 맞다면 변경점을 잘 찾는다.
d. 재귀형을 사용하면 실시간으로 변경 여부를 탐지할 수 있다.
- 단점 -
a. $\delta, h$를 잘 선택해야 한다.
b. 실제로 시계열이 생성된 확률 분포를 알기 어렵다.
c. 샘플이 많아지면 그만큼 계산량도 많아진다.
실제로 시계열 데이터에서 변경 탐지 문제는 정말 많은 곳에서 풀어야할 분야이며 변경 탐지 알고리즘이 많이 활용되는 것 같아 관련 알고리즘을 공부하고 알아두면 여러모로 쓸모가 있다. 이번 포스팅에서는 기본적이지만 많은 원리를 갖고 있는 CUSUM 알고리즘에 대해서 공부해보았는데 원리를 이해하니 재밌었다. 다른 변경 탐지 알고리즘도 공부해서 포스팅해보려고 한다.
- 참고 자료 -
P Granjon - The CuSum algorithm
Bassevile - Detection of abrupt changes
'통계 > 시계열 모형' 카테고리의 다른 글
| [시계열 분석] 10. Phillips-Perron Test(검정) with Python (422) | 2022.04.18 |
|---|---|
| [시계열 분석] 9. (Augmented) Dickey-Fuller Test(검정) with Python (419) | 2022.04.14 |
| [시계열 분석] 8. Random Walk와 단위근 검정(Unit Root Test)에 대해서 알아보자. (839) | 2021.09.24 |
| [시계열 분석] 7. ARMA 모형에 대해서 알아보자 with Python (803) | 2021.09.18 |
| [시계열 분석] 6. 이동 평균 모형(Moving Average Model) 적합하기 with Python (809) | 2021.08.20 |





댓글