이번 포스팅은 단위근 검정의 한 방법으로 (Augmented) Dickey-Fuller(ADF)와 쌍벽을 이루는 Phillips-Perron Test(검정)에 대해서 알아본다. 그리고 파이썬을 이용하여 샘플 데이터를 통한 예제도 알아보고자 한다.
이번 포스팅에서 다룰 내용은 다음과 같다.
2. Python 예제 - Phillips-Perron Test(검정)
본 포스팅에서는 수식을 포함하고 있습니다.
티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니
PC 웹 브라우저 또는 모바일 웹 브라우저에서 보시기 바랍니다.
1. Phillips-Perron Test(검정)
1.1 정의
다음과 같은 시계열이 있다고 하자.
$$\Delta X_t = c_t + (\rho - 1)X_{t-1} + W_t, t=1,2, \ldots, T$$
$W_t$는 보통은 백색잡음이지만 꼭 그럴 필요 없다. 여기서 $W_t$는 등분산성은 만족하지 않을 수도 있고 약한 자기 상관성을 가질 수도 있다. 그리고 $c_t$는 다음과 같이 3종류 형태가 있는 트렌드 함수이다.
$$\begin{align} (A) \text{ } c_t &= 0 \text{ no time trend, no intercept} \\ (B) \text{ } c_t &= a \text{ intercept but no time trend} \\ (C) \text{ }c_t &= a_0+a_1t \text{ intercept with time trend} \end{align}$$
Phillips-Perron Test(검정)의 귀무가설과 대립 가설은 다음과 같다.
$$H_0 : \rho = 1 \text{ vs } H_1 : \rho < 1$$
귀무가설은 해당 시계열이 단위근이 있다는 것을 의미하며 이는 비정상 시계열임을 뜻한다. 그리고 대립 가설은 부분 정상성(Local Stationary)을 만족하는 시계열이다.
Phillips-Perron Test(검정)은 최소 제곱법을 이용하여 추정한 $\hat{\rho}$과 그에 대응하는 $t$ 통계량 $$\tau = \frac{\hat{\rho}-1}{SE(\hat{\rho})}$$
을 이용하여 검정한다. 하지만 $\hat{\rho}$과 $\tau$를 바로 이용하는 것이 아니라 $Z$ 통계량이라는 것을 사용한 통계량을 검정 통계량으로 사용한다. 그 이유를 설명하기 위하여 다음을 정의한다.
$$\sigma^2 = \lim_{t\rightarrow\infty}E(T^{-1}S_T^2), S_t = \sum_{j=1}^tW_j\tag{1.1}$$
$$\sigma_W^2 = \lim_{t\rightarrow\infty}E(W_t^2)\tag{1.2}$$
$Z$ 통계량을 사용한 이유를 알아보자. 기존 $\hat{\rho}$과 $\tau$의 기각값을 계산하기 위하여 귀무 가설이 참일 때 극한 분포를 계산해야한다. 근데 이 극한 분포가 nuisance 모수($\sigma^2, \sigma_W^2$)에 의존하게 된다. 이렇게 되면 안그래도 샘플이 큰 경우에 그나마 정확한 기각값을 구할 수 있는데 nuisance 모수가 포함되어 있어 이를 추정해서 플러그인(Plug-In)하면 기각값의 정확성이 떨어지게 된다. 또한 nuisance 모수가 있으면 기각값의 테이블을 만들수 없다. 왜냐하면 nuisance 모수의 추정값을 미리 알 수 없기 때문이다. 이러한 연유로 Phillips와 Perron은 이러한 nuisance 모수에 의존하지 않는 변환을 고안하여 $Z$ 통계량을 만든 것이다. 이게 Phillips-Perron Test(검정)의 핵심이다.
1.2 검정 방법
Phillips-Perron 검정 방법은 다음과 같다.
1) Phillips-Perron 검정에서 검정 통계량을 계산한다.
검정 통계량은 다음과 같다.
$$Z_{\hat{\rho}} = T(\hat{\rho}-1) - \frac{1}{2}\frac{T^2 \cdot SE(\hat{\rho})}{\hat{s}^2}(\hat{\sigma}^2-\hat{\sigma}_W^2)\tag{1.3}$$
$$Z_{\tau} = \left(\frac{\hat{\sigma}_W^2}{\hat{\sigma}^2}\right)^{1/2}\tau- \frac{T(\hat{\sigma}^2-\hat{\sigma}_W^2)SE(\hat{\rho})}{2(\hat{\sigma}^2\hat{s}^2)^{1/2}} \tag{1.4}$$
여기서 $\hat{\sigma}^2, \hat{\sigma}_W^2$은 식 (1.1), (1.2)에서 $\sigma^2, \sigma_W^2$의 추정량으로 다음과 같이 계산한다.
$$\hat{\sigma}^2 = T^{-1}\sum_{t=1}^T\hat{w}_t^2+2T^{-1}\sum_{s=1}^la_{sl}\sum_{t=s+1}^T\hat{w}_t\hat{w}_s\tag{1.5}$$
이때 $\hat{w}_t, t=1, 2, \ldots, T$는 회귀 모형으로 얻어진 잔차이며
$$a_{sl} = 1-s/(l+1)$$
이다. 그리고 $\hat{\sigma}_W^2 = \sum_{t=1}^T\hat{w}_t^2$, $\hat{s}^2$은 평균오차제곱(MSE)이다(자유도를 분모로 한다).
여기서 궁금증이 생긴다. 왜 통계량 두 개를 만든 걸까?
논문을 봤는데 정확한 이유는 찾지 못했으나 개인적인 생각으로 기존 단위근 검정(Said, Dickey) 보다 좋다는 것을 실험하기 위하여 하나보다는 두 개가 나으니까 그런 것 같다. 실제로 Phillips와 Perron 논문에서 어느 하나가 안 좋으면 다른 하나는 좋다는 결과를 보여준다.
2) 기각 여부 결정
이제 검정 통계량을 계산했으면 테이블을 이용하여 (A)~(C)에 대응하는 기각값을 선택한다.
테이블은 다음과 같다.
기각값을 찾았으면 검정 통계량과 비교한다. 이때 검정 통계량이 기각값보다 작으면 귀무가설을 기각한다.
1.3 장단점
Phillips-Perron의 장점은 다음과 같다.
1) 장점
a. 좀 더 폭넓은 오차항 시계열을 다룰 수 있다.
Phillips-Perron 검정은 앞서 이야기했듯이 오차항은 반드시 백색 잡음 또는 정상성을 가질 필요는 없으며 자기 상관성을 갖거나 시간에 따른 등분산성을 만족하지 않아도 사용할 수 있는 검정방법이다. 또한 등분산성을 나타내는 수학적인 형태의 Robust 한 방법이다.
b. 자기 회귀 차수를 신경 쓰지 않아도 된다.
Phillips-Perron 검정은 Augmented Dickey Fuller과 달리 자기 회귀 차수를 신경쓰지 않아도 된다.
2) 단점
a. 자기 상관 차수를 정해야 한다.
Phillips-Perron 검정은 $\sigma^2$ 추정 시 자기 상관 차수 $l$을 정해줘야 한다. 주로
$$l \approx 4\left(\frac{T}{100} \right)^{1/4}$$
또는
$$l \approx 12\left(\frac{T}{100} \right)^{1/4}$$
를 주로 쓴다고 한다.
b. 소표본일 경우의 검정의 정확성이 매우 안 좋다.
소표본일 경우 검정의 정확성이 Augmented Dickey-Fuller 검정보다 매우 안 좋다고 한다.
2. Python 예제 - Phillips-Perron Test(검정)
이번엔 파이썬을 이용하여 Phillips-Perron 검정을 구현해보자.
2.1 함수 만들어보기
먼저 Phillips-Perron 검정을 수행하는 함수를 만들어보자. 여기서 만든 함수는 R 패키지 aTSA의 pp.test 함수를 참고했다.
먼저 필요한 모듈을 임포트한다.
import pandas as pd
import numpy as np
import math
import statsmodels.api as sm
import warnings
warnings.filterwarnings('ignore')
먼저 시계열 $X_t$ $X_{t-j}, j=1, 2, \ldots$를 한 매트릭스에 모아주는 embed 함수를 먼저 만들었다.
def embed(z, lags):
res = []
for i in range(lags):
temp_z = np.expand_dims(z[lags-1-i:len(z)-i], axis=1)
res.append(temp_z)
res = np.concatenate(res, axis=1)
return res
이제 주인공이 나올 시간이다. Phillips-Perron 검정을 수행하는 함수다. 먼저 검정 통계량 $Z_{\hat{\rho}}, Z_\tau$를 계산하는 stat 함수, 테이블을 참조하여 주어진 샘플 수에 대하여 적절히 보간법(Interpolation)을 적용하여 p value를 계산하는 get_pval 함수를 내부에서 정의한다.
그러고 나서 (A)~(C)인 경우의 회귀 모형을 적합하고 이를 이용하여 각 경우의 검정 통계량과 p value를 계산하고 그 결과를 튜플 형식으로 반환한다.
def phillips_perron_test(x, statistic_type = 'z_rho', lag_short = True):
def stat(model, m):
idx = 1
if m > 1:
idx = 2
res1 = model.resid
rho_hat = model.params[idx-1]
sig_hat = model.bse[idx-1]
s2 = np.sum(np.square(res1))/(n-m)
gamma = []
for i in range(1, q+2):
u = embed(res1, i)
gamma_val = np.sum(u[:, 0]*u[:, i-1])/n
gamma.append(gamma_val)
lambda2 = gamma[0]+2*np.sum((1-np.array(range(1, q+1))/(q+1))*gamma[1:])
z_r = n*(rho_hat-1) - ((n**2)*(sig_hat**2)/s2)*(lambda2-gamma[0])/2
z_t = np.sqrt(gamma[0]/lambda2)*(rho_hat-1)/sig_hat-\
(lambda2-gamma[0])*n*sig_hat/(2*np.sqrt(lambda2*s2))
return (z_r, z_t)
def get_pval(table, stat):
from scipy import interpolate
table = np.array(table)
ncol = table.shape[1]
size = (25, 50, 100, 250, 500, 1000)
percnt = (0.01, 0.025, 0.05, 0.1, 0.5, 0.9, 0.95, 0.975, 0.99)
interpol_size = []
for j in range(ncol):
f_temp = interpolate.interp1d(size, table[:, j], fill_value='extrapolate')
interpol_size.append(f_temp(n).item())
f = interpolate.interp1d(interpol_size, percnt, fill_value='extrapolate')
return f(stat).item()
assert statistic_type in ['z_rho', 'z_tau']
z = embed(x, 2)
yt = z[:,0]
yt1 = z[:,1]
n = len(yt)
assert n >= 1
t = range(1, n+1)
lag = 4
if not lag_short:
lag = 12
q = math.ceil(lag*(n/100)**(0.25))
table_r1 = ((-11.8, -9.3, -7.3, -5.3, -0.82, 1.01, 1.41, 1.78, 2.28),
(-12.8, -9.9, -7.7, -5.5, -0.84, 0.97, 1.34, 1.69, 2.16),
(-13.3, -10.2, -7.9, -5.6, -0.85, 0.95, 1.31, 1.65, 2.09),
(-13.6, -10.4, -8, -5.7, -0.86, 0.94, 1.29, 1.62, 2.05),
(-13.7, -10.4, -8, -5.7, -0.86, 0.93, 1.29, 1.61, 2.04),
(-13.7, -10.5, -8.1, -5.7, -0.86, 0.93, 1.28, 1.6, 2.03))
table_r2 = ((-17.2, -14.6, -12.5, -10.2, -4.22, -0.76, 0, 0.64, 1.39),
(-18.9, -15.7, -13.3, -10.7, -4.29, -0.81, -0.07, 0.53, 1.22),
(-19.8, -16.3, -13.7, -11, -4.32, -0.83, -0.11, 0.47, 1.13),
(-20.3, -16.7, -13.9, -11.1, -4.34, -0.84, -0.13, 0.44, 1.08),
(-20.5, -16.8, -14, -11.2, -4.35, -0.85, -0.14, 0.42, 1.07),
(-20.6, -16.9, -14.1, -11.3, -4.36, -0.85, -0.14, 0.41, 1.05))
table_r3 = ((-22.5, -20, -17.9, -15.6, -8.49, -3.65, -2.51, -1.53, -0.46),
(-25.8, -22.4, -19.7, -16.8, -8.8, -3.71, -2.6, -1.67, -0.67),
(-27.4, -23.7, -20.6, -17.5, -8.96, -3.74, -2.63, -1.74, -0.76),
(-28.5, -24.4, -21.3, -17.9, -9.05, -3.76, -2.65, -1.79, -0.83),
(-28.9, -24.7, -21.5, -18.1, -9.08, -3.76, -2.66, -1.8, -0.86),
(-29.4, -25, -21.7, -18.3, -9.11, -3.77, -2.67, -1.81, -0.88))
table_t1 = ((-2.65, -2.26, -1.95, -1.6, -0.47, 0.92, 1.33, 1.7, 2.15),
(-2.62, -2.25, -1.95, -1.61, -0.49, 0.91, 1.31, 1.66, 2.08),
(-2.6, -2.24, -1.95, -1.61, -0.5, 0.9, 1.29, 1.64, 2.04),
(-2.58, -2.24, -1.95, -1.62, -0.5, 0.89, 1.28, 1.63, 2.02),
(-2.58, -2.23, -1.95, -1.62, -0.5, 0.89, 1.28, 1.62, 2.01),
(-2.58, -2.23, -1.95, -1.62, -0.51, 0.89, 1.28, 1.62, 2.01))
table_t2 = ((-3.75, -3.33, -2.99, -2.64, -1.53, -0.37, 0, 0.34, 0.71),
(-3.59, -3.23, -2.93, -2.6, -1.55, -0.41, -0.04, 0.28, 0.66),
(-3.5, -3.17, -2.9, -2.59, -1.56, -0.42, -0.06, 0.26, 0.63),
(-3.45, -3.14, -2.88, -2.58, -1.56, -0.42, -0.07, 0.24, 0.62),
(-3.44, -3.13, -2.87, -2.57, -1.57, -0.44, -0.07, 0.24, 0.61),
(-3.42, -3.12, -2.86, -2.57, -1.57, -0.44, -0.08, 0.23, 0.6))
table_t3 = ((-4.38, -3.95, -3.6, -3.24, -2.14, -1.14, -0.81, -0.5, -0.15),
(-4.16, -3.8, -3.5, -3.18, -2.16, -1.19, -0.87, -0.58, -0.24),
(-4.05, -3.73, -3.45, -3.15, -2.17, -1.22, -0.9, -0.62, -0.28),
(-3.98, -3.69, -3.42, -3.13, -2.18, -1.23, -0.92, -0.64, -0.31),
(-3.97, -3.67, -3.42, -3.13, -2.18, -1.24, -0.93, -0.65, -0.32),
(-3.96, -3.67, -3.41, -3.13, -2.18, -1.25, -0.94, -0.66, -0.32))
X = np.expand_dims(yt1, axis=1)
model1 = sm.OLS(yt, X).fit()
X = sm.add_constant(X)
model2 = sm.OLS(yt, X).fit()
X = np.concatenate([X, np.expand_dims(t, axis=1)], axis=1)
model3 = sm.OLS(yt, X).fit()
stats = np.array([np.array(stat(model1, 1)), np.array(stat(model2, 2)), np.array(stat(model3, 3))])
pvalue_delta = [get_pval(table_r1, stats[0,0]), get_pval(table_r2, stats[1,0]),
get_pval(table_r3, stats[2,0])]
pvalue_t_delta = [get_pval(table_t1, stats[0,1]), get_pval(table_t2, stats[1,1]),
get_pval(table_t3, stats[2,1])]
if statistic_type == 'z_rho':
statistic = stats[:, 0]
p_value = pvalue_delta
else:
statistic = stats[:, 1]
p_value = pvalue_t_delta
return (q, statistic_type, list(statistic), p_value)
이제 샘플 데이터에 대하여 Phillips-Perron 검정을 해보자.
x = [3, 4, 4, 5, 6, 7, 6, 6, 7, 8, 9, 12, 10]
시계열을 그려보자.
import matplotlib.pyplot as plt
fig = plt.figure(figsize=(7,4))
fig.set_facecolor('white')
plt.plot(range(len(x)), x, marker='o')
plt.show()
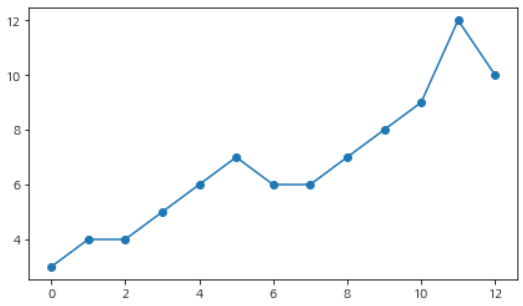
딱 봐도 정상성을 갖는 시계열은 아니다. 먼저 $Z_\tau$ 검정 통계량을 이용한 Phillips-Perron 검정을 해보자.
results = phillips_perron_test(x, statistic_type='z_tau', lag_short=False)
print("Phillips-Perron Unit Root Test")
print("alternative: stationary")
lag = results[0]
statistic_type = results[1]
text_dict = {
0:"Type 1: no drift no trend",
1:"Type 2: with drift no trend",
2:"Type 3: with drift and trend"
}
for i, (statistic, pval) in enumerate(zip(results[2], results[3])):
print(text_dict[i])
print('lag : {0}, {1} : {2}, p_value : {3}'.format(lag, statistic_type, statistic, pval) )
모든 경우에 대해서 p value가 0.05보다 크다. 따라서 귀무가설은 기각되며 해당 시계열은 단위근을 갖는다고 할 수 있다.
이번엔 $Z_{\hat{\rho}}$를 검정 통계량으로 하는 Phillips-Perron 검정을 수행해보자.
results = phillips_perron_test(x, statistic_type='z_rho', lag_short=False)
print("Phillips-Perron Unit Root Test")
print("alternative: stationary")
lag = results[0]
statistic_type = results[1]
text_dict = {
0:"Type 1: no drift no trend",
1:"Type 2: with drift no trend",
2:"Type 3: with drift and trend"
}
for i, (statistic, pval) in enumerate(zip(results[2], results[3])):
print(text_dict[i])
print('lag : {0}, {1} : {2}, p_value : {3}'.format(lag, statistic_type, statistic, pval) )
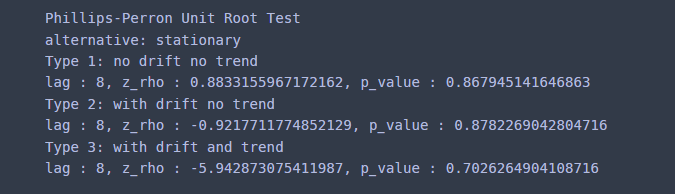
마찬가지로 (A)~(C) 모든 경우에 대하여 p value가 0.05보다 크므로 귀무가설은 기각된다. 따라서 해당 시계열은 단위근을 갖는다고 할 수 있다. 앞선 결과의 차이점은 p value가 더 보수적으로 잡혔다는 것이다.
2.2 arch 패키지 이용하기
이번엔 시계열 분석을 위한 arch 패키지를 이용하여 Phillips-Perron 검정을 수행해보자.
사용 방법은 쉽다. PhillipsPerron 클래스를 생성하고 trend 인자에 사전에 정해진 문자열을 입력한다. 여기에는 'nc'(No Trend, No Constant), 'c'(Only Constant), 'ct'(Trend and Constant)를 입력할 수 있다. 그리고 검정 통계량을 $Z_\tau$로 할지 $ Z_{\hat{\rho}}$로 할지는 test_type인자를 이용하여 설정한다.
먼저 $Z_\tau$ 검정 통계량을 이용한 Phillips-Perron 검정을 해보자.
from arch.unitroot import PhillipsPerron
for tt in ['nc','c','ct']:
pp = PhillipsPerron(x, trend=tt, test_type='tau')
print(pp.summary().as_text())
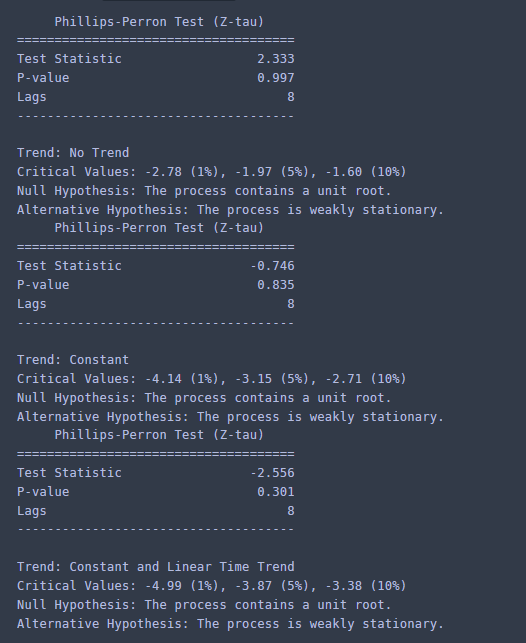
결과를 보면 검정 통계량이 앞서서 직접 구현했던 것과 동일하였다. 하지만 p value가 조금 달랐는데 이는 샘플 사이즈에 따른 보간법(Interpolation) 적용 방식이 달라서 그런 것 같다. 이 경우 (A)~(B) 모든 경우에 대하여 p value가 0.05보다 크므로 귀무가설은 기각된다.
이번엔 $Z_{\hat{\rho}}$를 검정 통계량으로 하는Phillips-Perron 검정을 수행해보자.
for tt in ['nc','c','ct']:
pp = PhillipsPerron(x, trend=tt, test_type='rho')
print(pp.summary().as_text())
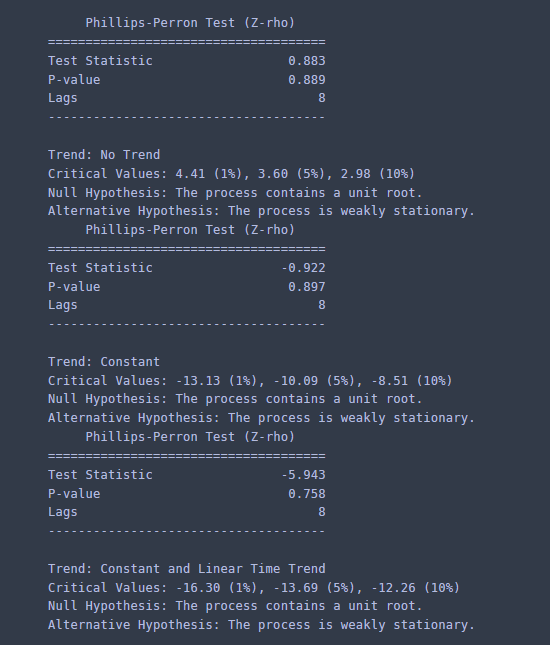
이 경우에도 (A)~(B) 모든 경우에 대하여 p value가 0.05보다 크므로 귀무가설은 기각된다. 따라서 해당 시계열에 단위근이 존재한다고 할 수 있다.
참고자료
Peter C, B. Phillips, Pierre Perron - Testing for a Unit Root in Time Series Regression
https://faculty.washington.edu/ezivot/econ584/notes/unitroot.pdf
https://en.wikipedia.org/wiki/Phillips%E2%80%93Perron_test
'통계 > 시계열 모형' 카테고리의 다른 글
| [Change Point Detection] 1. CUSUM(Cumulative Sum) 알고리즘에 대해서 알아보자 with Python (3) | 2023.01.02 |
|---|---|
| [시계열 분석] 9. (Augmented) Dickey-Fuller Test(검정) with Python (419) | 2022.04.14 |
| [시계열 분석] 8. Random Walk와 단위근 검정(Unit Root Test)에 대해서 알아보자. (839) | 2021.09.24 |
| [시계열 분석] 7. ARMA 모형에 대해서 알아보자 with Python (803) | 2021.09.18 |
| [시계열 분석] 6. 이동 평균 모형(Moving Average Model) 적합하기 with Python (809) | 2021.08.20 |
댓글