비선형 모형에서의 변수 선택 방법론을 제시한 Feature Selection using Stochastic Gates 논문을 읽고 정리해본다.
- 목차 -
1. Introduction
2. Problem Setup and Background
3. Proposed Method
4. Connection to Mutual Information
5. Related Work
6. Experiments
7. Cox Proportional Hazard Models for Survival Analysis
8. Evaluating Stochastic Regularization Schemes
9. Feature Selection with Correlations
10. Conclusion
1. Introduction
머신 러닝에서 변수의 부분 집합을 잘 고르는 것은 매우 중요하다. 왜냐하면 변수 부분집합을 잘 고른다면 해석력과 계산 속도가 올라가고 메모리 공간은 아낄 수 있으며 일반화가 잘될 수 있기 때문이다.
변수 선택은 크게 3가지로 분류된다. Filter 방법, Wrapper 방법 그리고 Embedded 방법이 그것이다.
Filter 방법은 모형 학습 전에 사전에 통계적인 방법으로 변수를 걸러내는 것이고, Wrapper 방법은 특정 변수 집합에 대해서 매번 모형의 재학습 과정을 거쳐서 모형의 성능 지표를 통하여 변수 집합을 선택하는 것이다. 마지막으로 Embedded 방법은 변수 선택과 학습을 동시에 해주는 방법이다. Embedded 방법의 대표적인 예는 LASSO가 있는데 LASSO를 비선형 모형으로 예를 들면 인공신경망으로 확장하면 잘 작동되지도 않고 Sparse 한 솔루션도 구해지지 않는다고 한다.
따라서 저자는 비선형 모형에서의 Embedded 방법으로 변수 선택을 할 수 있는 방법을 제안한다. 즉, 인공신경망을 통한 비선형 관계를 찾아내고 l0 정규화를 도입하여 변수 선택을 할 수 있게 한 것이다.
2. Problem Setup and Background
주어진 손실함수 L에 대하여 변수 부분 집합 S⊂{1,…,D} 그리고 파라미터 θ에 대한 평가는 다음과 같은 위험 함수를 통하여 이루어진다.
R(θ,s)=EX,YL(fθ(X⋅x),Y)
여기서 s∈{0,1}D이다. ⋅의 의미는 원소별 곱을 의미한다. Embedded 방법은 S와 θ를 동시에 찾되 ‖s‖0를 작게 하는 것이다. 여기서 ‖s‖0는 s의 0이 아닌 원소의 개수이다.
Feature Selection for Linear Models
먼저 선형 모형에서의 Embedded 방법을 생각해보자. 주어진 관측치 (xi,yi),i=1,…,n에 대하여 다음 제약이 포함된 목적함수를 최소화하는 방법이다.
1nn∑i=1(θtxi−yi)2s.t.‖θ‖0≤k
하지만 위 문제는 풀기가 까다로워서 l_0 대신 l_1 정규화를 생각하게 되는데 이것이 바로 LASSO이다.
하지만 이 방법은 선형 모형에 한정되어 있고 축소를 통하여 변수를 선택한다는 단점이 있다.
따라서 비선형 모형을 학습하면서 축소를 피하면서 변수를 선택하는 방법을 개발하는 것이 논문 저자의 목표가 된다.
3. Proposed Method
l0 페널티가 들어있으면 경사 하강법과 같은 방법으로 최적화할 수 없다. 따라서 이러한 제약을 극복하기 위해 확률적인 대체방법을 적용한다. 여기서는 Bernoulli Gate라는 개념을 소개한다.
집합 ˜S를 Bernoulli Gate라 하며 각 원소 ˜Sd는 다음을 만족한다.
P(˜Sd=1)=πd,d∈[D]={1,…,D}
논문의 저자는 모델의 파라미터 θ와 π를 추정하면 자연스럽게 변수 선택이 된다고 말하고 있다. l0 항이 이산형이므로 이를 직접적으로 최적화하는 것이 매우 어렵다. 이러한 점을 극복하기 위해 l0를 연속형으로 근사하는 방법인 Concrete, 또는 Hard-Concrete(HC)을 적용하기도 한다. 하지만 HC는 여전히 높은 분산을 갖는다는 문제점을 안고 있어 변수 선택에는 적절치 않다고 한다. 따라서 본 논문의 저자는 경험적으로 우수한 연속 분포를 개발한다고 한다.
Bernoulli Coninuous Relaxation for Feature Selection
변수 선택은 선택된 변수 집합에 대해서 안정성을 요구한다. Concrete나 HC는 Bernoulli Variable을 로지스틱 분포로 근사하는데 로지스틱 분포의 꼬리가 두꺼운 성질로 인하여 굉장히 높은 분산을 갖는다고 하며 이는 잘못된 변수 선택을 할 수 있다는 것이다. 이러한 단점을 극복하기 위해 Bernoulli Variable을 정규분포 기반으로 완화한 방법을 제안한다. 이를 Stochastic Gate(STG)라고 부르기로 하며 다음과 같이 정의한다.
zd=max(0,min(1,μd+ϵd))
여기서 ϵd는 N(0,σ2)에서 추출된 샘플이며 σ는 학습 과정에서 한 번만 추정된다. 이를 이용하면 Stochastic Gradient Decent(SGD) 방법으로 변수를 선택하면서 모형을 추정할 수 있다고 한다.
4. Connection to Mutual Information
여기서는 l0 기반 최적화 문제와 베르누이 분포의 모수 위에서의 최적화 문제가 동등한 것을 보이기 위하여 Mutual Information(MI) 을 사용한다.
4.1 Mutual Information based Objective
MI 관점에서 변수 선택의 목표는 결국 반응 변수 Y와 가장 MI가 큰 변수 집합 S를 고르는 것이다. 두 확률 변수 X,Y의 MI I(X;Y)는 다음과 같이 정의한다.
I(X;Y)=H(Y)−H(Y|X)
여기서 H(Y),H(Y|X)는 각각 엔트로피와 조건부 엔트로피이다.
이제 변수 선택 문제를 다음과 같은 최적화 문제로 만들어 볼 수 있다.
maxSI(XS;Y)s.t.|S|=k
k는 사전의 정의된 변수 개수이다.
4.2 Introducting Randomness
적절한 조건 하에서 S(또는 S의 Indicator Vector s)를 찾는 문제를 s를 모형화하는 분포의 모수를 추정하는 문제로 바꿀 수 있다.
가정 1) 다음을 만족하는 크기가 k인 인덱스 집합 S∗이 존재한다.
I(Xi;Y|X−{i})>0∀i
가정 2) I(XS∗c;Y|XS∗)=0
가정 1)은 S∗에 있는 변수를 모형에 포함시키면 예측력이 증가한다는 것이다. 가정 2)는 S∗이외에 다른 변수들은 관련성이 없다는 걸 의미한다. 위 가정들은 꽤나 순한 가정이라고 한다. 이러한 가정을 바탕으로 다음 성질이 만족된다고 한다.
성질 1)
(6)을 푸는 것과 다음을 푸는 것이 동치이다.
max0≤π≤1I(X⋅˜S;Y)s.t.∑iE[˜Si]≤k
여기서 ˜Si는 모수가 πi인 베르누이 분포를 따르는 확률 변수이다.
5. Related Work
여기서는 먼저 HC를 소개하는데 HC를 이용하면 빠른 수렴 속도와 일반화가 잘되는 것을 보장한다고 한다. 하지만 이걸 제안한 저자는 변수 선택의 안정성에 대한 평가를 하지 않았다고 한다.
여기서 제안하는 STG에 비해 HC는 높은 분산을 갖는 그라디언트 추정치를 만들어내는데 신경망 관련해서는 이 Sparse한 모형을 추정하는 문제에서 이 부분이 크게 문제 되지 않는다고 한다. 하지만 HC 기반 변수 선택은 매번 크게 바뀐다고 한다.
결국 HC는 별로 안 좋다는 이야기를 하는 것이다.
6. Experiments
여기서는 논문 저자들이 제안한 방법을 실험한 내용을 소개한다.
6.1 Synthetic Data in the D>N Regime
여기서는 데이터 개수보다 변수의 개수가 많은 상황에서 적절한 변수를 잘 뽑아내는지 확인하는 실험 해보고 결과를 소개한다. 여기서는 MADELON 데이터를 사용했다고 한다.
또한 Friedman의 회귀 데이터를 이용하여 500개 중에서 실제로 관련성이 높은 변수는 5개이고 나머지는 쓸데없는 변수인 상황에서 논문에서 제안하고 있는 방법이 실제로 관련성이 높은 변수를 잘 선택하는지 확인하는 실험도 진행하였다.
실험 결과는 다음과 같다.
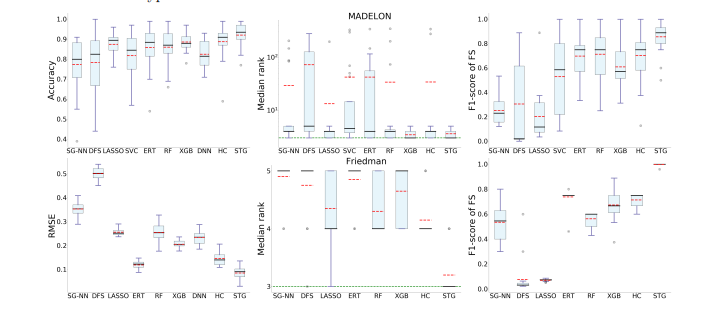
첫 번째 열은 MADELON 데이터, 두 번째 열은 Friedman 회귀 데이터이다. 두 번째 열을 난 좀 더 주목했는데 두 번째 열에서 가운데 그림을 보면 실제로 변수 관련성 있는 변수들의 순위의 중앙값이다. 이 값이 작을수록 해당 변수를 잘 뽑았다는 것이다. 실제로 그래프를 보면 관련성 있는 변수를 STG 방법이 더 잘 선택했다는 것을 알 수 있다. RMSE도 가장 낮았다(좌측 그림).
6.2 Noisy Binary XOR Classification
XOR 형태를 갖는 데이터에서 XOR을 발생시키는 변수를 선택할 수 있는지 확인하는 실험이었다. 역시 STG가 가장 좋았다고 한다.
6.3 Classification on Real World Data
실험용 데이터에 대해서만 실험하면 리젝되니까 실제 데이터에 대해서도 STG의 유효성을 검증해본 것이다.
7. Cox Proportional Hazard Models for Survival Analysis
Cox 모델에 STG를 적용하여 Cox-STG라는 것을 제안했다. 유방암 데이터를 가지고 생존 모형을 적용하여 관련성 높은 변수를 추출하고자 했다. 다른 모형에 비해 Cox-STG가 가장 적은 그리고 관련성 높은 변수를 추출하였다.
8. Evaluating Stochastic Regularization Schemes
여기서는 Non Convex 정규화와 노이즈 주입에 대한 이득과 Logistic HC에 비해 Gaussian 기반 STG가 갖는 이점에 대해서 논의하였다.
Non Convex 정규화와 노이즈 주입(Injected Noise)를 이용하면 기존 LASSO보다 실제 관련 변수를 찾아내는데 필요한 샘플 수가 더 적다고 한다. 또한 STG가 HC 보다 더 분산이 작아서 더 안정적인 과정이라는 것도 실험적으로 증명했다.
또한 STG는 전진 선택법과는 달리 한번 변수가 빠져나갔다 하더라도 게이트에 의하여 다시 들어올 수 있는 여지를 만들어 놓았다는 특징이 있다.
Logistic HC에 비해 Gaussian 기반 STG가 갖는 이점은 Gaussian 분포가 로지스틱 분포보다 꼬리가 얇아서 변수 선택에는 유리하다는 점이다. 아마도 꼬리가 얇기 때문에 매 시행마다 이상한 값이 튀어나올 가능성이 적어서 매번 일치성을 갖는 변수 선택이 가능하다는 뜻인 것 같다.
9. Feature Selection with Correlations
여기서는 변수들끼리 상관관계가 있을 때(다중공선성이 있을 때) 변수 선택에 어려움이 생긴다. 제안된 방법이 잘 작동하는지 확인해보고자 한다.
여기서는 두 가지 상황을 고려했다. 첫 번째는 변수를 똑같이 복사했을 때(상관관계가 완벽한 경우) 복사된 변수를 선택하는지 알아보았고 두 번째는 많은 변수들이 실제로 소량의 변수들의 함수일 때 그 많은 변수 중에서 실제로 소량의 변수를 잘 식별해내는지 알아보는 것이었다.
실제로 STG가 이러한 상황에서도 잘 식별해내는 것을 실험적으로 증명하였다.
10. Conclusion
이 논문에서는 STG를 사용한 Embedded 변수 선택 방법을 제안하였다. 제안된 방법은 기존 인공 신경망과 같은 비선형 모형에서 l1 정규화 문제보다 더 많은 이점을 갖고 있었다. 심지어 모형 성능을 해치지 않고서 말이다.
'통계 > 논문 리뷰' 카테고리의 다른 글
| Multivariate Adaptive Regression Splines (2) | 2022.09.13 |
|---|---|
| “Why Should I Trust You?” Explaining the Predictions of Any Classifier (2) | 2022.08.17 |
| A Unified Approach to Interpreting Model Predictions (0) | 2022.08.15 |
| Producer Incentives in Cost Allocation (0) | 2022.08.11 |
| Monotonic Solutions of Cooperative Games (0) | 2022.08.11 |





댓글