단위근 검정으로 (Augmented) Dickey-Fuller Test와 더불어 유명한 Phillips-Perron Test 검정이 있다. 이 검정 방법이 궁금해서 해당 논문을 읽어보고 그 내용을 정리했다.
이번 포스팅에서는 Phillips-Perron Test 검정의 바탕이 되는 논문 "Testing for A Unit Root in Time Series Regression"을 리뷰하고자 한다.
본 포스팅에서는 수식을 포함하고 있습니다.
티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니
PC 웹 브라우저 또는 모바일 웹 브라우저에서 보시기 바랍니다.
목차는 다음과 같다.
4. Limiting Distributions of the Statistics
5. Statistical Inference in the Presence of a Unit Root
6. Power Functions for Unit Root Tests
0. Summary
본 논문은 일반적인 시계열 모형에서 단위근 존재 여부를 탐지하는 새로운 검정법을 제안한다. 본 논문의 접근 방법은 nuisance 모수에 대한 비모수적 방법이며 그에 따라 약하게 종속되거나 혹은 (시간에 따른) 등분산성을 만족하지 않는 시계열 데이터에 대해서도 적용 가능하다.
여기서 제안하는 검정법은 절편항이 있거나 또는 절편항과 선형 추세가 포함된 시계열 모형에서 단위근 존재 여부를 판별한다. 여기서 판별하는 가설은
H0:Exists a Unit Root vs H1:Time Series is Stationary
이다.
여기서는 귀무가설이 참일 때와 대립 가설하에서 검정 통계량의 극한 분포를 유도한다. 마지막에 비중심 분포 이론은 검정 통계량에 대한 로컬한 점근 검정 함수를 유도할 수 있게 하며 이는 기존 Dickey-Fuller Test와 비교할 수 있게 한다. 소표본에서의 검정능력에 대한 시뮬레이션 결과 또한 이 논문에서 소개한다.
1. Introduction
Parametric 시계열 모형에서 단위근을 탐지하는 방법이 최근(1980년대) 인기를 통계학과 그 응용 분야에서 매력적이라고 한다. Fuller와 Dickey의 최근 논문은 이러한 방법들을 리뷰한 것이다. 가장 마지막 논문은 공식적인 검정법 사용에 대한 실용적인 가이드라인을 제안한다. 잘은 모르겠지만 내 생각엔 어떤 단위근 검정법을 어떤 경우에 써야 하는지에 대한 가이드라인을 제공한 것 같다.
단위근 검정의 주된 적용 분야는 경제학이라고 한다. 경제 분야에서 시계열에 단위근이 존재하는 사례들이 많기 때문이라고 한다. 단위근 검정법은 추세(Trend)가 단위근 존재 현상으로 인한 확률적(Stochastic) 추세인지 아니면 결정적(Deterministic) 다항 추세인지를 결정하는 데 사용되기도 한단다.
최근 Said와 Dickey는 Dickey-Fuller의 회귀 t-test가 시계열 모형이 ARIMA(p,1,q)인 경우(p,q unknown)에서도 lag-length가 샘플 사이즈 T가 증가함에 따라서 T1/3 속도로 증가한다면 여전히 사용될 수 있을 거라고 했다.
Dickey-Fuller Test의 대안으로 Phillips이 제안한 단위근 검정 방법은 nuisance 모수에 대한 비모수적인 방법이며 이에 따라 매우 넓은 종류의 (단위근이 존재하는) 시계열 모형에 적용할 수 있다고 한다. 동일한 분포를 갖는(Identically Distributed)를 갖는 오차항뿐 아니라 시간에 따른 등분산성을 만족하지 않는 시계열 모형이 그 예가 되겠다.
특히 실제 시계열 모형에서 이동 평균 요소가 들어간다면 Phillips의 검정법이 Dickey-Fuller, Said-Dickey가 제안한 검정법보다 훨씬 좋은 대안이 될 것이라고 한다.
Phillips가 제안한 단위근 검정법은 시계열 모형에 절편항이 있거나 선형 추세가 있는 경우로 확장할 수 있다. 이러한 확장은 유의한 절편항을 갖는 시계열이 자주 관측이 되는 분야라면 매우 중요하다. 또한 경제학 분야에서는 결정적 선형 추세를 갖는 시계열에서 단위근의 존재를 판별하는 것 또한 중요하다.
여기서 제안하는 방법은 점근적이며 함수의 약수렴성에 의존한다고 한다. 따라서 당연히 소표본에서의 성능이 얼마나 차이가나는지 확인하는 것은 중요할 것이다. Phillips 검정 통계량의 극한 분포는 표준 Brownian Motion의 Functional로 표현되며 Fuller가 이를 테이블로 정리해놨다고 한다. 점근 국소 검정 성질(? The Asymptotic Local Properties)가 near-integrated Process에 대해서 연구 되었다. 소표본에서의 검정능력에 대한 시뮬레이션 결과 또한 이 논문에서 소개하며 증명 과정은 부록에 남겨둔다.
2. Preliminaries
여기서 다루는 모델은 오차의 시간에 따른 시퀀스 (sequence) ut로부터 얻어진다. 이때 이 논문에서 ut에 대한 다음과 같은 조건을 가정한다.
(A) E(ut)=0 for all t(B) suptE|ut|β+ϵ<∞ for some β>2 and ϵ>0(C) σ2=limT→∞E(T−1S2T) exists and σ2>0 where St=t∑j=1uj(D) {ut}is strong mixing with coefficients αmthat satisfy
∞∑m=1α1−2/βm<∞
이러한 조건은 오차들이 약한 종속성을 갖고 있거나(D) 시간에 따른 오차의 등분산성이 만족되지 않더라도 시계열에서의 단위근 검정을 적용할 수 있게 해 준다. 조건 (B)를 보면 오차의 2차보다 큰 모멘트가 유한하다는 조건인데 이는 모든 시간 t에 대해서 2차 모멘트가 같다는 조건, 즉 오차의 등분산성을 완화시킨 것이다.
논문에서 제안하는 단위근 검정은 유한 차수의 ARMA처럼 다양한 시계열 모형에 적용할 수 있다.
다음으로 이 논문에서 제공하는 이론적 정리에 필요한 St,ut의 성질들을 나열하고 있다(요건 생략).
그리고 특별한 언급이 없으면 Summation ∑은 t=1,…,T까지의 합이다.
3. The Models and Estimators
yt를 아래 모형에서 생성된 시계열이라고 하자.
yt=αyt−1+ut, t=1,2,…
α=1
이때 초기 시간 t=0이고 y0는 임의의 랜덤 변수이며(고정 상수가 될 수 있다) 그 분포는 고정되어있고(아마도 t에 따라서 변하지 않다는 뜻 같다) 샘플 사이즈 T와는 독립이다. 그리고 Innovation(또는 오차항) ut은 조건 (A)-(D)를 만족한다.
여기서는 다음의 회귀 방정식을 고려한다.
yt=ˆμ+ˆαyt−1+ˆut
yt=˜μ+˜β(t−T/2)+˜αyt−1+˜ut
여기서 (ˆμ,ˆα),(˜μ,˜β,˜α)는 최소제곱추정량이다.
식 (5)의 경우 디자인 매트릭스 X는 T×3 행렬을 이용한다. 그리고 다음의 t 통계량을 정의한다.
tˆα=(ˆα−α)(∑(yt−1−ˉy−1)2)1/2/ˆstˆμ=(ˆμ−μ)(∑(yt−1−ˉy−1)2/∑y2t−1)1/2/ˆst˜μ=(˜μ−μ)/(˜s2c1)1/2t˜β=(˜β−β)/(˜s2c2)1/2t˜α=(˜α−α)/(˜s2c3)1/2
여기서 ˆs,˜s는 표준 오차라고 한다(정확한 의미는 안 나와있다 오차의 표준편차 추정치라고 일단 생각했다). 그리고 cj는 (X′X)−1 j번째 대각 원소다. (근데 ˉy−1은 뭐지? 그냥 표본 평균인가?? 나와있지 않았다)
Dickey와 Fuller가 그랬던 것처럼 여기에서도 식 (4), (5)에서의 회귀 계수 추정량 그리고 t 통계량이 실제 모형이 (2), (3)인 경우의 극한 분포에 관심을 구해야 할 것이다. 그래야 P Value를 구할 수 있을 테니까.
이때 귀무가설은 H0:α=1,μ=β=0이다. 이때 식 (2)은 다음과 같이 바꿔도 된다고 한다.
yt=μ+αyt−1+ut,t=1,2,…
왜냐하면 ˜α나 이에 해당하는 t 통계량이 μ에 대해서 불변하기 때문이다. 이에 따라 ˆα와 이에 대응하는 t 통계량의 확률분포와 점근 분포도 변하지 않는다.
그리고 yt와 ut의 모멘트 성질을 정리했다.
4. Limiting Distributions of the Statistics
여기에서는 각 회귀 추정량과 그에 대응하는 t 통계량의 극한 분포에 대한 정리(Theorem 1)를 다룬다. 이 정리를 통해 만약 ut가 IID라면 σ2=σ2U이 되어 각 추정량과 통계량의 극한 분포가 nuisance parameter σ2에 의존하지 않게 된다.
그리고 각 극한 분포에 대한 p value와 기각값은 Dickey-Fuller 논문 테이블에 있다고 한다.
정리 1은 기존 Dickey-Fuller 결과에서 약한 종속 관계를 갖거나 등분산성이 아닌 오차항을 포함하는 시계열에 대해서도 확장할 수 있다. 그리고 이러한 결과를 이용하면 좀 더 넓은 종류의 Innovation ut에 대해서 일반적인 극한 분포를 보여준다고 한다. 즉, Phillips와 Perron의 결과가 더 일반적이라는 것이다.
여기서 ut의 IID 조건이 σ2=σ2U의 필요조건은 아니라고 한다.
여기서 σ2U=limT→∞∑E(u2t)이다. 즉, ut가 IID가 아니라 하더라도 σ2=σ2U일 수 있는 것이다. 그런 경우중 하나가 바로 오차항 ut가 마틴게일(Matingale) 차이로 표현되는 경우이다. 따라서 오차항이 마틴게일 차이로 표현되면 등분산성을 만족하지 못하더라도 σ2=σ2U이 되어 Dickey-Fuller 검정은 유효하게 된다. 하지만 σ2≠σ2U인 경우 Dickey-Fuller 검정은 정확한 점근 사이즈(점근 유의 수준)를 얻을 수 없다고 한다.
5. Statistical Inference in the Presence of a Unit Root
σ2≠σ2U인 경우 앞에서 구한 극한 분포가 nuisance 모수에 의존하게 되기 때문에 문제가 복잡해진다. 하지만 σ2,σ2U이 Consist 하게 추정할 수 있기 때문에 nuisance 모수를 점근적으로 제거할 수 있는 변환(Transformation)이 존재한다고 한다. 이러한 아이디어는 Phillips가 처음으로 개발했고 이러한 변환 과정은 절편항 또는 선형 추세를 포함하는 회귀 모형에서의 단위근 검정으로 확장될 수 있다고 한다.
σ2U의 일치 추정량은 여러 가지가 있지만 종종 식 (5)와 같은 회귀 모형을 다루고 싶은 경우가 많아 일치 추정량은 ˜s2으로 선정한다(ˆs2도 σ2U의 일치 추정량이다). σ2에 대한 일치추정량은 Phillips가 논의했다고 하는데 많은 추정량이 있다고 한다. 그중에서 Truncated Autocovariance를 기반으로 한 추정량을 소개하고 일치성 조건을 이야기한다. 이는 오차항이 serially 상관성을 갖는 경우에도 적용시키기 위한 것이었다.
이러한 조건을 소개하고 본 논문에서 위 추정량을 σ2의 일치 추정량으로 선택했다. 하지만 이 추정량은 분산 추정량이므로 양수가 되어야 하는 게 일반적이지만 상황에 따라 음수가 나오는데 이를 해결하기 위한 방법을 소개하며 최종적인 σ2의 일치 추정량은 다음과 같다.
ˆσ2Tl=T−1∑ˆu2t+2T−1l∑s=1wslT∑t=s+1ˆutˆut−s
˜σ2Tl=T−1∑˜u2t+2T−1l∑s=1wslT∑t=s+1˜ut˜ut−s
여기서 wsl=1−s/(l+1)이다.
식 (7), (8)에서 serially 상관성과 관련된 추정값이 포함되어 있다는 걸 주목해야한다. 이는 앞에서 말했듯이 오차항이 serially 상관성을 갖는 경우도 포함시키기 위한 것이다.
다음으로 이러한 일치 추정량을 바탕으로 변환 Z를 정의한다(이를 Z 통계량이라 하자). 이러한 Z 통계량은 1987년 Phillips가 개발한 방법을 절편항이 없거나 선형 추세가 없는 회귀 모형으로 확장한다고 한다.
Z 통계량에 아이디어는 기존 회귀 통계량을 serially 상관이 있는 오차나 등분산성을 만족하지 않는 오차를 가진 시계열에도 적용시키기 위한 것이었다고 한다.
그리고 이러한 Z 통계량의 분포가 점근적으로 nuisance 모수에 의존하지 않는다는 것을 정리를 소개한다(Theorem 2).
Theorem 2는 σ2=σ2U인 경우 Z 통계량의 극한 분포가 약한 종속성을 갖거나 등분산성을 만족하지 않는 오차항을 갖는다 해도 불변한다는 것을 보여주며 이는 Z 변환을 적용시키기 전의 극한 분포와 같다(Section 4).
6. Power Functions for Unit Root Tests
이번 섹션에서는 단위근 검정의 점근 검정력 함수를 발전시키는데 다음과 같은 형태를 고려한다.
α=ec/T
c=0인 경우는 귀무가설이 되며, c>0인 경우는 Loacal explosive alternative가 되고 c<0인 경우는 로컬 정상성(Local Stationary)이 된다.
식 (2) 또는 (2')에서 α가 (10)과 같은 형태를 Phillips는 Near-Integrated라고 명명했다.
다음으로 Theorem 3을 소개하는데 이 정리 시계열 yt가 Near-Integrated인 경우 자기회귀계수 추정량 α와 그에 대한 t 통계량에 대한 내용을 골자로 한다.
그리고 이러한 결과를 통해 더 일반적인 오차항을 고려하더라도 Dickey-Fuller 검정 과정에 비하여 점근적 검정력의 손실이 없다고 한다.
7. Experimental Evidence
여기서는 이 논문에서 제안하는 검정법에 대한 모의실험을 진행하고 Said, Dickey의 결과를 비교하여 이 새로운 검정법이 적절한지 확인한다.
기존 Said와 Dickey 논문에서 증명한 극한 분포는 Z 변환을 이용하면 이 논문에서 얻은 결과와 동일하다고 한다. 하지만 회귀 계수 추정량에 기반한 극한 분포는 Said와 Dickey는 nuisance parameter 때문에 제안하지 못했다고 한다. 따라서 본 논문의 저자는 자기들의 방법이 더 우수하다고 한다.
시뮬레이션에서 사용한 모형은 (2)이며 오차항 ut는 다음과 같은 구조로 생성되었다고 한다.
ut=et+θet−1
이때 θ값을 조정하면서 시뮬레이션 결과(귀무가설이 참일 때 극한 분포의 기각값과 α=0.85 대립가설에 대한 검정력)를 정리했다.
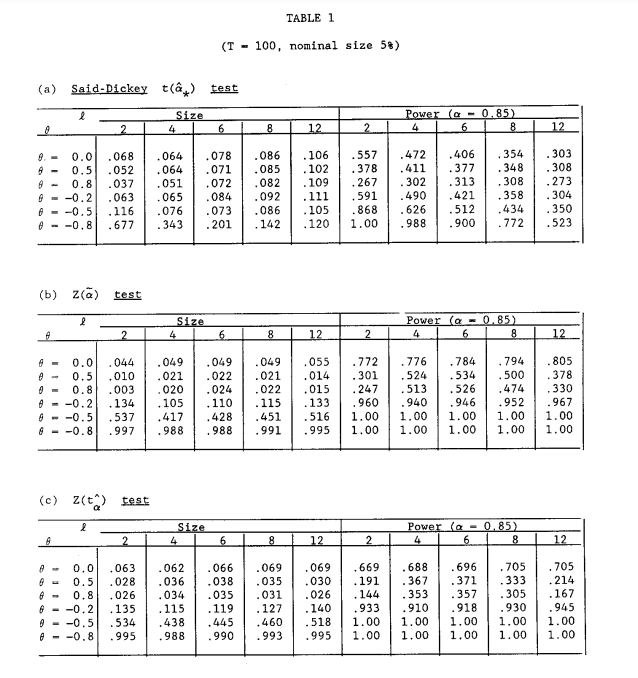
시뮬레이션 결과 본 논문에서의 검정이 Said와 Dickey 보다 좀 더 보수적이고 검정력은 더 높았다고 한다.
여기서 두 Z 통계량 Z(ˆα)과 Z(tˆα)을 쓴 이유가 엿보였다(물론 내생각이다. 하지만 논문 어디에서 왜 두개를 고려했는지에 대한 설명이 없었다). Said-Dickey가 제안한 검정 통계량 보다 더 우월하다는 것을 유리하게 비교하기 위하여 Z통계량 2개를 제안한 것이 아닌가 싶다. 실제로 시뮬레이션 결과를 이야기할 때 그랬다.
또한 자기 회귀 차수가 높아짐에 따라 Said-Dickey 검정법의 검정력은 꽤나 급격하게 떨어졌는데 본 논문에서의 검정력은 그렇지 않았다. 즉, 자기 회귀 차수가 높아짐에 따라 이 논문에서 제안한 검정법이 안정적이다는 것을 보여준다.
하지만 θ<0인 경우 기각값(critical)이 높게 나와서 대부분 귀무가설을 기각하는 결과가 나와서 본 논문의 검정법 유용성이 떨어지기도 했다. 하지만 이 상황에서 Said Dickey도 안 좋았다고 한다.
그리고 점근 이론 등을 통하여 이러한 결과가 나오는 이유에 대해서 설명한다.
8. Concluding Comments
이 논문에서 제안한 방법은 정상 과정(Stationary Process)이거나 추세 정상 과정(Trend Stationary Process)인 단일 시계열에서의 단위근이 존재하는지에 대한 심플한 검정방법을 제공한다. 왜냐하면 오직 1차 자기 회귀 계수의 추정치와 Z 변환만 하면 되기 때문이다.
하지만 이것도 점근성에 많이 의존하다 보니 소표본에서의 결과가 점근 이론 결과와 매우 달라질 수 있다는 것 또한 보여주었고 실험 결과에 대해서 한 번 더 정리하며 이 논문은 끝이 난다.






댓글