반갑습니다~ 꽁냥이입니다. 이진 트리(Binary Tree)는 컴퓨터 자료구조에서 이진 탐색 트리(Binary Search Tree), 의사결정나무(Decision Tree)를 시각화할 때 많이 사용되는 데이터 구조입니다. 특히 이러한 이진 트리 구조는 그 자체로도 중요하지만 이를 시각화하는 것이 꽤나 어려워서 논문의 주제가 될 정도인데요. 이번 포스팅에서는 Matplotlib을 이용하여 이진 트리를 시각화해보는 방법을 알아보겠습니다. 사실 제가 소개하는 방법은 완벽하지 않고 효율적이지도 않지만 그래도 나름 잘 그려지는 것 같아서 공유해보려고 해요 ㅎㅎ.
여기서는 이진 트리와 Traverse In Order에 대한 기본적인 개념은 알고 있다고 가정합니다. 또한 부모 노드가 반드시 왼쪽, 오른쪽 자식 노드를 두 개 갖는 이진 트리를 다룹니다.
여기서 다루는 내용은 다음과 같아요.
2. Matplotlib을 이용하여 이진 트리 시각화 하기
1. 이진 트리 시각화 원칙
이진 트리를 예쁘게 그리기 위해서 원칙을 갖고 그리게 됩니다. 여기서는 그 원칙에 대하여 몇 가지 소개하려고 합니다. 먼저 노드가 속한 층(Level)이라는 개념을 먼저 소개하겠습니다. 여기서 노드가 속한 층이라는 것은 그 노드의 부모 노드의 개수 + 1로 정의하겠습니다. 예를 들어 아래 그림에서 2, 3번 노드, 4, 5번 노드는 같은 층에 속해있습니다.

위 그림은 이진 트리를 시각화로 나타낸 것인데요. 뭔가 삐뚤삐뚤해 보여서 예뻐 보이지 않네요.. 이때 이진 트리 시각화 원칙 1은 다음과 같습니다.
이진 트리 시각화 원칙 1
같은 층에 있는 노드들은 한 직선 위에 있어야 하며 층을 연결하는 직선들은 서로 평행해야 한다.
아래 그림은 원칙 1을 적용한 것(왼쪽)과 그렇지 않은 이진 트리(오른쪽)를 나타낸 것입니다.
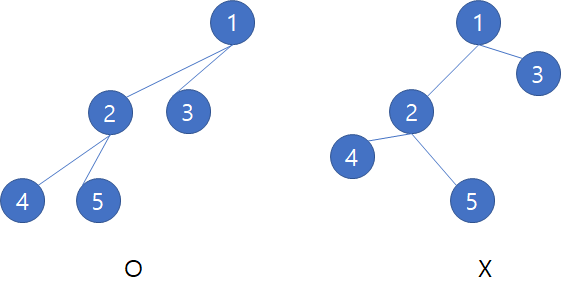
원칙 1을 적용한 것이 좀 더 정돈된 느낌이 나지만 아직은 부족해보입니다. 즉, 원칙 1만 가지고는 이진 트리를 예쁘게 그리기에는 한계가 있어요. 이번엔 원칙 2를 소개하겠습니다.
이진 트리 시각화 원칙 2
한 노드의 왼쪽 자식 노드는 부모 노드 왼쪽에 오른쪽 자식 노드는 부모 노드 오른쪽에 있어야 한다.
아래 그림은 원칙 1, 2를 적용한 것(왼쪽)과 원칙 1만 적용된 이진 트리(오른쪽)입니다.
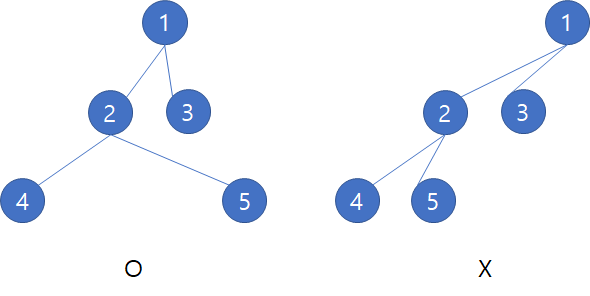
원칙은 지켜졌지만 아직 뭔가 더 부족해 보입니다. 이제 마지막 원칙을 소개하겠습니다.
이진 트리 시각화 원칙 3
부모 노드는 자식 노드 위에 중간에 있어야 한다.
아래 그림은 원칙 1, 2, 3을 적용한 것(왼쪽)과 원칙 1, 2만 적용된 이진 트리(오른쪽)입니다.

확실히 원칙 1, 2, 3을 모두 적용한 것이 직관적이고 깔끔해 보입니다. 이제 꽁냥이는 이러한 원칙을 만족시키는 이진트리를 Matplotlib을 이용하여 그려보려고 해요.
2. Matplotlib을 이용하여 이진 트리 시각화 하기
이제 앞서 소개한 원칙을 바탕으로 Matplotlib을 이용하여 이진 트리를 시각화해보겠습니다.
2.1 모듈 및 클래스 정의
먼저 필요한 모듈을 임포트합니다.
import matplotlib.pyplot as plt
import seaborn as sns
그리고 이진 트리의 기본 단위인 노드(Node) 클래스를 정의합니다. 노드 클래스에는 x, y 좌표와 텍스트(text) 정보를 담기 위한 필드와 루트 노트(isRoot)인지, 부모 노드(parentNode), 자식 노드(leftChild, rightChild)는 무엇인지 확인하기 위한 필드를 정의했습니다. 추가적으로 끝 마디 여부(isLeaf)에 대한 정보를 담는 필드도 정의하였습니다. 메서드 같은 경우 노드의 층 정보를 가져오는 getLevel, 왼쪽, 오른쪽 자식 노드를 설정하는 메서드도 정의하였습니다.
class Node:
def __init__(self):
self.x = None
self.y = None
self.text = ''
self.isRoot = False
self.parentNode = None
self.leftChild = None
self.rightChild = None
self.isLeaf = False
def getLevel(self, cnt = 1):
if self.isRoot:
return cnt
else:
cnt += 1
cnt = self.parentNode.getLevel(cnt)
return cnt
def setLeftChild(self, node):
self.leftChild = node
node.parentNode = self
def setRightChild(self, node):
self.rightChild = node
node.parentNode = self
다음으로 Tree 클래스를 정의하였습니다. 이 클래스는 뿌리 노드를 초기 값으로 받습니다. 메서드의 경우 뿌리 노드를 가져오는 getRoot, 브랜치의 길이는 계산하는 getLengthOfBranch, 트리의 깊이를 계산하는 getDepth, Traverse In Order로 노드 리스트를 만드는 traverseInOrder, 트리에서 가장 오른쪽에 있는 노드를 가져오는 getRightMostNode, 가장 왼쪽에 있는 노드를 가져오는 getLeftMostNode, 서브 트리의 거리를 계산하는 getDistanceBetweenSubtrees, 나무를 x축으로 이동시키는 moveTree를 정의하였습니다.
class Tree:
def __init__(self, root):
assert root.isRoot, 'node should be specified as root'
self.__root = root
def getRoot(self):
return self.__root
def getLengthOfBranch(self, node, cnt = 1):
if node.parentNode is None:
return cnt
else:
cnt += 1
return self.getLengthOfBranch(node.parentNode, cnt)
def getDepth(self, remove_Leaf=False):
all_nodes = self.traverseInOrder()
if remove_Leaf:
depth = max([self.getLengthOfBranch(node) for node in all_nodes if not node.isLeaf])
else:
depth = max([self.getLengthOfBranch(node) for node in all_nodes])
return depth
def traverseInOrder(self, node=None):
if node is None:
node = self.__root
res = []
if node.leftChild != None:
res = res + self.traverseInOrder(node.leftChild)
res.append(node)
if node.rightChild != None:
res = res + self.traverseInOrder(node.rightChild)
return res
def getRightMostNode(self, node = None, level = None):
if node is None:
node = self.__root
if level is None:
return [nd for nd in self.traverseInOrder(node)][-1]
else:
return [nd for nd in self.traverseInOrder(node) if nd.getLevel()==level][-1]
def getLeftMostNode(self, node = None, level = None):
if node is None:
node = self.__root
if level is None:
return [nd for nd in self.traverseInOrder(node)][0]
else:
return [nd for nd in self.traverseInOrder(node) if nd.getLevel()==level][0]
def getDistanceBetweenSubtrees(self):
root.leftChild.parentNode = None
root.rightChild.parentNode = None
root.leftChild.isRoot = True
root.rightChild.isRoot = True
left_subtree = Tree(root.leftChild)
right_subtree = Tree(root.rightChild)
if left_subtree.getDepth() == right_subtree.getDepth():
level = right_subtree.getDepth()
elif left_subtree.getDepth() > right_subtree.getDepth():
level = right_subtree.getDepth()
else:
level = left_subtree.getDepth()
lrmn = left_subtree.getRightMostNode(level=level)
rlmn = right_subtree.getLeftMostNode(level=level)
x_diff = rlmn.x - lrmn.x
root.leftChild.parentNode = root
root.rightChild.parentNode = root
root.leftChild.isRoot = False
root.rightChild.isRoot = False
return x_diff
def moveTree(self, shift=1):
for nd in self.traverseInOrder():
nd.x = nd.x+shift
return2.2 아이디어
이제 이진 트리를 그리기 위한 꽁냥이의 아이디어(사실 여러 자료 참고했어요)를 소개하겠습니다.
1 단계
먼저 주어진 트리에 초기 x, y 좌표를 부여합니다. x좌표는 Traverse In Order를 이용하여 이 순서대로 0부터 시작하여 1씩 증가시켜 부여하고 y좌표는 해당 노드의 층 정보를 이용하여 0부터 시작하여 1씩 증가시켜 부여합니다.

2 단계
한 노드를 뿌리 노드로 하는 왼쪽 서브 트리와 오른쪽 서브트리에 대하여 최소 거리를 설정하고 최소 거리만큼 유지 되도록 왼쪽 서브트리와 오른쪽 서브 트리를 이동시킵니다. 이때 최소 거리는 깊이가 얕은 서브 트리의 가장 아래보다 더 아래층은 고려하지 않습니다. 그리고 왼쪽 서브 트리에서 가장 오른쪽에 있는 노드와 오른쪽 서브 트리에서 가장 왼쪽에 있는 노드의 x 좌표를 기준으로 계산합니다.
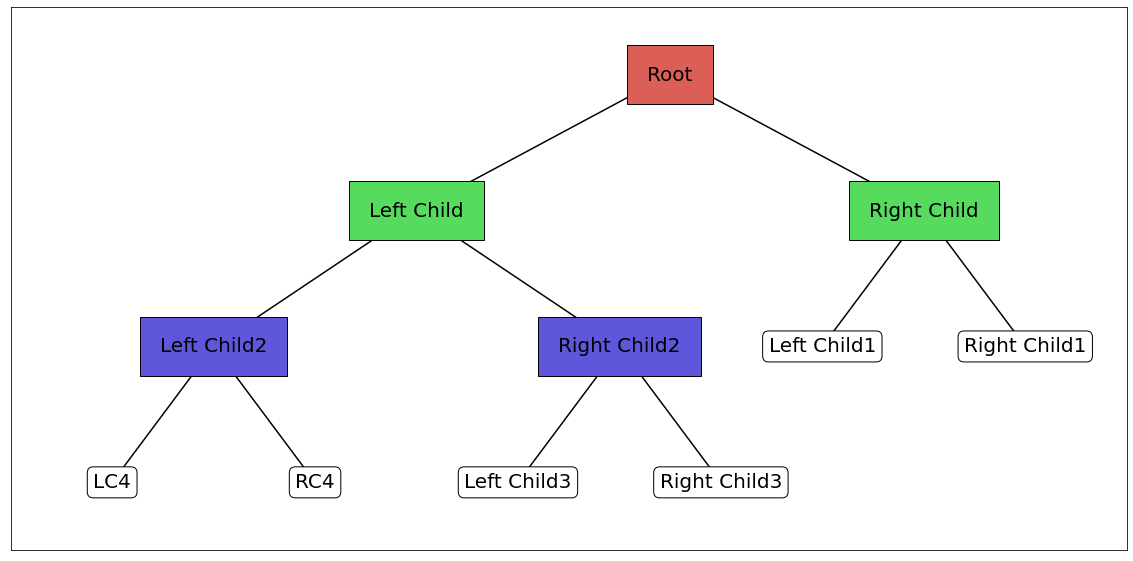
아래 그림을 통하여 설명하면 1번을 기준으로 오른쪽 서브 트리(초록 박스)가 깊이가 얕으므로 오른쪽 서브 트리의 가장 아래층보다 더 아래에 있는 4, 5번은 최소 거리를 계산할 때 고려하지 않습니다. 따라서 왼쪽 서브 트리(빨간 박스)에서 가장 오른쪽에 있는 노드는 5번이 아니라 2번이 되고요. 오른쪽 서브 트리에서 가장 왼쪽에 있는 노드는 3번 노드가 됩니다. 따라서 2, 3번 노드가 최소 거리가 되도록 각 서브 트리를 옮겨주게 됩니다.

3 단계
뿌리 노드가 자식 노드의 중앙에 오도록 뿌리 노드의 위치를 이동시킵니다.

4 단계
2~3단계 과정을 서브 트리 간 거리가 정해둔 최소 거리가 될 때까지 반복합니다. 이때 무한 루프에 빠지지 않도록 최대 반복수는 나무의 깊이만큼 설정해줍니다.
2.3 구현
이제 아이디어를 소개했으니 구현을 해보겠습니다. 먼저 나무를 만들어보겠습니다.
root = Node()
root.isRoot = True
root.text = 'Root'
left_child = Node()
left_child.text = 'Left Child'
root.setLeftChild(left_child)
right_child = Node()
right_child.text = 'Right Child'
root.setRightChild(right_child)
l_child = Node()
l_child.text = 'Left Child1'
l_child.isLeaf = True
right_child.setLeftChild(l_child)
r_child = Node()
r_child.text = 'Right Child1'
r_child.isLeaf = True
right_child.setRightChild(r_child)
ll_child = Node()
ll_child.text = 'Left Child2'
left_child.setLeftChild(ll_child)
rr_child = Node()
rr_child.text = 'Right Child2'
left_child.setRightChild(rr_child)
lll_child = Node()
lll_child.text = 'Left Child3'
lll_child.isLeaf = True
rr_child.setLeftChild(lll_child)
rrr_child = Node()
rrr_child.text = 'Right Child3'
rrr_child.isLeaf = True
rr_child.setRightChild(rrr_child)
llll_child = Node()
llll_child.text = 'LC4'
llll_child.isLeaf = True
ll_child.setLeftChild(llll_child)
rrrr_child = Node()
rrrr_child.text = 'RC4'
rrrr_child.isLeaf = True
ll_child.setRightChild(rrrr_child)
tree = Tree(root)
먼저 이 나무를 노드의 층과 Traverse In Order를 이용하여 x, y 좌표를 부여해보았습니다. 아래 코드는 부여한 x, y좌표를 이용하여 scattor plot을 그려본 것입니다. 이때 draw_connect_line 함수는 노드와 노드를 연결하는 선을 그려주는 함수입니다.
def draw_connect_line(node):
if node is not None:
if node.parentNode is not None:
plt.plot((node.parentNode.x, node.x), (node.parentNode.y, node.y),color='k')
draw_connect_line(node.leftChild)
draw_connect_line(node.rightChild)
for i, nd in enumerate(tree.traverseInOrder()):
nd.x = i
nd.y = -(nd.getLevel()-1)
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
x_coords = []
y_coords = []
for nd in tree.traverseInOrder():
x_coords.append(nd.x)
y_coords.append(nd.y)
draw_connect_line(root)
plt.scatter(x_coords, y_coords)
plt.show()

위 그림에서 다른 쪽은 문제없으나 맨 위쪽 뿌리 노드가 자식 노드에 대하여 중앙에 있지 않다는 것을 알 수 있습니다. 이제 이를 수정하도록 하겠습니다. 아래 코드는 꽁냥이의 꿈을 실현시켜줄 함수입니다 ㅎㅎ. 이 함수는 이진 트리(tree)와 최소 거리(offset)을 인자로 받는 함수인데요. 코드를 자세히 살펴보겠습니다.
def drawing_binary_tree(tree, offset):
for i, nd in enumerate(tree.traverseInOrder()):
nd.x = i
nd.y = -(nd.getLevel()-1)
def tidy_drawing_tree(tree):
root = tree.getRoot()
if root.leftChild is None and root.rightChild is None:
return
else:
root.leftChild.parentNode = None
root.rightChild.parentNode = None
root.leftChild.isRoot = True
root.rightChild.isRoot = True
left_subtree = Tree(root.leftChild)
right_subtree = Tree(root.rightChild)
if left_subtree.getDepth() == right_subtree.getDepth():
level = right_subtree.getDepth()
elif left_subtree.getDepth() > right_subtree.getDepth():
level = right_subtree.getDepth()
else:
level = left_subtree.getDepth()
lrmn = left_subtree.getRightMostNode(level=level)
rlmn = right_subtree.getLeftMostNode(level=level)
x_diff = rlmn.x - lrmn.x
shift = offset - x_diff
right_subtree.moveTree(shift=shift/2)
left_subtree.moveTree(shift=-shift/2)
tidy_drawing_tree(left_subtree)
tidy_drawing_tree(right_subtree)
root.x = (root.leftChild.x + root.rightChild.x)/2
root.leftChild.parentNode = root
root.rightChild.parentNode = root
root.leftChild.isRoot = False
root.rightChild.isRoot = False
max_cnt = tree.getDepth()
cnt = 1
while cnt <= max_cnt:
tidy_drawing_tree(tree)
if tree.getDistanceBetweenSubtrees() == offset:
break
else:
cnt += 1
line 2~4
꽁냥이 아이디어의 1단계를 수행하는 곳입니다. 즉, 노드의 층 정보와 Traverse In Order를 이용하여 x, y 좌표를 부여합니다.
line 6~41
가장 핵심이 되는 코드입니다. 먼저 나무의 뿌리 노드를 가져옵니다(line 7). 만약 이 노드가 끝 마디(Leaf Node)인 경우에는 아무것도 수행하지 않습니다. 끝 마디가 아니라면 뿌리 노드를 자식 노드와 분리시키고(line 11~12) 각 자식 노드를 뿌리 노드로 하는 왼쪽, 오른쪽 서브 트리를 만들어줍니다(line 13~16).
다음으로 2단계를 수행하는데요. 양쪽 서브 트리 깊이가 같거나 오른쪽 서브 트리의 깊이가 더 얕으면 기준 층을 오른쪽 서브 트리의 깊이로 설정하고 아닌 경우에는 왼쪽 서브 트리의 깊이를 기준 층으로 합니다(line 18~24). 그러고 나서 해당 층에 대하여 왼쪽 서브 트리에서 가장 오른쪽, 오른쪽 서브 트리에서 가장 왼쪽에 있는 노드를 가져옵니다(line 26~27). 여기서 가져온 두 노드의 x 좌표 차이를 계산하고 최소 거리(offset)를 만족하기 위해 이동해야 하는 거리(shift)를 계산합니다(line 28~29). 그리고 왼쪽 서브 트리와 오른쪽 서브 트리를 이동해야 하는 거리의 절반만큼 옮겨줍니다(line 30~31). 이러한 작업을 왼쪽 서브 트리와 오른쪽 서브 트리에 대하여 수행합니다(line 33~34).
이제 3단계입니다. 뿌리 노드를 자식 노드의 중앙에 위치시키고(line 36) 자식 노드와 합쳐줍니다(line 38~41).
line 43~50
2~3 단계를 모든 왼쪽 서브 트리와 오른쪽 서브 트리가 최소 거리가 될 때까지 반복합니다. 이때 반복 횟수는 주어진 나무의 깊이로 설정하였습니다.
2.4 테스트
이제 테스트를 해볼 시간이에요. 아래 코드를 실행해보세요. 꽁냥이는 최소 거리를 2로 설정했습니다.
drawing_binary_tree(tree, offset=2)
이제 이를 산점도로 그려보겠습니다.
fig = plt.figure(figsize=(8,8))
fig.set_facecolor('white')
x_coords = []
y_coords = []
for nd in tree.traverseInOrder():
x_coords.append(nd.x)
y_coords.append(nd.y)
draw_connect_line(root)
plt.scatter(x_coords, y_coords, zorder=10)
plt.show()

앞서 살펴본 것과는 달리 뿌리 노드의 위치가 자식 노드의 중앙에 정확히 위치 된 것을 알 수 있습니다.
이제 마지막으로 노드에 포함된 텍스트를 표시해보겠습니다. 꽁냥이는 끝 마디는 하얀 박스로 설정하고 그 외에 마디는 각 층별로 같은 색이 되도록 트리를 그려주는 함수를 만들었습니다.
colors = sns.color_palette('hls', tree.getDepth()-1)
def drawNode(node, ax):
if node is not None:
if node.isLeaf:
bbox=dict(boxstyle='round',fc='white')
else:
bbox=dict(boxstyle='square',fc=colors[node.getLevel()-1], pad=1)
## 텍스트 표시
ax.text(node.x,node.y,node.text,bbox=bbox,fontsize=20,ha='center',va='center')
if node.parentNode is not None: ## 부모 노드와 자식 노드 연결
ax.plot((node.parentNode.x, node.x), (node.parentNode.y, node.y),color='k')
drawNode(node.leftChild, ax)
drawNode(node.rightChild, ax)
이제 나무를 그려볼까요? 아래 코드를 실행해보세요.
fig = plt.figure(figsize=(20,10))
renderer = fig.canvas.get_renderer()
ax = fig.add_subplot()
drawNode(root, ax)
x_coords = []
y_coords = []
for nd in tree.traverseInOrder():
x_coords.append(nd.x)
y_coords.append(nd.y)
min_x, max_x = min(x_coords), max(x_coords)
min_y, max_y = min(y_coords), max(y_coords)
## 캔버스 안에 나무가 표시되도록 x,y 축 상한 하한 설정
ax.set_xlim(min_x-1,max_x+1)
ax.set_ylim(min_y-0.5,max_y+0.5)
## 축은 안보이게 설정
ax.axes.xaxis.set_visible(False)
ax.axes.yaxis.set_visible(False)
이진 트리가 텍스트 정보를 포함하여 멋지게 그려지는 것을 확인할 수 있습니다. 참고로 여기서는 박스 폭에 대해서는 고려하지 않았습니다. 만약 인접한 노드들의 텍스트 박스가 겹친다면 이를 보정해줘야하지요.
이번 포스팅에서는 Matplotlib을 이용하여 이진 트리를 그려보는 방법에 대해서 알아보았습니다. 꽁냥이가 소개한 방법이 모든 트리에 대해서 실험해본 것이 아니라서 깊이가 깊은 나무에 대해서는 잘 그려질지 확신할 수는 없지만 그래도 웬만한 나무에 대해서는 잘 그려지는 것 같아요. 이번 기회를 통해서 나무를 시각화하는 알고리즘이 정말 많다는 것을 처음 알았어요. 꽁냥이는 그중에서 E M. Reingold, J S. Tilford이 소개한 Tidier Drawings of Trees 알고리즘이 가장 맘에 들었는데요. 이 논문을 봤는데 이해가 잘 안돼서 슬프네요.. 나중에 기회가 된다면 완벽하게 이해해보고 Matplotlib으로 구현해보는 것을 포스팅해볼게요. 지금까지 꽁냥이의 글 읽어주셔서 감사합니다.

참고자료
E M. Reingold, J S. Tilford - Tidier Drawings of Trees
Drawing Presentable Trees - http://llimllib.github.io/pymag-trees/
'데이터 분석 > 시각화' 카테고리의 다른 글
| Matplotlib 산포도에 히스토그램 추가하기 (817) | 2021.07.16 |
|---|---|
| Matplotlib 서로 다른 y축 적용하기 (1044) | 2021.07.13 |
| Matplotlib 메인 눈금(Major Tick) 서브 눈금(Minor Tick) 사용하기 (853) | 2021.06.14 |
| [Matplotlib Tip] 2. numpy.histogram을 이용하여 히스토그램 그리기 (1115) | 2021.06.12 |
| [Matplotlib Tip] 2. 산점도에 회귀 직선(곡선) 포함시키기 (1113) | 2021.05.28 |





댓글