Support Vector Machine의 아이디어를 어떻게 회귀 문제에 적용하는지 궁금해서 읽어본 자료이다. 이번 포스팅에서는 이를 공부한 내용을 정리한다.
- 목차 -
본 포스팅에서는 수식을 포함하고 있습니다.
티스토리 피드에서는 수식이 제대로 표시되지 않을 수 있으니
PC 웹 브라우저 또는 모바일 웹 브라우저에서 보시기 바랍니다.
1. Introduction
이 글의 목적은 서포트 벡터 회귀(Support Vector Regression : SVR)에 대해서 소개하고 이 분야의 최근 발전에 대한 개요를 알려주는 것이다.
1.1 Historic Background
SV(Support Vector) 알고리즘은 Generalized Portrait 알고리즘의 비선형 일반화 버전이며 VC(Vapnik and Chernovenkis) 이론에 근거하고 있다.
그리고 SV 분류기는 문자 인식, 사물 인식 등 여러 방면에서 좋은 성과를 내고 있다. 물론 SV는 회귀 문제에서도 놀라운 성과를 보여주었다.
1.2 The Basic Idea
학습데이터 (xi,yi),i=1,…,n이 있다고 하자. xi∈X,yi∈R이다. Vapnik이 1995년에 제안한 ϵ-SV에서의 목표는 모든 학습 데이터에 대하여 잔차가 기껏해야 ϵ인 함수 f중에선 최대한 평평한 평면을 찾는다. f의 형태는 다음과 같다.
f(x)=<w,x>+b,w∈X,b∈R
평평하다는 의미는 ‖이 작다는 의미이다.
그렇다면 \epsilon-SV가 풀고자 하는 문제는 다음과 같다.
\begin{align} & \text{minimize } \frac{1}{2} \|w\|^2 \\ & \text{subject to} \begin{cases} y_i-<w, x_i>-b \leq \epsilon \\ <w, x_i>+b-y_i\leq \epsilon \end{cases}\end{align}\tag{2}
하지만 (2)의 제약조건은 현실성이 없다. 특정 데이터는 정해진 \epsilon을 초과할 수 있기 때문이다. 따라서 이를 반영하기 위한 "soft margin" 손실 함수를 도입하였다. 이때에는 \xi_i, \xi_i^*를 도입하여 (2)를 다음과 같이 변형한다.
\begin{align} & \text{minimize } \frac{1}{2} \|w\|^2 + C\sum_{i=1}^n(\xi_i+\xi_i^*) \\ & \text{subject to} \begin{cases} y_i-<w, x_i>-b \leq \epsilon + \xi \\ <w, x_i>+b-y_i\leq \epsilon +\xi_i^* \\ \xi_i, \xi_i^i \geq 0 \end{cases}\end{align}\tag{3}
여기서 C는 f의 평평한 정도와 \epsilon을 초과하는 데이터에 대한 벌점을 주는 정도를 결정한다. 아래 그림에서 \xi에 대한 의미를 알 수 있다.

(3)은 이에 대응하는 듀얼 문제로 쉽게 풀 수 있다고 한다.
1.3 Dual Problem and Quadratic Programs
문제 (3)을 Lagrange 함수로 바꿔보면 아래와 같다.
L = \frac{1}{2}\|w\|^2+C\sum_{i=1}^n(\xi_i+\xi_i^*)-\sum_{i=1}^n(\eta_i\xi_i+\eta_i^*\xi_i^*)\\-\sum_{i=1}^n\alpha_i(\epsilon+\xi_i-y_i+<w,x_i>+b)\\-\sum_{i=1}^n\alpha_i^*(\epsilon+\xi_i+y_i-<w,x_i>-b) \tag{5}
이때 Lagrangian Multiplier \alpha_i^{(*)}, \eta_i^{(*)}는 모두 음이 아닌 실수이다. 이때 \alpha_i^{(*)}는 \alpha_i, \alpha_i^{*}를 의미한다.
Lagrange 함수에 대한 최적 조건(미분하면 0이 되는 그런 조건)을 이용하여 문제 (3)의 듀얼 문제를 재정의한다. 재정의를 하면 SV 알고리즘은 인풋 벡터의 내적으로 표현된다. SV 알고리즘을 통해 얻은 함수의 복잡도는 입력값의 차원이 아닌 SV의 개수의 의존한다고 한다. 또한 f(x)를 구할 때 듀얼 문제를 이용하면 w값을 알 필요가 없다. 이러한 편의성 덕분에 SVR을 비선형으로 쉽게 확장시킬 수 있다.
1.4 Computing b
절편항 b를 계산하는 방법을 소개한다. KKT 조건을 이용하거나 Interior Point Optimization를 이용하면 계산할 수 있다고 한다.
또한 w를 계산하기 위해서 모든 데이터가 필요한 것은 아니라고 한다. 이때 w를 계산하기 위해 필요한 인풋 벡터를 서포트 벡터라고 한다.
2. Kernels
2.1 Nonliearity by Preprocessing
지금까지는 함수 f가 인풋 벡터 x에 대하여 선형이었다. 실제 f가 복잡한 구조로 되어있다면 선형만으로 한계가 있어서 이를 비선형으로 확장해야 한다. 따라서 SV 알고리즘으로 비선형 함수를 잘 근사 시킬 수 있어야 한다. 여기에서는 커널을 이용하여 SV 알고리즘으로 비선형 함수를 추정하는 방법을 알아본다.
Example 1
다음과 같은 맵 \Phi : \mathbb{R}^2 \rightarrow \mathbb{R}^3이 있다고 해보자.
\Phi(x_1, x_2) = (x_1^2, \sqrt{2}x_1x_2, x_2^2)
이러한 맵을 이용하여 인풋 벡터를 전 처리한다면 SV 알고리즘이 만들어내는 f는 이차함수가 될 것이다. 하지만 이러한 맵핑은 인풋 벡터의 차원 d와 f의 다항 계수(이차함수면 2, 삼차 함수면 3 등) p가 커질수록 계산량이 많아진다. 정확히 계산하면 \begin{pmatrix} d+p-1 \\ p \end{pmatrix}이다. 실제로 Optical 문자 인식에서 좋은 성과를 보였던 SV 알고리즘은 p=7, d=28\cdot 28=784로 이는 대략적으로 3.7\cdot 10^{16}개의 피처를 갖게 된다.
2.2 Implicit Mappting via Kernels
그렇다면 복잡한 함수를 표현할 수 있지만 이러한 계산량 문제는 피할 수 없는 것일까? 아니다 커널이 그 답이다. 커널을 이용하면 계산량은 현저히 줄어들면서 복잡한 f를 만들어낼 수 있는 것이 커널의 핵심이다.
2.3 Conditions for Kernels
"그렇다면 커널 함수는 어떤걸 써야할까?"와 같은 질문을 하게 된다. 즉 "어떤 피처 공간에서의 내적에 대응하는 커널이 무엇인가? "말이다. 이 자료에서는 이에 대한 질문을 하는 정리를 소개한다.
특히 커널함수 k는 전이 불변성을 만족해야 한다. 이 섹션에서는 전이 불변성을 위한 필요충분조건을 소개한다.
2.4 Examples
여기에서는 몇몇 커널 함수의 예를 소개한다.
3. Cost Functions
여기서 고려하는 함수 f는 선형 함수이다. 하지만 커널을 이용하면 비선형 케이스에 대해서도 쉽게 확장 가능하다.
3.1 The Risk Functional
먼저 학습 데이터가 독립이고 동일한 분포로부터 나왔다고 해보자. 이때의 분포를 P(x, y)라 하자. 우리의 목표는 아래의 기대 위험을 최소화하는 것이다.
R(f) = \int c(x, y, f(x))dP(x,y)\tag{33}
c(x, y, f(x))는 주어진 데이터에 대하여 에러에 대하여 벌점을 주는 비용 함수이다. 하지만 P(x, y)를 모르기 때문에 경험 위험을 최소화하는 f를 찾게 된다.
R_{emp}(f) = \frac{1}{n}\sum_{i=1}^nc(x_i, y_i, f(x_i))
하지만 경험 위험을 최소화하는 것은 f의 클래스가 너무 커서 찾기 어렵다. 설사 찾는다 하더라도 과적합 가능성이 농후하다.
이러한 클래스의 크기를 조절하기 위하여 \|w\|^2에 대한 벌점항을 도입한다. 그래서 우리는 다음과 같은 새로운 경험 함수를 최소화하는 f를 찾게 된다.
R_{reg}(f) = R_{emp}(f)+\frac{\lambda}{2}\|w\|^2, \lambda>0\tag{35}
내용
3.2 Maximum Likelihood and Density Models
먼저 여러 가지 비용 함수를 소개하고 어떤 비용함수를 사용할지에 대한 질문을 던진다. 소개된 비용함수는 최적화시 굉장히 복잡해질 수 있다고 한다. 따라서 문제를 풀기 쉬운 비용함수를 소개하려고 한다.
먼저 샘플이 특정 함수와 에러를 더해서 생성되었다는 가정을 한다. 즉,
y_i = f_{true}(x_i) + \xi_i, \text{ with density } p(\xi)
이 경우 최적 비용 함수는 다음과 같다고 한다.
c(x, y, f(x)) = -\log p(y-f(x))
하지만 이러한 비용 함수는 non-Convex 문제가 될 수 있다고 한다. 이때에는 Convex 근사 함수를 도입하여 이를 비용함수로 대체하는 방법이 있을 수 있다.
보통 비용함수 c에 대하여 f(x)에 대해서 Convex라는 가정을 하게 된다. 이는 SV 알고리즘을 이용한 해가 유니크하게 존재하는 것을 보장하기 위해서이다.
마지막으로 여러 비용 함수와 확률 밀도 함수에 대해서 테이블 형식으로 소개한다.
3.3 Solving the Equations
문제의 단순화를 위하여 여기서 고려하는 비용 함수는 대칭이고 1차 미분이 \pm \epsilon에서 불연속이며 구간 [-\epsilon, \epsilon]에서는 0이라고 가정한다. 그리고 Primal 문제와 그의 듀얼 문제를 다시 정의한다.
3.4 Examples
여기서는 특정 비용 함수에 대하여 3.3에서 소개한 문제를 풀기 위한 여러 조건을 소개한다.
4. The Bigger Picture
먼저 SV 알고리즘을 도식화하면 아래와 같다.
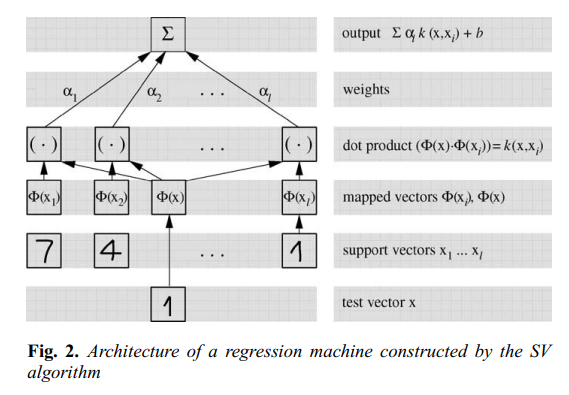
먼저 입력값 x가 들어오면 맵 \Phi에 의해서 변환되고 학습 데이터를 \Phi에 의해 변환시킨 것과 내적을 계산한다. 이는 커널을 계산하는 것과 같다. 다음으로 가중치를 곱해서 합해주고 마지막에 절편항 b를 더하면 최종 출력값을 얻게 된다.
아래 그림은 SV 알고리즘이 평평한 함수를 선택하는 것을 보여준다. 비록 평평하다는 것이 입력 공간(Input Space)이 아닌 \Phi에 의한 피처 공간(Feature Space)에 속하는 말이지만 사실 정규화 과정에 의하여 입력 공간에 대해서도 평평하다고 한다. 이는 정규화에 의한 커널의 평평한 성질에 기인한다.
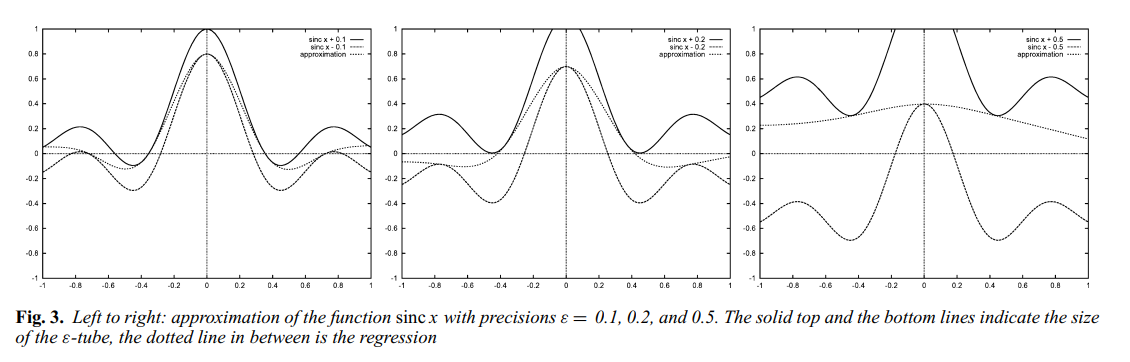
그리고 아래 그림은 근사 정확도와 성김성(Sparcity)의 관계를 보여준다.
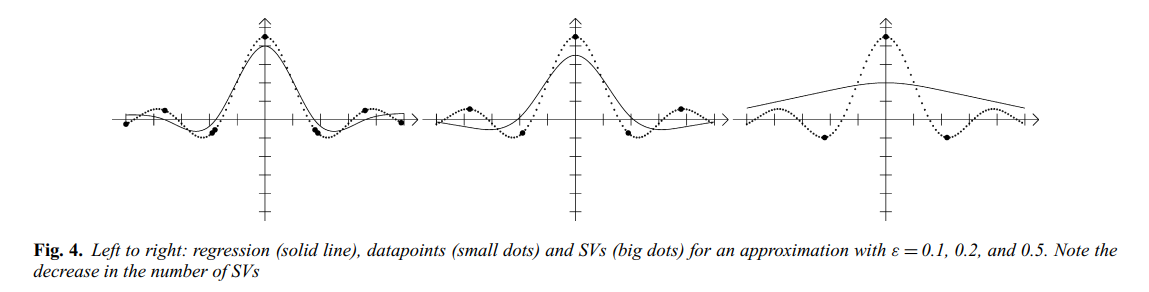
\epsilon이 커질수록(정확도가 낮아질수록) 실제 회귀 모형을 만드는데 필요한 SV(서포트 벡터) 개수는 줄어든다. 즉, 회귀 문제를 푸는 데 있어서 모든 데이터가 필요하지 않고 SV만 있으면 정확하게 같은 함수를 만들어낸다. 이는 데이터 압축 효과가 있다는 것이다. 하지만 이는 고차원 데이터나 노이즈가 존재하는 경우에는 그런 효과가 없을 수 있다고 한다.
5. Optimization Algorithms
지난 세월 동안 SV를 구현한 패키지는 엄청 많았지만 이 자료 저자는 몇 개의 구현 패키지만을 집중한다. 이러한 패키지는 가장 효율적이며 SV를 직접 구현하려는 사람에게 매우 유용할 것이라고 한다.
5.1 Implementations
대부분의 Quadratic Programming을 위한 상업용 패키지는 매우 안정적이라고 한다.
다음으로 여러 가지 패키지에 대한 내용을 소개한다. 근데 관심 없어서 생략(왜 파이썬에 대한 내용은 없는 걸까?=>이 자료가 2004년에 만들어졌다는 걸 잊고 있었다).
5.2 Basic Notions
SV 알고리즘은 컨벡스 최적화에서 듀얼 이론에 많이 의존한다. 여기서는 편의성을 위하여 몇 가지 관련 내용을 증명 없이 소개한다.
Uniqueness
모든 컨벡스 제약 최적화 문제는 유일한 해를 가진다.
Lagrange Function
Lagrange Function(LF)은 프리말(Primal) 변수에 대하여 최소화함과 동시에 Lagrange Multiplier(듀얼 변수)에 대해서 최대화하게 된다.
Dual Objective Function
이는 LF를 프리말 변수에 대하여 최소화함으로써 얻어진다. 따라서 이는 듀얼 변수로 표현된다.
Duality Gap
프리말 목적함수는 항상 듀얼 목적함수보다 크거나 같으며 같지 않은 경우의 차이를 Duality Gap이라 한다.
KKT Condition
프리말 변수와 듀얼 변수들이 Feasible하고 KKT 조건은 만족하면 그것이 해가 된다.
5.3 Interior Point Algorithms
IPD(Interior Point Algorithms)은 듀얼 최적화 문제로 변환하고 프리말과 듀얼 문제를 동시에 풀게 된다. 이때 Feasible한 해를 찾거나 듀얼 갭을 계산하기 위하여 KKT 조건을 사용한다.
5.4 Useful Tricks
IPD의 아이디어를 이용하여 알고리즘을 유도하는데 영향을 줄 수 있는 몇 가지 트릭을 소개한다고 한다.
관심 없어서 생략
5.5 Subset Selection Algorithms
여기서 소개한 컨벡스 프로그래밍 알고리즘은 데이터가 한 3000개 까지는 잘 동작하지만 너무 많으면 컴퓨터 성능 제약으로 인하여 계산이 어렵다. 특히 커널 계산 시 조합의 수가 들어가므로 엄청 많아진다.
Vapnik은 전체 데이터가 아닌 SV만을 가지고 컴퓨터 메모리를 아끼면서 해를 만들어 낼 수 있다고 했다. 즉, 사전에 SV를 알 수 있다면 그렇게 할 수 있다는 것이다. 여기서는 SV를 사전에 알지 못해도 메모리를 아끼면서 해를 구하는 방법을 소개한다.
5.6 Sequential Minimal Optimization
SMO는 사이즈가 2인 부분집합을 이용하여 뭔가를 하는 거 같은데 잘 모르겠다. ㅠㅠ
6. Variations on a Theme
여기서는 기존 SV 알고리즘을 여러 상황에 적합한 수정 버전을 소개한다.
6.1 Convex Combination and l_1-Norms
이는 식 (35)의 마지막 항을 \alpha의 l_1-norm으로 바꾼 것이다.
6.2 Automatic Tuning of the Insensitivity Tube
여기서는 \epsilon을 어떻게 초이스 해야 하는지에 관한 내용이 나온다. 핵심은 (35)에 \epsilon과 관련된 항을 포함시켜 최적화를 시키면 자동적으로 최적 \epsilon이 구해진다고 한다. 다음과 같이 말이다.
R_v(f) = R_{emp}(f)+\frac{\lambda}{2}\|w\|^2+v\epsilon \tag{60}
(60)을 최소화하면 자동적으로 최적 \epsilon을 구해줄 뿐만 아니라 v가 SV의 개수에 대한 상한과 하한 정보를 제공한다고 한다.
7. Regularization
지금까지는 \Phi를 그냥 쓰기만 했지 이에 대한 성질에 대해선 관심이 없었다. 사실 커널을 쓰기 때문에 \Phi는 암묵적으로 사용되었지만 그 형태는 명확하지 않아서이다.
커널에 대한 심도 있는 이해는 적절한 커널을 선택하는데 도움이 된다. 또한 피처 맵 \Phi는 차원의 저주를 피할 수 있게 해준다고 한다.
7.1 Regularization Networks
SV 알고리즘과 Regularization Networks(RN)과의 관계를 알아보기 위하여 먼저 RN에 대한 개요를 소개한다.
7.2 Green's Functions
RN의 정규화 연산자와 SV에서 사용하는 커널 사이의 관계를 소개한다.
7.3 Translation Invariant Kernels
여기에서는 몇 가지 상황에 대해서 어떤 커널을 사용해야 하는가에 대한 내용을 소개한다.
7.4 Capacity Control
여기서는 하이퍼 파라미터를 어떻게 설정할 것인가에 대한 이야기가 나온다. Minimum Description Length를 이용한 방법, 베이지안 추정법 그리고 교차검증을 이용한 방법을 소개했다.
8. Conclusion
SV 알고리즘 분야는 굉장히 광범위하여 튜토리얼에 이 모든 것을 담을 수 없었다. 차라리 교재(Textbook)라면 모를까..
하지만 이 자료의 저자들은 너무 편향적이지 않고 SV 알고리즘에 대한 개요를 제공했다고 생각한다. 저자는 다음의 토픽을 고의로 생략했다고 한다.
8.1 Missing Topics
Mathematical Programming
애초에 다른 관점에서부터 시작된 거라서 생략한 거 같다. 관심 있는 사람들을 위한 참고 자료를 제공한다.
Density Estimation
SV 알고리즘을 이용하여 밀도 함수 추정이 가능한가 보다. 하지만 메인 주제는 아니어서 생략한 듯?
Dictionary
Wavelet 관련 내용인데 뭔 말인지 잘 모르겠다.
Application
애초의 이 자료의 목적이 방법론과 이론이어서 적용 부분은 신경 쓰지 않았다.
8.2 Open Issues
2000년대 초반에는 서포트 벡터 머신이 굉장히 핫한 주제였기 때문에 그에 따라 여러 오픈 이슈들이 있다. 특히 에러 바운드에 관한 것 말이다. 또한 사전 정보를 SV 알고리즘에 어떻게 녹여낼지에 대한 것도 향후 문제라고도 한다.

'통계 > 논문 리뷰' 카테고리의 다른 글
| Greedy Function Approximation : A Gradient Boosting Machine (386) | 2022.06.15 |
|---|---|
| Random Forests (419) | 2022.05.27 |
| Multi-class AdaBoost (396) | 2022.05.03 |
| A Method for Computing Profile-Likelihood-Based Confidence Intervals (390) | 2022.04.30 |
| [논문 리뷰] 6. Testing for A Unit Root in Time Series Regression (411) | 2022.04.17 |





댓글